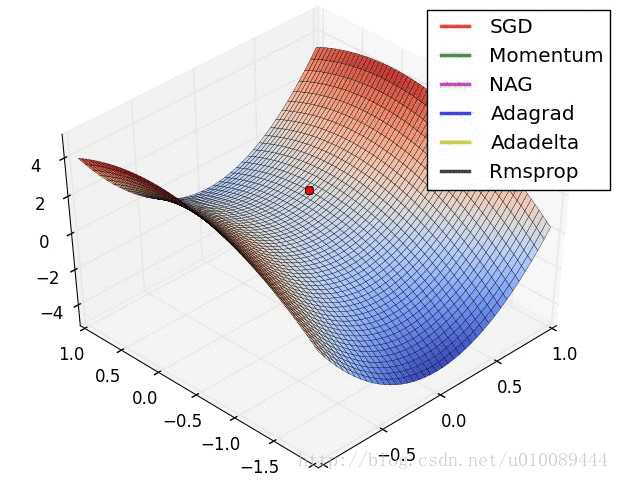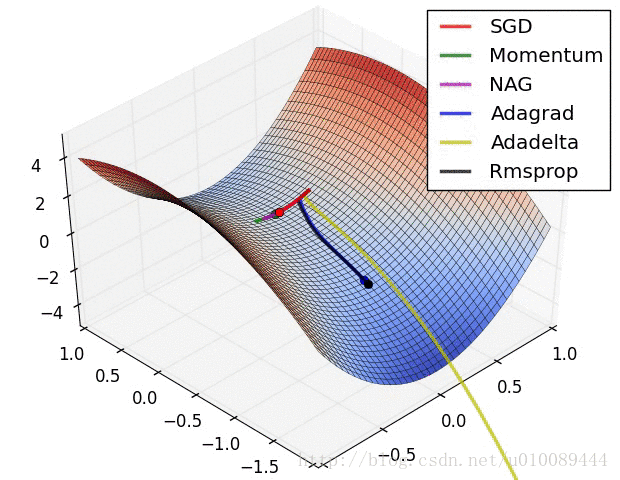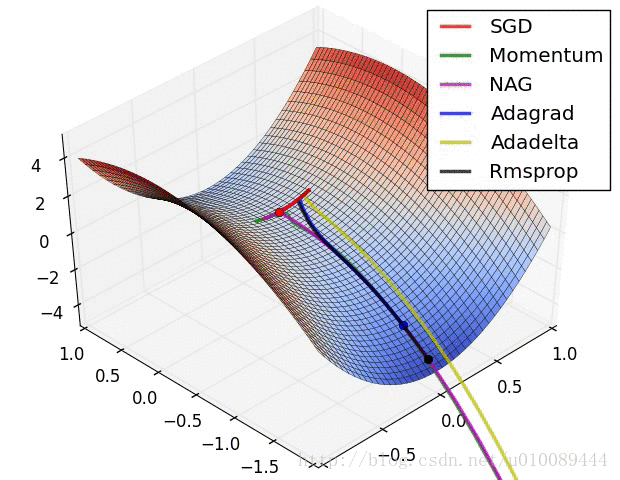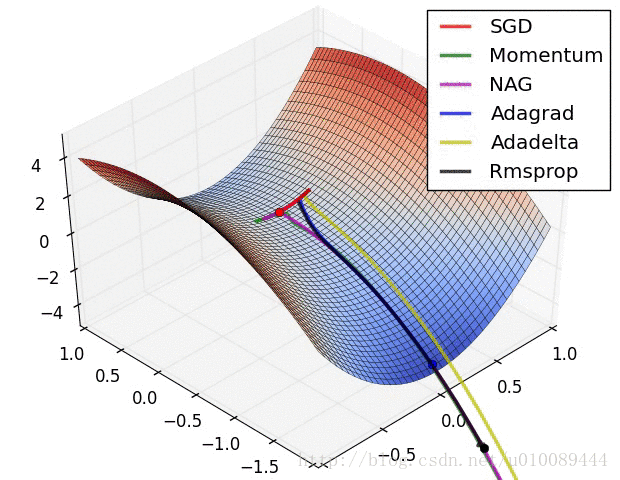
无约束局部解

$$minf(x), x \in R^n$$

• 若存在$x^{ } \in R^n, \epsilon > 0, \forall x \in R^n$ 使得$|x - x^{ }| < \epsilon$时，恒有
• $f(x) \geq f(x^{ })$：则称$x^{ }$为f(x)的 local minimum point/solution（局部极小点/局部解）
• $f(x) > f(x^{ })$：则称$x^{ }$为f(x)的 严格局部极小点/局部解

最优性条件

First-Order Necessary Condtion

• 无约束问题局部解的一阶必要条件：设f(x)有连续的一阶偏导， 弱$x^{ * }$是无约束问题的局部解，则 $$\triangledown f(x{* }) = 0$$

Second-Order Necessary Condition

• 无约束问题局部解的二阶必要条件：设f(x)有连续二阶偏导， 若$x^{ * }$是无约束问题的局部解，则

  • $$\triangledown f(x^{ * }) = 0$$
  • $$\triangledown^2 f(x^{ * })半正定$$

Second-Order Sufficient Condition

• 无约束问题局部解的二阶充分条件：设f(x)有连续二阶偏导， 若在$x^{ }$处满足以下，则x^{ }是无约束问题的 严格局部解

  • $$\triangledown f(x^{ * }) = 0$$
  • $$\triangledown^2 f(x^{ * })正定$$

下降算法

迭代算法：将当前迭代点向正确方向移动一定步长，然后 检验目标值是否满足一定要求

• 方向、步长就是不同优化算法主要关心的两个方面
• 还关心算法的rate of convergence（收敛速率）

一般下降算法框架

1. 取初始点$x^{(1)}$，置精度要求$\epsilon$，置k=1

2. 若在点$x^{(k)}$处满足某个终止准则，则停止计算，得无约束 优化问题最优解$x^{(k)}$，否则适当地选择$x^{(k)}$处 搜索方向

3. 进行适当的一维搜索，求解一维问题

   $$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$$

4. 置k=k+1，转2

要使下降算法可行，需要确定

• 某点出搜索方向
  • 负梯度方向
  • Newton方向：求方向的时候已确定步长，也可用做步长搜索
  • 拟Newton方向
• 求步长地一维搜索方式
  • 试探法
    • 0.618法
    • Fibonacci方法（分数法）
    • 二分法
  • 插值法
    • 三点二次插值法
    • 二点二次插值法
    • 两点三次插值法
  • 非精确一维搜索方法
    • Glodstein方法
    • Armijo方法
    • Wolfe-Powell方法

• 算法终止准则

  • $|\triangledown f(x^{(k)})| < \epsilon$
  • $|x^{(k+1)} - x^{(k)}| < \epsilon$
  • $|f(x^{(k+1)}) - f(x^{(k)})| < \epsilon$

  • 实际计算中最优解可能永远无法迭代达到，应该采用较弱 终止准则

算法收敛性

• 收敛：序列${x^{(k)}}$或其一个子列（仍记${x^{(k)}}$） 满足 $$\lim_{k \rightarrow \infty} x^{(k)} = x^{ * }$$

  • $x^{ * }$：无约束问题局部解

但是这样强的结果难以证明

• 往往只能证明${x^{(k)}}$的任一聚点的稳定点
• 或是更弱的 $$\lim_{k \rightarrow \infty} inf \|\triangledown f(x^{(k)}) \| = 0$$

• 局部收敛算法：只有初始点充分靠近极小点时，才能保证产生 序列收敛
• 全局收敛算法：对任意初始点，产生序列均能收敛

收敛速率

设序列${x^{(k)}}$收敛到$x^{ * }$，若以下极限存在

$$\lim _ {k \rightarrow \infty} \frac {\|x^{(k+1)} - x^{*}\|} {\|x^{(k)} - x^{*}\|} = \beta$$

• $0 < \beta < 1$：线性收敛
• $\beta = 0$：超线性收敛
• $\beta = 1$：次线性收敛（收敛速率太慢，一般不考虑）

算法的二次终止性

• 二次终止性：若某算法对任意正定二次函数，从任意初始点出发 ，都能经过有限步迭代达到其极小点，则称该算法有二次终止性

具有二次终止性的算法被认为时好算法，否则计算效果较差，原因

• 正定二次目标函数有某些好的性质，好的算法应该能在有限步内 达到其极小点

• 对于一个一般的目标函数，若其在极小点处的Hesse矩阵 $\triangledown f(x^{( * )})$，则由泰勒展开式得到

  $$\begin{align*} f(x) & = f(x^{*}) + \triangledown f(x^ {*})^T(x - x^{*}) \\ & + \frac 1 2 (x - x^{*})^T \triangledown^2 f(x^{*}) (x - x^{*}) \\ & + o(\|x - x^{*}\|^2) \end{align*}$$

  即目标函数f(x)在极小点附近与一个正定二次函数近似，所以对 正定二次函数好的算法，对一般目标函数也应该具有较好的性质

Linear Programming

数学模型

一般数学模型

线性规划问题（LP）可以抽象为一般的数学模型

$$\begin{array}{l} (\min_x, \max_x) & S=c_1 x_1 + c_2 x_2 + \cdots + c_n x_n \\ s.t. & \left \{ \begin{array} {l} a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n (\geq = \leq) b_1 \\ a_{2,1} x_1 + a_{2,2} x_2 + \cdots + a_{2,n} x_n (\geq = \leq) b_2 \\ \vdots \\ a_{m,1} x_1 + a_{m,2} x_2 + \cdots + a_{m,n} x_n (\geq = \leq) b_m \end{array} \right. \end{array}$$

• $S = c_1 x_1 + c_2 x_2 + \cdots + c_n x_n$：目标函数
• $x_1, x_2, …, x_n$：待求解变量
• $bi、c_i、a{ij}$：实常数
• $(\geq = \leq)$：在三种符号中取一种

标准形式

$$\begin{array}{l} \min_x & S=c_1 x_1 + c_2 x_2 + \cdots + c_n x_n \\ s.t. & a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n = b_1 \\ & \vdots \\ & a_{t,1} x_1 + a_{t,2} x_2 + \cdots + a_{t,n} x_n = b_t \\ & a_{t+1,1} x_1 + a_{t+1,2} x_2 + \cdots + a_{t+1, n} x_n \leq b_{t+1} \\ & \vdots \\ & a_{t+l,1} x_1 + a_{t+l,2} x_2 + \cdots + a_{t+l, n} x_n \leq b_{t+l} \\ \end{array}$$

• $\max_x$：目标函数取翻转换为$\min_x$

• $\geq$：不等式左右取反转换为$\leq$

• 线性规划一般模式都可以等价转换为标准形式

Simplex Method

单纯型法：利用线性规划极值点必然在单纯型顶点取得，不断迭代顶点求出极值

算法

• 初始化：标准化线性规划问题，建立初始表格
  • 最小化目标函数：目标函数系数取反，求极大
  • 不等式约束：加入松弛变量（代表不等式两端差值）
  • 变量非负：定义为两个非负变量之差
• 最优测试
  • 若目标行系数都为非负，得到最优解，迭代停止
  • 基变量解在右端列中，非基变量解为 0
• 确定主元列
  • 从目标行的前 $n$ 个单元格中选择一个非负单元格，确定主元列
  • 选择首个非负：解稳定，若存在最优解总是能取到
  • 选择绝对值最大：目标函数下降快，但有可能陷入死循环，无法得到最优解（不满足最优条件）

• 确定主元（分离变量）（行）

  • 对主元列所有正系数，计算右端项和其比值 $\Theta$ 比率
  • 最小 $\Theta$ 比率确定主元（行）（类似的为避免死循环，总是选择首个最小者）

• 转轴变换（建立新单纯形表）

  • 主元变 1：主元行所有变量除以主元
  • 主元列变 0：其余行减去其主元列倍主元行
  • 交换基变量：主元行变量标记为主元列对应变量

特点

• 算法时间效率
  • 极点规模随着问题规模指数增长，所以最差效率是指数级
  • 实际应用表明，对 $m$ 个约束、$n$ 个变量的问题，算法迭代次数在 $m$ 到 $3m$ 之间，每次迭代次数正比于 $nm$
• 迭代改进

Two-Phase Simplex Method

两阶段单纯形法：单纯型表中没有单元矩阵，无法方便找到基本可行解时使用

• 在给定问题的约束等式中加入人工变量，使得新问题具有明显可行解
• 利用单纯形法求解最小化新的线性规划问题

其他一些算法

• 大 M 算法
• Ellipsoid Method 椭球算法
  • 算法时间效率
    • 可以在多项式时间内对任意线性规划问题求解
    • 实际应用效果较单纯形法差，但是最差效率更好
• Karmarkar 算法
  • 内点法（迭代改进）

凸优化

$$\begin{array}{l} \min_x & f(x) \\ s.t. & g_i(x) \leq 0, i=1，2,\cdots,k \\ & h_i(x) = 0, i=1,2,\cdots,l \end{array}$$

• $f(x), g(x)$：$R^n$ 上连续可微的凸函数
• $h_i(x)$：$R^n$ 上仿射函数
• 仿射函数：满足 $f(x)=ax+b, a \in R^n, b \in R, x \in R^n$

二次规划

$$\begin{array}{l} \min_x & f(x)=\frac 1 2 x^TGx + c^Tx \\ s.t. & Ax \leq b \end{array}$$

• $G \in R^{n * n}$：$n$ 阶实对称矩阵
• $A \in R^{m n}$：$m n$ 实矩阵
• $b \in R^m$
• $c \in R^n$

• $G$ 正定

  • 此时目标函数 $f(x)$ 为凸函数
  • 凸二次规划
  • 问题有唯一全局最小值
  • 问题可可由椭球法在多项式时间内求解

• $G$ 半正定

  • 此时目标函数 $f(x)$ 为凸函数
  • 半定规划
  • 若约束条件可行域不空，且目标函数在此可行域有下界，则问题有全局最小值

• $G$非正定

  • 目标函数有多个平稳点（局部极小），NP-hard 问题

求解

• 椭球法
• 内点法
• 增广拉格朗日法
• 投影梯度法

二阶锥规划

$$\begin{array}{l} \min_x & f^Tx \\ s.t. & \|A_ix + b_i \|_2 \leq c_i^Tx + d_i, i=1,2,\cdots,m \\ & Bx=g \end{array}$$

• $f \in R^n$
• $A_i \in R^{n_i * n}$，$b_i \in R^{n_i}$，$c_i \in R^{n_i}$，$d_i \in R$
• $B \in R^{p * n}$，$g \in R^n$

• $A_i=0,i=1,\cdots,m$：退化为线性规划

• 一般的二阶规划可以转换为二阶锥规划

  $$X^TAX + qTX + C \leq 0 \Rightarrow \|A^{1/2}x + \frac 1 2 A^{-1/2}q\|^{1/2} \leq -\frac 1 4 q^TA^{-1}q - c$$

• 二阶锥规划可以使用内点法很快求解（多项式时间）

非线性最小二乘

$$\begin{align*} f(x) & = \frac 1 2 \sum_{i=1}^m r^2_i(x) \\ & = \frac 1 2 r(x) r^T(x) \end{align*}$$

• $r_i(x)$：通常为非线性函数
• $r(x) = (r_1(x), \cdots, r_n(x))^T$
• $x \in R^n, m \geq n$

• 考虑目标函数梯度、Hesse 矩阵

  $$\begin{align*} \nabla f(x) & = \sum_{i=1}^m \nabla r_i(x) r_i(x) \\ & = J(x)^T r(x) \\ \nabla^2 f(x) & = \sum_{i=1}^m \nabla r_i(x) r_i(x) + \sum_{i=1}^m r_i \nabla^2 r_i(x) \\ & = J(x)^T J(x) + \sum_{i=1}^m r_i(x) \nabla^2 r_i(x) \end{align*}$$

• $$J(x) = \begin{bmatrix} \frac {\partial r_1} {\partial x_1} & \frac {\partial r_1} {\partial x_2} & \cdots & \frac {\partial r_1} {\partial x_n} \\ \frac {\partial r_2} {\partial x_1} & \frac {\partial r_2} {\partial x_2} & \cdots & \frac {\partial r_2} {\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial r_m} {\partial x_1} & \frac {\partial r_m} {\partial x_2} & \cdots & \frac {\partial r_m} {\partial x_n} \end{bmatrix} = \begin{bmatrix} \nabla r_1(x)^T \\ \nabla r_2(x)^T \\ \vdots \\ \nabla r_m(x)^T \\ \end{bmatrix}$$ 为$r(x)$的 Jacobi 矩阵

Gauss-Newton 法

• 为简化计算，略去 Newton 法中 Hesse 矩阵中 $\sum_{i=1}^m r_i(x) \nabla^2 r_i(x)$ 项，即直接求解方程组

  $$J(x^{(k)})^T J(x^{(k)}) d = -J(x^{(k)})^T r(x^{(k)})$$

• 求解同一般 Newton 法

特点

• 实际问题中

  • 局部解 $x^{ }$ 对应的目标函数值 $f(x^{ })$ 接近 0 时，采用 Gauss-Newton 法效果较好，此时
    • $|r(x^{(k)})|$ 较小
    • 曲线$r_i(x)$接近直线
    • $\nabla^2 r_i(x) \approx 0$
  • 否则效果一般

• 矩阵 $J(x^{(k)})^T J(x^{(k)})$ 是半正定矩阵

  • 当 Jacobi 矩阵列满秩时为正定矩阵，此时虽然 $d^{(k)}$ 是下降方向，但仍需类似修正牛顿法增加一维搜索策略保证目标函数值不上升

Levenberg-Marquardt 方法

• 考虑到 $J(x^{(k)})$ 中各列线性相关、接近线性相关，求解 Newton-Gauss 方法中的方程组会出现困难，可以改为求解

  $$(J(x^{(k)})^T J(x^{(k)}) + vI) d = -J(x^{(k)})^T r(x^{(k)})$$

• $v$：迭代过程中需要调整的参数，LM 方法的关键即如何调整

定理1

• 若 $d(v)$ 是以上方程组的解，则 $|d(v)|^2$ 是 $v$ 的连续下降函数，且 $v \rightarrow +\infty, |d(v)| \rightarrow 0$

• $J(x^{(k)})^T J(x^{(k)})$ 是对称半正定矩阵，则存在正交阵

  $$(P^{(k)})^T J(x^{(k)})^T J(x^{(k)}) P^{(k)} = \Lambda^{(k)}$$

• 则可以解出 $|d(v)|^2$

• 增大 $v$ 可以限制 $|d^{(k)}|$，所以 LM 方法也被称为阻尼最小二乘法

定理2

• 若 $d(v)$ 是以上方程的解，则 $d(v)$ 是 $f(x)$ 在 $x^{(k)}$ 处的下降方向，且 $v \rightarrow + \infty$ 时，$d(v)$ 的方向与 $-J(x^{(k)})^T r(x^{(k)})$ 方向一致

• 下降方向：$\nabla f(x^{(k)}) d(v) < 0$ 即可
• 方向一致：夹角余弦

• $v$充分大时，LM 方法产生的搜索方向 $d^{(k)}$ 和负梯度方向一致

参数调整方法

• 使用梯度、近似 Hesse 矩阵定义二次函数 $$q(d) = f(x^{(k)}) + (J(x^{(k)})^T r(x^{(k)}))^T d + \frac 1 2 d^T (J(x^{(k)})^T J(x^{(k)})) d$$

• 其增量为

  $$\begin{align*} \Delta q^{(k)} & = q(d^{(k)}) - q(0) \\ & = (J(x^{(k)})^T r(x^{(k)}))^T d^{(k)} + \frac 1 2 (d^{(k)})^T (J(x^{(k)})^T J(x^{(k)})) d^{(k)} \end{align*}$$

• 目标函数增量

  $$\begin{align*} \Delta f^{(k)} & = f(x^{(k)} + d^{(k)}) - f(x^{(k)}) \\ & = f(x^{(k+1)}) - f(x^{(k)}) \end{align*}$$

• 定义$\gamma_k = \frac {\Delta f^{(k)}} {\Delta q^{(k)}}$

  • $\gamma_k$接近1说明$\Delta f^{(k)}$接近$\Delta q^{(k)}$

    • 即$f(x^{(k)} + d^{(k+1)})$接近$q(d^{(k)})$
    • 即$f(x)$在$x^{(k)}$附近接近二次函数
    • 即使用Gauss-Newton方法求解最小二乘问题效果较好
    • 即LM方法求解时$v$参数应该较小

  • $\gamma_k$接近0说明$\Delta f^{(k)}$与$\Delta q^{(k)}$ 近似程度不好

    • $d^{(k)}$不应取得过大，应减少$d^{(k)}$得模长
    • 应该增加参数$v$进行限制
    • 迭代方向趋近于负梯度方向

  • $\gamma_k$适中时，认为参数$v$选取合适，不做调整

    • 临界值通常为0.25、0.75

算法

1. 初始点 $x^{(1)}$、初始参数 $v$（小值）、精度要求 $\epsilon$，置 $k=k+1$

2. 若 $|J(x^{(k)})^T r(x^{(k)})| < \epsilon$，则停止计算，得到问题解 $x^{(k)}$，否则求解线性方程组

   $$(J(x^{(k)})^T J(x^{(k)}) + v_kI) d = -J(x^{(k)})^T r(x^{(k)})$$

   得到 $d^{(k)}$

3. 置 $x^{(k+1)} = x^{(k)} + d^{(k)}$，计算 $\gamma_k$

4. 考虑 $\gamma$

   • $\gamma < 0.25$，置$v_{k+1} = 4 v_k$
   • $\gamma > 0.75$，置$v_{k+1} = v_k / 2$
   • 否则置$v_{k+1} = v_k$

5. 置k=k+1，转2

其他问题

整形规划

整形规划：求线性函数的最值，函数包含若干整数变量，并且满足线性等式、不等式的有限约束

Unregularized Least Squares Learning Problem

$$w_T = \frac \gamma n \sum_{i=0}^{T-1} (I - \frac \gamma n {\hat X}^T \hat X)^i {\hat X}^T \hat Y$$

• $\gamma$：被引入保证 $|I - \frac \gamma n {\hat X}^T \hat X| < 1$

策略

• 考虑

  $$\min_w I_s(w) = \frac 1 {2n} \|\hat X w - \hat Y\|^2$$

• 将$w_{t+1}$带入$I_s(w)$即可证明每次迭代$I_s(w)$减小

  $$w_0 = 0 \\ w_{t+1} = (I - \frac \gamma n {\hat X}^T \hat X)w_t + \frac \gamma n {\hat X}^T \hat Y$$

正定二次目标函数

$$min f(x) = \frac 1 2 x^T G x + r^T x + \sigma$$

非线性最小二乘

$$\begin{align*} f(x) & = \frac 1 2 \sum_{i=1}^m r^2_i(x) \\ & = \frac 1 2 r(x) r^T(x) \end{align*}$$

• $r_i(x)$：通常为非线性函数
• $r(x) = (r_1(x), \cdots, r_n(x))^T$
• $x \in R^n, m \geq n$

则

$$\begin{align*} \nabla f(x) & = \sum_{i=1}^m \nabla r_i(x) r_i(x) \\ & = J(x)^T r(x) \\ \nabla^2 f(x) & = \sum_{i=1}^m \nabla r_i(x) r_i(x) + \sum_{i=1}^m r_i \nabla^2 r_i(x) \\ & = J(x)^T J(x) + \sum_{i=1}^m r_i(x) \nabla^2 r_i(x) \end{align*}$$

• $$J(x) = \begin{bmatrix} \frac {\partial r_1} {\partial x_1} & \frac {\partial r_1} {\partial x_2} & \cdots & \frac {\partial r_1} {\partial x_n} \\ \frac {\partial r_2} {\partial x_1} & \frac {\partial r_2} {\partial x_2} & \cdots & \frac {\partial r_2} {\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial r_m} {\partial x_1} & \frac {\partial r_m} {\partial x_2} & \cdots & \frac {\partial r_m} {\partial x_n} \end{bmatrix} = \begin{bmatrix} \nabla r_1(x)^T \\ \nabla r_2(x)^T \\ \vdots \\ \nabla r_m(x)^T \\ \end{bmatrix}$$ 为$r(x)$的Jacobi矩阵

Gauss-Newton法

Newton法中为简化计算，略去其Hesse矩阵中 $\sum_{i=1}^m r_i(x) \nabla^2 r_i(x)$项，即直接求解 方程组

$$J(x^{(k)})^T J(x^{(k)}) d = -J(x^{(k)})^T r(x^{(k)})$$

算法

同Newton法，仅求解Newton方程改为求解以上方程组

特点

• 实际问题中

  • 局部解$x^{ }$对应的目标函数值$f(x^{ })$接近0 时，$|r(x^{(k)})|$较小
  • 曲线$r_i(x)$接近直线， $\nabla^2 r_i(x) \approx 0$

  采用Gauss-Newton法效果较好，否则效果一般

• 矩阵$J(x^{(k)})^T J(x^{(k)})$是半正定矩阵，当Jacobi矩阵 列满秩时为正定矩阵，此时虽然$d^{(k)}$是下降方向，但仍需 类似修正牛顿法增加一维搜索策略保证目标函数值不上升

Levenberg-Marquardt方法

但$J(x^{(k)})$中各列线性相关、接近线性相关，则求解 Newton-Gauss方法中的方程组会出现困难，可以改为求解

$$(J(x^{(k)})^T J(x^{(k)}) + vI) d = -J(x^{(k)})^T r(x^{(k)})$$

• $v$：迭代过程中需要调整的参数，LM方法的关键即如何调整

定理1

• 若$d(v)$是以上方程组的解，则$|d(v)|^2$是$v$的连续下降 函数，且$v \rightarrow +\infty, |d(v)| \rightarrow 0$

• $J(x^{(k)})^T J(x^{(k)})$是对称半正定矩阵，则存在正交阵

  $$(P^{(k)})^T J(x^{(k)})^T J(x^{(k)}) P^{(k)} = \Lambda^{(k)}$$

• 则可以解出$|d(v)|^2$

• 增大$v$可以限制$|d^{(k)}|$，所以LM方法也被称为阻尼最小 二乘法

定理2

• 若$d(v)$是以上方程的解，则$d(v)$是$f(x)$在$x^{(k)}$处的 下降方向，且$v \rightarrow + \infty$时，$d(v)$的方向与 $-J(x^{(k)})^T r(x^{(k)})$方向一致

• 下降方向：$\nabla f(x^{(k)}) d(v) < 0$即可
• 方向一致：夹角余弦

• $v$充分大时，LM方法产生的搜索方向$d^{(k)}$和负梯度方向 一致

参数调整方法

使用梯度、近似Hesse矩阵定义二次函数

$$q(d) = f(x^{(k)}) + (J(x^{(k)})^T r(x^{(k)}))^T d + \frac 1 2 d^T (J(x^{(k)})^T J(x^{(k)})) d$$

• 其增量为

  $$\begin{align*} \Delta q^{(k)} & = q(d^{(k)}) - q(0) \\ & = (J(x^{(k)})^T r(x^{(k)}))^T d^{(k)} + \frac 1 2 (d^{(k)})^T (J(x^{(k)})^T J(x^{(k)})) d^{(k)} \end{align*}$$

• 目标函数增量

  $$\begin{align*} \Delta f^{(k)} & = f(x^{(k)} + d^{(k)}) - f(x^{(k)}) \\ & = f(x^{(k+1)}) - f(x^{(k)}) \end{align*}$$

• 定义$\gamma_k = \frac {\Delta f^{(k)}} {\Delta q^{(k)}}$

• $\gamma_k$接近1说明$\Delta f^{(k)}$接近$\Delta q^{(k)}$

  • 即$f(x^{(k)} + d^{(k+1)})$接近$q(d^{(k)})$
  • 即$f(x)$在$x^{(k)}$附近接近二次函数
  • 即使用Gauss-Newton方法求解最小二乘问题效果较好
  • 即LM方法求解时$v$参数应该较小

• $\gamma_k$接近0说明$\Delta f^{(k)}$与$\Delta q^{(k)}$ 近似程度不好

  • $d^{(k)}$不应取得过大，应减少$d^{(k)}$得模长
  • 应该增加参数$v$进行限制
  • 迭代方向趋近于负梯度方向

• $\gamma_k$适中时，认为参数$v$选取合适，不做调整

  • 临界值通常为0.25、0.75

算法

1. 初始点$x^{(1)}$、初始参数$v$（小值）、精度要求$\epsilon$ ，置k=k+1

2. 若$|J(x^{(k)})^T r(x^{(k)})| < \epsilon$，则停止计算， 得到问题解$x^{(k)}$，否则求解线性方程组

   $$(J(x^{(k)})^T J(x^{(k)}) + v_kI) d = -J(x^{(k)})^T r(x^{(k)})$$

   得到$d^{(k)}$

3. 置$x^{(k+1)} = x^{(k)} + d^{(k)}$，计算$\gamma_k$

4. 若

   • $\gamma < 0.25$，置$v_{k+1} = 4 v_k$
   • $\gamma > 0.75$，置$v_{k+1} = v_k / 2$
   • 否则置$v_{k+1} = v_k$

5. 置k=k+1，转2

Cone

• 锥：$C \subset V, \forall x \in C, a>0 \Rightarrow ax \in C$

  • 锥总是无界的

  • $V$：向量空间

• Convex Cone 凸锥：$\forall x,y \in C, \forall a,b > 0 \Rightarrow ax + by \in C$

  • 凸锥必然是凸集
  • 非凸锥：凸锥的补集

• Norm Cone $n$ 维标准锥：$C = { (x,t)| |x|_2 \leq t, x \in R^{n-1}, t \in R }$

• Second Order Cone 二阶锥：$C = { (x,t)|Ax+b|_2 \leq c^Tx + d }$

  • 二阶锥相对于对标准锥做了仿射变换（平移变换）

Notations and Terminology

Strong Convexity

• 凸函数 $f$ 满足

  $$\forall x, y \in R, \forall \lambda \in (0,1), f(\lambda x + (1-\lambda) y) \leq \lambda f(x) + (1-\lambda)f(y)$$

• 强凸函数：不等式严格不等的凸函数

  • 为保证强凸性，常添加二次项保证，如：增广拉格朗日

凸集相关标记

• $C \subseteq R^N$：非空凸集
• $x \in R^N$

• 点 $x \in R^N$ 到 $C$ 的距离为

  $$D_C(x) = \min_{y \in C} \|x-y\|_2$$

• 点 $x \in R^N$ 在 $C$ 上投影为

  $$P_Cx \in C, D_C(x) = \|x - P_Cx\|_2$$
  • $C \subseteq R^N$：闭凸集

• Indicator Function 凸集 $C$ 的示性函数为

  $$l_C(x) = \left \{ \begin{array} 0 & if x \in C \\ +\infty & if x \notin C \end{array} \right.$$

齐次函数

齐次函数：有倍数性质的函数，若变量乘以系数 $\alpha$，则新函数为原函数乘上 $\alpha^k$ 倍

$$f(\alpha x) = \alpha^k f(x)$$

• $\alpha \neq 0 \in F, x \in X$
• $f: X \rightarrow W$：域 $F$ 内两个向量空间之间的 $k$ 次齐次函数

• 线性函数 $f: X \rightarrow W$ 是一次齐次函数
• 多线性函数 $f: x_1 x_2 \cdots * x_n \rightarrow W$ 是 $n$ 次齐次函数

基本定理

• 欧拉定理：函数 $f: R^n \rightarrow R$ 可导、$k$ 次齐次函数，则有 $x \nabla f(x) = kf(x)$

次梯度

• 次梯度：实变量凸函数 $f$ 在点 $x_0$ 的次梯度 $c$ 满足

  $$\forall x, f(x) - f(x_0) \geq c(x - x_0)$$

• 可证明凸函数 $f$ 在 $x_0$ 处所有次梯度的集合 $\partial f(x)$ 是非空凸紧集

  • $\partial f(x) = [a, b]$，其中$a, b$为单侧极限

    $$\begin{align*} a & = lim_{x \rightarrow x_0^{-}} \frac {f(x) - f_0(x)} {x - x_0} \\ b & = lim_{x \rightarrow x_0^{+}} \frac {f(x) - f_0(x)} {x - x_0} \end{align*}$$

• 凸函数均指下凸函数，梯度不减

次梯度性质

运算性质

• 数乘性质

  $$\partial(\alpha f)(x) = \alpha \partial f(x), \alpha > 0$$

• 加法性质

  $$\begin{align*} f &= f_1 + f_2 + \cdots + f_m, \\ \partial f &= \partial f_1 + \cdots + \partial f_m \end{align*}$$

• 仿射性质：$f$为凸函数

  $$\begin{align*} h(x) &= f(Ax + b) \\ \partial h(x) &= A^T \partial f(Ax + b) \end{align*}$$

最优化性质

• 凸函数 $f$ 在点 $x_0$ 可导，当且仅当次梯度仅包含一个点，即该点导数

• 点 $x_0$ 是凸函数 $f$ 最小值，当且仅当次微分中包含 0 （此性质为“可导函数极小点导数为 0 ”推广）

• 负次梯度方向不一定是下降方向

次梯度求解

• 逐点（分段）极值的函数求次梯度
• 求出该点相应极值函数
• 求出对应梯度即为次梯度

Pointwise Maximum

逐点最大函数：目标函数为

$$\begin{align*} f(x) & = max \{f_1(x), f_2(x), \cdots, f_m(x)\} \\ I(x) & = \{i | f_i(x) = f(x)\} \end{align*}$$

• $I(x)$：保存 $x$ 处取值最大的函数下标

• 弱结果：$I(x)$ 中随机抽取，以 $f_i(x)$ 在该处梯度作为次梯度

• 强结果

  $$\partial f(x) = conv \cup_{i \in I(x)} \partial f_i(x)$$
  • 先求支撑平面，再求所有支撑平面的凸包
  • 可导情况实际上是不可导的特殊情况

分段函数

• 折点处

  $$\partial f(x) = conv\{a_i, a_{i+1}\} = [a_i, a_{i+1}]$$

• 非折点处

  $$\partial f(x) = {a_i}$$

$L_1$范数

PointWise Supremum

逐点上确界：目标函数为

$$\begin{align*} f(x) &= \sup_{\alpha \in A} f_{\alpha}(x) \\ I(x) &= \{\alpha \in A | f_{\alpha}(x) = f(x)\} \end{align*}$$

• 弱结果：可行梯度为

  $$\partial (\max_{\alpha} f_{\alpha}(x)) \in partial f(x)$$

• 强结果

  $$\partial f(x) = conv \cup_{\alpha \in I(x)} \partial f_{alpha}(x) \subseteq \partial f(x)$$

最大特征值

$$\begin{align*} f(x) & = \lambda_{max}(A(x)) = \sup_{\|y\|_2 = 1} \\ A(x) & = A_0 + x_1 A_1 + \cdots + x_n A_n \end{align*}$$

• $A_n$：对称矩阵

• 对确定 $\hat {x}$，$A(x)$ 最大特征值 $\lambda_{max}$、对应特征向量 $y$，则该点此梯度为

  $$(y^T A_0 y, \cdots, y^T A_n y)$$

Pointwise Inferior

逐点下确界：目标函数为

$$f(x) = \inf_y h(x, y)$$

• $h$：凸函数

• 弱结果：给定$x = \hat x$，可行次梯度为

  $$(\partial h(x, \hat y)|_{x=\hat x}, 0) \in \partial f(x)$$

复合函数

$$f(x) = h(f_1(x), \cdots, f_n(x))$$

• $h$：凸、不降函数
• $f_i$：凸函数

• 弱结果：给定$x = \hat x$，可行次梯度为

  $$g = z_1 g_1 + \cdots + z_k g_k \in \partial f(\hat x)$$

  • $z \in \partial h(f_1(\hat x), \cdots, f_k(\hat x))$
  • $g_i \in \partial f_i(\hat x)$

  • 证明

    $$\begin{align*} f(x) & \geq h(f_1(\hat x) + g_1^T(x - \hat x), \cdots, f_k(\hat x) + g_k^T(x - \hat x) \\ & \geq h(f_1(\hat x), \cdots, f_k(\hat x)) + z^T(g_1^T(x - \hat x), \cdots, g_k^T(x - \hat x)) \\ & = f(\hat x) + g^T(x - \hat x) \end{align*}$$

次梯度法

$$\begin{align*} x^{(k+1)} & = x^{(k)} + \alpha_k g^{(k)} \\ f_{best}^{(k+1)} & = min{f_{best}^{(k)}, f(x^{(k+1)})} \end{align*}$$

• $g^{(k)}$：函数$f$在$x^{(k)}$处次梯度

• 求解凸函数最优化的问题的一种迭代方法

• 相较于较内点法、牛顿法慢

  • 应用范围更广泛：能够用于不可微目标函数，目标函数可微时，无约束问题次梯度与梯度下降法有同样搜索方向
  • 空间复杂度更小
  • 可以和分解技术结合，得到简单分配算法
  • 通常不会产生稀疏解

步长选择

• 次梯度法选取步长方法很多，以下为保证收敛步长规则

• 恒定步长：$\alpha_k = \alpha$
• 恒定间隔：$\alpha_k = \gamma / |g^{(k)}|_2$
• 步长平方可加、步长不可加：$\sum{k=1}^{\infty} \alpha_k^2 < \infty, \sum{k=1}^{\infty} \alpha_k = \infty$
• 步长不可加、但递减：$lim_{k \rightarrow \infty} \alpha_k = 0$
• 间隔不可加、但递减：$lim_{k \rightarrow \gamma_k} \gamma_k = 0$

Langrangian Duality

拉格朗日对偶

• 考虑优化问题：找到$f(x)$满足约束的最好下界

  $$z^{*} = \min_{x} f(x) \\ \begin{align*} s.t. \quad & g_i(x) \leq 0, i=1,2,\cdots,m \\ & x \in X \end{align*}$$

• 考虑方程组

  $$\left \{ \begin{array}{l} f(x) < v \\ g_i(x) \leq 0, i=1,2,\cdots,m \end{array} \right.$$

  • 方程组无解：$v$是优化问题的一个下界

  • 方程组有解：则可以推出

    $$\forall \lambda \geq 0, \exists x, f(x) + \sum_{i=1}^m \lambda_ig_i(x) < v$$

    • 显然，取$g_1 + g_2 = 0, g_1(x) > 0$是反例，不能 推出原方程有解

  • 由以上方程组有解逆否命题：方程组无解充分条件如下

    $$\exists \lambda \geq 0, \min_{x} f(x) + \sum _{i=1}^m \lambda_ig_i(x) \geq v$$

• 由此方法推出的最好下界，即拉格朗日对偶问题

  $$v^{*} = \max_{\lambda \geq 0} \min_{x} f(x) + \sum_{i=1}^m \lambda_ig_i(x)$$

说明

• 拉格朗日对偶对实数域上的优化问题都存在，对目标函数、 约束函数都没有要求

• 强对偶定理：$v^{} = z^{}$，需要$f,g$满足特定条件才成立

  • 线性规划
  • 半正定规划
  • 凸优化

  • 即需要给约束条件加以限制，使得 $$\forall \lambda \geq 0, \exists x, f(x) + \sum_{i=1}^m \lambda_ig_i(x) < v$$ 是上述方程组有解的冲要条件

• 弱对偶定理：$v^{} \leq z^{}$，永远成立（以上即可证）

  • 通过弱对偶定理，可以得到原问题的一个下界
  • 对求解原问题有帮助，比如：分支界限法中快速求下界

• 对偶问题相关算法往往原问题算法在实际应用中往往更加有效

  • dual-simplex
  • primal-dual interior point method
  • augmented Lagrangian Method

原始问题

约束最优化问题

$$\begin{array}{l} \min_{x \in R^n} & f(x) \\ s.t. & c_i(x) \leq 0, i = 1,2,\cdots,k \\ & h_j(x) = 0, j = 1,2,\cdots,l \end{array}$$

Generalized Lagrange Function

• 引入Generalized Lagrange Function

  $$L(x, \alpha, \beta) = f(x) + \sum_{i=1}^k \alpha_i c_i(x) + \sum_{j=1}^l \beta_j h_j(x)$$

  • $x=(x_1, x_2, \cdots, x_n) \in R^n$
  • $\alpha_i \geq 0, \beta_j$：拉格朗日乘子

• 考虑关于x的函数

  $$\theta_P(x) = \max_{\alpha, \beta: \alpha_i \geq 0} L(x, \alpha, \beta)$$

  • $P$：primal，原始问题

  • 若x满足原始问题的两组约束条件，则$\theta_P(x)=f(x)$

  • 若x违反等式约束j，取$\beta_j \rightarrow \infty$， 则有$\theta_P(x) \rightarrow \infty$

  • 若x违反不等式约束i，取$\alpha_i \rightarrow \infty$ ，则有$\theta_P(x) \rightarrow \infty$

  则有

  $$\theta_P(x) = \left \{ \begin{array}{l} f(x), & x 满足原始问题约束条件 \\ +\infty, & 其他 \end{array} \right.$$

• 则极小化问题，称为广义拉格朗日函数的极小极大问题

  $$\min_x \theta_P(x) = \max_{\alpha, \beta: \alpha_i \geq 0} L(x, \alpha, \beta)$$

  与原始最优化问题等价，两问题最优值相同，记为

  $$p^{*} = \min_x \theta_P(x)$$

对偶问题

• 定义

  $$\theta_D (\alpha, \beta) = \min_x L(x, \alpha, \beta)$$

• 再考虑极大化$\theta_D(\alpha, \beta)$，得到广义拉格朗日 函数的极大极小问题，即

  $$\max_{\alpha, \beta: \alpha \geq 0} \theta_D(\alpha, \beta) = \max_{\alpha, \beta: \alpha \geq 0} \min_x L(x, \alpha, \beta)$$

  表示为约束最优化问题如下

  $$\begin{align*} \max_{\alpha, \beta} & \theta_D(\alpha, \beta) = \max_{\alpha, \beta} \min_x L(x, \alpha, \beta) \\ s.t. & \alpha_i \geq 0, i=1,2,\cdots,k \end{align*}$$

  称为原始问题的对偶问题，其最优值定义记为

  $$d^{*} = \max_{\alpha, \beta: \alpha \geq 0} \theta_D(\alpha, \beta)$$

原始、对偶问题关系

定理1

• 若原始问题、对偶问题都有最优值，则 $$d^{*} = \max_{\alpha, \beta: \alpha \geq 0} \min_x L(x, \alpha, \beta) \leq \min_x \max_{\alpha, \beta: \alpha \geq 0} L(x, \alpha, \beta) = p^{*}$$

• $\forall x, \alpha, \beta$有

  $$\theta_D(\alpha, \beta) = \min_x L(x, \alpha, \beta) \leq L(x, \alpha, \beta) \leq \max_{\alpha, \beta: \alpha \geq 0} = \theta_P(x)$$

  即

  $$\theta_D(\alpha, \beta) \leq \theta_P(x)$$

• 而原始、对偶问题均有最优值，所以得证

• 设$x^{}$、$\alpha^{}, \beta^{}$分别是原始问题、对偶 问题的可行解，且$d^{} = p^{*}$，则其分别是原始问题、 对偶问题的最优解

思想：最速下降&牛顿

对目标函数$f(x)$在$x^{(1)}$进行展开

$$f(x) = f(x^{(1)}) + \nabla f(x^{(1)})(x - x^{(1)})+ \frac 1 2 \nabla^2 f(x^{(1)})(x - x^{(1)})^2 + o((x - x^{(1)})^2)$$

• 最速下降法：只保留一阶项，即使用线性函数近似原目标函数
• Newton法：保留一阶、二阶项，即使用二次函数近似

• 利用近似函数求解元素问题极小值

  • 最速下降法：线性函数无极值，需要确定步长、迭代
  • Newton法：二次函数有极值，直接求导算出极值、迭代

• 最速下降法

  • 只考虑一阶导：甚至说根本没有考虑拟合原目标函数

• Newton法

  • 考虑二阶导：每步迭代还考虑了二阶导，即当前更新完毕 后，下一步能够更好的更新（二阶导的意义）
  • 甚至从后面部分可以看出，Newton法甚至考虑是全局特征， 不只是局部性质（前提目标函数性质足够好）
  • 二次函数拟合更接近函数极值处的特征

最速下降算法

思想

• 设$x=x(t)$为最优点$x$从初始点、沿负梯度方向经过的曲线， 则有

  $$\left \{ \begin{array}{l} & \frac {dx(t)} {dt} = -\nabla f(x(t)) \\ & x(t_1) = x^{(1)} \end{array} \right.$$

  • $t_1, x^{(1)}$：初始时刻、初始位置

• 可以证明，$x(t)$解存在，且$t \rightarrow \infty$时，有 $x(t) \rightarrow x^{ * }$，即得到无约束问题最优解

• 但微分方程组求解可能很麻烦，可能根本无法求解

  • 考虑将以上曲线离散化，每次前进到“不应该”前进为止
  • 然后更换方向，逐步迭代得到最优解

算法

• 搜索方向最速下降方向：负梯度方向
• 终止准则：$\nabla f(x^{(k)})=0$

1. 取初始点$x^{(1)}$，置k=1

2. 若$\nabla f(x^{(k)})=0$，则停止计算，得到最优解， 否则置

   $$d^{(k)} = -\nabla f(x^{(k)})$$

   以负梯度作为前进方向

3. 一维搜索，求解一维问题

   $$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$$

   得$\alpha_k$前进步长，置

   $$x^{(k+1)} = x^{(k)} + \alpha_k d^{(k)}$$

4. 置k=k+1，转2

• 最速下降算法不具有二次终止性

叠加惯性

模拟物体运动时惯性：指数平滑更新步长

Momentum

冲量方法：在原始更新步上叠加上次更新步，类似指数平滑

$$v^{(t)} = \gamma v^{(t-1)} + (1 - \gamma) \eta \bigtriangledown_\theta L(\theta^{(t-1)}) \\ \theta^{(t)} = \theta^{(t-1)} - v^{(t)}$$

• $v^{(t)}$：第$t$步时第k个参数更新步
• $L(\theta)$：往往是batch损失函数

• 更新参数时，一定程度保持上次更新方向
• 可以在一定程度上保持稳定性，学习速度更快
• 能够越过部分局部最优解

Nesterov Momentum

NGA：在使用冲量修正最终方向基础上，使用冲量对当前 参数位置进行修正，即使用“未来”位置计算梯度

• 先使用冲量更新一步
• 再在更新后位置计算新梯度进行第二步更新

$$v^{(t)} = \gamma v^{(t-1)} + \eta \bigtriangledown_\theta L(\theta^{(t-1)} - \gamma v^{(t-1)}) \\ \theta^{(t)} = \theta^{(t-1)} - v^{(t)}$$

动态学习率

• 学习率太小收敛速率缓慢、过大则会造成较大波动
• 在训练过程中动态调整学习率大小较好

• 模拟退火思想：达到一定迭代次数、损失函数小于阈值时，减小 学习速率

Vanilla Gradient Descent

每次迭代减小学习率$\eta$

$$\eta^{(t)} = \frac \eta {\sqrt {t+1}} \\ \theta^{(t)} = \theta^{(t-1)} - \eta^{(t)} \bigtriangledown_\theta L(\theta^{(t-1)})$$

• 学习率逐渐减小，避免学习后期参数在最优解附近反复震荡

Adagrad

adaptive gradient：训练中不同参数学习率随着迭代次数、 梯度动态变化，使得参数收敛更加平稳

$$v^{(t)}_k = \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ \theta^{(t)}_k = \theta^{(t-1)}_k - \frac \eta {\sqrt {\sum_{i=0}^{t-1} (v^{(i)}_k)^2 + \epsilon}} v^{(t)}_k$$

• $\epsilon$：fuss factor，避免分母为0
• $\theta^{(t)}_k$：第t轮迭代完成后待估参数第k个分量 （之前未涉及参数间不同，统一为向量）

• 特点

  • 较大梯度参数真正学习率会被拉小；较小梯度真正学习率 参数被拉小幅度较小
  • 可以和异步更新参数结合使用，给不常更新参数更大学习率

• 缺点

  • 在训练后期，分母中梯度平方累加很大，学习步长趋于0， 收敛速度慢（可能触发阈值，提前结束训练）

RMSprop

root mean square prop：指数平滑更新学习率分母

$$v^{(t)}_k = \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ \theta^{(t)}_k = \theta^{(t-1)}_k - \frac \eta {\sqrt { \gamma \sum_{i=1}^{t-1}(v^{(i)}_k)^2 + (1 - \gamma)((v^{(t)})^2 + \epsilon} } v^{(t)}$$

• 赋予当前梯度更大权重，减小学习率分母，避免学习速率下降 太快

Adam

adptive moment estimation：指数平滑更新步、学习率分母

$$\begin{align*} v^{(t)}_k & = \gamma_1 v^{(t-1)}_k + (1 - \gamma_1) \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ s^{(t)}_k & = \gamma_2 s^{(t-1)}_k + (1 - \gamma_2) \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \hat{v^{(t)}_k} & = \frac {v^{(t)}_k} {1 - \gamma_1^t} \\ \hat{s^{(t)}_k} & = \frac {s^{(t)}_k} {1 - \gamma_2^t} \\ \theta^{(t)}_k & = \theta^{(t-1)}_k - \frac \eta {\sqrt{\hat{s^{(t)}_k} + \epsilon}} \hat{v^{(t)}_k} \end{align*}$$

• $\gamma_1$：通常为0.9
• $\gamma_2$：通常为0.99
• $\hat{v^{(t)}_k} = \frac {v^{(t)}_k} {1 - \gamma_1^t}$ ：权值修正，使得过去个时间步，小批量随机梯度权值之和为1

• 利用梯度的一阶矩$v^{(t)}$、二阶矩$s^{(t)}$动态调整每个 参数学习率

• 类似于mommentum、RMSprop结合

• 经过偏执矫正后，每次迭代学习率都有确定范围，参数比较平稳

Adadelta

指数平滑更新学习率（分子）、学习率分母

$$\begin{align*} s^{(t)}_k & = \gamma_1 s^{(t-1)}_k + (1 - \gamma_1) \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \hat{v^{(t)}_k} & = \sqrt {\frac {\Delta \theta^{(t-1)}_k + \epsilon} {s^{(t)}_k + \epsilon}} \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \Delta \theta^{(t)}_k & = \gamma_1 \Delta \theta^{(t-1)}_k + (1 - \gamma_1) \hat{v^{(t)}_k}^2 \\ \theta^{(t)}_k & = \theta^{(t)}_k - \hat{v^{(t)}_k} \end{align*}$$

• $s, \Delta \theta$共用超参$\gamma_1$

• 在RMSprop基础上，使用$\sqrt {\Delta \theta}$作为学习率
• $\hat v$：中超参$\gamma_1$在分子、分母“抵消”，模型对 超参不敏感

样本量

Singular Loss/Stocastic Gradient Descent

SGD：用模型在某个样本点上的损失极小化目标函数、计算梯度、 更新参数

• 单点损失度量模型“一次”预测的好坏

  • 代表模型在单点上的优劣，无法代表模型在总体上性质
  • 具有很强随机性

• 单点损失不常用，SGD范围也不局限于单点损失

• 损失函数具体参见ml_xxxxx

全局估计

全局损失：用模型在全体样本点上损失极小化目标函数、计算梯度、 更新参数

$$\theta^{(t)} = \theta^{(t-1)} - \eta \bigtriangledown_\theta L_{total}(\theta_{(t-1)})$$

• $\theta^{(t)}$：第t步迭代完成后待估参数
• $\eta$：学习率
• $L{total}(\theta) = \sum{i=1}^N L(\theta, x_i, y_i)$： 训练样本整体损失
• $N$：训练样本数量

• 若损失函数有解析解、样本量不大，可一步更新（计算） 完成（传统参数估计场合）

  • 矩估计
  • 最小二乘估计
  • 极大似然估计

• 否则需要迭代更新参数

  • 样本量较大场合
  • 并行计算

Mini-Batch Loss

mini-batch loss：用模型在某个batch上的损失极小化目标函数、 计算梯度、更新参数

$$\theta^{(t)} = \theta^{(t-1)} - \eta \bigtriangledown_\theta L_{batch}(\theta^{(t-1)})$$

• $L{batch}(\theta)=\sum{i \in B} L(\theta, x_i, y_i)$： 当前batch整体损失
• $B$：当前更新步中，样本组成的集合batch

• batch-loss是模型在batch上的特征，对整体的代表性取决于 batch大小

  • batch越大对整体代表性越好，越稳定；越小对整体代表 越差、不稳定、波动较大、难收敛
  • batch大小为1时，就是SGD
  • batch大小为整个训练集时，就是经验（结构）风险

• batch-loss是学习算法中最常用的loss，SGD优化常指此

  • 实际中往往是使用batch-loss替代整体损失，表示经验风险 极小化
  • batch-loss同样可以带正则化项，表示结构风险极小化
  • 损失极值：SVM（几何间隔最小）

优点

• 适合样本量较大、无法使用样本整体估计使用
• 一定程度能避免局部最优（随机batch可能越过局部极值）
• 开始阶段收敛速度快

缺点

• 限于每次只使用单batch中样本更新参数，batch-size较小时， 结果可能不稳定，往往很难得到最优解

• 无法保证良好的收敛性，学习率小收敛速度慢，学习率过大 则损失函数可能在极小点反复震荡

• 对所有参数更新应用相同学习率，没有对低频特征有优化 （更的学习率）

• 依然容易陷入局部最优点

Newton法

思想

• 若$x^{ * }$是无约束问题局部解，则有

  $$\nabla f(x^{ * }) = 0$$

  可求解此问题，得到无约束问题最优解

• 原始问题是非线性，考虑求解其线性逼近，在初始点$x^{(1)}$ 处泰勒展开

  $$\nabla f(x) \approx \nabla f(x^{(1)}) + \nabla^2 f(x^{(1)})(x - x^{(1)})$$

  解得

  $$x^{(2)} = x^{(1)} - (\nabla^2 f(x^{(1)}))^{-1} \nabla f(x^{(1)})$$

  作为$x^{ * }$的第二次近似

• 不断迭代，得到如下序列

  $$x^{(k+1)} = x^{(k)} + d^{(k)}$$

  • $d^{(k)}$：Newton方向，即以下方程解 $$\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$$

算法

• 初始点 $x^{(1)}$、精度要求 $\epsilon$，置 $k=1$

• 考虑 $|\nabla f(x^{(k)})| \leq \epsilon$

  • 若满足，则停止计算，得到最优解 $x^{(k)}$

  • 否则求解如下方程，得到 $d^{(k)}$

    $$\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$$

• 如下设置，并转2

  $$x^{(k+1)} = x^{(k)} + d^{(k)}, k = k+1$$

特点

• 优点

  • 产生点列 ${x^{k}}$ 若收敛，则具有二阶收敛速率
  • 具有二次终止性，事实上对正定二次函数，一步即可收敛

• 缺点

  • 可能会在某步迭代时目标函数值上升
  • 当初始点 $x^{(1)}$ 距离最优解 $x^{ * }$ 时，产生的点列 可能不收敛，或者收敛到鞍点
  • 需要计算 Hesse 矩阵
    • 计算量大
    • Hesse 矩阵可能不可逆，算法终止
    • Hesse 矩阵不正定，Newton 方向可能不是下降方向

阻尼/修正 Newton 法

• 克服 Newton 法目标函数值上升的缺点
• 一定程度上克服点列可能不收敛缺点

算法

• 初始点 $x^{(1)}$、精度要求 $\epsilon$，置 $k=1$

• 考虑 $|\nabla f(x^{(k)})| \leq \epsilon$

  • 若满足，停止计算，得到最优解 $x^{(k)}$
  • 否则求解如下方程得到 $d^{(k)}$ $$\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$$

• 一维搜索，求解一维问题

  $$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$$

  得到 $\alpha_k$，如下设置并转2

  $$x^{(k+1)} = x^{(k)} + \alpha_k d^{(k)}, k = k+1$$

其他改进

• Newton 法、修正 Newton 法的改进方向
  • 结合最速下降方向修正迭代方向
  • Hesse 矩阵不正定情形下的替代

结合最速下降方向

• 将 Newton 方向和最速下降方向结合

• 设 $\theta_k$ 是 $$ 之间夹角，显然希望 $\theta < \frac \pi 2$

• 则置限制条件 $\eta$，取迭代方向

  $$d^{(k)} = \left \{ \begin{array}{l} d^{(k)}, & cos\theta_k \geq \eta \\ -\nabla f(x^{(k)}), & 其他 \end{array} \right.$$

Negative Curvature

• 当 Hesse 矩阵非正定时，选择负曲率下降方向 $d^{(k)}$（一定存在）

• Hesse 矩阵非正定时，一定存在负特征值、相应特征向量 $u$

  • 取负曲率下降方向作为迭代方向

    $$d^{(k)} = -sign(u^T \nabla f(x^{(k)})) u$$

  • $x^{(k)}$ 处负曲率方向 $d^{(k)}$ 满足

    $${d^{(k)}}^T \nabla^2 f(x^{(k)}) d^{(k)} < 0$$

修正 Hesse 矩阵

• 取迭代方向 $d^{(k)}$ 为以下方程的解

  $$(\nabla^2 f(x^{(k)}) + v_k I) d = -\nabla f(x^{k})$$

• $v_k$：大于 $\nabla^2 f(x^{(k)})$ 最大负特征值绝对值