Gradient Descent Method
思想:最速下降&牛顿
对目标函数$f(x)$在$x^{(1)}$进行展开
- 最速下降法:只保留一阶项,即使用线性函数近似原目标函数
- Newton法:保留一阶、二阶项,即使用二次函数近似
利用近似函数求解元素问题极小值
- 最速下降法:线性函数无极值,需要确定步长、迭代
- Newton法:二次函数有极值,直接求导算出极值、迭代
最速下降法
- 只考虑一阶导:甚至说根本没有考虑拟合原目标函数
Newton法
- 考虑二阶导:每步迭代还考虑了二阶导,即当前更新完毕 后,下一步能够更好的更新(二阶导的意义)
- 甚至从后面部分可以看出,Newton法甚至考虑是全局特征, 不只是局部性质(前提目标函数性质足够好)
- 二次函数拟合更接近函数极值处的特征
最速下降算法
思想
设$x=x(t)$为最优点$x$从初始点、沿负梯度方向经过的曲线, 则有
- $t_1, x^{(1)}$:初始时刻、初始位置
可以证明,$x(t)$解存在,且$t \rightarrow \infty$时,有 $x(t) \rightarrow x^{ * }$,即得到无约束问题最优解
但微分方程组求解可能很麻烦,可能根本无法求解
- 考虑将以上曲线离散化,每次前进到“不应该”前进为止
- 然后更换方向,逐步迭代得到最优解
算法
- 搜索方向最速下降方向:负梯度方向
- 终止准则:$\nabla f(x^{(k)})=0$
取初始点$x^{(1)}$,置k=1
若$\nabla f(x^{(k)})=0$,则停止计算,得到最优解, 否则置
以负梯度作为前进方向
一维搜索,求解一维问题
得$\alpha_k$前进步长,置
置k=k+1,转2
- 最速下降算法不具有二次终止性
叠加惯性
模拟物体运动时惯性:指数平滑更新步长
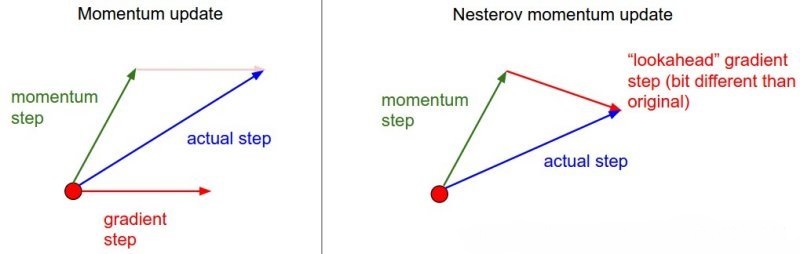
Momentum
冲量方法:在原始更新步上叠加上次更新步,类似指数平滑
- $v^{(t)}$:第$t$步时第k个参数更新步
- $L(\theta)$:往往是batch损失函数
- 更新参数时,一定程度保持上次更新方向
- 可以在一定程度上保持稳定性,学习速度更快
- 能够越过部分局部最优解
Nesterov Momentum
NGA:在使用冲量修正最终方向基础上,使用冲量对当前 参数位置进行修正,即使用“未来”位置计算梯度
- 先使用冲量更新一步
- 再在更新后位置计算新梯度进行第二步更新
动态学习率
- 学习率太小收敛速率缓慢、过大则会造成较大波动
- 在训练过程中动态调整学习率大小较好
- 模拟退火思想:达到一定迭代次数、损失函数小于阈值时,减小 学习速率
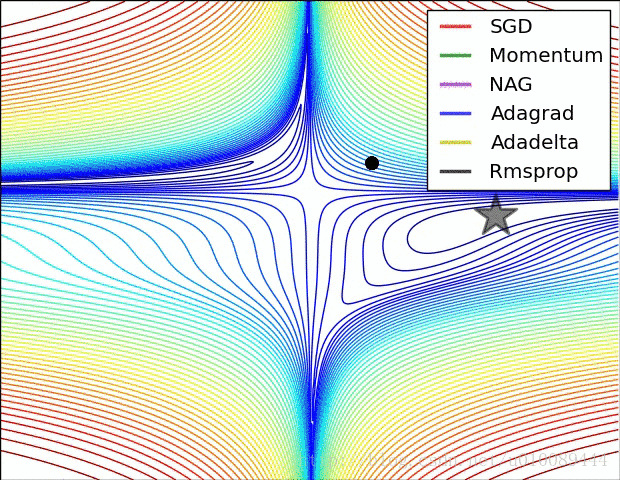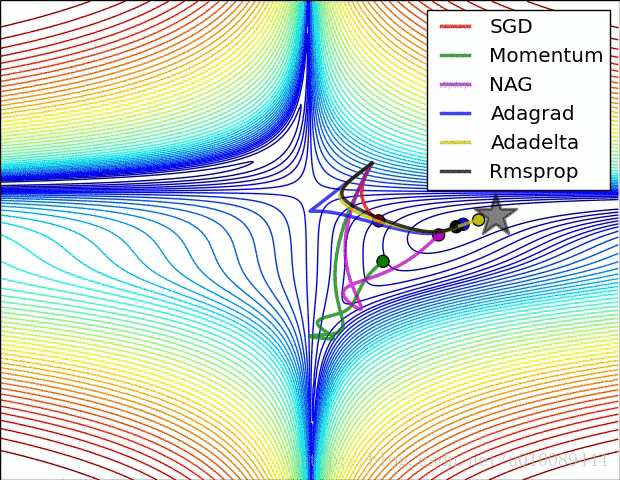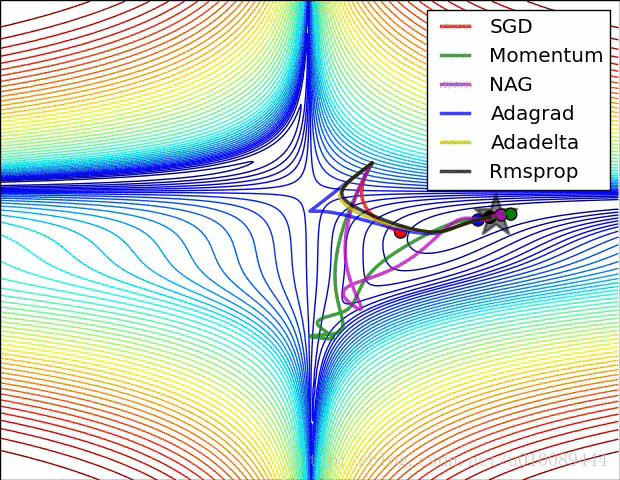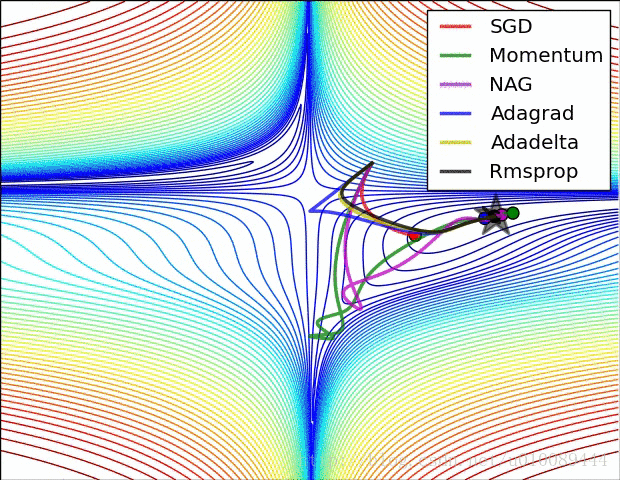
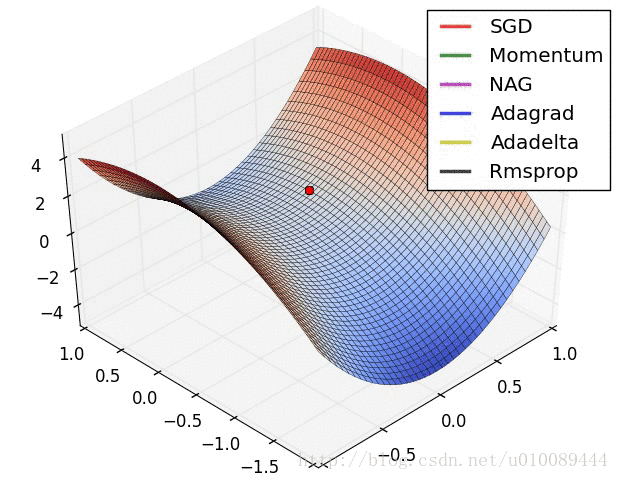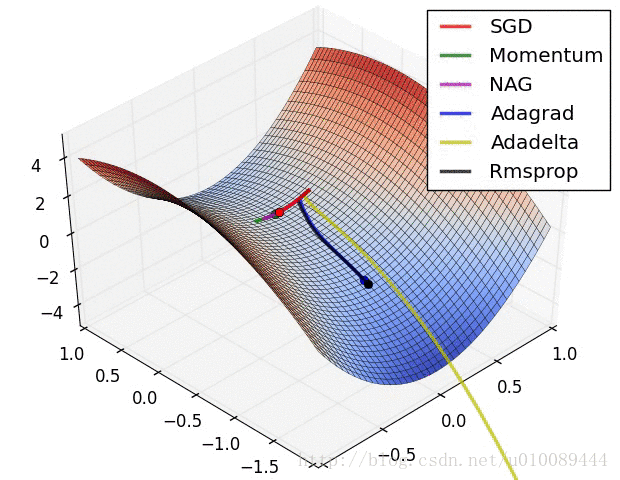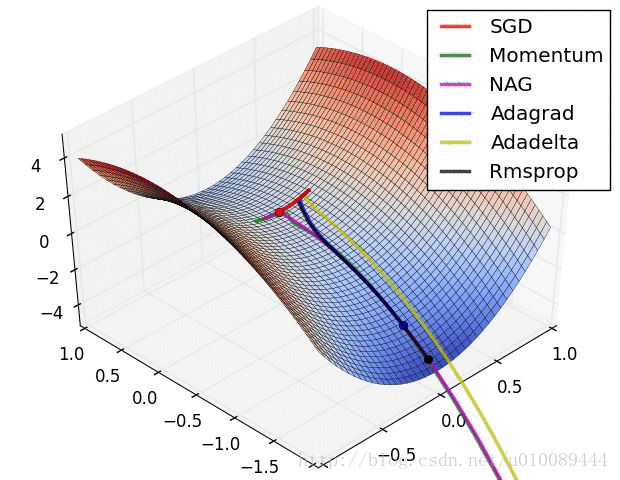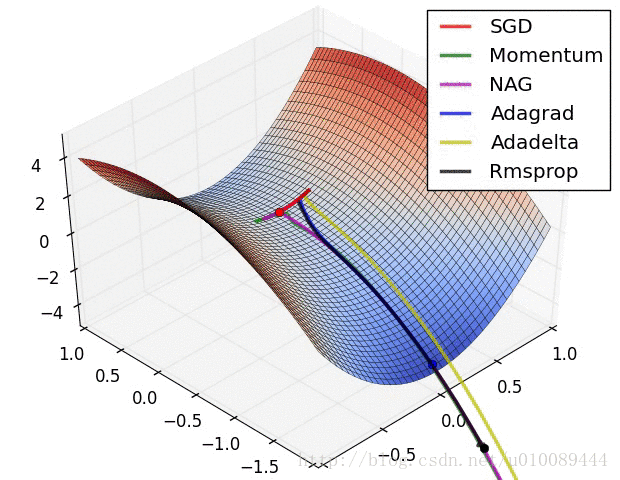
Vanilla Gradient Descent
每次迭代减小学习率$\eta$
- 学习率逐渐减小,避免学习后期参数在最优解附近反复震荡
Adagrad
adaptive gradient:训练中不同参数学习率随着迭代次数、 梯度动态变化,使得参数收敛更加平稳
- $\epsilon$:fuss factor,避免分母为0
- $\theta^{(t)}_k$:第t轮迭代完成后待估参数第k个分量 (之前未涉及参数间不同,统一为向量)
特点
- 较大梯度参数真正学习率会被拉小;较小梯度真正学习率 参数被拉小幅度较小
- 可以和异步更新参数结合使用,给不常更新参数更大学习率
缺点
- 在训练后期,分母中梯度平方累加很大,学习步长趋于0, 收敛速度慢(可能触发阈值,提前结束训练)
RMSprop
root mean square prop:指数平滑更新学习率分母
- 赋予当前梯度更大权重,减小学习率分母,避免学习速率下降 太快
Adam
adptive moment estimation:指数平滑更新步、学习率分母
- $\gamma_1$:通常为0.9
- $\gamma_2$:通常为0.99
- $\hat{v^{(t)}_k} = \frac {v^{(t)}_k} {1 - \gamma_1^t}$ :权值修正,使得过去个时间步,小批量随机梯度权值之和为1
利用梯度的一阶矩$v^{(t)}$、二阶矩$s^{(t)}$动态调整每个 参数学习率
类似于mommentum、RMSprop结合
经过偏执矫正后,每次迭代学习率都有确定范围,参数比较平稳
Adadelta
指数平滑更新学习率(分子)、学习率分母
- $s, \Delta \theta$共用超参$\gamma_1$
- 在RMSprop基础上,使用$\sqrt {\Delta \theta}$作为学习率
- $\hat v$:中超参$\gamma_1$在分子、分母“抵消”,模型对 超参不敏感
样本量
Singular Loss/Stocastic Gradient Descent
SGD:用模型在某个样本点上的损失极小化目标函数、计算梯度、 更新参数
单点损失度量模型“一次”预测的好坏
- 代表模型在单点上的优劣,无法代表模型在总体上性质
- 具有很强随机性
单点损失不常用,SGD范围也不局限于单点损失
- 损失函数具体参见ml_xxxxx
全局估计
全局损失:用模型在全体样本点上损失极小化目标函数、计算梯度、 更新参数
- $\theta^{(t)}$:第t步迭代完成后待估参数
- $\eta$:学习率
- $L{total}(\theta) = \sum{i=1}^N L(\theta, x_i, y_i)$: 训练样本整体损失
- $N$:训练样本数量
若损失函数有解析解、样本量不大,可一步更新(计算) 完成(传统参数估计场合)
- 矩估计
- 最小二乘估计
- 极大似然估计
否则需要迭代更新参数
- 样本量较大场合
- 并行计算
Mini-Batch Loss
mini-batch loss:用模型在某个batch上的损失极小化目标函数、 计算梯度、更新参数
- $L{batch}(\theta)=\sum{i \in B} L(\theta, x_i, y_i)$: 当前batch整体损失
- $B$:当前更新步中,样本组成的集合batch
batch-loss是模型在batch上的特征,对整体的代表性取决于 batch大小
- batch越大对整体代表性越好,越稳定;越小对整体代表 越差、不稳定、波动较大、难收敛
- batch大小为1时,就是SGD
- batch大小为整个训练集时,就是经验(结构)风险
batch-loss是学习算法中最常用的loss,SGD优化常指此
- 实际中往往是使用batch-loss替代整体损失,表示经验风险 极小化
- batch-loss同样可以带正则化项,表示结构风险极小化
- 损失极值:SVM(几何间隔最小)
优点
- 适合样本量较大、无法使用样本整体估计使用
- 一定程度能避免局部最优(随机batch可能越过局部极值)
- 开始阶段收敛速度快
缺点
限于每次只使用单batch中样本更新参数,batch-size较小时, 结果可能不稳定,往往很难得到最优解
无法保证良好的收敛性,学习率小收敛速度慢,学习率过大 则损失函数可能在极小点反复震荡
对所有参数更新应用相同学习率,没有对低频特征有优化 (更的学习率)
依然容易陷入局部最优点
Gradient Descent Method
https://xyy15926.github.io/Math-Analysis/Optimization/gredient_based.html

