Norm

$\mathcal{L_p}$ 范数

• $\mathcal{L_p}$ 范数

  $$\|x\|_p = (|x_1|^p + |x_2|^p + \cdots + |x_N|^p)^{1/p}$$

  • $x \in R^n$

• $\mathcal{L_p}$ Dual Norm 对偶范数

  $$\|x\|^{*} = \mathop \sup_{z}{x^Tz|\|z\| \leq 1}$$

  • $x \in R^N$
  • $|x|$：$x$的某个范数

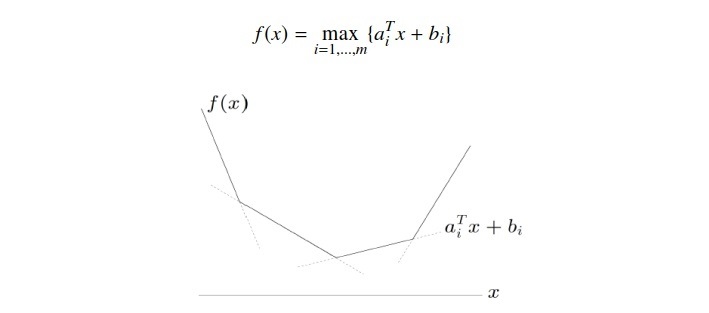
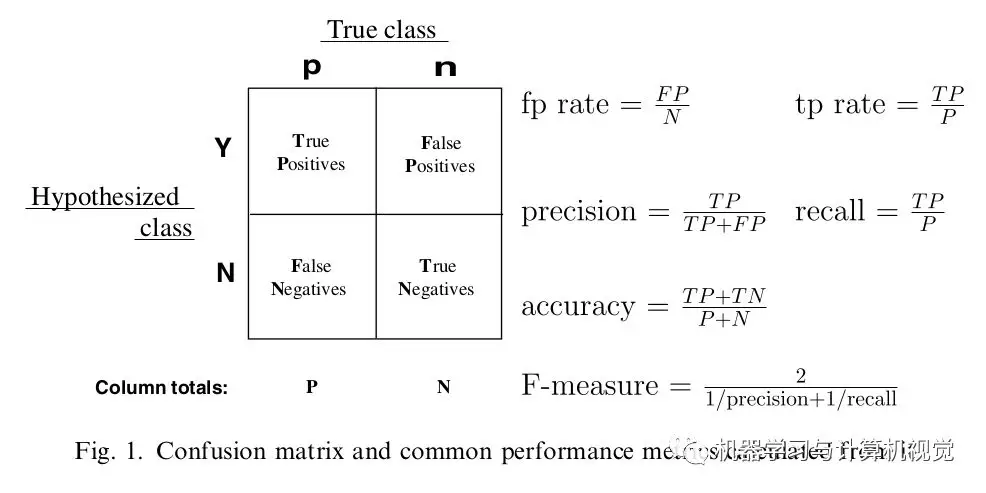
无约束局部解

$$minf(x), x \in R^n$$

• 若存在$x^{ } \in R^n, \epsilon > 0, \forall x \in R^n$ 使得$|x - x^{ }| < \epsilon$时，恒有
• $f(x) \geq f(x^{ })$：则称$x^{ }$为f(x)的 local minimum point/solution（局部极小点/局部解）
• $f(x) > f(x^{ })$：则称$x^{ }$为f(x)的 严格局部极小点/局部解

最优性条件

First-Order Necessary Condtion

• 无约束问题局部解的一阶必要条件：设f(x)有连续的一阶偏导， 弱$x^{ * }$是无约束问题的局部解，则 $$\triangledown f(x{* }) = 0$$

Second-Order Necessary Condition

• 无约束问题局部解的二阶必要条件：设f(x)有连续二阶偏导， 若$x^{ * }$是无约束问题的局部解，则

  • $$\triangledown f(x^{ * }) = 0$$
  • $$\triangledown^2 f(x^{ * })半正定$$

Second-Order Sufficient Condition

• 无约束问题局部解的二阶充分条件：设f(x)有连续二阶偏导， 若在$x^{ }$处满足以下，则x^{ }是无约束问题的 严格局部解

  • $$\triangledown f(x^{ * }) = 0$$
  • $$\triangledown^2 f(x^{ * })正定$$

下降算法

迭代算法：将当前迭代点向正确方向移动一定步长，然后 检验目标值是否满足一定要求

• 方向、步长就是不同优化算法主要关心的两个方面
• 还关心算法的rate of convergence（收敛速率）

一般下降算法框架

1. 取初始点$x^{(1)}$，置精度要求$\epsilon$，置k=1

2. 若在点$x^{(k)}$处满足某个终止准则，则停止计算，得无约束 优化问题最优解$x^{(k)}$，否则适当地选择$x^{(k)}$处 搜索方向

3. 进行适当的一维搜索，求解一维问题

   $$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$$

4. 置k=k+1，转2

要使下降算法可行，需要确定

• 某点出搜索方向
  • 负梯度方向
  • Newton方向：求方向的时候已确定步长，也可用做步长搜索
  • 拟Newton方向
• 求步长地一维搜索方式
  • 试探法
    • 0.618法
    • Fibonacci方法（分数法）
    • 二分法
  • 插值法
    • 三点二次插值法
    • 二点二次插值法
    • 两点三次插值法
  • 非精确一维搜索方法
    • Glodstein方法
    • Armijo方法
    • Wolfe-Powell方法

• 算法终止准则

  • $|\triangledown f(x^{(k)})| < \epsilon$
  • $|x^{(k+1)} - x^{(k)}| < \epsilon$
  • $|f(x^{(k+1)}) - f(x^{(k)})| < \epsilon$

  • 实际计算中最优解可能永远无法迭代达到，应该采用较弱 终止准则

算法收敛性

• 收敛：序列${x^{(k)}}$或其一个子列（仍记${x^{(k)}}$） 满足 $$\lim_{k \rightarrow \infty} x^{(k)} = x^{ * }$$

  • $x^{ * }$：无约束问题局部解

但是这样强的结果难以证明

• 往往只能证明${x^{(k)}}$的任一聚点的稳定点
• 或是更弱的 $$\lim_{k \rightarrow \infty} inf \|\triangledown f(x^{(k)}) \| = 0$$

• 局部收敛算法：只有初始点充分靠近极小点时，才能保证产生 序列收敛
• 全局收敛算法：对任意初始点，产生序列均能收敛

收敛速率

设序列${x^{(k)}}$收敛到$x^{ * }$，若以下极限存在

$$\lim _ {k \rightarrow \infty} \frac {\|x^{(k+1)} - x^{*}\|} {\|x^{(k)} - x^{*}\|} = \beta$$

• $0 < \beta < 1$：线性收敛
• $\beta = 0$：超线性收敛
• $\beta = 1$：次线性收敛（收敛速率太慢，一般不考虑）

算法的二次终止性

• 二次终止性：若某算法对任意正定二次函数，从任意初始点出发 ，都能经过有限步迭代达到其极小点，则称该算法有二次终止性

具有二次终止性的算法被认为时好算法，否则计算效果较差，原因

• 正定二次目标函数有某些好的性质，好的算法应该能在有限步内 达到其极小点

• 对于一个一般的目标函数，若其在极小点处的Hesse矩阵 $\triangledown f(x^{( * )})$，则由泰勒展开式得到

  $$\begin{align*} f(x) & = f(x^{*}) + \triangledown f(x^ {*})^T(x - x^{*}) \\ & + \frac 1 2 (x - x^{*})^T \triangledown^2 f(x^{*}) (x - x^{*}) \\ & + o(\|x - x^{*}\|^2) \end{align*}$$

  即目标函数f(x)在极小点附近与一个正定二次函数近似，所以对 正定二次函数好的算法，对一般目标函数也应该具有较好的性质

Linear Programming

数学模型

一般数学模型

线性规划问题（LP）可以抽象为一般的数学模型

$$\begin{array}{l} (\min_x, \max_x) & S=c_1 x_1 + c_2 x_2 + \cdots + c_n x_n \\ s.t. & \left \{ \begin{array} {l} a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n (\geq = \leq) b_1 \\ a_{2,1} x_1 + a_{2,2} x_2 + \cdots + a_{2,n} x_n (\geq = \leq) b_2 \\ \vdots \\ a_{m,1} x_1 + a_{m,2} x_2 + \cdots + a_{m,n} x_n (\geq = \leq) b_m \end{array} \right. \end{array}$$

• $S = c_1 x_1 + c_2 x_2 + \cdots + c_n x_n$：目标函数
• $x_1, x_2, …, x_n$：待求解变量
• $bi、c_i、a{ij}$：实常数
• $(\geq = \leq)$：在三种符号中取一种

标准形式

$$\begin{array}{l} \min_x & S=c_1 x_1 + c_2 x_2 + \cdots + c_n x_n \\ s.t. & a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n = b_1 \\ & \vdots \\ & a_{t,1} x_1 + a_{t,2} x_2 + \cdots + a_{t,n} x_n = b_t \\ & a_{t+1,1} x_1 + a_{t+1,2} x_2 + \cdots + a_{t+1, n} x_n \leq b_{t+1} \\ & \vdots \\ & a_{t+l,1} x_1 + a_{t+l,2} x_2 + \cdots + a_{t+l, n} x_n \leq b_{t+l} \\ \end{array}$$

• $\max_x$：目标函数取翻转换为$\min_x$

• $\geq$：不等式左右取反转换为$\leq$

• 线性规划一般模式都可以等价转换为标准形式

Simplex Method

单纯型法：利用线性规划极值点必然在单纯型顶点取得，不断迭代顶点求出极值

算法

• 初始化：标准化线性规划问题，建立初始表格
  • 最小化目标函数：目标函数系数取反，求极大
  • 不等式约束：加入松弛变量（代表不等式两端差值）
  • 变量非负：定义为两个非负变量之差
• 最优测试
  • 若目标行系数都为非负，得到最优解，迭代停止
  • 基变量解在右端列中，非基变量解为 0
• 确定主元列
  • 从目标行的前 $n$ 个单元格中选择一个非负单元格，确定主元列
  • 选择首个非负：解稳定，若存在最优解总是能取到
  • 选择绝对值最大：目标函数下降快，但有可能陷入死循环，无法得到最优解（不满足最优条件）

• 确定主元（分离变量）（行）

  • 对主元列所有正系数，计算右端项和其比值 $\Theta$ 比率
  • 最小 $\Theta$ 比率确定主元（行）（类似的为避免死循环，总是选择首个最小者）

• 转轴变换（建立新单纯形表）

  • 主元变 1：主元行所有变量除以主元
  • 主元列变 0：其余行减去其主元列倍主元行
  • 交换基变量：主元行变量标记为主元列对应变量

特点

• 算法时间效率
  • 极点规模随着问题规模指数增长，所以最差效率是指数级
  • 实际应用表明，对 $m$ 个约束、$n$ 个变量的问题，算法迭代次数在 $m$ 到 $3m$ 之间，每次迭代次数正比于 $nm$
• 迭代改进

Two-Phase Simplex Method

两阶段单纯形法：单纯型表中没有单元矩阵，无法方便找到基本可行解时使用

• 在给定问题的约束等式中加入人工变量，使得新问题具有明显可行解
• 利用单纯形法求解最小化新的线性规划问题

其他一些算法

• 大 M 算法
• Ellipsoid Method 椭球算法
  • 算法时间效率
    • 可以在多项式时间内对任意线性规划问题求解
    • 实际应用效果较单纯形法差，但是最差效率更好
• Karmarkar 算法
  • 内点法（迭代改进）

凸优化

$$\begin{array}{l} \min_x & f(x) \\ s.t. & g_i(x) \leq 0, i=1，2,\cdots,k \\ & h_i(x) = 0, i=1,2,\cdots,l \end{array}$$

• $f(x), g(x)$：$R^n$ 上连续可微的凸函数
• $h_i(x)$：$R^n$ 上仿射函数
• 仿射函数：满足 $f(x)=ax+b, a \in R^n, b \in R, x \in R^n$

二次规划

$$\begin{array}{l} \min_x & f(x)=\frac 1 2 x^TGx + c^Tx \\ s.t. & Ax \leq b \end{array}$$

• $G \in R^{n * n}$：$n$ 阶实对称矩阵
• $A \in R^{m n}$：$m n$ 实矩阵
• $b \in R^m$
• $c \in R^n$

• $G$ 正定

  • 此时目标函数 $f(x)$ 为凸函数
  • 凸二次规划
  • 问题有唯一全局最小值
  • 问题可可由椭球法在多项式时间内求解

• $G$ 半正定

  • 此时目标函数 $f(x)$ 为凸函数
  • 半定规划
  • 若约束条件可行域不空，且目标函数在此可行域有下界，则问题有全局最小值

• $G$非正定

  • 目标函数有多个平稳点（局部极小），NP-hard 问题

求解

• 椭球法
• 内点法
• 增广拉格朗日法
• 投影梯度法

二阶锥规划

$$\begin{array}{l} \min_x & f^Tx \\ s.t. & \|A_ix + b_i \|_2 \leq c_i^Tx + d_i, i=1,2,\cdots,m \\ & Bx=g \end{array}$$

• $f \in R^n$
• $A_i \in R^{n_i * n}$，$b_i \in R^{n_i}$，$c_i \in R^{n_i}$，$d_i \in R$
• $B \in R^{p * n}$，$g \in R^n$

• $A_i=0,i=1,\cdots,m$：退化为线性规划

• 一般的二阶规划可以转换为二阶锥规划

  $$X^TAX + qTX + C \leq 0 \Rightarrow \|A^{1/2}x + \frac 1 2 A^{-1/2}q\|^{1/2} \leq -\frac 1 4 q^TA^{-1}q - c$$

• 二阶锥规划可以使用内点法很快求解（多项式时间）

非线性最小二乘

$$\begin{align*} f(x) & = \frac 1 2 \sum_{i=1}^m r^2_i(x) \\ & = \frac 1 2 r(x) r^T(x) \end{align*}$$

• $r_i(x)$：通常为非线性函数
• $r(x) = (r_1(x), \cdots, r_n(x))^T$
• $x \in R^n, m \geq n$

• 考虑目标函数梯度、Hesse 矩阵

  $$\begin{align*} \nabla f(x) & = \sum_{i=1}^m \nabla r_i(x) r_i(x) \\ & = J(x)^T r(x) \\ \nabla^2 f(x) & = \sum_{i=1}^m \nabla r_i(x) r_i(x) + \sum_{i=1}^m r_i \nabla^2 r_i(x) \\ & = J(x)^T J(x) + \sum_{i=1}^m r_i(x) \nabla^2 r_i(x) \end{align*}$$

• $$J(x) = \begin{bmatrix} \frac {\partial r_1} {\partial x_1} & \frac {\partial r_1} {\partial x_2} & \cdots & \frac {\partial r_1} {\partial x_n} \\ \frac {\partial r_2} {\partial x_1} & \frac {\partial r_2} {\partial x_2} & \cdots & \frac {\partial r_2} {\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial r_m} {\partial x_1} & \frac {\partial r_m} {\partial x_2} & \cdots & \frac {\partial r_m} {\partial x_n} \end{bmatrix} = \begin{bmatrix} \nabla r_1(x)^T \\ \nabla r_2(x)^T \\ \vdots \\ \nabla r_m(x)^T \\ \end{bmatrix}$$ 为$r(x)$的 Jacobi 矩阵

Gauss-Newton 法

• 为简化计算，略去 Newton 法中 Hesse 矩阵中 $\sum_{i=1}^m r_i(x) \nabla^2 r_i(x)$ 项，即直接求解方程组

  $$J(x^{(k)})^T J(x^{(k)}) d = -J(x^{(k)})^T r(x^{(k)})$$

• 求解同一般 Newton 法

特点

• 实际问题中

  • 局部解 $x^{ }$ 对应的目标函数值 $f(x^{ })$ 接近 0 时，采用 Gauss-Newton 法效果较好，此时
    • $|r(x^{(k)})|$ 较小
    • 曲线$r_i(x)$接近直线
    • $\nabla^2 r_i(x) \approx 0$
  • 否则效果一般

• 矩阵 $J(x^{(k)})^T J(x^{(k)})$ 是半正定矩阵

  • 当 Jacobi 矩阵列满秩时为正定矩阵，此时虽然 $d^{(k)}$ 是下降方向，但仍需类似修正牛顿法增加一维搜索策略保证目标函数值不上升

Levenberg-Marquardt 方法

• 考虑到 $J(x^{(k)})$ 中各列线性相关、接近线性相关，求解 Newton-Gauss 方法中的方程组会出现困难，可以改为求解

  $$(J(x^{(k)})^T J(x^{(k)}) + vI) d = -J(x^{(k)})^T r(x^{(k)})$$

• $v$：迭代过程中需要调整的参数，LM 方法的关键即如何调整

定理1

• 若 $d(v)$ 是以上方程组的解，则 $|d(v)|^2$ 是 $v$ 的连续下降函数，且 $v \rightarrow +\infty, |d(v)| \rightarrow 0$

• $J(x^{(k)})^T J(x^{(k)})$ 是对称半正定矩阵，则存在正交阵

  $$(P^{(k)})^T J(x^{(k)})^T J(x^{(k)}) P^{(k)} = \Lambda^{(k)}$$

• 则可以解出 $|d(v)|^2$

• 增大 $v$ 可以限制 $|d^{(k)}|$，所以 LM 方法也被称为阻尼最小二乘法

定理2

• 若 $d(v)$ 是以上方程的解，则 $d(v)$ 是 $f(x)$ 在 $x^{(k)}$ 处的下降方向，且 $v \rightarrow + \infty$ 时，$d(v)$ 的方向与 $-J(x^{(k)})^T r(x^{(k)})$ 方向一致

• 下降方向：$\nabla f(x^{(k)}) d(v) < 0$ 即可
• 方向一致：夹角余弦

• $v$充分大时，LM 方法产生的搜索方向 $d^{(k)}$ 和负梯度方向一致

参数调整方法

• 使用梯度、近似 Hesse 矩阵定义二次函数 $$q(d) = f(x^{(k)}) + (J(x^{(k)})^T r(x^{(k)}))^T d + \frac 1 2 d^T (J(x^{(k)})^T J(x^{(k)})) d$$

• 其增量为

  $$\begin{align*} \Delta q^{(k)} & = q(d^{(k)}) - q(0) \\ & = (J(x^{(k)})^T r(x^{(k)}))^T d^{(k)} + \frac 1 2 (d^{(k)})^T (J(x^{(k)})^T J(x^{(k)})) d^{(k)} \end{align*}$$

• 目标函数增量

  $$\begin{align*} \Delta f^{(k)} & = f(x^{(k)} + d^{(k)}) - f(x^{(k)}) \\ & = f(x^{(k+1)}) - f(x^{(k)}) \end{align*}$$

• 定义$\gamma_k = \frac {\Delta f^{(k)}} {\Delta q^{(k)}}$

  • $\gamma_k$接近1说明$\Delta f^{(k)}$接近$\Delta q^{(k)}$

    • 即$f(x^{(k)} + d^{(k+1)})$接近$q(d^{(k)})$
    • 即$f(x)$在$x^{(k)}$附近接近二次函数
    • 即使用Gauss-Newton方法求解最小二乘问题效果较好
    • 即LM方法求解时$v$参数应该较小

  • $\gamma_k$接近0说明$\Delta f^{(k)}$与$\Delta q^{(k)}$ 近似程度不好

    • $d^{(k)}$不应取得过大，应减少$d^{(k)}$得模长
    • 应该增加参数$v$进行限制
    • 迭代方向趋近于负梯度方向

  • $\gamma_k$适中时，认为参数$v$选取合适，不做调整

    • 临界值通常为0.25、0.75

算法

1. 初始点 $x^{(1)}$、初始参数 $v$（小值）、精度要求 $\epsilon$，置 $k=k+1$

2. 若 $|J(x^{(k)})^T r(x^{(k)})| < \epsilon$，则停止计算，得到问题解 $x^{(k)}$，否则求解线性方程组

   $$(J(x^{(k)})^T J(x^{(k)}) + v_kI) d = -J(x^{(k)})^T r(x^{(k)})$$

   得到 $d^{(k)}$

3. 置 $x^{(k+1)} = x^{(k)} + d^{(k)}$，计算 $\gamma_k$

4. 考虑 $\gamma$

   • $\gamma < 0.25$，置$v_{k+1} = 4 v_k$
   • $\gamma > 0.75$，置$v_{k+1} = v_k / 2$
   • 否则置$v_{k+1} = v_k$

5. 置k=k+1，转2

其他问题

整形规划

整形规划：求线性函数的最值，函数包含若干整数变量，并且满足线性等式、不等式的有限约束

Unregularized Least Squares Learning Problem

$$w_T = \frac \gamma n \sum_{i=0}^{T-1} (I - \frac \gamma n {\hat X}^T \hat X)^i {\hat X}^T \hat Y$$

• $\gamma$：被引入保证 $|I - \frac \gamma n {\hat X}^T \hat X| < 1$

策略

• 考虑

  $$\min_w I_s(w) = \frac 1 {2n} \|\hat X w - \hat Y\|^2$$

• 将$w_{t+1}$带入$I_s(w)$即可证明每次迭代$I_s(w)$减小

  $$w_0 = 0 \\ w_{t+1} = (I - \frac \gamma n {\hat X}^T \hat X)w_t + \frac \gamma n {\hat X}^T \hat Y$$

正定二次目标函数

$$min f(x) = \frac 1 2 x^T G x + r^T x + \sigma$$

非线性最小二乘

$$\begin{align*} f(x) & = \frac 1 2 \sum_{i=1}^m r^2_i(x) \\ & = \frac 1 2 r(x) r^T(x) \end{align*}$$

• $r_i(x)$：通常为非线性函数
• $r(x) = (r_1(x), \cdots, r_n(x))^T$
• $x \in R^n, m \geq n$

则

$$\begin{align*} \nabla f(x) & = \sum_{i=1}^m \nabla r_i(x) r_i(x) \\ & = J(x)^T r(x) \\ \nabla^2 f(x) & = \sum_{i=1}^m \nabla r_i(x) r_i(x) + \sum_{i=1}^m r_i \nabla^2 r_i(x) \\ & = J(x)^T J(x) + \sum_{i=1}^m r_i(x) \nabla^2 r_i(x) \end{align*}$$

• $$J(x) = \begin{bmatrix} \frac {\partial r_1} {\partial x_1} & \frac {\partial r_1} {\partial x_2} & \cdots & \frac {\partial r_1} {\partial x_n} \\ \frac {\partial r_2} {\partial x_1} & \frac {\partial r_2} {\partial x_2} & \cdots & \frac {\partial r_2} {\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial r_m} {\partial x_1} & \frac {\partial r_m} {\partial x_2} & \cdots & \frac {\partial r_m} {\partial x_n} \end{bmatrix} = \begin{bmatrix} \nabla r_1(x)^T \\ \nabla r_2(x)^T \\ \vdots \\ \nabla r_m(x)^T \\ \end{bmatrix}$$ 为$r(x)$的Jacobi矩阵

Gauss-Newton法

Newton法中为简化计算，略去其Hesse矩阵中 $\sum_{i=1}^m r_i(x) \nabla^2 r_i(x)$项，即直接求解 方程组

$$J(x^{(k)})^T J(x^{(k)}) d = -J(x^{(k)})^T r(x^{(k)})$$

算法

同Newton法，仅求解Newton方程改为求解以上方程组

特点

• 实际问题中

  • 局部解$x^{ }$对应的目标函数值$f(x^{ })$接近0 时，$|r(x^{(k)})|$较小
  • 曲线$r_i(x)$接近直线， $\nabla^2 r_i(x) \approx 0$

  采用Gauss-Newton法效果较好，否则效果一般

• 矩阵$J(x^{(k)})^T J(x^{(k)})$是半正定矩阵，当Jacobi矩阵 列满秩时为正定矩阵，此时虽然$d^{(k)}$是下降方向，但仍需 类似修正牛顿法增加一维搜索策略保证目标函数值不上升

Levenberg-Marquardt方法

但$J(x^{(k)})$中各列线性相关、接近线性相关，则求解 Newton-Gauss方法中的方程组会出现困难，可以改为求解

$$(J(x^{(k)})^T J(x^{(k)}) + vI) d = -J(x^{(k)})^T r(x^{(k)})$$

• $v$：迭代过程中需要调整的参数，LM方法的关键即如何调整

定理1

• 若$d(v)$是以上方程组的解，则$|d(v)|^2$是$v$的连续下降 函数，且$v \rightarrow +\infty, |d(v)| \rightarrow 0$

• $J(x^{(k)})^T J(x^{(k)})$是对称半正定矩阵，则存在正交阵

  $$(P^{(k)})^T J(x^{(k)})^T J(x^{(k)}) P^{(k)} = \Lambda^{(k)}$$

• 则可以解出$|d(v)|^2$

• 增大$v$可以限制$|d^{(k)}|$，所以LM方法也被称为阻尼最小 二乘法

定理2

• 若$d(v)$是以上方程的解，则$d(v)$是$f(x)$在$x^{(k)}$处的 下降方向，且$v \rightarrow + \infty$时，$d(v)$的方向与 $-J(x^{(k)})^T r(x^{(k)})$方向一致

• 下降方向：$\nabla f(x^{(k)}) d(v) < 0$即可
• 方向一致：夹角余弦

• $v$充分大时，LM方法产生的搜索方向$d^{(k)}$和负梯度方向 一致

参数调整方法

使用梯度、近似Hesse矩阵定义二次函数

$$q(d) = f(x^{(k)}) + (J(x^{(k)})^T r(x^{(k)}))^T d + \frac 1 2 d^T (J(x^{(k)})^T J(x^{(k)})) d$$

• 其增量为

  $$\begin{align*} \Delta q^{(k)} & = q(d^{(k)}) - q(0) \\ & = (J(x^{(k)})^T r(x^{(k)}))^T d^{(k)} + \frac 1 2 (d^{(k)})^T (J(x^{(k)})^T J(x^{(k)})) d^{(k)} \end{align*}$$

• 目标函数增量

  $$\begin{align*} \Delta f^{(k)} & = f(x^{(k)} + d^{(k)}) - f(x^{(k)}) \\ & = f(x^{(k+1)}) - f(x^{(k)}) \end{align*}$$

• 定义$\gamma_k = \frac {\Delta f^{(k)}} {\Delta q^{(k)}}$

• $\gamma_k$接近1说明$\Delta f^{(k)}$接近$\Delta q^{(k)}$

  • 即$f(x^{(k)} + d^{(k+1)})$接近$q(d^{(k)})$
  • 即$f(x)$在$x^{(k)}$附近接近二次函数
  • 即使用Gauss-Newton方法求解最小二乘问题效果较好
  • 即LM方法求解时$v$参数应该较小

• $\gamma_k$接近0说明$\Delta f^{(k)}$与$\Delta q^{(k)}$ 近似程度不好

  • $d^{(k)}$不应取得过大，应减少$d^{(k)}$得模长
  • 应该增加参数$v$进行限制
  • 迭代方向趋近于负梯度方向

• $\gamma_k$适中时，认为参数$v$选取合适，不做调整

  • 临界值通常为0.25、0.75

算法

1. 初始点$x^{(1)}$、初始参数$v$（小值）、精度要求$\epsilon$ ，置k=k+1

2. 若$|J(x^{(k)})^T r(x^{(k)})| < \epsilon$，则停止计算， 得到问题解$x^{(k)}$，否则求解线性方程组

   $$(J(x^{(k)})^T J(x^{(k)}) + v_kI) d = -J(x^{(k)})^T r(x^{(k)})$$

   得到$d^{(k)}$

3. 置$x^{(k+1)} = x^{(k)} + d^{(k)}$，计算$\gamma_k$

4. 若

   • $\gamma < 0.25$，置$v_{k+1} = 4 v_k$
   • $\gamma > 0.75$，置$v_{k+1} = v_k / 2$
   • 否则置$v_{k+1} = v_k$

5. 置k=k+1，转2

Cone

• 锥：$C \subset V, \forall x \in C, a>0 \Rightarrow ax \in C$

  • 锥总是无界的

  • $V$：向量空间

• Convex Cone 凸锥：$\forall x,y \in C, \forall a,b > 0 \Rightarrow ax + by \in C$

  • 凸锥必然是凸集
  • 非凸锥：凸锥的补集

• Norm Cone $n$ 维标准锥：$C = { (x,t)| |x|_2 \leq t, x \in R^{n-1}, t \in R }$

• Second Order Cone 二阶锥：$C = { (x,t)|Ax+b|_2 \leq c^Tx + d }$

  • 二阶锥相对于对标准锥做了仿射变换（平移变换）

Notations and Terminology

Strong Convexity

• 凸函数 $f$ 满足

  $$\forall x, y \in R, \forall \lambda \in (0,1), f(\lambda x + (1-\lambda) y) \leq \lambda f(x) + (1-\lambda)f(y)$$

• 强凸函数：不等式严格不等的凸函数

  • 为保证强凸性，常添加二次项保证，如：增广拉格朗日

凸集相关标记

• $C \subseteq R^N$：非空凸集
• $x \in R^N$

• 点 $x \in R^N$ 到 $C$ 的距离为

  $$D_C(x) = \min_{y \in C} \|x-y\|_2$$

• 点 $x \in R^N$ 在 $C$ 上投影为

  $$P_Cx \in C, D_C(x) = \|x - P_Cx\|_2$$
  • $C \subseteq R^N$：闭凸集

• Indicator Function 凸集 $C$ 的示性函数为

  $$l_C(x) = \left \{ \begin{array} 0 & if x \in C \\ +\infty & if x \notin C \end{array} \right.$$

齐次函数

齐次函数：有倍数性质的函数，若变量乘以系数 $\alpha$，则新函数为原函数乘上 $\alpha^k$ 倍

$$f(\alpha x) = \alpha^k f(x)$$

• $\alpha \neq 0 \in F, x \in X$
• $f: X \rightarrow W$：域 $F$ 内两个向量空间之间的 $k$ 次齐次函数

• 线性函数 $f: X \rightarrow W$ 是一次齐次函数
• 多线性函数 $f: x_1 x_2 \cdots * x_n \rightarrow W$ 是 $n$ 次齐次函数

基本定理

• 欧拉定理：函数 $f: R^n \rightarrow R$ 可导、$k$ 次齐次函数，则有 $x \nabla f(x) = kf(x)$

次梯度

• 次梯度：实变量凸函数 $f$ 在点 $x_0$ 的次梯度 $c$ 满足

  $$\forall x, f(x) - f(x_0) \geq c(x - x_0)$$

• 可证明凸函数 $f$ 在 $x_0$ 处所有次梯度的集合 $\partial f(x)$ 是非空凸紧集

  • $\partial f(x) = [a, b]$，其中$a, b$为单侧极限

    $$\begin{align*} a & = lim_{x \rightarrow x_0^{-}} \frac {f(x) - f_0(x)} {x - x_0} \\ b & = lim_{x \rightarrow x_0^{+}} \frac {f(x) - f_0(x)} {x - x_0} \end{align*}$$

• 凸函数均指下凸函数，梯度不减

次梯度性质

运算性质

• 数乘性质

  $$\partial(\alpha f)(x) = \alpha \partial f(x), \alpha > 0$$

• 加法性质

  $$\begin{align*} f &= f_1 + f_2 + \cdots + f_m, \\ \partial f &= \partial f_1 + \cdots + \partial f_m \end{align*}$$

• 仿射性质：$f$为凸函数

  $$\begin{align*} h(x) &= f(Ax + b) \\ \partial h(x) &= A^T \partial f(Ax + b) \end{align*}$$

最优化性质

• 凸函数 $f$ 在点 $x_0$ 可导，当且仅当次梯度仅包含一个点，即该点导数

• 点 $x_0$ 是凸函数 $f$ 最小值，当且仅当次微分中包含 0 （此性质为“可导函数极小点导数为 0 ”推广）

• 负次梯度方向不一定是下降方向

次梯度求解

• 逐点（分段）极值的函数求次梯度
• 求出该点相应极值函数
• 求出对应梯度即为次梯度

Pointwise Maximum

逐点最大函数：目标函数为

$$\begin{align*} f(x) & = max \{f_1(x), f_2(x), \cdots, f_m(x)\} \\ I(x) & = \{i | f_i(x) = f(x)\} \end{align*}$$

• $I(x)$：保存 $x$ 处取值最大的函数下标

• 弱结果：$I(x)$ 中随机抽取，以 $f_i(x)$ 在该处梯度作为次梯度

• 强结果

  $$\partial f(x) = conv \cup_{i \in I(x)} \partial f_i(x)$$
  • 先求支撑平面，再求所有支撑平面的凸包
  • 可导情况实际上是不可导的特殊情况

分段函数

• 折点处

  $$\partial f(x) = conv\{a_i, a_{i+1}\} = [a_i, a_{i+1}]$$

• 非折点处

  $$\partial f(x) = {a_i}$$

$L_1$范数

PointWise Supremum

逐点上确界：目标函数为

$$\begin{align*} f(x) &= \sup_{\alpha \in A} f_{\alpha}(x) \\ I(x) &= \{\alpha \in A | f_{\alpha}(x) = f(x)\} \end{align*}$$

• 弱结果：可行梯度为

  $$\partial (\max_{\alpha} f_{\alpha}(x)) \in partial f(x)$$

• 强结果

  $$\partial f(x) = conv \cup_{\alpha \in I(x)} \partial f_{alpha}(x) \subseteq \partial f(x)$$

最大特征值

$$\begin{align*} f(x) & = \lambda_{max}(A(x)) = \sup_{\|y\|_2 = 1} \\ A(x) & = A_0 + x_1 A_1 + \cdots + x_n A_n \end{align*}$$

• $A_n$：对称矩阵

• 对确定 $\hat {x}$，$A(x)$ 最大特征值 $\lambda_{max}$、对应特征向量 $y$，则该点此梯度为

  $$(y^T A_0 y, \cdots, y^T A_n y)$$

Pointwise Inferior

逐点下确界：目标函数为

$$f(x) = \inf_y h(x, y)$$

• $h$：凸函数

• 弱结果：给定$x = \hat x$，可行次梯度为

  $$(\partial h(x, \hat y)|_{x=\hat x}, 0) \in \partial f(x)$$

复合函数

$$f(x) = h(f_1(x), \cdots, f_n(x))$$

• $h$：凸、不降函数
• $f_i$：凸函数

• 弱结果：给定$x = \hat x$，可行次梯度为

  $$g = z_1 g_1 + \cdots + z_k g_k \in \partial f(\hat x)$$

  • $z \in \partial h(f_1(\hat x), \cdots, f_k(\hat x))$
  • $g_i \in \partial f_i(\hat x)$

  • 证明

    $$\begin{align*} f(x) & \geq h(f_1(\hat x) + g_1^T(x - \hat x), \cdots, f_k(\hat x) + g_k^T(x - \hat x) \\ & \geq h(f_1(\hat x), \cdots, f_k(\hat x)) + z^T(g_1^T(x - \hat x), \cdots, g_k^T(x - \hat x)) \\ & = f(\hat x) + g^T(x - \hat x) \end{align*}$$

次梯度法

$$\begin{align*} x^{(k+1)} & = x^{(k)} + \alpha_k g^{(k)} \\ f_{best}^{(k+1)} & = min{f_{best}^{(k)}, f(x^{(k+1)})} \end{align*}$$

• $g^{(k)}$：函数$f$在$x^{(k)}$处次梯度

• 求解凸函数最优化的问题的一种迭代方法

• 相较于较内点法、牛顿法慢

  • 应用范围更广泛：能够用于不可微目标函数，目标函数可微时，无约束问题次梯度与梯度下降法有同样搜索方向
  • 空间复杂度更小
  • 可以和分解技术结合，得到简单分配算法
  • 通常不会产生稀疏解

步长选择

• 次梯度法选取步长方法很多，以下为保证收敛步长规则

• 恒定步长：$\alpha_k = \alpha$
• 恒定间隔：$\alpha_k = \gamma / |g^{(k)}|_2$
• 步长平方可加、步长不可加：$\sum{k=1}^{\infty} \alpha_k^2 < \infty, \sum{k=1}^{\infty} \alpha_k = \infty$
• 步长不可加、但递减：$lim_{k \rightarrow \infty} \alpha_k = 0$
• 间隔不可加、但递减：$lim_{k \rightarrow \gamma_k} \gamma_k = 0$

Hash Function

• hash：散列/哈希，将任意类型值转换为关键码值
• hash function：哈希/散列函数，从任何数据中创建小的数字“指纹”的方法
• hash value：哈希值，哈希函数产生关键码值
• collision：冲突，不同两个数据得到相同哈希值

• 哈希函数应该尽可能使得哈希值均匀分布在目标空间中
  • 降维：将高维数据映射到低维空间
  • 数据应该低维空间中尽量均匀分布

数据相关性

• Data Independent Hashing：数据无关哈希，无监督，哈希函数基于某种概率理论

  • 对原始的特征空间作均匀划分
  • 对分布不均、有趋向性的数据集时，可能会导致高密度区域哈希桶臃肿，降低索引效率

• Data Dependent Hashing：数据依赖哈希，有监督，通过学习数据集的分布从而给出较好划分的哈希函数

  • 得到针对数据密度动态划分的哈希索引
  • 破坏了传统哈希函数的数据无关性，索引不具备普适性

应用

• 查找数据结构：cs_algorithm/data_structure/hash_table
  • 哈希表
• 信息安全方向：cs_algorithm/specification/info_security
  • 文件检验
  • 数字签名
  • 鉴权协议

哈希函数

• 简单哈希函数主要用于提升查找效率（构建哈希表）

  • 要求哈希函数的降维、缩小查找空间性质
  • 计算简单、效率高

• 复杂哈希函数主要用于信息提取

  • 要求哈希函数的信息提取不可逆、非单调映射
  • 查表哈希
    • CRC 系列算法：本身不是查表，但查表是其最快实现
    • Zobrist Hashing
  • 混合哈希：利用以上各种方式
    • MD5
    • Tiger

单值输入

• 直接寻址法：取关键字、或其某个线性函数值 $hash(key) = (a * key + b) \% prime$

  • $prime$：一般为质数，以使哈希值尽量均匀分布，常用的如：$2^{32}-5$

• 数字分析法：寻找、利用数据规律构造冲突几率较小者

  • 如：生日信息前 2、3 位大体相同，冲突概率较大，优先舍去

• 平方取中法：取关键字平方后中间几位

• 折叠法：将关键字分割为位数相同部分，取其叠加和

• 随机数法：以关键字作为随机数种子生成随机值

  • 适合关键字长度不同场合

• 常用于之前哈希结果再次映射为更小范围的最终哈希值

序列输入

加法哈希

加法哈希：将输入元素相加得到哈希值

• 标准加法哈希

  1 2 3 4 5 6

  AddingHash(input): hash = 0 for ele in input: hash += ele # prime 为任意质数，常用 2^32 - 5 hash = hash % prime

  • 最终哈希结果 $\in [0, prime-1]$

位运算哈希

位运算哈希：利用位运算（移位、异或等）充分混合输入元素

• 标准旋转哈希

  1 2 3 4 5

  RotationHash(input): hash = 0 for ele in input: hash = (hash << 4) ^ (hash >> 28) ^ ele return hash % prime

• 变形 1

  1	hash = (hash<< 5) ^ (hash >> 27) ^ ele

• 变形2

  1 2 3

  hash += ele hash ^= (hash << 10) hash ^= (hash >> 6)

• 变形3

  1 2 3 4

  if (ele & 1) == 0: hash ^= (hash << 7) ^ ele ^ (hash >> 3) else: hash ^= ~((hash << 11) ^ ele ^ (hash >> 5))

• 变形4

  1	hash += (hash << 5) + ele

• 变形5

  1	hash = ele + (hash << 6) + (hash >> 16) - hash

• 变形6

  1	hash ^= (hash << 5) + ele + (hash >> 2)

乘法哈希

乘法哈希：利用乘法的不相关性

• 平方取头尾随机数生成法：效果不好

• Bernstein 算法

  1 2 3 4 5

  Bernstein(input): hash = 0 for ele in input: hash = 33 * hash + ele return hash

  • 其他常用乘数：31、131、1313、13131、131313

• 32位 FNV 算法

  1 2 3 4 5 6 7

  M_SHIFT = M_MASK = FNVHash(input): hash = 2166136261; for ele in input: hash = (hash * 16777619) ^ ele return (hash ^ (hash >> M_SHIFT)) & M_MASK

• 改进的 FNV 算法

  1 2 3 4 5 6 7 8 9 10

  FNVHash_2(input): hash = 2166136261; for ele in input: hash = (hash ^ ele) * 16777619 hash += hash << 13 hash ^= hash >> 7 hash += hash << 3 hash ^= hash >> 17 hash += hash << 5 return hash

• 乘数不固定

  1 2 3 4 5 6 7

  RSHash(input): hash = 0 a, b = 378551, 63689 for ele in input: hash = hash * a + ele a *= b return hash & 0x7FFFFFFF

• 除法也类似乘法具有不相关性，但太慢

定长序列

• 两步随机数

  1 2 3 4 5 6

  main_rand_seq = randint(k) TwoHashing(input[0,...,k]): hash = 0 from i=0 to k: hash += input[i] * main_rand_seq[i] hash = hash mod prime

Universal Hashing

• 全域哈希：键集合 $U$ 包含 $n$ 个键、哈希函数族 $H$ 中哈希函数 $h_i: U \rightarrow 0..m$，若 $H$ 满足以下则为全域哈希 $$

    \forall x \neq y \in U, | \{h|h \in H, h(x) = h(y) \} | = \frac {|H|} m
  

  $$

  • $|H|$：哈希函数集合 $H$ 中函数数量

• 独立与键值随机从中选择哈希函数，避免发生最差情况
• 可利用全域哈希构建完美哈希

性质

• 全域哈希 $H$ 中任选哈希函数 $h_i$，对任意键 $x \neq y \in U$ 冲突概率小于 $\frac 1 m$

  • 由全域哈希函数定义，显然

• 全域哈希 $H$ 中任选哈希函数 $hi$，对任意键 $x \in U$，与其冲突键数目期望为 $\frac n m$，即 $E{[collision_x]}=\frac n m$

  $$\begin{align*} E(C_x) &= E[\sum_{y \in U - \{x\}} C_{xy}] \\ &= \sum_{y \in U - \{x\}} E[C_{xy}] \\ &= \sum_{y \in U - \{x\}} \frac 1 m \\ &= \frac {n-1} m \end{align*}$$

  • $C_x$：任选哈希函数，与 $x$ 冲突的键数量
  • $C_{xy} = \left { \begin{matrix} 1, & h_i(x) = h_i(y) \ 0, & otherwise \end{matrix} \right.$：指示 $x,y$ 是否冲突的指示变量

  • $m = n^2$ 时，冲突期望小于 0.5
    • $n$ 个键两两组合数目为 $C_n^2$
    • 则 $E_{total} < C_n^2 \frac 1 n < 0.5$

例

• 以下构造 $[0,p-1] \rightarrow [0,m-1]$ 全域哈希

• $p$ 为足够大素数使得所有键值 $\in [0,p-1]$

  • 记 $Z_p = { 0,1,\cdots,p-1 }$
  • 记 $Z_p^{*}={ 1,2,\cdots,p-1 }$
  • 且哈希函数映射上限（哈希表长度） $m < max(U) < p$

• 记哈希函数

  $$\forall a \in Z_p^{*}, b \in Z_p, h_{a, b}(k) = ((a k + b) \% p) \% m$$

• 则以下哈希函数族即为全域哈希

  $$H_{p,m} = {h_{a,b}|a \in Z_p^{*}, b \in Z_p}$$

Locality Sensitive Hashing

LSH：局部敏感哈希

• $(r_1,r_2,P_1,P_2)-sensitive$ 哈希函数族 $H$ 需满足如下条件 $$ \begin{align*}

    Pr_{H}[h(v) = h(q)] \geq P_1, & \forall q \in B(v, r_1) \\
    Pr_{H}[h(v) = h(q)] \geq P_2, & \forall q \notin B(v, r_2) \\
  

  \end{align*}$$

  • $h \in H$
  • $r_1 < r_2, P_1 > P_2$：函数族有效的条件
  • $B(v, r)$：点 $v$ 的 $r$ 邻域
  • $r_1, r_2$：距离，强调比例时会表示为 $r_1 = R, r_2 = cR$

• 此时 相似目标（距离小）有更大概率发生冲突

LSH查找

思想

• 相似目标更有可能映射到相同哈希桶中

  • 则只需要在目标所属的哈希桶中进行比较、查找即可
  • 无需和全集数据比较，大大缩小查找空间

• 可视为降维查找方法

  • 将高维空间数据映射到 1 维空间，寻找可能近邻的数据点
  • 缩小范围后再进行精确比较

概率放大

• 期望放大局部敏感哈希函数族 $Pr_1, Pr_2$ 之间差距

• 增加哈希值长度（级联哈希函数中基本哈希函数数量） $k$

  • 每个哈希函数独立选择，则对每个级联哈希函数 $g_i$ 有 $Pr[g_i(v) = g_i(q)] \geq P_1^k$
  • 虽然增加哈希键位长会减小目标和近邻碰撞的概率，但同时也更大程度上减少了和非近邻碰撞的概率、减少搜索空间

  • 级联哈希函数返回向量，需要对其再做哈希映射为标量，方便查找

• 增加级联哈希函数数量（哈希表数量） $L$

  • $L$个哈希表中候选项包含真实近邻概率 至少 为 $1 - (1 - P_1^k)^L$
  • 增加哈希表数量能有效增加候选集包含近邻可能性
  • 但同时也会增大搜索空间

搜索近似最近邻

• 使用 $L$ 个级联哈希函数分别处理待搜索目标
• 在 $L$ 个哈希表分别寻找落入相同哈希桶个体作为候选项
• 在所有候选项中线性搜索近邻

基于汉明距离的 LSH

• 在汉明距离空间中搜索近邻
  • 要求数据为二进制表示
  • 其他距离需要嵌入汉明距离空间才能使用
    • 欧几里得距离没有直接嵌入汉明空间的方法
      • 一般假设欧几里得距离和曼哈顿距离差别不大
      • 直接使用对曼哈顿距离保距嵌入方式

设计哈希函数族

• 考虑哈希函数族 $H = { h_1, h_2, \cdots, h_m }$

  • 其中函数 $h_i$ 为 ${0, 1}^d$ 到 ${0, 1}$ 的映射：随机返回特定比特位上的值

• 从 $H$ 中随机的选择哈希函数 $h_i$

  • 则 $Pr[h_i(v) = h_i(q)]$ 等于 $v, q$ 相同比特数比例，则
    • $Pr_1 = 1 - \frac R d$
    • $Pr_2 = 1 - \frac {cR} d$
  • 考虑到 $Pr_1 > Pr_2$，即此哈希函数族是局部敏感的

基于 Jaccard 系数的 LSH

• 考虑 $M * N$ 矩阵 $A$，元素为 0、1

  • 其中
    • $M$：集合元素数量
    • $N$：需要比较的集合数量
  • 目标：寻找相似集合，即矩阵中相似列

• 用 Jaccard 系数代表集合间相似距离，用于搜索近邻

  • 要求各数据向量元素仅包含 0、1：表示集合是否包含该元素

定义 Min-hashing 函数族

• 对矩阵 $A$ 进行 行随机重排 $\pi$，定义 Min-hashing 如下

  $$h_{\pi}(C) = \min \pi(C)$$

  • $C$：列，表示带比较集合
  • $\min \pi(C)$：$\pi$ 重排矩阵中 $C$ 列中首个 1 所在行数

• 则不同列（集合） Min-hashing 相等概率等于二者 Jaccard 系数

  $$\begin{align*} Pr(h_{\pi}(C_1) = h_{\pi}(C_2)) & = \frac a {a + b} \\ & = Jaccard_d(C_1, C_2) \end{align*}$$

  • $a$：列 $C_1, C_2$ 取值均为 1 的行数
  • $b$：列 $C_1, C_2$ 中仅有一者取值为 1 的行数
  • 根据 Min-hashing 定义，不同列均取 0 行被忽略

Min-hashing 实现

• 数据量过大时，对行随机重排仍然非常耗时，考虑使用哈希函数模拟行随机重排

  • 每个哈希函数对应一次随机重排
    • 哈希函数视为线性变换
    • 然后用哈希函数结果对总行数取模
  • 原行号经过哈希函数映射即为新行号

• 为减少遍历数据次数，考虑使用迭代方法求解

  1 2 3 4 5 6

  for i from 0 to N-1: for j from 0 to M-1: if D[i][j] == 1: for k from 1 to K: # 更新随机重拍后，第 `j` 列首个 1 位置 DD[k][j] = min(h_k(i), DD[k][j])

  • $D$：原始数据特征矩阵
  • $DD$：$Min-hashing* 签名矩阵
  • $N$：特征数量，原始特征矩阵行数
  • $M$：集合数量，原始特征矩阵列数
  • $K$：模拟的随机重排次数，Min-hashing 签名矩阵行数
  • $h_k,k=1,…,K$：$K$ 个模拟随机重排的哈希函数，如 $h(x) = (2x + 7) mod N$

  • 初始化 Min-hashing 签名矩阵所有值为 $\infty$
  • 遍历 $N$ 个特征、$M$ 个集合
    • 查看每个对应元素是否为 1
    • 若元素为 1，则分别使用 $K$ 个哈希函数计算模拟重排后对应的行数
    • 若计算出行数小于当前 *Min-hash$ 签名矩阵相应哈希函数、集合对应行数，更新
  • 遍历一遍原始数据之后即得到所有模拟重排的签名矩阵

Exact Euclidean LSH

• $E^2LSH$：欧式局部LSH，LSH Based-on P-stable Distribution

  • 使用内积将向量随机映射到哈希值
  • p-stable 分布性质将欧式距离同哈希值相联系，实现局部敏感

• $E^2LSH$ 特点

  • 基于概率模型生成索引编码结果不稳定
  • 随编码位数 $k$ 增加的，准确率提升缓慢
  • 级联哈希函数数量 $L$ 较多时，需要大量存储空间，不适合大规模数据索引

p-stable 哈希函数族

$$h_{a, b}(v) = \lfloor \frac {av + b} r \rfloor$$

• $v$：$n$ 维特征向量
• $a = (X_1,X_2,\cdots,X_n)$：其中分量为独立同 p-stable 分布的随机变量
• $b \in [0, r]$：均匀分布随机变量

p-stable 哈希函数碰撞概率

• 考虑$|v_1 - v_2|_p = c$的两个样本碰撞概率

• 显然，仅在 $|av1 - av_2| \leq r$ 时，才存在合适的 $b$ 使得 $h{a,b}(v1) = h{a,b}(v_2)$

  • 即两个样本碰撞，不失一般性可设 $av_1 \leq av_2$
  • 此 $r$ 即代表局部敏感的 局部范围

• 若 $(k-1)r \leq av_1 \leq av_2 < kr$，即两个样本与 $a$ 内积在同一分段内

  • 易得满足条件的 $b \in [0,kr-av_2) \cup [kr-av_1, r]$
  • 即随机变量 $b$ 取值合适的概率为 $1 - \frac {av_2 - av_1} r$

• 若 $(k-1)r \leq av_1 \leq kr \leq av_2$，即两个样本 $a$ 在相邻分段内

  • 易得满足条件的 $b \in [kr-av_1, (k+1)r-av_2)$
  • 即随机变量 $b$ 取值合适的概率同样为 $1 - \frac {av_2 - av_1} r$

• 考虑 $av_2 - av_1$ 分布为 $cX$，则两样本碰撞概率为

  $$\begin{align*} p(c) & = Pr_{a,b}(h_{a,b}(v_1) = h_{a,b}(v_2)) \\ & = \int_0^r \frac 1 c f_p(\frac t c)(1 - \frac t r)dt \end{align*}$$

  • $c = |v_1 - v_2|_p$：特征向量之间$L_p$范数距离
  • $t = a(v_1 - v_2)$
  • $f$：p稳定分布的概率密度函数

  • $p=1$ 柯西分布

    $$p(c) = 2 \frac {tan^{-1}(r/c)} \pi - \frac 1 {\pi(r/c)} ln(1 + (r/c)^2)$$

  • $p=2$ 正态分布

    $$p(c) = 1 - 2norm(-r/c) - \frac 2 {\sqrt{2\pi} r/c} (1 - e^{-(r^2/2c^2)})$$

性质、实现

限制近邻碰撞概率

• $r$ 最优值取决于数据集、查询点

  • 根据文献，建议$r = 4$

• 若要求近邻 $v \in B(q,R)$以不小于$1-\sigma$ 概率碰撞，则有

  $$\begin{align*} 1 - (1 - p(R)^k)^L & \geq 1 - \sigma \\ \Rightarrow L & \geq \frac {log \sigma} {log(1 - p(R)^k)} \end{align*}$$

  则可取

  $$L = \lceil \frac {log \sigma} {log(1-p(R)^k)} \rceil$$

• $k$ 最优值是使得 $T_g + T_c$ 最小者

  • $T_g = O(dkL)$：建表时间复杂度
  • $T_c = O(d |collisions|)$：精确搜索时间复杂度
  • $T_g$、$T_c$ 随着 $k$ 增大而增大、减小

• 具体实现参考https://www.mit.edu/~andoni/LSH/manual.pdf

限制搜索空间

• 哈希表数量 $L$ 较多时，所有碰撞样本数量可能非常大，考虑只选择 $3L$ 个样本点

• 此时每个哈希键位长 $k$、哈希表数量 $L$ 保证以下条件，则算法正确

  • 若存在 $v^{ }$ 距离待检索点 $q$ 距离小于 $r_1$，则存在 $g_j(v^{ }) = g_j(q)$

  • 与 $q$ 距离大于 $r_2$、可能和 $q$ 碰撞的点的数量小于 $3L$

    $$\sum_{j=1}^L |(P-B(q,r_2)) \cap g_j^{-1}(g_j(q))| < 3L$$

• 可以证明，$k, L$ 取以下值时，以上两个条件以常数概率成立 （此性质是局部敏感函数性质，不要求是 $E^2LSH$）

  $$\begin{align*} k & = log_{1/p_2} n\\ L & = n^{\rho} \\ \rho & = \frac {ln 1/p_1} {ln 1/p_2} \end{align*}$$

• $\rho$ 对算法效率起决定性作用，且有以下定理

  • 距离尺度 $D$ 下，若 $H$ 为 $(R,cR,p1,p_2)$-敏感哈希函数族，则存在适合 (R,c)-NN 的算法，其空间复杂度为 $O(dn + n^{1+\rho})$、查询时间为 $O(n^{\rho})$ 倍距离计算、哈希函数计算为 $O(n^{\rho} log{1/p_2}n)$， 其中 $\rho = \frac {ln 1/p_1} {ln 1/p_2}$

  • $r$ 足够大、充分远离 0 时，$\rho$ 对其不是很敏感
  • $p1, p_2$ 随 $r$ 增大而增大，而 $k = log{1/p_2} n$ 也随之增大，所以 $r$ 不能取过大值

Scalable LSH

Scalable LSH：可扩展的 LSH

• 对动态变化的数据集，固定哈希编码的局部敏感哈希方法对数据 动态支持性有限，无法很好的适应数据集动态变化

  • 受限于初始数据集分布特性，无法持续保证有效性
  • 虽然在原理上支持数据集动态变化，但若数据集大小发生较大变化，则其相应哈希参数（如哈希编码长度）等需要随之调整，需要从新索引整个数据库

• 在 $E^2LSH$ 基础上通过 动态增强哈希键长，增强哈希函数区分能力，实现可扩展 LSH

混淆矩阵

• 对比实际类别值、预测类别值，编制混淆矩阵
• 基于混淆矩阵，计算各类错判率、总错判率（总错判率会受到数据不平衡性的影响）

F-Measure

F-测度：准率率和召回率综合值，越大越好

$$F-measure = \frac {(\beta^2 + 1) * P * R} {\beta^2 * P + R}$$

• $P = \frac {TP} {TP+FP}$：查准率、精确率
• $R = \frac {TP} {TP+FN}$：查全率、召回率、覆盖率

F1 值

F1值：$\beta=1$ 时的 F测度

$$\begin{align*} \frac {1} {F_{1}} &= \frac {1} {2} \left( \frac {1} {P} + \frac {1} {R} \right) \\ \Rightarrow F_{1} &= \frac {2 * P * R} {P + R} = \frac {2 * TP} {样例总数 + TP - TN} \end{align*}$$

TPR、FPR

• TPR、FPR 可视为对 TP、FP 用样本数量归一化的结果

  • 样本全体中正、负样本数量往往差距很大，直接比较 TP、FP 不合理
  • 考虑使用样本正、负数量归一化，即计算正比例 TPR、负比例 FPR

• TPR 越高越好，FPR 越低越好，但是这两个指标相互制约，两者同时增加、减小

  • 模型倾向于将样本 判定为 为正例，则 TP、FP 同时增加，TPR、FPR 同时变大
  • 即模型取不同阈值，会产生正相关的 TPR、FPR 的点列

Recevier Operating Characteristic Curve

ROC 曲线：不同 正样本概率 划分阈值下 TPR、FPR 绘制的折线/曲线

$$TPR = \frac {TP} {TP+FN} \\ FPR = \frac {FP} {FP+TN}$$

• ROC 曲线即以 FPR 为横坐标、TPR 为正坐标绘制曲线

  • FPR 接近 1 时，TPR 也接近 1，这是不可避免的
  • 而 FPR 接近 0 时，TPR 越大越好
  • 所以模型 ROC 曲线下方面积越大，模型判断正确效果越好

• 理解

  • 将正负样本的正样本概率值分别绘制在 x=1、x=-1 两条直线上
  • 阈值即为 y=threshold 直线
  • TPR、FPR 则为 x=1、x=-1 两条直线在阈值直线上方点数量，与各直线上所有点数量比值

Accuracy

准确率、误分率：评价分类器性能一般指标

$$\begin{align*} acc & = \frac 1 N sign(y_i = \hat y_i) \\ & = \frac {TP+TN} N \\ mis & = 1 - acc \end{align*}$$

• $y_i$：第 $i$ 样本实际类别
• $\hat y_i$：第 $i$ 样本预测类别
• $N$：样本数量

• 对给定测试集，分类器正确分类样本数与总样本数比值
• 即 0-1 损失函数时经验风险

Top PR

头部准召：评估模型头部性能

$$pr_{top} = \frac {TP_{top}} {TOP}$$

• $TOP$：指定的头部数量
• $TP_{top}$：头部中正例数量（正例指已知原 $TOP$ 样本）

Area Under Curve

AUC 值：ROC 曲线下方面积，越大越好

• AUC 值实际含义：随机抽取一对正、负样本，对其中正样本的正样本预测概率值、大于负样本的正样本预测概率值的概率

  • $=1$：完美预测，存在一个阈值可以让模型 TPR 为 1，FPR 为 0
  • $(0.5, 1)$ ：优于随机预测，至少存在某个阈值，模型 $TPR > FPR$
  • $=0.5$：同随机预测，无价值
  • $[0, 0.5)$：差于随机预测，但是可以反向取预测值

AUC 计算

• 绘制 ROC 曲线，计算曲线下面积

  • 给定一系列阈值（最精确时为样本数量），分别计算 TPR、FPR
  • 根据 TPR、FPR 计算 AUC

• 正负样本分别配对，计算正样本预测概率大于负样本比例

  $$\begin{align*} auc & = \frac {\sum I(P_P > P_N)} {M * N} \\ I(P_P, P_N) & = \left \{ \begin{array}{l} 1, & P_P > P_N, \\ 0.5, & P_P = P_N, \\ 0, & P_P < P_N \end{array} \right. \end{align*}$$

  • $M, N$：正、负样本数量

• Mann-Witney U 检验：即正、负样本分别配对的简化公式

  $$auc = \frac {\sum_{i \in Pos} rank(i) - \frac {M * (M+1)} 2} {M * N}$$

  • $Pos$：正样本集合
  • $rank(i)$：样本 $i$ 的按正样本概率排序的秩（对正样本概率值相同样本，应将秩加和求平均保证其秩相等）

Weighted-AUC

WAUC：给 每个样本 赋权，计算统计量时考虑样本权重

• FPR、TPR 绘图

  $$\begin{align*} WTPR & = \frac {\sum_{i \in Pos} w_i I(\hat y_i=1)} {\sum_{i \in Pos} w_i} \\ WFPR & = \frac {\sum_{j \in Neg} w_j I(\hat y_j=1)} {\sum_{j \in Neg} w_j} \end{align*}$$

  • $WTPR, WFPR$：加权 TPR、加权 FPR
  • $\hat y_i$：样本预测类别
  • $w_i$：样本权重

• Mann-Witney U 检验：考虑其意义，带入权重即可得

  $$\begin{align*} auc = \frac {\sum_{i \in Pos} w_i * rank(i) - \sum_{i \in Pos} w_i * rank_{pos}(i)} {\sum_{i \in Pos} w_i * \sum_{j \in Neg} w_j} \end{align*}$$

  • $rank_{pos}(i)$：正样本内部排序，样本$i$秩
  • $Neg$：负样本集合

多分类 AUC

• Micro-AUC：将每个类别视为样本标签，计算全体样本的正标签、负标签的 AUC

  • $n$ 个样本的 $m$ 维标签展平， 则其中有 $n$ 个正样本、$n * (m-1)$ 个负样本
  • $n$ 个样本的 $m$ 个分类器共 $n * m$ 个得分展平
  • 使用以上预测得分、标签计算 AUC

  1 2 3 4 5 6 7 8 9 10

  # one-vs-rest分类器得分 y_score = classifer.transform(X_test) # 展平后计算fpr、tpr fpr_micro, tpr_micro, threshhold_micro = \ skilearn.metrics.roc_curve(y_test.ravel(), y_score.ravel()) # 利用fpr、tpr计算auc auc_micro = skilearn.metrics.auc(fpr_micro, tpr_micro) # 等价于直接调用 auc_micro = skilearn.metrics.roc_auc_score(y_test, y_score, average="micro")

• Macro-AUC：对各类别，分别以计算 ROC 曲线（即 TPR、FPR），计算平均 ROC 曲线得到 AUC

  • 对各类别分别计算 TPR、FPR，共 $m$ 组 TPR、FPR

  • 平均合并 TPR、FPR，计算 AUC

    • 方法1：合并 FPR、去除重复值，使用 $m$ 组 TPR、FPR 分别求合并后 FPR 插值

      1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

      # 分别计算各类别fpr、tpr fprs, tprs = [0] * n_classes, [0] * n_classes for idx in range(n_classes): fprs[idx], tprs[idx], _ = sklearn.metrics.ruc_curve( y_test[:, i], y_score[:, i]) # 合并fpr all_fpr = np.unique(np.concatenate(fprs)) mean_tpr = np.zeros_like(all_fpr) # 计算合并后fpr插值 for idx in range(n_classes): mean_tpr += scipy.interp(all_fpr, fpr[idx], tpr[idx]) mean_tpr /= n_classes auc_macro = sklearn.metrics.auc(all_fpr, mean_tpr) # 但是和以下结果不同 auc_macro = sklearn.metrics.roc_auc_score(fprs)

• 以上分类器均为 one-vs-rest 分类器，$m$ 个类别则 $m$ 个分类器、每个样本 $m$ 个得分

Kolmogorov-Smirnov 统计量

KS 值：刻画区分正负样本能力

$$KS = max \{|TPR - FPR|\}$$

• KS 值体现 最理想情况 下，对正负样本区分能力
  • 即 ROC 曲线与 $TPR = FPR$ 直线的最远距离

Squared Error

Mean Squared Error

MSE：均方误差（偏差）

$$MSE = \frac 1 n \sum_{i=1}^{n} (y_{i} - \hat{y_{i}})^{2}$$

Mean Absolute Error

MAE：平均绝对误差

$$MAE = \frac 1 n \sum_{i=1}^n |y_i - \hat {y_i}|$$

Mean Absolute Percentage Error

MAPE：平均绝对百分比误差

$$MAPE = \frac 1 n \sum_{i=1}^n |\frac {y_i - \hat {y_i}} {y_i}|$$

Symmetric Mean Absolute Percentage Error

SMAPE：对称平均绝对百分比误差

$$MAPE = \frac 1 n \sum_{i=1}^n |\frac {y_i - \hat {y_i}} {(|y_i| + |\hat {y_i}|) / 2}|$$

$R^2$

$$\begin{align*} R^2 & = 1 - \frac {SSE} {SST} = \frac {SSR} {SST} \\ R^2_{adj} & = 1 - \frac {1 - R^2} {n - p - 1} \end{align*}$$

• $n, p$：样本量、特征数量
• $SSE$：残差平方和
• $SSR$：回归平方和、组内平方和
• $SST$：离差平方和
• $R^2_{adj}$：调整的$R^2$

Akaike Information Criterion

AIC ：赤池信息准则

$$\begin{align*} AIC & = -2log(L(\hat \theta, x)) + 2p \\ & = nln(SSE/n) + 2p \end{align*}$$

• $n, p$：样本量、特征数量
• $\theta$：带估参数
• $L(\theta, x)$：似然函数
• $SSE$：残差平方和

Bayesian Information Criterion

BIC：贝叶斯信息准则

$$\begin{align*} BIC & = -2log(L(\hat \theta, x)) + ln(n)p \\ & = nln(SSE/n) + ln(n)p \end{align*}$$

$C_p$

$$\begin{align*} C_p & = \frac {SSE} {\hat {\sigma^2}} - n + 2p \\ & = (n - m - 1) \frac {SSE_p} {SSE_m} - n + 2p \end{align*}$$

• $p$：选模型特征子集中特征数量
• $m$：所有特征数量
• $SSE_p$：选模型中残差平方和
• $SSE_m$：全模型中残差平方和