Posted Updated Algorithm / Data Structure31 minutes read (About 4716 words)0 visits

查找/搜索树

总述

  • 二叉查找树：最基础的查找树，但是不平衡时效率很差
  • 自平衡查找树：使用旋转技术得到平衡二叉树
  • 多路查找树：使用多叉树达到平衡
  • 树高度一般即决定其查找、插入、删除效率
  • 以代码复杂性、插入节点时间代价，换取查询时$logN$性能

Self-Balancing Binary Tree

自平衡查找树：如果节点插入、删除产生了一棵违背平衡要求的树， 就从称为旋转的一系列特定变换中选择一种，重新构造树使得 树满足平衡要求

  • 不同的对平衡的定义产生了不同的实现
  • 这种方案属于变治法中实例化简

Balance Factor

平衡因子：节点左、右子树高度差（一般右树-左数）

  • AVL树中平衡情况下节点平衡因子只能为-1、+1、0

  • 更新节点后可能存在不平衡节点，其平衡因子可能变为-2、+2

  • 平衡因子也可以被定义为左右子树叶子数

Rotation

旋转需要使得二叉树平衡时，保证二叉树依然有序

  • 左旋：节点平衡因子符号为正，即右子树高于左子树

    • 节点T下沉为其右儿子R的左儿子
    • 如果右儿子R本身有左子树RL，则左子树RL成为节点T 新右子树

  • 右旋：节点平衡因子符号为负，即左子树高于右子树，

    • 节点T下沉为其左儿子L的右儿子
    • 如果左儿子L本身有右子树LR，则右子树LR成为节点T 新左子树
  • 旋转只涉参与选择的至多3个节点指针变化，其余节点状态保持
  • “旋转”行为确实类似：节点绕其子节点旋转，子节点旋转后上浮 成为父节点
  • 参与旋转的两个节点也称为轴

分类

  • AVL树
  • 红黑树
  • 分裂树

Multiway Search Tree

多路查找树：允许查找树中单个节点中不止包含一个元素

  • 二叉查找树的推广，用于磁盘超大数据集的高效存取
  • 此方案属于变治法中改变表现

分类

  • 2-3树
  • 2-4树
  • B树
  • B+树

Binary Search Tree

二叉查找树：分配给每个父母顶点的数字都比其左子树中数字大， 比右子树数字小

  • 二叉树有序，保证二叉树能够快速找到中间元素，从而支持 二分查找

特点

  • 对于n个顶点的二叉树，满足 $ \lfloor {log_{2}^{n}} \rfloor \leq h \leq n-1 $

  • 二叉查找树的查找算法效率取决于二叉树的高度

    • 平均情况下，查找、插入、删除时间$\in Theta(logn)$

    • 最差情况下（严重不平衡的树，接近链表结构），树高度 h接近节点数n，查找、插入、删除时间$\in Theta(n)$

  • 包含n个键的二叉查找树总数量 $c(n) = \frac 1 {n+1} C_{2n}^n, c(0)=1$

应用

  • 查找

操作

查找

在给定二叉查找树中查找给定键值K

  • 如果树为空，查找失败

  • 若树不为空，将查找键K和树根节点K(r)比较

    • 相等则查找停止
    • $K < K(r)$：在左子树中继续查找
    • $K > K(r)$：在右子树中继续查找
特点
  • 算法时间效率
    • 最差情况下，二叉树完全偏斜，需要进行n次比较
    • 随机情况下，查找n个随机键构造的二叉树比较次数$2logn$

插入

除非是空树，否则总是把新键K插入叶子节点中

  • 通过查找K确定合适插入位置（叶子节点）
  • 若K大于叶子节点键值，则作为右子女，否则作为左子女

最优二叉查找树

对集合中元素确定的查找概率，成功查找的平均比较次数最小的 二叉查找树（可以扩展到包含不成功查找）

  • $a_i, i=1,2,\cdots,n$：从小到大互不相等的键
  • $p_i, i=1,2,\cdots,n$：键查找概率
  • $T_i^j$：由键$a_i, \cdots, a_j$构成的二叉树
  • $C(i, j)$：成功查找的最小平均查找次数

动态规划构造

  • 根据最优化法则，最优二叉查找树左右子树均是最优排列的

  • 二叉树$Ti^j$有序，设树根为$a_1$，$a_2,..,a{k-1}$构成 的左子树、$a_{k+1},..,a_j$构成右子树均是最优排列的

递推式如下

  • $1 \leqslant i \leqslant j \leqslant n$

  • $1 \leqslant i \leqslant n+1, C(i, i-1)=0$：空树

  • $1 \leqslant i \leqslant n, C(i, i)=p_i$：单节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
OptimalBST(P[1..n])
	// 动态规划法构建最优二叉查找树
	// 输入：P[1..n]n个键查找概率
	// 输出：在最优BST中查找成功的平均比较次数，最优BST子树根表
	for i = 1 to n do
		C[i, i-1] = 0
		C[i, i] = P[i]
		R[i, i] = i
	C[n+1, n] = 0
		// 初始化平均查找次数表、子树根表
	for d = 1 to n-1 do
		// d为二叉树节点数
		for i = 1 to n-d do
			// n-d是为了控制j的取值
			j = i + d
			minval = \infty
			for k = i to j do
				// 遍历设置二叉树根节点
				if C[i, k-1] + C[k+1, j] < minval
					minval = C[i, k-1] + C[k+1, j]
					kmin = k
			R[i, j] = kmin
			sum = P[i]
			for s=i+1 to j do
				sum += P[s]
			C[i, j] = minval + sum
	return C[1, n], R

算法特点

  • 算法效率
    • 算法时间效率为立方级
    • 算法空间效率为平方级

AVL Tree

AVL树：要求其节点在左右子树高度差不能超过1的平衡二叉树

  • 基本思想：总能通过一次简单的节点重排使树达到平衡

    • 如果树插入操作使得一棵AVL树失去平衡，利用旋转对树作 变换
    • 若有多个这样的节点，找出最靠近新插入的叶子节点不平衡 结点，然后旋转以该节点为根的子树

  • AVL树高度h即为其查找、插入效率

    • 包含n个节点AVL树高度h满足 $\lfloor log_2 n \rfloor \leq h < 1.4405log_2(n+2) - 1.3277$

    • 最差情况下，操作效率$\in \Theta(logn)$

    • 平均而言，在n不是太小时，高度h平均为 $1.01log_2 n + 0.1$（几乎同折半查找有序数组）

  • AVL树缺点（平衡代价），阻碍AVL树成为实现字典的标准结构

    • 需要频繁旋转
    • 维护树的节点平衡
    • 总体比较复杂

旋转

按照节点平衡符号进行旋转：+左旋、-右旋

  • 单旋：不平衡节点、不平衡子节点不平衡因子符号相同

    • 全为+：不平衡节点左旋
    • 全为-：不平衡节点右旋

  • 双旋：不平衡节点、不平衡子节点不平衡因子符号不同

    • 先旋转不平衡子节点
    • 再旋转不平衡节点
  • 优先考虑最底层、不平衡节点

插入节点

AVL树插入关键：查找不平衡节点

  • 节点中应有存储其平衡因子的实例变量
  • 插入过程中经过每个节点返回当前节点子树深度是否变化
  • 比较节点平衡因子、子节点深度变化返回值判断是否平衡
  • 插入过程中查询的每个节点都有可能不平衡
  • 自下而上返回深度变化情况，优先旋转最底层不平衡节点

4种插入情况

根据插入情况的不同，对最靠近新插入叶子节点的不平衡点T

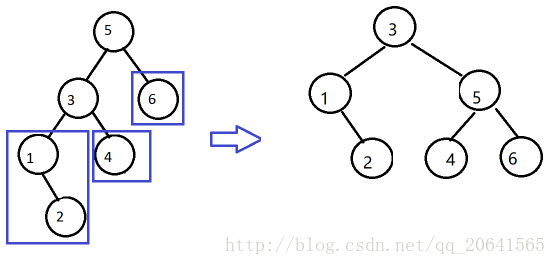
LL

插入T左儿子L的左子树LL：平衡因子全-

  • 即T到最底层叶节点（只可能有一个）的路径为LL（中间省略）
  • R-rotation：右单转，对T做一次右旋即可平衡

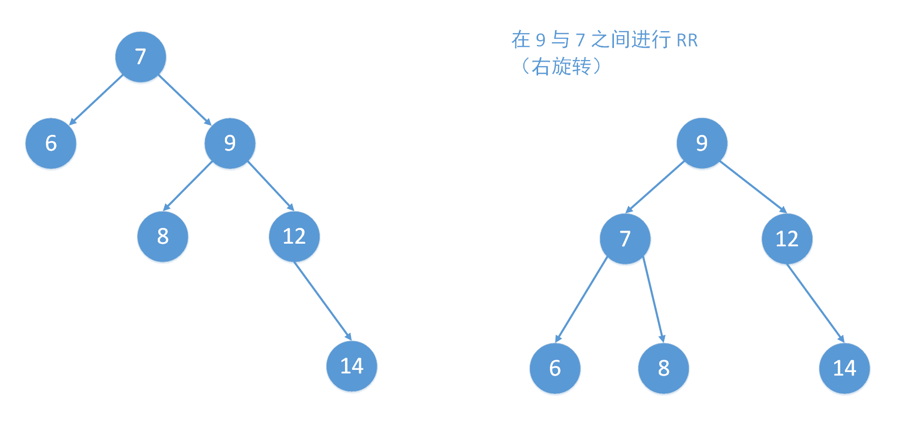
avl_ll_rotation

RR

插入T右儿子R的右子树R：平衡因子全+

  • 即T到最底层叶节点（只可能有一个）的路径为RR（中间省略）
  • L-rotation：左单转，对T做一次左旋即可平衡

avl_ll_rotation

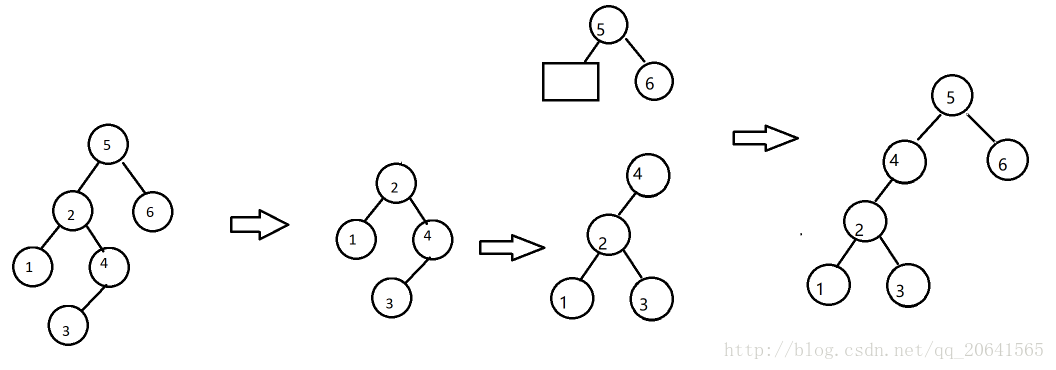
LR

插入T左儿子L的右子树R：平衡因子-+

  • 即T到最底层叶节点（只可能有一个）的路径为LR（中间省略）
  • LR-rotation：左右双转
    • 先对左儿子L做一次左旋，变成LL模式
    • 在LL模式下，再对T做一次右旋

avl_lr_rotation

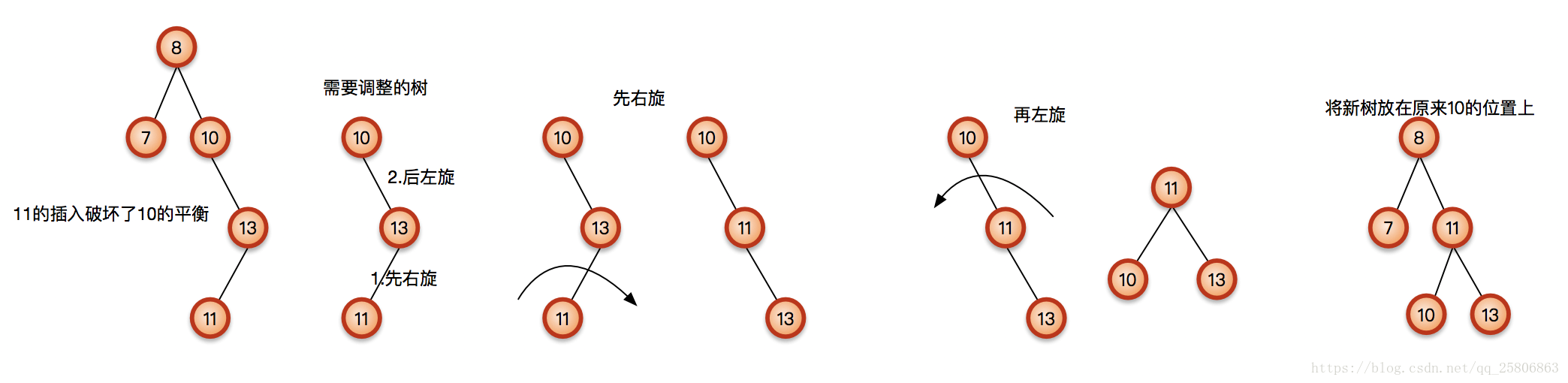
RL

插入T右儿子R的左子树L：平衡因子+-

  • 即T到最底层叶节点（只可能有一个）的路径为RL（中间省略）
  • RL-rotation：右左双转
    • 先对右儿子R做一次右旋，变成RR模式
    • 在RR模式下，再对T做一次左旋

avl_rl_rotation

实现

删除节点

  • 在AVL树中删除键相对而言比较困难，但也是对数级的

实现

Red-Black Tree

红黑树：能够容忍同一节点的一棵子树高度是另一棵的2倍

Splay Tree

分裂树：

2-3树

2-3树：可以包含两种类型的节点2节点、3节点，树的所有叶子节点 必须位于同一层

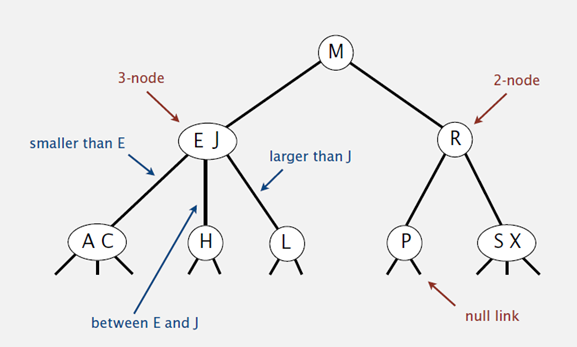
2_3_tree

  • 2-3树的高度即决定其查找、插入、删除效率

    • 节点数为n的2-3数高度h满足 $log_3(n+1)-1 \leq h \leq log_2(n+1) - 1$
    • 最差、平均情况下，操作效率$\in \Theta(logn)$

  • 2-3树总是高度平衡

    • 所有叶子节点位于同一层，即树根到其路径长度相同
    • 2-3树平衡代价
      • 树中节点可以有1或2个键，需要处理2种节点类型
      • 拆分3节点的情况有很多种

  • 节点类型

    • 2节点：只包含1个键K、2个子女

      • 左子女：作为所有键都小于K的子树的根
      • 右子女：作为所有键都大于K的子树的根

    • 3节点：两个有序键$K_1 < K_2$、3个子女

      • 最左边子女：作为键值小于$K_1$的子树的根
      • 中间子女：作为键值位于$[K_1, K_2]$之间子树的根
      • 最右边子女：作为键值大于$K_2$的子树的根
  • 类似的还有2-4树

查找

  • 如果根是2节点，当作二叉树查找

    • 若K等于根键值，停止
    • 若K小、大于根键值，在左、右子树中查找

  • 若根是3节点

    • 和两个键值比较，有相等，停止
    • 否则能确定应该在3棵子树中哪棵继续查找

插入节点

除非是空树，否则总是把新键K插入叶子节点中

  • 查找K确定合适的插入位置（叶子节点）

  • 若叶子节点2节点，根据大小关系将K作为第一个键或第二个键 插入 2_3_2node_insert

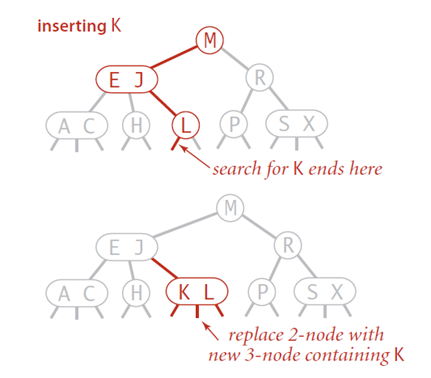
  • 若叶子节点3节点，把叶子分裂为两个节点：3个键中最小的放入 第一个叶子中，最大的放入第二个叶子中，中间的键提升到原 叶子节点父母中

    2_3_3node_insert

    • 若叶子就是根，则需要创建新根容纳中间键
    • 中间键的提升可能会导致父母节点分裂，并引起祖先链条上 多个节点的分裂

删除节点

B树

B树：允许节点可以有$1~m-1$个键（$2~m$个子女）

1
2
3
4
5
6
7
#define BTREE_M
typedef struct BTNode{
	unsigned int degree;				// 节点实际包含键数
	KeyType key_slots[BTREE_M-1];		// 节点存储键数组
	struct BTNode ptr_slots[BTREE_M];	// 指向子女节点指针
	struct BTNode * ptr_parent;			// 父节点指针
}BTNode, *BTNodePtr;
  • $m$：B树阶数，节点允许最大子女数
    • 节点最多允许有$m-1$个条目
    • $m=2$即为二叉树、$m=3$即为2-3树
  • 键：用于构建树的关键字，和具体条目类似于键值对

  • 根节点具有$2~m$个子女，除非为叶子节点

  • 非根、非叶节点具有$[\lceil m/2 \rceil, m]$个子女

    • 即具有$[\lceil m/2 \rceil - 1, m]$个有序键

    • 其中子树$T_0$所有键小于$K_1$，子树$T_1$中所有键大于 等于$K_1$小于 $K_2$，以此类推

  • B树是完美平衡的：所有叶子节点在同一层上

查找

算法

  • 输入：B树、目标查找键
  • 输出：查找键所属B树节点（若存在）

  • 从根节点开始，比较查找键k和节点中键序列大小

    • 节点中键有序，若B树阶数足够大，可考虑折半查找

  • 若在节点键序列中找到匹配键，则查找成功、返回

  • 否则根据比较结果选择合适分支，顺着指针链前进，在相应子女 节点中进行查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
BTreeSearch(T, k):
	// 在B树中搜索键
	// 输入：B树根节点T、目标查找键k
	// 输出：目标键所在节点、目标键在节点中序号
	i = 0
	cur = T

	// 遍历寻找目标键对应键、分支
	while i < cur.degree and k > cur.key_slots[i]:
		i += 1

	if i < cur.degree and k == cur.key_slots[i]:
		return cur, i
	elif cur.is_leaf():			// 未找到目标键
		return cur, -1
	else:
		return BTreeSearch(cur.ptr_slots[i], k)

分裂

算法

  • 输入：待分裂节点父节点、待分裂节点序号

  • 计算待分裂节点分裂中心

    • 将分裂中心右侧数据移动至新节点

  • 将节点分裂中心、新节点提升至父节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
BTreeNodeSplit(T, ptr_idx):
	// 分裂B树中节点
	// 输入：待分裂节点父节点`T`、待分裂节点序号`ptr_idx`

	nnode = BTreeNode()
	fnode = T.ptr_slots[ptr_idx]

	// 分裂中心
	mid = fnode.degree // 2

	// 复制右半部分键至新节点
	nnode.key_slots[:fnode.degree - mid] = fnode.key_slots[mid:fnode.degree]
	fnode.key_slots[mid:fnode.degree] = NULL

	// 若原节点非叶子节点，复制右半部分指针至新节点
	if not fnode.is_leaf():
		nnode.ptr_slots[:fnode.degree + 1 - mid] = fnode.ptr_slots[mid: fnode.degree + 1]
		fnode.ptr_slots[mid: fnode.degree+1] = NULL

	// 修改两节点度
	nnode.degree = fnode.degree - mid
	fnode.degree = mid

	// 将分裂中心提升至父节点
	// 修改父节点指向子女节点指针
	T.key_slots.insert(fnode.key_slots[mid], ptr_idx)
	T.ptr_slots.insert(nnode, ptr_idx+1)	// 原节点指针不变

插入

  • 输入：B树根T、待插入键K
  • 假设B树中不存在键K，否则查找、更新对应值即可
  • 根据需要插入键K，查找需要插入的叶子节点L
  • 若叶子节点L键数小于m-1，直接插入结束
  • 否则以叶子节点键值中位数mid为中心分裂
    • 将mid插入叶子节点L父节点P中
    • 将mid左子支指向分裂后左子树、右子支指向分裂后右子树
  • 对父节点尝试操作
1
2
3
4
5
6
7
8
9
10
11
12
13
BTreeInsert(T, k)
	// 向B树中插入不存在键K
	// 输入：B树根T、待插入键k

	// 找到键`k`应该插入的叶子节点`L`
	L, _ = BTreeSearch(T, k)
	L.key_slots.insert_in_order(k)


	// 若节点已满、须分裂
	while L.is_full():
		BTreeNodeSplit(L.parent_ptr, L.get_index())
		L = L.parent_ptr
  • 此实现是考虑节点都有空位容纳新键，节点插入新键后再 判断是否需要分裂

删除#todo

应用

  • 类似一般查找树，把数据记录插入初始为空的树中构造B树

B+树

B+树：B树的一种变形树

  • 其中非叶节点只有索引作用，跟记录相关信息均存放在 叶结点中
  • B+树中所有叶结点构成有序链表，可以按照键次序遍历

查找

算法

  • 从根开始，比较查找键K和节点中键大小，选择合适指针，顺着 指针链前进

  • 指针链指向可能包含查找键的叶子节点，在其中查找K

    • 父母节点、叶子节点都是有序的，如果B树次数足够 大，可以考虑使用折半查找

算法效率

以B树作索引存储大型数据文件为例

  • 查找指定查找键访问B树节点数量为B树高度$h+1$ （即磁盘访问次数）

  • 次数为m、高度为h的B树能够包含最少节点数为 $n \geqslant 4 \lceiling m/2 \rceiling ^ {h-1} -1$， 即$h \leqslant \lfloor log_{[m/2]} \frac {n+1} 4 \rfloor + 1$

  • 所以在B树中查找，访问磁盘次数$\in O(logn)$

    • 实际应用中，磁盘访问次数很少超过3，因为B树的根、甚至 是第一层节点会存储在内存中减少磁盘访问次数

插入

算法

  • 查找新记录键K对应的叶子节点

  • 若叶子节点中还有空间存放此记录，在保持键有序的情况下插入

  • 若节点中没有空间

    • 将节点分裂，后半部分记录放在新节点中
    • 新节点中最小键$K^{‘}$、指向其的指针插入原叶子节点 父母节点中（原叶子节点键、指针之后）
    • 插入过程可以一直回溯到树根，甚至直到树根分裂

其他考虑

  • 查找新记录对应叶子节点时就分裂满节点，可以避免递归分裂
  • 将满叶子节点中部分键移动给兄弟节点，同时替换父母节点中的 键值（保证B树特点），增加少许复杂度以节约空间

算法特点

  • 算法效率
    • 算法时间效率$\in O(logn)$

应用

  • B+树是存储结构化记录数据集合最重要的索引结构
    • 所有数据记录（键）按照升序存储在叶子节点中，其父母 节点作为索引
    • B+树中节点常常对应磁盘中页
    • 考虑到访问磁盘页面是比较内存中键值比较时间多好几个 数量级，磁盘访问次数是衡量B树效率的主要指标

标

查找/搜索树

https://xyy15926.github.io/Algorithm/Data-Structure/tree_search.html

Author

UBeaRLy

Posted on

2019-06-04

Updated on

2019-06-04

Licensed under

#

Like this article? Support the author with

Comments

Categories

Follow

Recents

Advertisement

follow.it

×