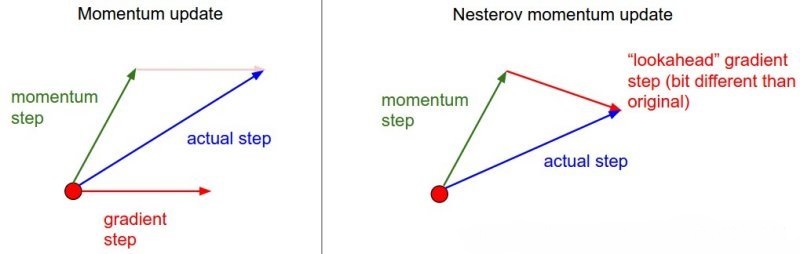
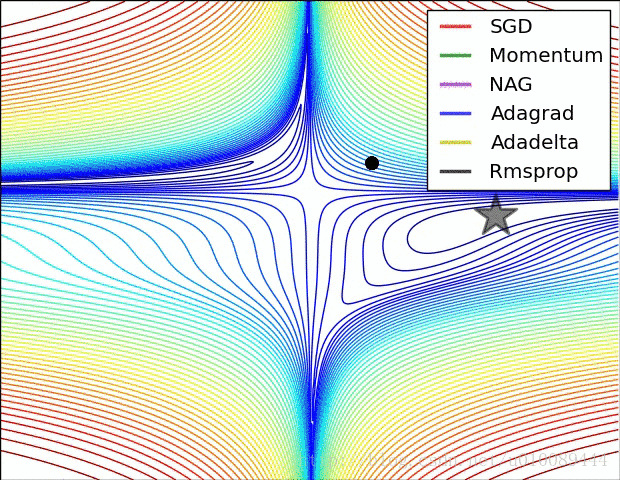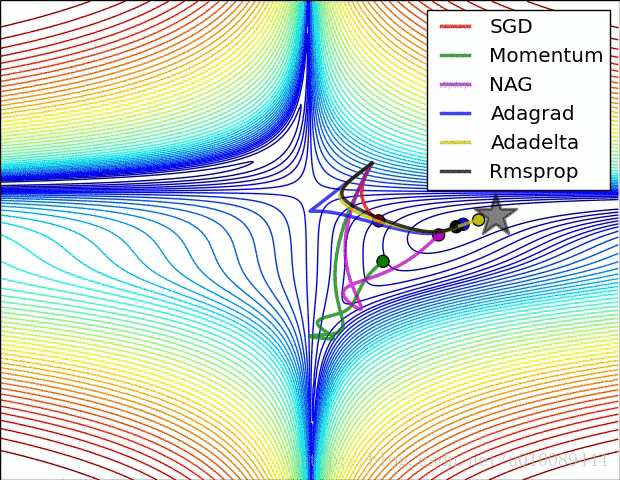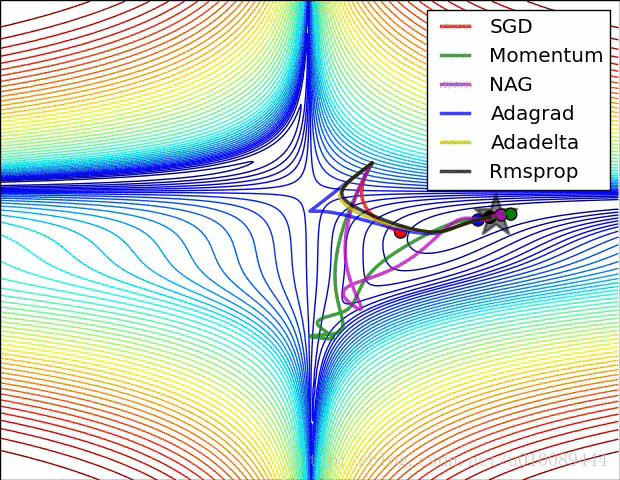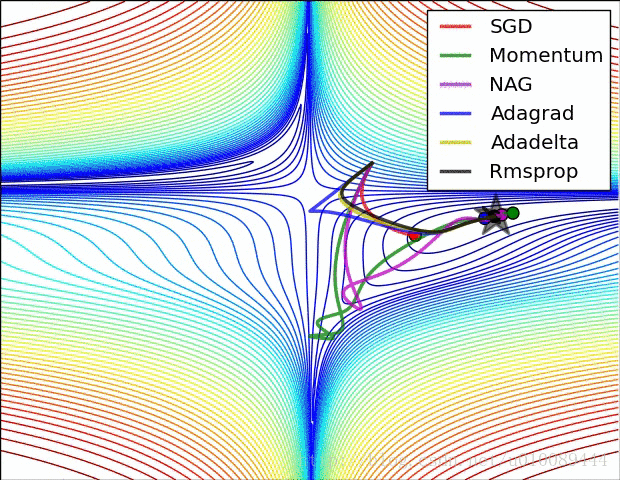
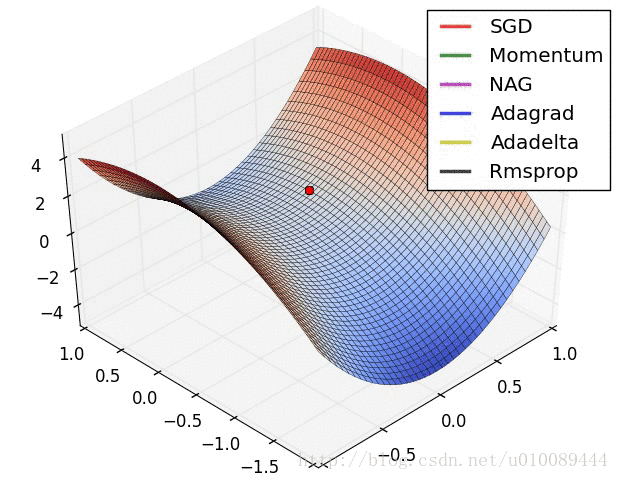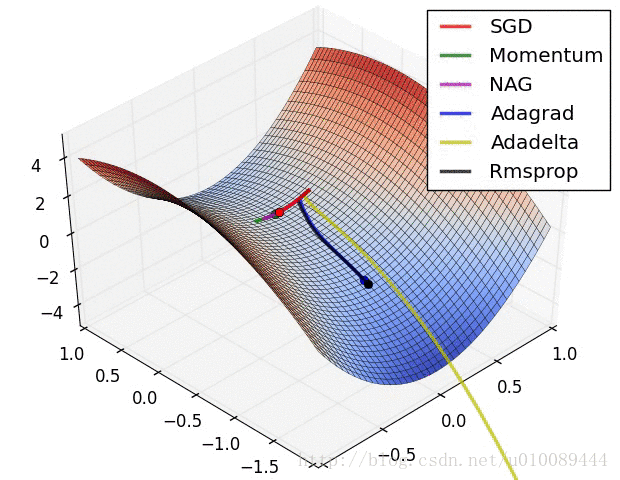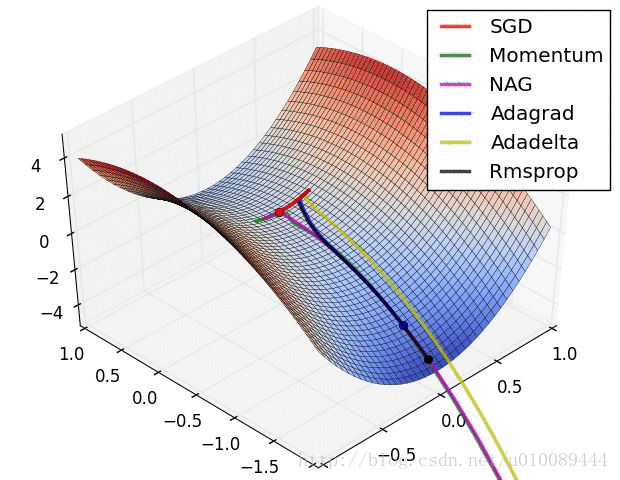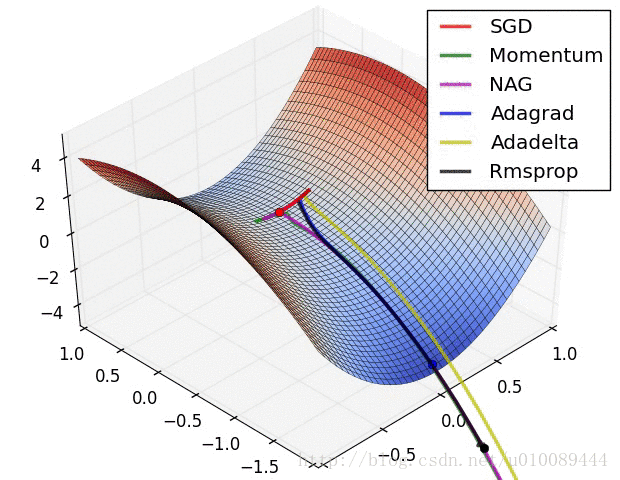
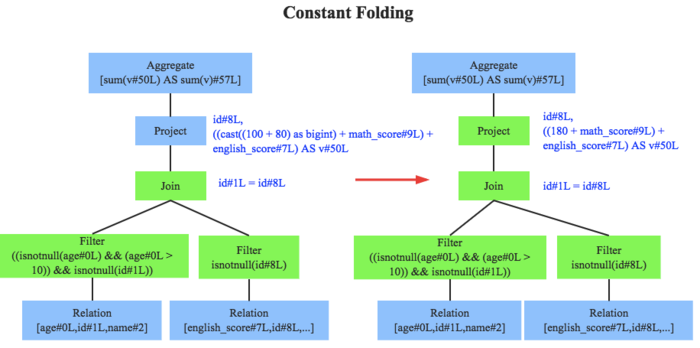
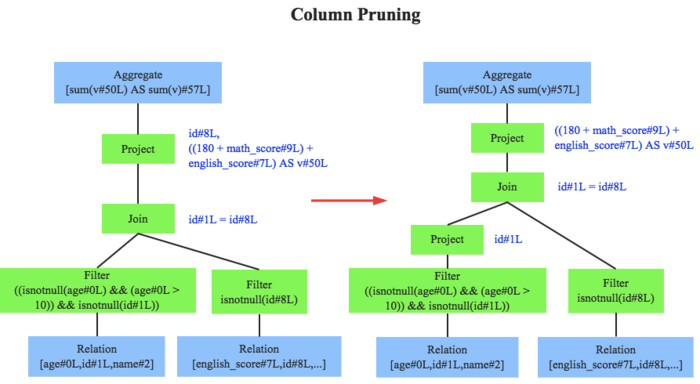
无约束优化特殊问题
正定二次目标函数
非线性最小二乘
- $r_i(x)$:通常为非线性函数
- $r(x) = (r_1(x), \cdots, r_n(x))^T$
- $x \in R^n, m \geq n$
则
- 为$r(x)$的Jacobi矩阵
Gauss-Newton法
Newton法中为简化计算,略去其Hesse矩阵中 $\sum_{i=1}^m r_i(x) \nabla^2 r_i(x)$项,即直接求解 方程组
算法
同Newton法,仅求解Newton方程改为求解以上方程组
特点
实际问题中
- 局部解$x^{ }$对应的目标函数值$f(x^{ })$接近0 时,$|r(x^{(k)})|$较小
- 曲线$r_i(x)$接近直线, $\nabla^2 r_i(x) \approx 0$
采用Gauss-Newton法效果较好,否则效果一般
矩阵$J(x^{(k)})^T J(x^{(k)})$是半正定矩阵,当Jacobi矩阵 列满秩时为正定矩阵,此时虽然$d^{(k)}$是下降方向,但仍需 类似修正牛顿法增加一维搜索策略保证目标函数值不上升
Levenberg-Marquardt方法
但$J(x^{(k)})$中各列线性相关、接近线性相关,则求解 Newton-Gauss方法中的方程组会出现困难,可以改为求解
- $v$:迭代过程中需要调整的参数,LM方法的关键即如何调整
定理1
- 若$d(v)$是以上方程组的解,则$|d(v)|^2$是$v$的连续下降 函数,且$v \rightarrow +\infty, |d(v)| \rightarrow 0$
$J(x^{(k)})^T J(x^{(k)})$是对称半正定矩阵,则存在正交阵
则可以解出$|d(v)|^2$
- 增大$v$可以限制$|d^{(k)}|$,所以LM方法也被称为阻尼最小 二乘法
定理2
- 若$d(v)$是以上方程的解,则$d(v)$是$f(x)$在$x^{(k)}$处的 下降方向,且$v \rightarrow + \infty$时,$d(v)$的方向与 $-J(x^{(k)})^T r(x^{(k)})$方向一致
- 下降方向:$\nabla f(x^{(k)}) d(v) < 0$即可
- 方向一致:夹角余弦
- $v$充分大时,LM方法产生的搜索方向$d^{(k)}$和负梯度方向 一致
参数调整方法
使用梯度、近似Hesse矩阵定义二次函数
其增量为
目标函数增量
定义$\gamma_k = \frac {\Delta f^{(k)}} {\Delta q^{(k)}}$
$\gamma_k$接近1说明$\Delta f^{(k)}$接近$\Delta q^{(k)}$
- 即$f(x^{(k)} + d^{(k+1)})$接近$q(d^{(k)})$
- 即$f(x)$在$x^{(k)}$附近接近二次函数
- 即使用Gauss-Newton方法求解最小二乘问题效果较好
- 即LM方法求解时$v$参数应该较小
$\gamma_k$接近0说明$\Delta f^{(k)}$与$\Delta q^{(k)}$ 近似程度不好
- $d^{(k)}$不应取得过大,应减少$d^{(k)}$得模长
- 应该增加参数$v$进行限制
- 迭代方向趋近于负梯度方向
$\gamma_k$适中时,认为参数$v$选取合适,不做调整
- 临界值通常为0.25、0.75
算法
初始点$x^{(1)}$、初始参数$v$(小值)、精度要求$\epsilon$ ,置k=k+1
若$|J(x^{(k)})^T r(x^{(k)})| < \epsilon$,则停止计算, 得到问题解$x^{(k)}$,否则求解线性方程组
得到$d^{(k)}$
置$x^{(k+1)} = x^{(k)} + d^{(k)}$,计算$\gamma_k$
若
- $\gamma < 0.25$,置$v_{k+1} = 4 v_k$
- $\gamma > 0.75$,置$v_{k+1} = v_k / 2$
- 否则置$v_{k+1} = v_k$
置k=k+1,转2