Posted 2019-07-13Updated 2019-07-13Math Mixin16 minutes read (About 2380 words)

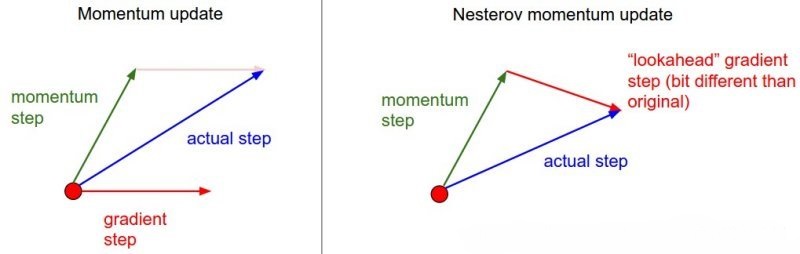
Kernel Function

对输入空间 $X$ （欧式空间 $R^n$ 的子集或离散集合）、特征空间 $H$ ，若存在从映射 $$
  \phi(x): X \rightarrow H
  K(x,z) = \phi(x) \phi(z)
$$ 则称 $K(x,z)$ 为核函数、 $\phi(x)$ 为映射函数，其中 $\phi(x) \phi(z)$ 表示内积

特征空间 $H$ 一般为无穷维
- 特征空间必须为希尔伯特空间（内积完备空间）

映射函数 $\phi$

映射函数 $\phi$：输入空间 $R^n$ 到特征空间的映射 $H$ 的映射
对于给定的核 $K(x,z)$ ，映射函数取法不唯一，映射目标的特征空间可以不同，同一特征空间也可以取不同映射，如：
- 对核函数 $K(x, y) = (x y)^2$ ，输入空间为 $R^2$ ，有
  $\begin{align*} (xy)^2 & = (x_1y_1 + x_2y_2)^2 \\ & = (x_1y_1)^2 + 2x_1y_1x_2y_2 + (x_2y_2)^2 \end{align*}$
- 若特征空间为$R^3$，取映射
  $\phi(x) = (x_1^2, \sqrt 2 x_1x_2, x_2^2)^T$
  或取映射
  $\phi(x) = \frac 1 {\sqrt 2} (x_1^2 - x_2^2, 2x_1x_2, x_1^2 + x_2^2)^T$
- 若特征空间为$R^4$，取映射
  $\phi(x) = (x_1^2, x_1x_2, x_1x_2, x_2^2)^T$

核函数 $K(x,z)$

Kernel Trick 核技巧：利用核函数简化映射函数 $\phi(x)$ 映射、内积的计算技巧
- 避免实际计算映射函数
- 避免高维向量空间向量的存储
核函数即在核技巧中应用的函数
- 实务中往往寻找到的合适的核函数即可，不关心对应的映射函数
- 单个核函数可以对应多个映射、特征空间
核技巧常被用于分类器中
- 根据 Cover’s 定理，核技巧可用于非线性分类问题，如在 SVM 中常用
- 核函数的作用范围：梯度变化较大的区域
  - 梯度变化小的区域，核函数值变化不大，所以没有区分能力

Cover’s 定理可以简单表述为：非线性分类问题映射到高维空间后更有可能线性可分

正定核函数

设 $X \subset R^n$，$K(x,z)$ 是定义在 $X X$的对称函数，若 $\forall x_i \in \mathcal{X}, i=1,2,…,m$，$K(x,z)$ 对应的 Gram* 矩阵 $$
  G = [K(x_i, x_j)]_{m*m}
$$ 是半正定矩阵，则称 $K(x,z)$ 为正定核

可用于指导构造核函数
- 检验具体函数是否为正定核函数不容易
- 正定核具有优秀性质
  - SVM 中正定核能保证优化问题为凸二次规划，即二次规划中矩阵 $G$ 为正定矩阵

欧式空间核函数

Linear Kernel

线性核：最简单的核函数

$k(x, y) = x^T y$

特点
- 适用线性核的核算法通常同普通算法结果相同
  - KPCA 使用线性核等同于普通 PCA

Polynomial Kernel

多项式核：non-stational kernel

$K(x, y) = (\alpha x^T y + c)^p$

特点
- 适合正交归一化后的数据
- 参数较多，稳定
  todo
应用场合
- SVM：p 次多项式分类器
  $f(x) = sgn(\sum_{i=1}^{N_s} \alpha_i^{*} y_i (x_i x + 1)^p + b^{*})$

Gaussian Kernel

高斯核：radial basis kernel，经典的稳健径向基核

$K(x, y) = exp(-\frac {\|x - y\|^2} {2\sigma^2})$

$\sigma$：带通，取值关于核函数效果，影响高斯分布形状

高估：分布过于集中，靠近边缘非常平缓，表现类似像线性一样，非线性能力失效

低估：分布过于平缓，失去正则化能力，决策边界对噪声高度敏感

特点
- 对数据中噪声有较好的抗干扰能力
对应映射：省略分母
$\begin{align*} K(x, y) & = exp(-(x - y)^2) \\ & = exp(-(x^2 - 2 x y - y^2)) \\ & = exp(-x^2) exp(-y^2) exp(2xy) \\ & = exp(-x^2) exp(-y^2) \sum_{i=0}^\infty \frac {(2xy)^i} {i!} \\ & = \phi(x) \phi(y) \\ \phi(x) & = exp(-x^2)\sum_{i=0}^\infty \sqrt {\frac {2^i} {i!}} x^i \end{align*}$
即高斯核能够把数据映射至无穷维
应用场合
- SVM：高斯radial basis function分类器
  $f(x) = sgn(\sum_{i=1}^{N_s} \alpha_i^{*} y_i exp(-\frac {\|x - y\|^2} {2\sigma^2}) + b^{*})$

Exponential Kernel

指数核：高斯核变种，仅去掉范数的平方，也是径向基核

$K(x, y) = exp(-\frac {\|x - y\|} {2\sigma^2})$

降低了对参数的依赖性
适用范围相对狭窄

Laplacian Kernel

拉普拉斯核：完全等同于的指数核，只是对参数$\sigma$改变敏感性稍低，也是径向基核

$K(x, y) = exp(-\frac {\|x - y\|} {\sigma^2})$

ANOVA Kernel

方差核：径向基核

$k(x,y) = \sum_{k=1}^n exp(-\sigma(x^k - y^k)^2)^d$

在多维回归问题中效果很好

Hyperbolic Tangent/Sigmoid/Multilayer Perceptron Kernel

Sigmoid核：来自神经网络领域，被用作人工神经元的激活函数

$k(x, y) = tanh(\alpha x^T y + c)$

条件正定，但是实际应用中效果不错
参数
- $\alpha$：通常设置为$1/N$，N是数据维度

使用Sigmoid核的SVM等同于两层感知机神经网络

Ration Quadratic Kernel

二次有理核：替代高斯核，计算耗时较小

$k(x, y) = 1 - \frac {\|x - y\|^2} {\|x - y\|^2 + c}$

Multiquadric Kernel

多元二次核：适用范围同二次有理核，是非正定核

$k(x, y) = \sqrt {\|x - y\|^2 + c^2}$

Inverse Multiquadric Kernel

逆多元二次核：和高斯核一样，产生满秩核矩阵，产生无穷维的特征空间

$k(x, y) = \frac 1 {\sqrt {\|x - y\|^2 + c^2}}$

Circular Kernel

环形核：从统计角度考虑的核，各向同性稳定核，在$R^2$上正定

$k(x, y) = \frac 2 \pi arccos(-\frac {\|x - y\|} \sigma) - \frac 2 \pi \frac {\|x - y\|} \sigma \sqrt{1- \frac {\|x - y\|^2} \sigma}$

Spherical Kernel

类似环形核，在$R^3$上正定

$k(x, y) = 1 - \frac 3 2 \frac {\|x - y\|} \sigma + \frac 1 2 (\frac {\|x - y\|} \sigma)^3$

Wave Kernel

波动核

$k(x, y) = \frac \theta {\|x - y\|} sin(\frac {\|x - y\|} \theta)$

适用于语音处理场景

Triangular/Power Kernel

三角核/幂核：量纲不变核，条件正定

$k(x, y) = - \|x - y\|^d$

Log Kernel

对数核：在图像分隔上经常被使用，条件正定

$k(x, y) = -log(1 + \|x - y\|^d)$

Spline Kernel

样条核：以分段三次多项式形式给出

$k(x, y) = 1 + x^t y + x^t y min(x, y) - \frac {x + y} 2 min(x, y)^2 + \frac 1 3 min(x, y)^2$

B-Spline Kernel

B-样条核：径向基核，通过递归形式给出

$\begin{align*} k(x, y) & = \prod_{p=1}^d B_{2n+1}(x_p - y_p) \\ B_n(x) & = B_{n-1} \otimes B_0 \\ & = \frac 1 {n!} \sum_{k=0}^{n+1} \binom {n+1} {r} (-1)^k (x + \frac {n+1} 2 - k)_{+}^n \end{align*}$

$x_{+}^d$：截断幂函数 $x_{+}^d = \left \{ \begin{array}{l} x^d, & if x > 0 \\ 0, & otherwise \\ \end{array} \right.$

Bessel Kernel

Bessel核：在theory of function spaces of fractional smoothness 中非常有名

$k(x, y) = \frac {J_{v+1}(\sigma\|x - y\|)} {\|x - y\|^{-n(v + 1)}}$

$J$：第一类Bessel函数

Cauchy Kernel

柯西核：源自柯西分布，是长尾核，定义域广泛，可以用于原始维度很高的数据

$k(x, y) = \frac 1 {1 + \frac {\|x - y\|^2} {\sigma}}$

Chi-Square Kernel

卡方核：源自卡方分布

$\begin{align*} k(x, y) & = 1 - \sum_{i=1}^d \frac {(x_i - y_i)^2} {\frac 1 2 (x_i + y_i)} \\ & \frac {x^t y} {\|x + y\|} \end{align*}$

Histogram Intersection/Min Kernel

直方图交叉核：在图像分类中经常用到，适用于图像的直方图特征

$k(x, y) = \sum_{i=1}^d min(x_i, y_i)$

Generalized Histogram Intersection

广义直方图交叉核：直方图交叉核的扩展，可以应用于更多领域

$k(x, y) = \sum_{i=1}^m min(|x_i|^\alpha, |y_i|^\beta)$

Bayesian Kernel

贝叶斯核：取决于建模的问题

$\begin{align*} k(x, y) & = \prod_{i=1}^d k_i (x_i, y_i) \\ k_i(a, b) & = \sum_{c \in \{0, 1\}} P(Y=c | X_i = a) P(Y=c | x_k = b) \end{align*}$

Wavelet Kernel

波核：源自波理论

$k(x, y) = \prod_{i=1}^d h(\frac {x_i - c} a) h(\frac {y_i - c} a)$

参数
- $c$：波的膨胀速率
- $a$：波的转化速率
- $h$：母波函数，可能的一个函数为 $h(x) = cos(1.75 x) exp(-\frac {x^2} 2)$
转化不变版本如下
$k(x, y) = \prod_{i=1}^d h(\frac {x_i - y_i} a)$

离散数据核函数

String Kernel

字符串核函数：定义在字符串集合（离散数据集合）上的核函数

$\begin{align*} k_n(s, t) & = \sum_{u \in \sum^n} [\phi_n(s)]_u [\phi_n(t)]_u \\ & = \sum_{u \in \sum^n} \sum_{(i,j): s(i) = t(j) = u} \lambda^{l(i)} \lambda^{l(j)} \end{align*}$

$[\phin(s)]_n = \sum{i:s(i)=u} \lambda^{l(i)}$：长度大于等于n的字符串集合$S$到特征空间 $\mathcal{H} = R^{\sum^n}$的映射，目标特征空间每维对应一个字符串$u \in \sum^n$

$\sum$：有限字符表

$\sum^n$：$\sum$中元素构成，长度为n的字符串集合

$u = s(i) = s(i1)s(i_2)\cdots s(i{|u|})$：字符串s的子串u（其自身也可以用此方式表示）

$i =(i1, i_2, \cdots, i{|u|}), 1 \leq i1 < i_2 < … < i{|u|} \leq |s|$：序列指标

$l(i) = i_{|u|} - i_1 + 1 \geq |u|$：字符串长度，仅在序列指标$i$连续时取等号（$j$同）

$0 < \lambda \leq 1$：衰减参数

两个字符串s、t上的字符串核函数，是基于映射$\phi_n$的特征空间中的内积
- 给出了字符串中长度为n的所有子串组成的特征向量的余弦相似度
- 直观上，两字符串相同子串越多，其越相似，核函数值越大
- 核函数值可由动态规划快速计算（只需要计算两字符串公共子序列即可）
应用场合
- 文本分类
- 信息检索
- 信物信息学

Posted 2019-07-13Updated 2019-07-13Math Mixina few seconds read (About 30 words)

函数说明

约定

I：示性/指示函数
- 满足条件时取1，否则取0
sign：符号函数
- >0：取1
- <0：取-1

Posted 2019-06-27Updated 2019-06-27Math Analysis / Optimization7 minutes read (About 999 words)

Lagrange 对偶

Langrangian Duality

拉格朗日对偶

考虑优化问题：找到$f(x)$满足约束的最好下界
$z^{*} = \min_{x} f(x) \\ \begin{align*} s.t. \quad & g_i(x) \leq 0, i=1,2,\cdots,m \\ & x \in X \end{align*}$
考虑方程组
- 方程组无解：$v$是优化问题的一个下界
- 方程组有解：则可以推出
  - 显然，取$g_1 + g_2 = 0, g_1(x) > 0$是反例，不能推出原方程有解
- 由以上方程组有解逆否命题：方程组无解充分条件如下
  $\exists \lambda \geq 0, \min_{x} f(x) + \sum _{i=1}^m \lambda_ig_i(x) \geq v$
由此方法推出的最好下界，即拉格朗日对偶问题
$v^{*} = \max_{\lambda \geq 0} \min_{x} f(x) + \sum_{i=1}^m \lambda_ig_i(x)$

说明

拉格朗日对偶对实数域上的优化问题都存在，对目标函数、约束函数都没有要求
强对偶定理：$v^{} = z^{}$，需要$f,g$满足特定条件才成立
- 线性规划
- 半正定规划
- 凸优化
- 即需要给约束条件加以限制，使得 $\forall \lambda \geq 0, \exists x, f(x) + \sum_{i=1}^m \lambda_ig_i(x) < v$ 是上述方程组有解的冲要条件
弱对偶定理：$v^{} \leq z^{}$，永远成立（以上即可证）
- 通过弱对偶定理，可以得到原问题的一个下界
- 对求解原问题有帮助，比如：分支界限法中快速求下界
对偶问题相关算法往往原问题算法在实际应用中往往更加有效
- dual-simplex
- primal-dual interior point method
- augmented Lagrangian Method

原始问题

约束最优化问题

$\begin{array}{l} \min_{x \in R^n} & f(x) \\ s.t. & c_i(x) \leq 0, i = 1,2,\cdots,k \\ & h_j(x) = 0, j = 1,2,\cdots,l \end{array}$

Generalized Lagrange Function

引入Generalized Lagrange Function
- $x=(x_1, x_2, \cdots, x_n) \in R^n$
- $\alpha_i \geq 0, \beta_j$：拉格朗日乘子
考虑关于x的函数
- $P$：primal，原始问题
- 若x满足原始问题的两组约束条件，则$\theta_P(x)=f(x)$
- 若x违反等式约束j，取$\beta_j \rightarrow \infty$，则有$\theta_P(x) \rightarrow \infty$
- 若x违反不等式约束i，取$\alpha_i \rightarrow \infty$ ，则有$\theta_P(x) \rightarrow \infty$
则有
则极小化问题，称为广义拉格朗日函数的极小极大问题
$\min_x \theta_P(x) = \max_{\alpha, \beta: \alpha_i \geq 0} L(x, \alpha, \beta)$
与原始最优化问题等价，两问题最优值相同，记为
$p^{*} = \min_x \theta_P(x)$

对偶问题

定义
$\theta_D (\alpha, \beta) = \min_x L(x, \alpha, \beta)$
再考虑极大化$\theta_D(\alpha, \beta)$，得到广义拉格朗日函数的极大极小问题，即
$\max_{\alpha, \beta: \alpha \geq 0} \theta_D(\alpha, \beta) = \max_{\alpha, \beta: \alpha \geq 0} \min_x L(x, \alpha, \beta)$
表示为约束最优化问题如下
$\begin{align*} \max_{\alpha, \beta} & \theta_D(\alpha, \beta) = \max_{\alpha, \beta} \min_x L(x, \alpha, \beta) \\ s.t. & \alpha_i \geq 0, i=1,2,\cdots,k \end{align*}$
称为原始问题的对偶问题，其最优值定义记为
$d^{*} = \max_{\alpha, \beta: \alpha \geq 0} \theta_D(\alpha, \beta)$

原始、对偶问题关系

定理1

若原始问题、对偶问题都有最优值，则 $d^{*} = \max_{\alpha, \beta: \alpha \geq 0} \min_x L(x, \alpha, \beta) \leq \min_x \max_{\alpha, \beta: \alpha \geq 0} L(x, \alpha, \beta) = p^{*}$

$\forall x, \alpha, \beta$有
$\theta_D(\alpha, \beta) = \min_x L(x, \alpha, \beta) \leq L(x, \alpha, \beta) \leq \max_{\alpha, \beta: \alpha \geq 0} = \theta_P(x)$
即
$\theta_D(\alpha, \beta) \leq \theta_P(x)$
而原始、对偶问题均有最优值，所以得证

设$x^{}$、$\alpha^{}, \beta^{}$分别是原始问题、对偶问题的可行解，且$d^{} = p^{*}$，则其分别是原始问题、对偶问题的最优解

Posted 2019-06-09Updated 2021-08-02Python / Py3stda few seconds read (About 7 words)

数字、数学

`numbers`

`math`

`cmath`

`decimal`

`fractions`

`random`

`statics`

Posted 2019-06-04Updated 2021-08-04Math Analysis / Optimization16 minutes read (About 2327 words)

Gradient Descent Method

思想：最速下降&牛顿

对目标函数$f(x)$在$x^{(1)}$进行展开

$f(x) = f(x^{(1)}) + \nabla f(x^{(1)})(x - x^{(1)})+ \frac 1 2 \nabla^2 f(x^{(1)})(x - x^{(1)})^2 + o((x - x^{(1)})^2)$

最速下降法：只保留一阶项，即使用线性函数近似原目标函数

Newton法：保留一阶、二阶项，即使用二次函数近似

利用近似函数求解元素问题极小值
- 最速下降法：线性函数无极值，需要确定步长、迭代
- Newton法：二次函数有极值，直接求导算出极值、迭代
最速下降法
- 只考虑一阶导：甚至说根本没有考虑拟合原目标函数
Newton法
- 考虑二阶导：每步迭代还考虑了二阶导，即当前更新完毕后，下一步能够更好的更新（二阶导的意义）
- 甚至从后面部分可以看出，Newton法甚至考虑是全局特征，不只是局部性质（前提目标函数性质足够好）
- 二次函数拟合更接近函数极值处的特征

最速下降算法

思想

设$x=x(t)$为最优点$x$从初始点、沿负梯度方向经过的曲线，则有
- $t_1, x^{(1)}$：初始时刻、初始位置
可以证明，$x(t)$解存在，且$t \rightarrow \infty$时，有 $x(t) \rightarrow x^{ * }$，即得到无约束问题最优解
但微分方程组求解可能很麻烦，可能根本无法求解
- 考虑将以上曲线离散化，每次前进到“不应该”前进为止
- 然后更换方向，逐步迭代得到最优解

算法

搜索方向最速下降方向：负梯度方向

终止准则：$\nabla f(x^{(k)})=0$

取初始点$x^{(1)}$，置k=1
若$\nabla f(x^{(k)})=0$，则停止计算，得到最优解，否则置
$d^{(k)} = -\nabla f(x^{(k)})$
以负梯度作为前进方向
一维搜索，求解一维问题
$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$
得$\alpha_k$前进步长，置
$x^{(k+1)} = x^{(k)} + \alpha_k d^{(k)}$
置k=k+1，转2

最速下降算法不具有二次终止性

叠加惯性

模拟物体运动时惯性：指数平滑更新步长

momentum

Momentum

冲量方法：在原始更新步上叠加上次更新步，类似指数平滑

$v^{(t)} = \gamma v^{(t-1)} + (1 - \gamma) \eta \bigtriangledown_\theta L(\theta^{(t-1)}) \\ \theta^{(t)} = \theta^{(t-1)} - v^{(t)}$

$v^{(t)}$：第$t$步时第k个参数更新步

$L(\theta)$：往往是batch损失函数

更新参数时，一定程度保持上次更新方向
可以在一定程度上保持稳定性，学习速度更快
能够越过部分局部最优解

Nesterov Momentum

NGA：在使用冲量修正最终方向基础上，使用冲量对当前 参数位置进行修正，即使用“未来”位置计算梯度

先使用冲量更新一步
再在更新后位置计算新梯度进行第二步更新

$v^{(t)} = \gamma v^{(t-1)} + \eta \bigtriangledown_\theta L(\theta^{(t-1)} - \gamma v^{(t-1)}) \\ \theta^{(t)} = \theta^{(t-1)} - v^{(t)}$

动态学习率

学习率太小收敛速率缓慢、过大则会造成较大波动
在训练过程中动态调整学习率大小较好

模拟退火思想：达到一定迭代次数、损失函数小于阈值时，减小学习速率

param_estimation_comparion_1 param_estimation_comparion_2

Vanilla Gradient Descent

每次迭代减小学习率$\eta$

$\eta^{(t)} = \frac \eta {\sqrt {t+1}} \\ \theta^{(t)} = \theta^{(t-1)} - \eta^{(t)} \bigtriangledown_\theta L(\theta^{(t-1)})$

学习率逐渐减小，避免学习后期参数在最优解附近反复震荡

Adagrad

adaptive gradient：训练中不同参数学习率随着迭代次数、梯度动态变化，使得参数收敛更加平稳

$v^{(t)}_k = \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ \theta^{(t)}_k = \theta^{(t-1)}_k - \frac \eta {\sqrt {\sum_{i=0}^{t-1} (v^{(i)}_k)^2 + \epsilon}} v^{(t)}_k$

$\epsilon$：fuss factor，避免分母为0

$\theta^{(t)}_k$：第t轮迭代完成后待估参数第k个分量（之前未涉及参数间不同，统一为向量）

特点
- 较大梯度参数真正学习率会被拉小；较小梯度真正学习率参数被拉小幅度较小
- 可以和异步更新参数结合使用，给不常更新参数更大学习率
缺点
- 在训练后期，分母中梯度平方累加很大，学习步长趋于0，收敛速度慢（可能触发阈值，提前结束训练）

RMSprop

root mean square prop：指数平滑更新学习率分母

$v^{(t)}_k = \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ \theta^{(t)}_k = \theta^{(t-1)}_k - \frac \eta {\sqrt { \gamma \sum_{i=1}^{t-1}(v^{(i)}_k)^2 + (1 - \gamma)((v^{(t)})^2 + \epsilon} } v^{(t)}$

赋予当前梯度更大权重，减小学习率分母，避免学习速率下降太快

Adam

adptive moment estimation：指数平滑更新步、学习率分母

$\begin{align*} v^{(t)}_k & = \gamma_1 v^{(t-1)}_k + (1 - \gamma_1) \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ s^{(t)}_k & = \gamma_2 s^{(t-1)}_k + (1 - \gamma_2) \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \hat{v^{(t)}_k} & = \frac {v^{(t)}_k} {1 - \gamma_1^t} \\ \hat{s^{(t)}_k} & = \frac {s^{(t)}_k} {1 - \gamma_2^t} \\ \theta^{(t)}_k & = \theta^{(t-1)}_k - \frac \eta {\sqrt{\hat{s^{(t)}_k} + \epsilon}} \hat{v^{(t)}_k} \end{align*}$

$\gamma_1$：通常为0.9

$\gamma_2$：通常为0.99

$\hat{v^{(t)}_k} = \frac {v^{(t)}_k} {1 - \gamma_1^t}$ ：权值修正，使得过去个时间步，小批量随机梯度权值之和为1

利用梯度的一阶矩$v^{(t)}$、二阶矩$s^{(t)}$动态调整每个参数学习率
类似于mommentum、RMSprop结合
经过偏执矫正后，每次迭代学习率都有确定范围，参数比较平稳

Adadelta

指数平滑更新学习率（分子）、学习率分母

$\begin{align*} s^{(t)}_k & = \gamma_1 s^{(t-1)}_k + (1 - \gamma_1) \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \hat{v^{(t)}_k} & = \sqrt {\frac {\Delta \theta^{(t-1)}_k + \epsilon} {s^{(t)}_k + \epsilon}} \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \Delta \theta^{(t)}_k & = \gamma_1 \Delta \theta^{(t-1)}_k + (1 - \gamma_1) \hat{v^{(t)}_k}^2 \\ \theta^{(t)}_k & = \theta^{(t)}_k - \hat{v^{(t)}_k} \end{align*}$

$s, \Delta \theta$共用超参$\gamma_1$

在RMSprop基础上，使用$\sqrt {\Delta \theta}$作为学习率
$\hat v$：中超参$\gamma_1$在分子、分母“抵消”，模型对超参不敏感

样本量

Singular Loss/Stocastic Gradient Descent

SGD：用模型在某个样本点上的损失极小化目标函数、计算梯度、更新参数

单点损失度量模型“一次”预测的好坏
- 代表模型在单点上的优劣，无法代表模型在总体上性质
- 具有很强随机性
单点损失不常用，SGD范围也不局限于单点损失

损失函数具体参见ml_xxxxx

全局估计

全局损失：用模型在全体样本点上损失极小化目标函数、计算梯度、更新参数

$\theta^{(t)} = \theta^{(t-1)} - \eta \bigtriangledown_\theta L_{total}(\theta_{(t-1)})$

$\theta^{(t)}$：第t步迭代完成后待估参数

$\eta$：学习率

$L{total}(\theta) = \sum{i=1}^N L(\theta, x_i, y_i)$：训练样本整体损失

$N$：训练样本数量

若损失函数有解析解、样本量不大，可一步更新（计算） 完成（传统参数估计场合）
- 矩估计
- 最小二乘估计
- 极大似然估计
否则需要迭代更新参数
- 样本量较大场合
- 并行计算

Mini-Batch Loss

mini-batch loss：用模型在某个batch上的损失极小化目标函数、计算梯度、更新参数

$\theta^{(t)} = \theta^{(t-1)} - \eta \bigtriangledown_\theta L_{batch}(\theta^{(t-1)})$

$L{batch}(\theta)=\sum{i \in B} L(\theta, x_i, y_i)$：当前batch整体损失

$B$：当前更新步中，样本组成的集合batch

batch-loss是模型在batch上的特征，对整体的代表性取决于 batch大小
- batch越大对整体代表性越好，越稳定；越小对整体代表越差、不稳定、波动较大、难收敛
- batch大小为1时，就是SGD
- batch大小为整个训练集时，就是经验（结构）风险
batch-loss是学习算法中最常用的loss，SGD优化常指此
- 实际中往往是使用batch-loss替代整体损失，表示经验风险极小化
- batch-loss同样可以带正则化项，表示结构风险极小化
- 损失极值：SVM（几何间隔最小）

优点

适合样本量较大、无法使用样本整体估计使用
一定程度能避免局部最优（随机batch可能越过局部极值）
开始阶段收敛速度快

缺点

限于每次只使用单batch中样本更新参数，batch-size较小时，结果可能不稳定，往往很难得到最优解
无法保证良好的收敛性，学习率小收敛速度慢，学习率过大则损失函数可能在极小点反复震荡
对所有参数更新应用相同学习率，没有对低频特征有优化（更的学习率）
依然容易陷入局部最优点

Posted 2019-06-04Updated 2019-06-04Math Analysis / Optimization5 minutes read (About 752 words)

Newton's Method

Newton法

思想

若$x^{ * }$是无约束问题局部解，则有
$\nabla f(x^{ * }) = 0$
可求解此问题，得到无约束问题最优解
原始问题是非线性，考虑求解其线性逼近，在初始点$x^{(1)}$ 处泰勒展开
$\nabla f(x) \approx \nabla f(x^{(1)}) + \nabla^2 f(x^{(1)})(x - x^{(1)})$
解得
$x^{(2)} = x^{(1)} - (\nabla^2 f(x^{(1)}))^{-1} \nabla f(x^{(1)})$
作为$x^{ * }$的第二次近似
不断迭代，得到如下序列
- $d^{(k)}$：Newton方向，即以下方程解 $\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$

算法

初始点 $x^{(1)}$、精度要求 $\epsilon$，置 $k=1$
考虑 $|\nabla f(x^{(k)})| \leq \epsilon$
- 若满足，则停止计算，得到最优解 $x^{(k)}$
- 否则求解如下方程，得到 $d^{(k)}$
  $\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$
如下设置，并转2
$x^{(k+1)} = x^{(k)} + d^{(k)}, k = k+1$

特点

优点
- 产生点列 ${x^{k}}$ 若收敛，则具有二阶收敛速率
- 具有二次终止性，事实上对正定二次函数，一步即可收敛
缺点
- 可能会在某步迭代时目标函数值上升
- 当初始点 $x^{(1)}$ 距离最优解 $x^{ * }$ 时，产生的点列可能不收敛，或者收敛到鞍点
- 需要计算 Hesse 矩阵
  - 计算量大
  - Hesse 矩阵可能不可逆，算法终止
  - Hesse 矩阵不正定，Newton 方向可能不是下降方向

阻尼/修正 Newton 法

克服 Newton 法目标函数值上升的缺点
一定程度上克服点列可能不收敛缺点

算法

初始点 $x^{(1)}$、精度要求 $\epsilon$，置 $k=1$
考虑 $|\nabla f(x^{(k)})| \leq \epsilon$
- 若满足，停止计算，得到最优解 $x^{(k)}$
- 否则求解如下方程得到 $d^{(k)}$ $\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$
一维搜索，求解一维问题
$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$
得到 $\alpha_k$，如下设置并转2
$x^{(k+1)} = x^{(k)} + \alpha_k d^{(k)}, k = k+1$

其他改进

Newton 法、修正 Newton 法的改进方向
- 结合最速下降方向修正迭代方向
- Hesse 矩阵不正定情形下的替代

结合最速下降方向

将 Newton 方向和最速下降方向结合

设 $\theta_k$ 是 $$ 之间夹角，显然希望 $\theta < \frac \pi 2$
则置限制条件 $\eta$，取迭代方向
$d^{(k)} = \left \{ \begin{array}{l} d^{(k)}, & cos\theta_k \geq \eta \\ -\nabla f(x^{(k)}), & 其他 \end{array} \right.$

Negative Curvature

当 Hesse 矩阵非正定时，选择负曲率下降方向 $d^{(k)}$（一定存在）

Hesse 矩阵非正定时，一定存在负特征值、相应特征向量 $u$
- 取负曲率下降方向作为迭代方向
  $d^{(k)} = -sign(u^T \nabla f(x^{(k)})) u$
- $x^{(k)}$ 处负曲率方向 $d^{(k)}$ 满足
  ${d^{(k)}}^T \nabla^2 f(x^{(k)}) d^{(k)} < 0$

修正 Hesse 矩阵

取迭代方向 $d^{(k)}$ 为以下方程的解
$(\nabla^2 f(x^{(k)}) + v_k I) d = -\nabla f(x^{k})$

$v_k$：大于 $\nabla^2 f(x^{(k)})$ 最大负特征值绝对值

Posted 2019-05-01Updated 2021-08-04Probability4 minutes read (About 560 words)

常见分布

离散

连续

P-stable Distributions

p_stable distribution：随机变量 $\sum_i v_i X_i$ 、随机变量 $(\sum_i |v_i|^p)^{1/p} X$ 具有相同的分布

$v_1, v_2, \cdots, v_n$：任意实数

$X_1, X_2, \cdots, X_n$：独立同分布$D$随机变量

$X$：服从分布$D$随机变量

$\forall p \in (0, 2]$，稳定分布存在，但仅$p=1,2$时，有解析解
- $p=1$：柯西分布
  $c(x) = \frac 1 \pi \frac 1 {1+x^2}$
- $p=2$：高斯分布
  $g(x) = \frac 1 {\sqrt {2\pi}} e^{-\frac {x^2} 2}$
可以从$[0,1]$上均匀分布获得稳定分布
- 但是概率分布、密度函数没有解析解

性质、用途

若向量 $a$ 中每个元素独立从 p-stable 分布中抽取，则 $|v|_p X = (\sum_i |v_i|^p)^{1/p} X$ 和 $
$ 同分布
- 可用较好计算的内积估计 $|v|_p$
- 考虑到 $a(v_1 - v_2) = av_1 - av_2$，将内积和点之间 $L_p$ 范数距离 $|v_1 - v_2|_p$ 相联系

Exponential Family of Distributions

单变量指数分布概率密度/分布

$\begin{align*} f_X(x|\theta) &= h(x) e^{\eta(\theta) T(x) - A(\theta)} \\ &= h(x) g(\theta) e^{\eta(\theta) T(x)} \\ &= e^{\eta(\theta) T(x) - A(\theta) + B(x)} \end{align*}$

$\eta(\theta)$：nutural parameter，自然参数

$h(x)$：underlying measure，底层观测值

$T(x)$：sufficient statistic，随机变量X的充分统计量

$A(\theta)$：log normalizer，对数规范化

$\eta(\theta), T(x)$：可以是向量，其内积仍为实数
$\eta(\theta) = \theta$时，称分布族为canonical形式
- 总是能够定义$\eta = \eta(\theta)$转为此形式
对数规范化$A(\theta)$使得概率密度函数满足积分为1
$\begin{align*} f(x|\theta) e^{A(\theta)} & = h(x) e^{\eta(\theta)T(x)} \\ \int e^{A(\theta)} f(x|\theta) dx & = \int h(x) e^{\eta(\theta) T(x)} dx \\ e^{A(\theta)} \int f(x|\theta) dx & = \int h(x) e^{\eta(\theta) T(x)} dx \\ A(\theta) & = ln \int h(x) e^{\eta(\theta) T(x)} dx \end{align*}$

https://zhuanlan.zhihu.com/p/148776108

性质

充分统计量$T(x)$可以使用固定几个值，从大量的独立同分布数据中获取信息
todo

Bernoulli分布

$h(x) = 1$
$T(x) = x$
$\eta = log \frac \theta {1 - \theta}$
$A(\theta) = ln(1+e^{\theta})$

Possion

$\theta = \lambda$
$h(x) = \frac 1 {x!}$
$\eta(\theta) = ln\lambda$
$T(x) = x$
$A(\theta) = \lambda$

Normal

$h(x) = \frac 1 {\sqrt{2\pi\sigma^2}} e^{-\frac {x^2} {2\sigma^2}}$
$T(x) = \frac x \sigma$
$A(\theta) = \frac {\mu^2} {2\sigma^2}$
$\eta(\theta) = \frac \mu \sigma$

Posted 2019-04-23Updated 2019-04-23Math Analysis / Optimization12 minutes read (About 1864 words)

Quasi-Newton Method/Variable Metric Method

综述

拟Newton法/变度量法：不需要求解Hesse矩阵，使用一阶导构造二阶信息的近似矩阵

使用迭代过程中信息，创建近似矩阵$B^{(k)}$代替Hesse矩阵
用以下方程组替代Newton方程，其解$d^{(k)}$作为搜索方向
$B^{(k)} d = - \triangledown f(x^{(k)})$

思想

考虑$\triangledown f(x)$在$x^{(k+1)}$处泰勒展开
$\triangledown f(x) \approx \triangledown f(x^{(k+1)}) + \triangledown^2 f(x^{(k+1)})(x - x^{(k+1)})$
取$x = x^{(k)}$，有
- $s^{(k)} = x^{(k+1)} - x^{(k)}$
- $y^{(k)} = \triangledown f(x^{(k+1)}) - \triangledown f(x^{(k)})$
要求$B^{(k)}$近似$\triangledown^2 f(x^{(k)})$，带入并将 $\approx$改为$=$，得到拟Newton方程
$B^{(k+1)} s^{(k)} = y^{(k)}$
并假设$B^{(k)}$对称
拟Newton方程不能唯一确定$B^{(k+1)}$，需要附加条件，自然的想法就是$B^{(k+1)}$可由$B^{(k)}$修正得到，即
$B^{(k+1)} = B^{(k)} + \Delta B^{(k)}$
且修正项$\Delta B^{(k)}$具有“简单形式”

Hesse矩阵修正

对称秩1修正

认为简单指矩阵秩小：即认为$\Delta B^{(k)}$秩为最小值1

设$\Delta B^{(k)} = u v^T$，带入有
- 这里有的书会设$\Delta B^{(k)} = \alpha u v^T$，其实对向量没有必要
- $v^T s^{(k)}$是数，所以$u$必然与共线，同理也没有必要考虑系数，直接取相等即可
- 而且系数不会影响最终结果
可取$u = y^{(k)} - B^{(k)} s{(k)}$，取$v$满足 $v^T s^{(k)} = 1$
由$B^{(k)}$的对称性、并希望$B^{(k+1)}$保持对称，需要 $u, v$共线，则有
$\begin{align*} v & = \lambda u = \lambda (y^{(k)} - B^{(k)} s^{(k)}) \\ 1 & = \lambda (y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)} \end{align*}$
得到$B^{(k)}$的对称秩1修正公式
$B^{(k+1)} = B^{(k)} + \frac {(y^{(k) - B^{(k)} s^{(k)}}) (y^{(k)} - B^{(k)} s^{(k)})^T} {(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)}}$

算法

初始点$x^{(1)}$、初始矩阵$B^{(1)} = I$、精度要求 $\epsilon$、置$k=1$
若$|\triangledown f(x^{(k)})| \leq \epsilon$，停止计算，得到解$x^{(k)}$，否则求解以下方程得到$d^{(k)}$
$B^{(k)} d = -\triangle f(x^{(k)})$
一维搜索，求解
$\arg\min_{\alpha} \phi(\alpha)=f(x^{(k)} + \alpha d^{(k)})$
得到$\alpha_k$，置$x^{(k+1)}=x^{(k)} + \alpha_k d^{(k)}$
修正$B^{(k)}$
$\begin{align*} s^{(k)} & = x^{(k+1)} - x^{(k)} \\ y^{(k)} & = \triangledown f(x^{(k+1)}) - \triangledown f(x^{(k)}) \\ B^{(k+1)} & = B^{(k)} + \frac {(y^{(k) - B^{(k)} s^{(k)}}) (y^{(k)} - B^{(k)} s^{(k)})^T} {(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)}} \end{align*}$
置$k = k+1$，转2

特点

缺点
- 要求$(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)} \neq 0$，否则无法继续计算
- 不能保证正定性传递，只有 $(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)} > 0$才能保证 $B^{(k+1)}$也正定
- 即使$(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)} > 0$，也可能很小，容易产生较大的舍入误差

对称秩2修正

为克服秩1修正公式缺点，考虑$\Delta B^{(k)}$秩为2，设
$\Delta B^{(k)} = u^{(1)} (v^{(1)})^T + u^{(2)} (v^{(2)})^T$
带入拟Newton方程有
$B^{(k)} s^{(k)} + ((v^{(1)})^T s^{(k)}) u^{(1)} + ((v^{(2)})^T s^{(k)}) u^{(2)} = y^{(k)}$
类似的取
$\left \{ \begin{array}{l} u^{(1)} = y^{(k)} \\ (v^{(1)})^T s^{(k)} = 1 \end{array} \right.$ $\left \{ \begin{array}{l} u^{(2)} = -B^{(k)} s^{(k)} \\ (v^{(2)})^T s^{(k)} = 1 \end{array} \right.$
同秩1公式保持对称性推导，得到对称秩2修正公式/BFGS公式
$B^{(k+1)} = B^{(k)} - \frac {B^{(k)} s^{(k)} (s^{(k)})^T B^{(k)}} {(s^{(k)})^T B^{(k)} s^{(k)}} + \frac {y^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}}$

BFGS算法

类似同秩1修正算法，仅第4步使用对称秩2修正公式

Hesse逆修正

对称秩2修正

考虑直接构造近似于$(\triangledown^2 f(x^{(k)}))^{-1}$的矩阵$H^{(k)}$
这样无需求解线性方程组，直接计算
$d^{(k)} = -H^{(k)} \triangledown f(x^{(k)})$
相应拟Newton方程为
$H^{(k+1)} y^{(k)} = s^{(k)}$
可得$H^{(k)}$的对称秩1修正公式
$H^{(k+1)} = H^{(k)} + \frac {(s^{(k)} - H^{(k)} y^{(k)}) (s^{(k)} - H^{(k)} y^{(k)})T} {(s^{(k)} - H^{(k)} y^{(k)})^T y^{(k)}}$
可得$H^{(k)}$的对称秩2修正公式/DFP公式
$H^{(k+1)} = H^{(k)} - \frac {H^{(k)} y^{(k)} (y^{(k)})^T H^{(k)}} {(y^{(k)})^T H^{(k)} y^{(k)}} + \frac {s^{(k)} (s^{(k)})^T} {(s^{(k)})^T y^{(k)}}$

DFP算法

类似BFGS算法，只是

使用$H^{(k)}$计算更新方向
使用$H^{(k)}$的对称秩2修正公式修正

对正定二次函数，BFGS算法和DFP算法效果相同

对一般可微（非正定二次函数），一般认为BFGS算法在收敛性质、数值计算方面均由于DFP算法

Hesse逆的BFGS算法

考虑
$\begin{align*} B^{(k+1)} & = B^{(k)} + u^{(1)} (v^{(1)})^T + u^{(2)} (v^{(2)})^T \\ H^{(k+1)} & = (B^{(k+1)})^{-1} \\ & = (B^{(k)} + u^{(1)} (v^{(1)})^T + u^{(2)} (v^{(2)})^T)^{-1} \\ \end{align*}$
两次利用Sherman-Morrison公式，可得
$H^{(k+1)} = (I - \frac {s^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}}) H^{(k)} (I - \frac {s^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}})^T + \frac {s^{(k)} (s^{(k)})^T} {(y^{(k)})^T s^{(k)}}$

todo

还可以进一步展开
$H^{(k+1)} = H^{(k)} + (\frac 1 {(s^{(k)})^T y^{(k)}} + \frac {(y^{(k)})^T H^{(k)} y^{(k)}} {((s^{(k)})^T y^{(k)})^2}) s^{(k)} (s^{(k)})^T - \frac 1 {(s^{(k)})^T y^{(k)}} (H^{(k)} y^{(k)} (s^{(k)})^T + s^{(k)} (y^{(k)})^T H^{(k)})$

变度量法的基本性质

算法的下降性

定理1

设$B^{(k)}$（$H^{(k)}$）是正定对称矩阵，且有 $(s^{(k)})^T y^{(k)} > 0$，则由BFGS（DFS）公式构造的 $B^{(k+1)}$（$H^{(k+1)}$）是正定对称的

考虑$B^{(k)}$对称正定，有 $B^{(k)} = (B^{(k)})^{1/2} (B^{(k)})^{1/2}$
带入利用柯西不等式即可证

中间插入正定矩阵的向量内积不等式也称为广义柯西不等式

定理2

若$d^{(k)}$v是下降方向，且一维搜索是精确的，设 $B^{(k)}$（$H^{(k)}$）是正定对称矩阵，则有BFGS（DFP）公式构造的$B^{(k+1)}$（$H^{(k+1)}$）是正定对称的

精确一维搜索$(d^{(k)})^T \triangledown f(x^{(k+1)}) = 0$
则有$(s^{(k)})^T y^{(k)} > 0$

定理3

若用BFGS算法（DFP算法）求解无约束问题，设初始矩阵 $B^{(1)}$（$H^{(1)}$）是正定对称矩阵，且一维搜索是精确的，若$\triangledown f(x^{(k)}) \neq 0$，则产生搜索方向 $d^{(k)}$是下降方向

结合上2个结论，数学归纳法即可

总结

若每步迭代一维搜索精确，或满足$(s^{(k)})^T y^{(k)} > 0$
- 停止在某一稳定点
- 或产生严格递减的序列${f(x^{(k)})}$
若目标函数满足一定条件我，可以证明变度量法产生的点列 ${x^{(k)}}$收敛到极小点，且收敛速率超线性

搜索方向共轭性

用变度量法BFGS（DFP）算法求解正定二次函数

$$
min f(x) = \frac 1 2 x^T G x + r^T x + \sigma
$$

若一维搜索是精确的，假设已经进行了m次迭代，则

搜索方向$d^{(1)}, \cdots, d^{(m)}$是m个非零的G共轭方向

对于$j = 1, 2, \cdots, m$，有

$$
B^{(m+1)} s^{(j)} = y^{(j)}
(H^{(m+1)} y^{(j)} = s^{(j)})
$$

且$m = n$时有吧

$$
B^{(n+1)} = G(H^{(n+1)} = G^{-1})
$$

变度量法二次终止

若一维搜索是精确的，则变度量法（BFGS、DFP）具有二次终止

若$\triangle f(x^{(k)}) = 0, k \leq n$，则得到最优解 $x^{(k)}$
否则得到的搜索方向是共轭的，由扩展空间子定理， $x^{(n+1)}$是最优解

Posted 2019-03-26Updated 2021-07-19Probability2 minutes read (About 329 words)

概率不等式

Inequality

Azuma-Hoeffding Inequality

Azuma-Hoeffding 不等式：设 ${Xi:i=0,1,2,\cdots}$ 是鞅差序列，且 $|X_k - X{k-1}| < c_k$，则

$\begin{align*} super-martingale: P(X_N - X_0 \geq t) \leq exp \left ( \frac {-t^2} {2\sum^N_{k=1} c_k^2} \right ) \\ sub-martingale: P(X_N - X_0 \leq -t) \leq exp \left ( \frac {-t^2} {2\sum^N_{k=1} c_k^2} \right ) \\ martingale: P(|X_N - X_0| \geq t) \leq exp \left ( \frac {-t^2} {2\sum^N_{k=1} c_k^2} \right ) \end{align*}$

Hoeffding Inequality

Hoeffding 不等式：考虑随机变量序列 $X_1, X_2, \cdots, X_N, X_i \in [a_i, b_i]$

对随机变量 $\bar X = \frac 1 N \sum_{i=1}^N {X_i}$，对任意 $t>0$ 满足
$\begin{align*} P(\bar X - E \bar X \geq t) \leq exp(\frac {-2N^2t^2} {\sum_{i=1}^N (b_i - a_i)^2} ) \\ P(E \bar X - \bar X \geq t) \leq exp(\frac {-2N^2t^2} {\sum_{i=1}^N (b_i - a_i)^2} ) \\ \end{align*}$
对随机变量 $SN = \sum{i=1}^N X_i$，对任意 $t>0$ 满足
$\begin{align*} P(S_N - E S_N \geqslant t) & \leqslant exp \left ( \frac {-2t^2} {\sum_{i=1}^n (b_i - a_i)^2} \right ) \\ P(E S_N - S_N \geqslant t) & \leqslant exp \left ( \frac {-2t^2} {\sum_{i=1}^n (b_i - a_i)^2} \right ) \\ \end{align*}$

两不等式可用绝对值合并，但将不够精确

Bretagnolle-Huber-Carol Inequility

Bretagnolle-Huber-Carol 不等式：${X_i: i=1,2,\cdots,N} i.i.d. M(p1, p_2, \cdots, p_k)$ 服从类别为 $k$ 的多项分布

$p{\sum_{i=1}^k |N_i - Np_i| \geq \epsilon} \leq 2^k exp \left ( \frac {- n\epsilon^2} 2 \right )$

$N_i$：第 $i$ 类实际个数

Posted 2019-03-21Updated 2019-03-08C/C++ / Cstda few seconds read (About 0 words)