矩阵求导/矩阵微分

Layout Conventions

矩阵求导：在矩阵空间的多元微积分

• numerator layout：分子布局，微分分子的维数决定微分结果 的高维度结构（行优先，如：微分矩阵行数等于分子维数）
• denominator layout：分母布局，微分分母的维数为微分结果 的高维度结构（行优先）

• 两种布局方式相差转置
• 与微分分子、分母为行、或列向量无关 （即当微分分子、分母为向量时，行、列向量结果相同，只与 维度有关）
• 此布局模式仅讨论简单单因子微分时布局模式，复合多因子 应使用维度分析考虑 （即若严格按照计算规则，结果应该满足布局）

• 数分中Jaccobi行列式采用分子布局，以下默认为分子布局

维度分析

维度分析：对求导结果的维度进行分析，得到矩阵微分结果

• 维度一般化：将向量、矩阵维度置不同值，便于考虑转置
• 拆分有关因子：利用求导乘法公式（一般标量求导）拆分 因子，分别考虑各因子微分结果
• 变换微分因子、剩余因子（可能有左右两组），以满足矩阵运算 维度要求
  • 微分因子：按布局模式考虑维度、不转置
  • 剩余因子：为满足最终结果符合维度布局，考虑转置
  • 若维度一般化也无法唯一确定剩余因子形式，再考虑行、列 內积对应关系

• 考虑到矩阵乘法定义（左乘矩阵行数为乘法结果行数），则在 分子布局（分子行优先），简单微分中若微分因子为右乘矩阵、 剩余因子为左乘矩阵，则类似标量系数在前求微分，否则 结果需转置

例

• 考虑$\frac {\partial x^T A x} {\partial x}$，其中 $A \in R^{n*n}, x \in R^n$

• 维度一般化：$\frac {\partial u^T A v} {\partial x}$， 其中$A \in R^{a * b}, x \in R^n$

• 拆分有关因子，变换微分、剩余因子

  $$\begin{align*} \frac {\partial (u^T A) v} {\partial x} & = u^T A \frac {\partial v} {\partial x} \\ \frac {\partial u^T (A v)} {\partial x} & = v^T A^T \frac {\partial u} {\partial x} \end{align*}$$

• 则有

  $$\frac {\partial x^T A x} {\partial x} = x^T (A^T + A)$$

关于标量导数

标量对标量

标量$y$对标量$x$求导：$\frac {\partial y} {\partial x}$

向量对标量

向量$Y$关于标量$x$求导（$Y$为行、列向量均如此）

$$\frac {\partial Y} {\partial x} = \begin{bmatrix} \frac {\partial y_1} {\partial x} \\ \frac {\partial y_2} {\partial x} \\ \vdots \\ \frac {\partial y_n} {\partial x} \end{bmatrix}$$

矩阵对标量

矩阵$Y$关于标量$x$求导

$$\frac {\partial Y} {\partial x} = \begin{bmatrix} \frac {\partial y_{11}} {\partial x} & \frac {\partial y_{12}} {\partial x} & \cdots & \frac {\partial y_{1n}} {\partial x} \\ \frac {\partial y_{21}} {\partial x} & \frac {\partial y_{22}} {\partial x} & \cdots & \frac {\partial y_{2n}} {\partial x} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial y_{n1}} {\partial x} & \frac {\partial y_{n2}} {\partial x} & \cdots & \frac {\partial y_{nn}} {\partial x} \\ \end{bmatrix}$$

关于向量导数

标量对向量

标量$y$关于向量$X$求导

$$\frac {\partial y} {\partial X} = [\frac {\partial y} {\partial x_1}, \frac {\partial y} {\partial x_1}, \cdots, \frac {\partial y} {\partial x_n}]$$

向量对向量

向量$Y$关于向量$X$求导

$$\frac {\partial Y} {\partial X} = \begin{bmatrix} \frac {\partial y_1} {\partial x_1} & \frac {\partial y_1} {\partial x_2} & \cdots & \frac {\partial y_1} {\partial x_n} \\ \frac {\partial y_2} {\partial x_1} & \frac {\partial y_2} {\partial x_2} & \cdots & \frac {\partial y_2} {\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial y_m} {\partial x_1} & \frac {\partial y_m} {\partial x_2} & \cdots & \frac {\partial y_m} {\partial x_n} \end{bmatrix}$$

• $Y$、$X$为行、列向量均如此

关于矩阵导数

标量对矩阵求导

微分

微分形式

导数、微分转换

集合

势

• 等势：若集合 $X, Y$ 之间存在双射 $\phi: X \rightarrow Y$，则称 $X, Y$ 等势
• 可数/可列集合：与自然数集合、其子集等势的集合称为可数集合，否则称为不可数集合

• 等势构成集合之间的等价关系
  • 集合 $X$ 的等势类记为 $|X|$
  • 若存在单射 $\phi: X \rightarrow Y$，则记为 $|X| \leq |Y|$
• 一些基本结论
  • 自然数集 $N = {0, 1, 2, 3, \cdots}$ 和闭区间 $[0,1]$ 不等势

• https://zhuanlan.zhihu.com/p/34097692

序

• 偏序集：若集合 $A$ 上有二元关系 $\leq$ 满足以下性质，则称集合 $A$ 为偏序集，关系 $\leq$ 称为偏序关系

  • 反身性：$\forall x \in A, x \leq x$
  • 传递性：$(x \leq y) \wedge (y \leq z) \Rightarrow x \leq z$
  • 反称性：$(x \leq y) \wedge (y \leq x) \Rightarrow x = y$

• 全序集：若 $\leq$ 是集合上的偏序关系，若对每个$x, y \in A$，必有 $x\leq y$ 或 $y \leq x$，则称集合 $A$ 为全序集，关系 $\leq$ 为全序关系

• 良序集：若集合 $A$ 每个自己都有极小元，则称为良序集

• 特点
  • 偏序指集合中只有部分成员之间可比较
  • 全序指集合全体成员之间均可比较
  • 良序集则是不存在无穷降链的全序集（可有无穷升链）

序数

• 序数：若集合 $A$ 中每个元素都是 $A$ 的子集，则称 $A$ 是传递的。而 $A$ 对于关系 $\in$ 构成良序集，则称 $A$ 为序数

• 满足如下形式的集合即为序数

  $$\{\phi, \{\phi\}, \{\phi, \{\phi\}\}, \{\phi, \{\phi\}, \{\phi, \{\phi\}\}\} \}, \cdots$$

• 序数的性质（引理）

  • 若 $\alpha$ 为序数，$\beta \in \alpha$，则 $\beta$ 也是序数
  • 对任意序数 $\alpha, \beta$，若 $\alpha \subset \beta$，则 $\alpha \in \beta$
  • 对任意序数 $\alpha, \beta$，必有 $\alpha \subseteq \beta$ 或 $\beta \subseteq \alpha$

• 由以上，序数性质的解释

  • 序数是唯一的，都满足上述形式
  • 序数都是由自己之前的所有序数构造而来
  • 对任意序数 $\alpha$，有 $\alpha = {\beta: \beta < \alpha }$ （$ < $ 表示偏序关系）

• 将 $0, 1, 2, \cdots$ 依次对应上述序数，即给出自然数和序数

  $$0 := \phi, 1 := \{phi\}, 2 := \{\phi, \{phi\}\}, \cdots$$

• https://zh.wikipedia.org/wiki/%E5%BA%8F%E6%95%B0
• 自然数可用于描述集合大小（势，基数）、序列中元素的位置（序，序数）

良序定理

• Zermelo 良序定理：任何集合 $P$ 都能被赋予良序

• Zermelo 良序定理和 ZFC 选择公理等价，可以由选择公理证明
  • 由选择公理，可以一直从集合中选择元素，建立偏序关系
  • 而集合有限，则集合和序数之间可以建立双射

基

基数

• 基数：序数 $k$ 为基数，若对任意序数 $\lambda < k$，都有 $|\lambda| < |k|$
• Counter 定理：设 $A$ 为集合，$P(A)$ 为 $A$ 的幂集，则有 $|A| \leq |P(A)|$

• 基数是集合势的标尺

• 数的集合的基数

  • 自然数集合基数 $\aleph_0$：最小的无限基数
  • 实数集集合基数称为 continuum 连续统

• 连续统假设：不存在一个集合，基数在自然数集和连续统之间

  • 哥德尔证明：连续统假设与公理化集合论体系 Zermelo-Fraenkel set theory with the axiom of choice 中不矛，即不能再 ZFC 中被证伪
  • 科恩证明：连续统假设和 ZFC 彼此独立，不能在 ZFC 公理体系内证明、证伪

• https://zh.wikipedia.org/wiki/%E5%9F%BA%E6%95%B0_(%E6%95%B0%E5%AD%A6)

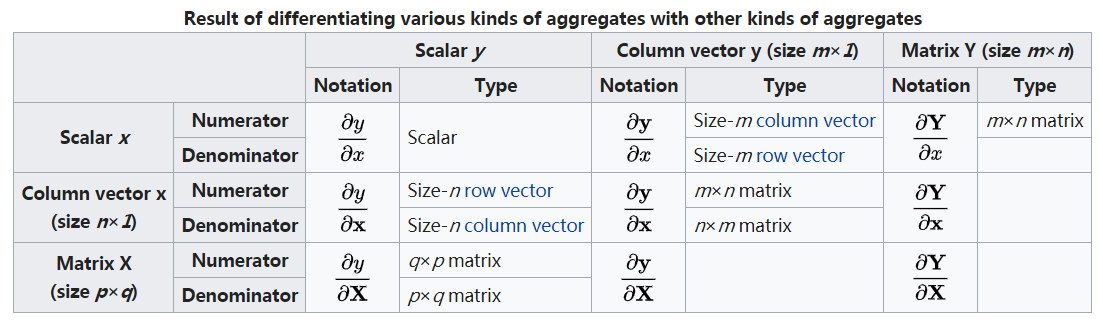
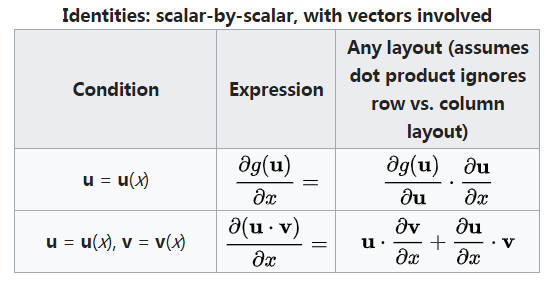
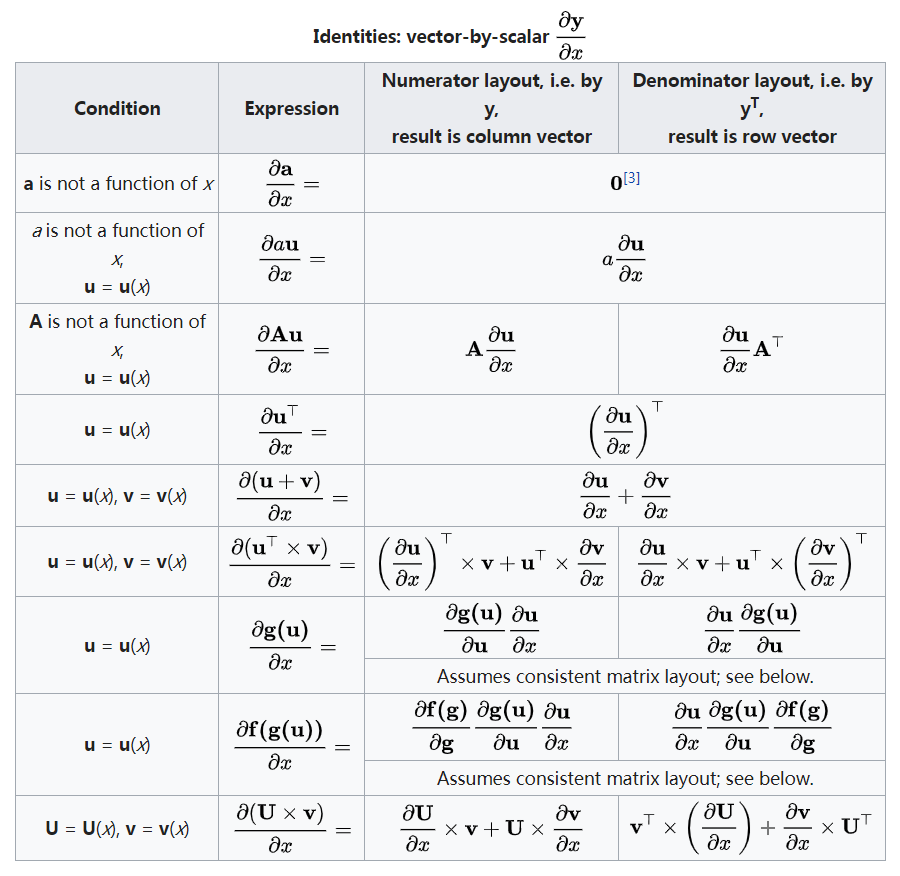
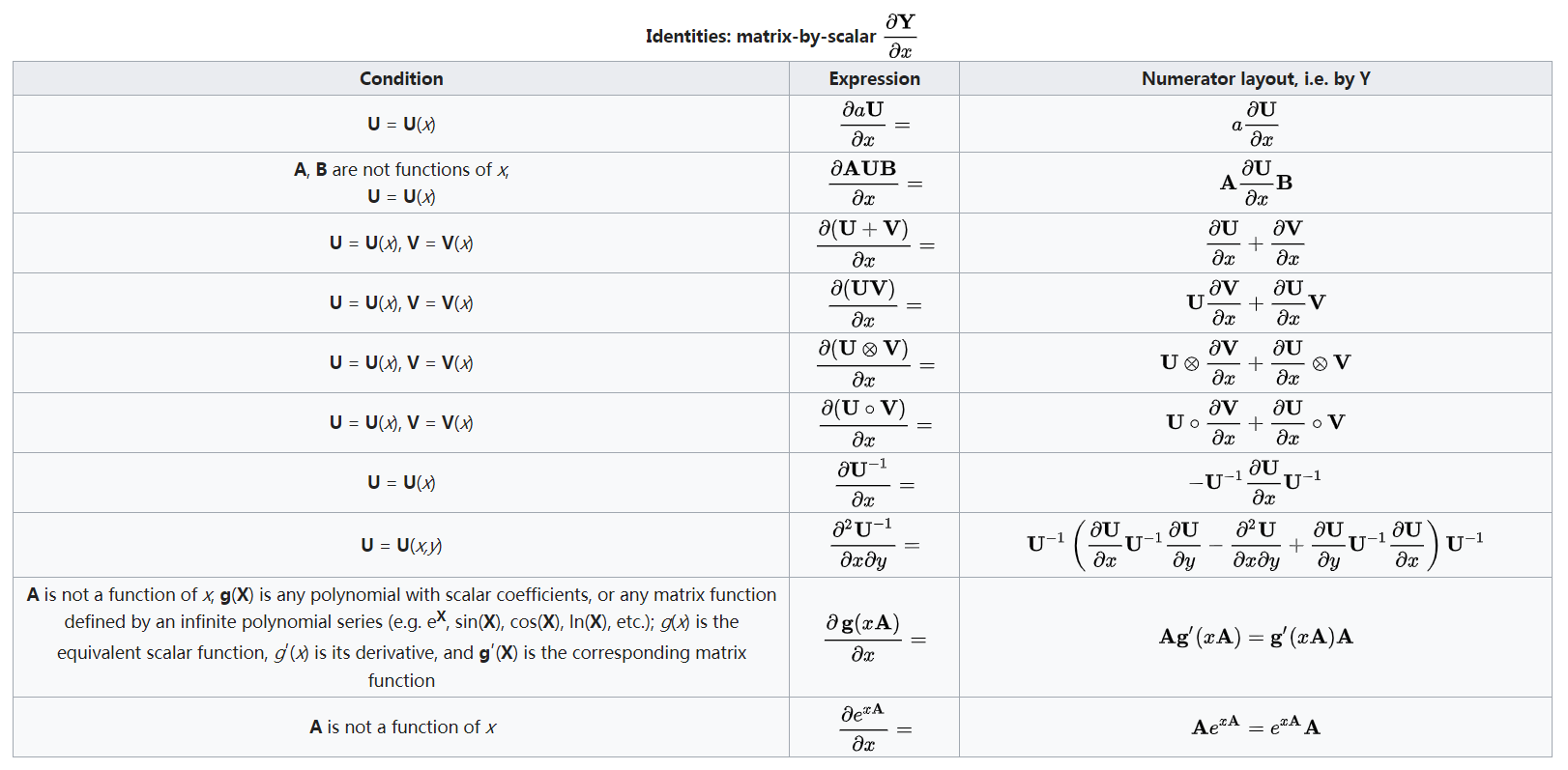
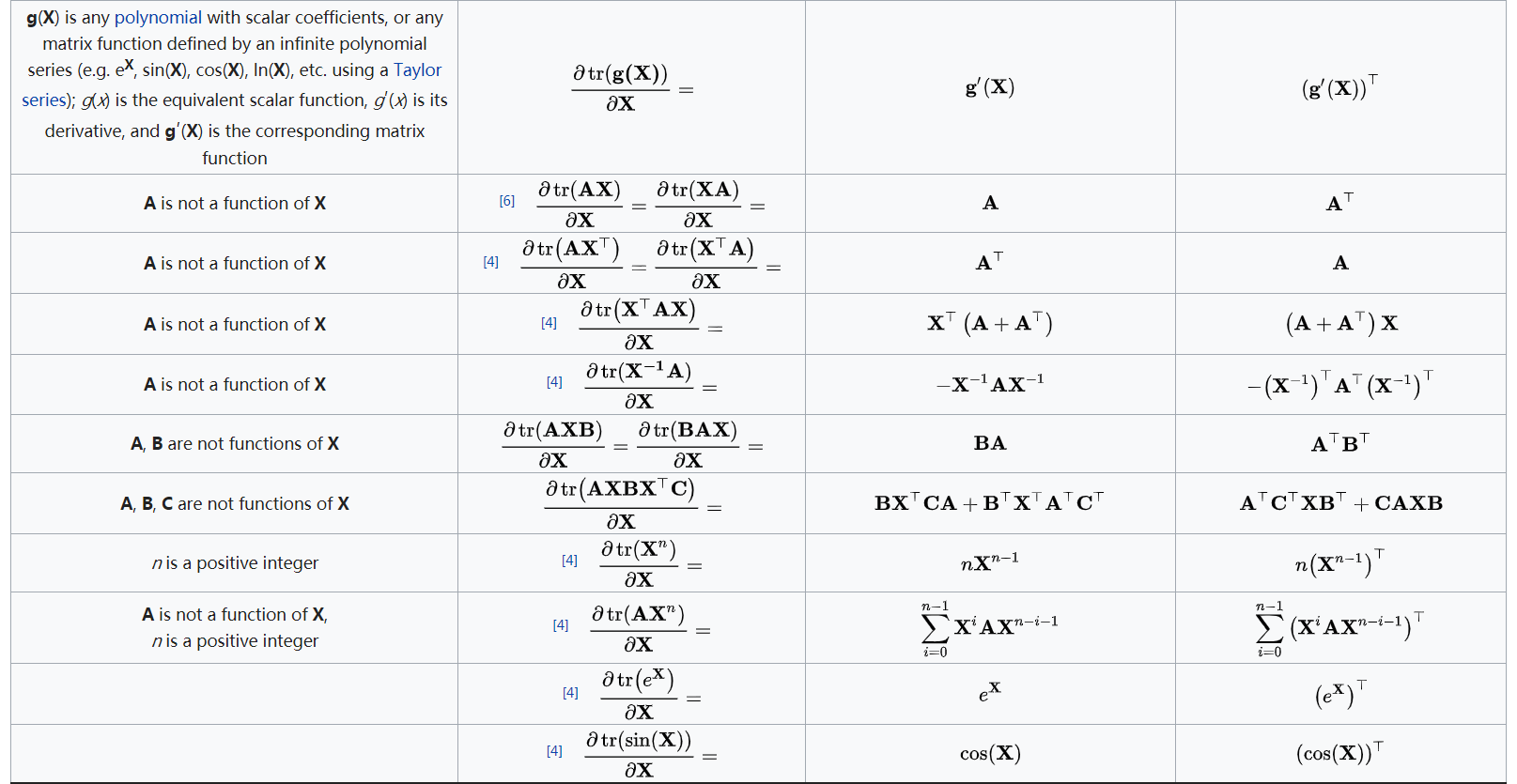
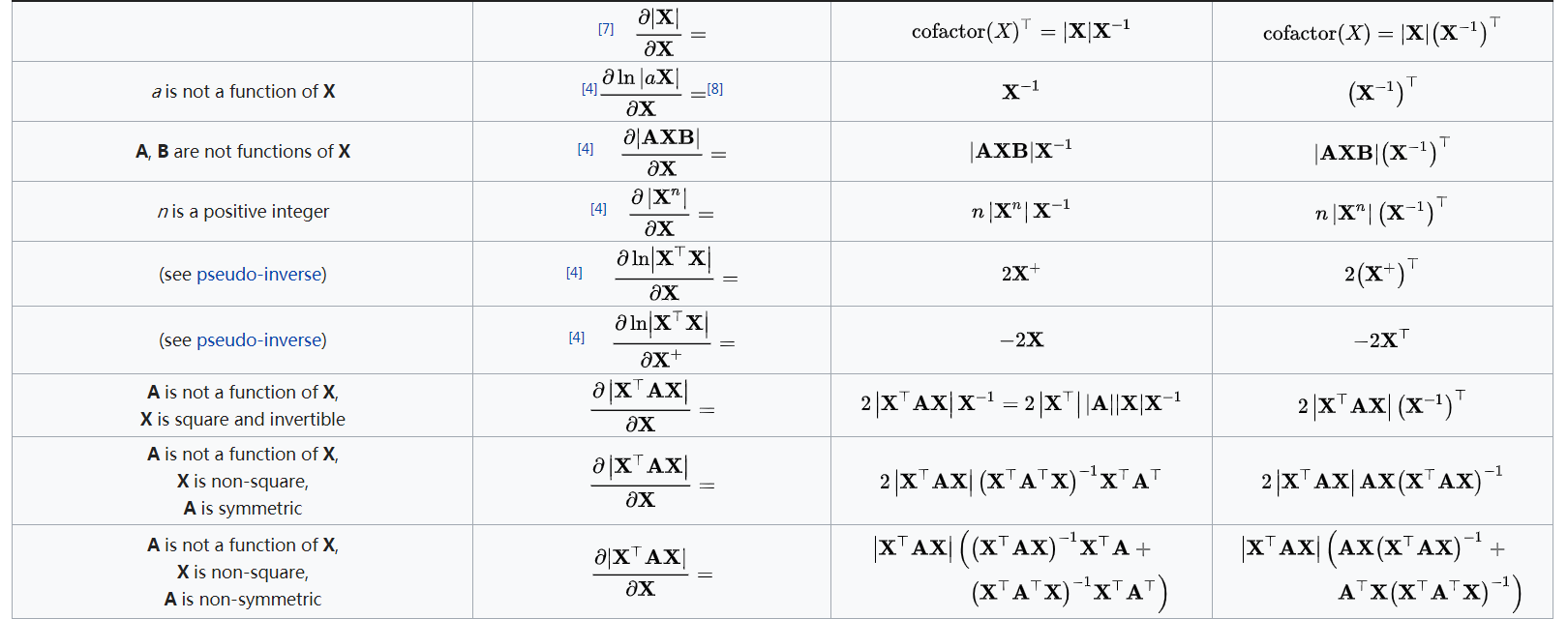
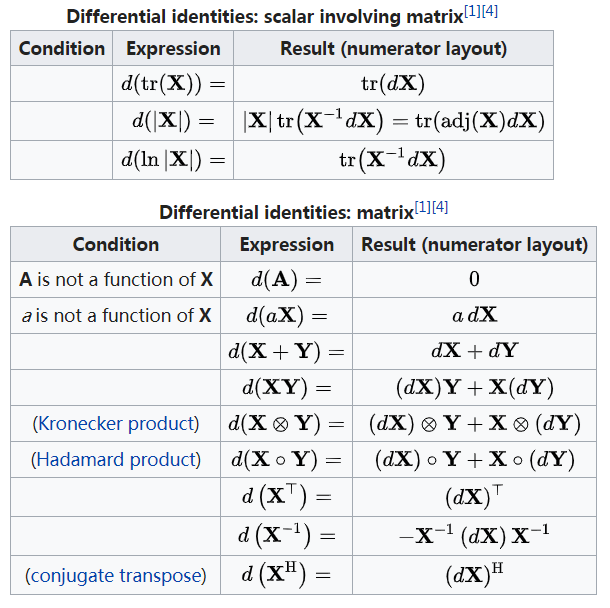
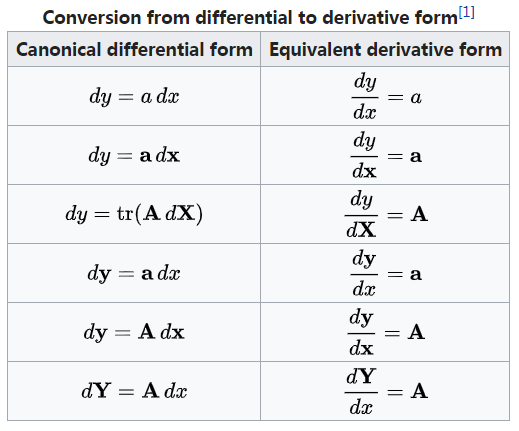
距离

• 距离可认为是两个对象 $x,y$ 之间的 相似程度
  • 距离和相似度是互补的
  • 可以根据处理问题的情况，自定义距离

Bregman Divergence

$$D(x, y) = \Phi(x) - \Phi(y) - <\nabla \Phi(y), (x - y)>$$

• $Phi(x)$：凸函数

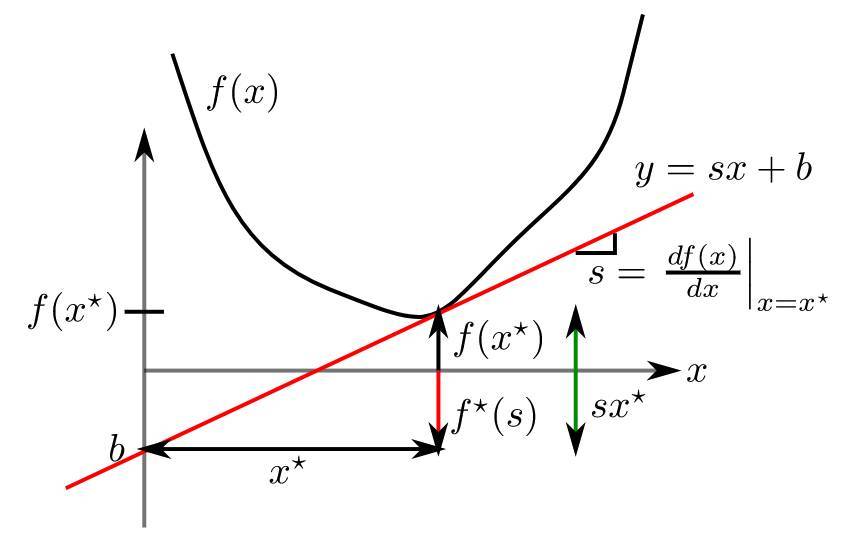
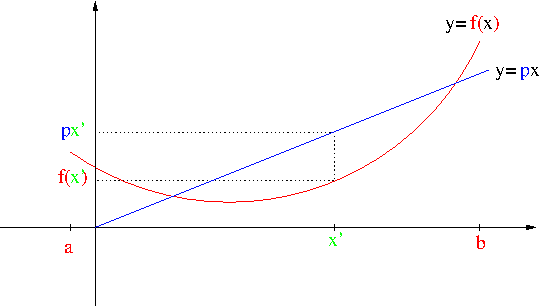
• 布雷格曼散度：穷尽所有关于“正常距离”的定义

  • 给定 $R^n * R^n \rightarrow R$ 上的正常距离 $D(x,y)$，一定可以表示成布雷格曼散度形式
  • 直观上：$x$处函数、函数过$y$点切线（线性近似）之差
    • 可以视为是损失、失真函数：$x$由$y$失真、近似、添加噪声得到

• 特点

  • 非对称：$D(x, y) = D(y, x)$
  • 不满足三角不等式：$D(x, z) \leq D(x, y) + D(y, z)$
  • 对凸集作 Bregman Projection 唯一
    • 即寻找凸集中与给定点Bregman散度最小点
    • 一般的投影指欧式距离最小

• 正常距离：对满足任意概率分布的点，点平均值点（期望点）应该是空间中距离所有点平均距离最小的点
• 布雷格曼散度对一般概率分布均成立，而其本身限定由凸函数生成

  • 和 Jensen 不等式有关？凸函数隐含部分对期望的度量

• http://www.jmlr.org/papers/volume6/banerjee05b/banerjee05b.pdf

单点距离

Minkowski Distance

闵科夫斯基距离：向量空间 $\mathcal{L_p}$ 范数

$$d_{12} = \sqrt [1/p] {\sum_{k=1}^n |x_{1,k} - x_{2,k}|^p}$$

• 表示一组距离族

  • $p=1$：Manhattan Distance，曼哈顿距离
  • $p=2$：Euclidean Distance，欧式距离
  • $p \rightarrow \infty$：Chebychev Distance，切比雪夫距离

• 闵氏距离缺陷

  • 将各个分量量纲视作相同
  • 未考虑各个分量的分布

Mahalanobis Distance

马氏距离：表示数据的协方差距离

$$d_{12} = \sqrt {({x_1-\mu}^T) \Sigma^{-1} (x_2-\mu)}$$

• $\Sigma$：总体协方差矩阵

• 优点
  • 马氏距离和原始数据量纲无关
  • 考虑变量相关性
• 缺点
  • 需要知道总体协方差矩阵，使用样本估计效果不好

LW Distance

兰氏距离：Lance and Williams Distance，堪培拉距离

$$d_{12} = \sum^{n}_{k=1} \frac {|x_{1,k} - x_{2,k}|} {|x_{1,k} + x_{2,k}|}$$

• 特点
  • 对接近0的值非常敏感
  • 对量纲不敏感
  • 未考虑变量直接相关性，认为变量之间相互独立

Hamming Distance

汉明距离：差别

$$diff = \frac 1 p \sum_{i=1}^p (v^{(1)}_i - v^{(2)}_i)^k$$

• $v_i \in {0, 1}$：虚拟变量
• $p$：虚拟变量数量

• 可以衡量定性变量之间的距离

Embedding

• 找到所有点、所有维度坐标值中最大值 $C$
• 对每个点 $P=(x_1, x_2, \cdots, x_d)$
  • 将每维 $x_i$ 转换为长度为 $C$ 的 0、1 序列
  • 其中前 $x_i$ 个值为 1，之后为 0
• 将 $d$ 个长度为 $C$ 的序列连接，形成长度为 $d * C$ 的序列

• 以上汉明距离空间嵌入对曼哈顿距离是保距的

Jaccard 系数

Jaccard 系数：度量两个集合的相似度，值越大相似度越高

$$sim = \frac {\|S_1 \hat S_2\|} {\|S_1 \cup S_2\|}$$

• $S_1, S_2$：待度量相似度的两个集合

Consine Similarity

余弦相似度

$$similarity = cos(\theta) = \frac {x_1 x_2} {\|x_1\|\|x_2\|}$$

• $x_1, x_2$：向量

欧式距离

点到平面

• $T={(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$：样本点集
• $wx + b = 0$：超平面

Functional Margin 函数间隔

$$\hat{\gamma_i} = y_i(wx_i + b)$$

• 函数间隔可以表示分类的正确性、确信度

  • 正值表示正确
  • 间隔越大确信度越高

• 点集与超平面的函数间隔取点间隔最小值 $\hat{T} = \min_{i=1,2,\cdots,n} \hat{\gamma_i}$

• 超平面参数 $w, b$ 成比例改变时，平面未变化，但是函数间隔成比例变化

Geometric Margin 几何间隔

$$\begin{align*} \gamma_i & = \frac {y_i} {\|w\|} (wx_i + b) \\ & = \frac {\hat \gamma_i} {\|w\|} \end{align*}$$

• 几何间隔一般是样本点到超平面的 signed distance

  • 点正确分类时，几何间隔就是点到直线的距离

• 几何间隔相当于使用 $|w|$ 对函数间隔作规范化

  • $|w|=1$ 时，两者相等
  • 几何间隔对确定超平面、样本点是确定的，不会因为超平面表示形式改变而改变

• 点集与超平面的几何间隔取点间隔最小值 $\hat{T} = \min_{i=1,2,\cdots,n} \hat{\gamma_i}$

Levenshtein/Edit Distance

（字符串）编辑距离：两个字符串转换需要进行插入、删除、替换操作的次数

$$lev_{A,B}(i, j) = \left \{ \begin{array}{l} i, & j = 0 \\ j, & i = 0 \\ min \left \{ \begin{array}{l} lev_{A,B}(i,j-1) + 1 \\ lev_{A,B}(i-1,j) + 1 \\ lev_{A,B}(i-1, j-1) + 1 \end{array} \right. & A[i] != B[j] \\ min \left \{ \begin{array}{l} lev_{A,B}(i,j-1) + 1 \\ lev_{A,B}(i-1,j) + 1 \\ lev_{A,B}(i-1, j-1) \end{array} \right. & A[i] = B[j] \\ \end{array} \right.$$

组间距离

Single Linkage

Average Linkage

Complete Linkage

Reproducing Kernel Hilbert Space

• Hilbert space：假设 $K(x,z)$ 是定义在 $\mathcal{X X}$ 上的对称函数，并且对任意 $x_1, x_2, \cdots, x_m \in \mathcal{X}$，$K(x,z)$ 关于其的 Gram* 矩阵半正定，则可以根据函数 $K(x,z)$ 构成一个希尔伯特空间

构造步骤

定义映射构成向量空间

• 定义映射

  $$\phi: x \rightarrow K(·, x)$$

• 根据此映射，对任意 $x_i \in \mathcal{X}, \alpha_i \in R, i = 1,2,\cdots,m$ 定义线性组合

  $$f(·) = \sum_{i=1}^m \alpha_i K(·, x_i)$$

• 由以上线性组合为元素的集合 $S$ 对加法、数乘运算是封闭的，所以 $S$ 构成一个向量空间

定义内积构成内积空间

• 在 $S$ 上定义运算 $ * $：对任意 $f,g \in S$

  $$\begin{align*} f(·) = \sum_{i=1}^m \alpha_i K(·, x_i) \\ g(·) = \sum_{j=1}^n \beta_j K(·, z_j) \end{align*}$$

  定义运算 $ * $

  $$f * g = \sum_{i=1}^m \sum_{j=1}^n \alpha_i \beta_j K(x_i, z_j)$$

• 为证明运算 $ * $ 是空间 $S$ 的内积

  • 需要证明：
    • $(cf) g = c(f g), c \in R$
    • $(f + g) h = f h + g * h, h \in S$
    • $f g = g f$
    • $f f \geq 0, f f = 0 \Leftrightarrow f = 0$
  • 其中前3条由 $S$ 元素定义、$K(x,z)$ 对称性容易得到
  • 由 $ * $ 运算规则可得 $$f * f = \sum_{i,j=1}^m \alpha_i \alpha_j K(x_i, x_j)$$ 由 Gram 矩阵非负可知上式右端非负，即 $f * f \geq 0$

• 为证明 $f * f \Leftrightarrow f = 0$

  • 首先证明

    $$|f * g|^2 \leq (f * f)(g * g)$$

    • 设$f, g \in S$，则有$f + \lambda g \in S$，则有

      $$\begin{align*} (f + \lambda g) * (f + \lambda g) & \geq 0 \\ f*f + 2\lambda (f * g) + \lambda^2 (g*g) & \geq 0 \end{align*}$$

    • 则上述关于$\lambda$的判别式非负，即

      $$(f*g)^2 - (f*f)(g*g) \leq 0$$

  • $\forall x \in \mathcal{x}$，有

    $$K(·, x) * f = \sum_{i=1}^m \alpha_i K(x, x_i) = f(x)$$

    则有

    $$|f(x)|^2 = |K(·, x) * f|^2$$

  • 又

    $$|K(·, x) * f|^2 \leq (K(·, x) * K(·, x))(f * f) = K(x, x)(f*f)$$

    则有

    $$|f(x)|^2 \leq K(x, x) (f * f)$$

    即$f * f = 0$时，对任意$x$都有$|f(x)| = 0$

• 因为 $ * $ 为向量空间 $S$ 的内积，可以继续用 $ · $ 表示

  $$f·g = \sum_{i=1}^m \sum_{j=1}^n \alpha_i \alpha_j K(x_i,z_J)$$

完备化构成Hilbert空间

• 根据内积定义可以得到范数

  $$\|f\| = \sqrt {f · f}$$

  所以 $S$ 是一个赋范向量空间，根据泛函分析理论，对于不完备的赋范空间 $S$ ，一定可以使之完备化得到希尔伯特空间 $\mathcal{H}$

• 此希尔伯特空间 $\mathcal{H}$ ，称为 reproducing kernel Hilber Space ，因为核 $K$ 具有再生性

  $$\begin{align*} K(·, x) · f & = f(x) \\ K(·, x) · K(·, Z) & = K(x, z) \end{align*}$$

Positive Definite Kernel Function

• 设 $K: \mathcal{X X} \leftarrow R$ 是对称函数，则 $K(x,z)$ 为正定核函数的充要条件是 $\forall x_i \in \mathcal{X}, i=1,2,…,m$，$K(x,z)$ 对应的 Gram 矩阵 $K = [K(xi, x_j)]{mm} $ 是半正定矩阵

• 必要性

• 由于 $K(x,z)$ 是 $\mathcal{X X}$ 上的正定核，所以存在从 $\mathcal{X}$ 到 Hilbert* 空间 $\mathcal{H}$ 的映射，使得

  $$K(x,z) = \phi(x) \phi(z)$$

• 则对任意 $x_1, x_2, \cdots, x_m$，构造 $K(x,z)$ 关于其的 Gram 矩阵

  $$[K_{ij}]_{m*m} = [K(x_i, x_i)]_{m*m}$$

• 对任意 $c_1, c_2, \cdots, c_m \in R$，有

  $$\begin{align*} \sum_{i,j=1}^m c_i c_j K(x_i, x_j) & = \sum_{i,j=1}^m c_i c_j (\phi(x_i) \phi(x_j)) \\ & = (\sum_i c_i \phi(x_i))(\sum_j c_j \phi(x_j)) \\ & = \| \sum_i c_i \phi(x_i) \|^2 \geq 0 \end{align*}$$

  所以 $K(x,z)$ 关于 $x_1, x_2, \cdots, x_m$ 的 Gram 矩阵半正定

• 充分性

• 对给定的 $K(x,z)$，可以构造从 $\mathcal{x}$ 到某个希尔伯特空间的映射

  $$\phi: x \leftarrow K(·, x)$$

• 且有

  $$K(x,z) = \phi(x) · \phi(z)$$

  所以 $K(x,z)$ 是 $\mathcal{X * X}$ 上的核函数

Legendre Transformation

勒让德变换：用 $f^{ * }(p)$ 表示凸、可导函数 $f(x)$ 的变换，其中 $p$ 是 $f(x)$ 导数

$$f^{*}(p) = p^T x - f(x)|_{\frac {d(p^T x - f(x))} {dx} = 0}$$

• $x$：参数，满足 $\frac {d(p^T x - f(x))} {dx} = 0$，随 $p$ 取值改变
• 可导：有导数；凸：导数唯一

• 勒让德变换是实变量的实值凸函数的对合变换
  • 把定义在线性空间上的函数变换至对偶空间的函数
  • 是点、（切）线之间对偶关系的应用
    • 严格凸函数中，切线、导数一一对应
    • 函数关系 $f(x)$ 可使用 $(x, y=f(x))$ 点集表示，也可用切线集合表示

• involution 对合：对合函数 $f$ 的反函数的为自身，即 $f(f(x))=x$；对合线性变换 $V$ 满足 $V^2 = E$

Legendre 变换理解（按 Fenchel 共轭）

• $f^{*}(p)$：可理解为斜率为 $p$、同 $f(x)$ 有交点 $x_0$ 的直线在零点处值（截距）和 $f(x_0)$ 的最大差

  

• $x$：可以理解为函数 $f(x)$ 上距离给定斜率为 $p$、过原点的直线 $f(x)=px$ 竖直距离最大的点

  

  • 类似一个端点为 $0$ 的 Bregman 散度

• Legendre 变换为对合变换，进行两次的变换得到原函数

  

  $$\begin{align*} f^{**}(x) & = \sup_{p \in dom(f^{*})} [x^T p - f^{*}(p)] \\ & = \sup_{u \in dom(f)}[x^T \nabla f(u) - \nabla f(u)^T u + f(u)] \\ & = \sup_{u \in dom(f)}[f(u) + \nabla f(u)^T (x-u)] \\ & = f(x) \end{align*}$$

• 若视凸函数 $f(x)$ 视为积分，则其共轭 $f^{ * }(x)$ 为对另一轴积分，二者导函数互为反函数

  $$f(x) + f^{*}(p) = xp, p = \frac {df(x)} {dx}$$

• 以上性质均按 Fenchel 共轭，但要求 $f(x)$ 为凸、可导函数，故等价于 Legendre 变换

Legendre 变换最大值式定义

$$\begin{align*} L(p, x) &= px - f(x) \\ \frac {\partial (px - f(x))} {\partial x} &= p - \frac {df(x)} {dx} = 0 \\ \Rightarrow & p = \frac {df(x)} {dx} \end{align*}$$

• Legendre 变换可以视为寻找 $px-f(x)$ 最大值（如前述）
  • $f(x)$ 为凸函数，则 $p=\frac {df(x)} {dx}$ 是最大值点
  • 则将 $f(x)$ 导函数的反函数 $x=f^{-1}(p)$ 带入即可

Legendre 变换数学性质

• 标度性质

  $$\begin{align*} f(x) & = a g(x) \rightarrow f^{*}(p) = a g^{*}(\frac p a) \\ f(x) & = g(ax) \rightarrow f^{*}(p) = g^{*}(\frac p a) \end{align*}$$

  由此，$r$次齐次函数的勒让德变换是$s$次齐次函数，满足

  $$\frac 1 r + \frac 1 s = s$$

• 平移性质

  $$\begin{align*} f(x) & = g(x) + b \rightarrow f^{*}(p) = g^{*}(p) - b f(x) & = g(x+y) \rightarrow f*^{*}(p) = g^{*}(p) - py \end{align*}$$

• 反演性质

  $$f(x) = g^{-1}(x) \rightarrow f^{*}(p) = -p g^{*}(\frac 1 p)$$

• 线性变换性质

  $$(Af)^{*} = f^{*}A^{*}$$

  • $f$：$R^n$上的凸函数
  • $A$：$R^n \rightarrow R^m$的线性变换
  • $A^{}: <Ax, y^{}> = $：$A$伴随算子

Fenchel Conjugate / 凸共轭

$$f^{*}(p) = \sup_{x \in R}{p^Tx - f(x)}$$

• Fenchel 共轭是对 Legendre 变换的扩展，不再局限于凸、可导函数
  • Fenchel 共轭可类似 Legendre 理解，但是适用范围更广
  • 对凸函数 Fenchel 共轭的共轭即为原函数，对非凸函数 Fenchel 共轭得到原函数凸包
  • 用罗尔中值定理描述极值、导数关系：兼容 Legendre 变换中导数支撑面

• 非凸函数线性外包络是凸函数

Fenchel-Young不等式

$$f(x) + f^{*}(p) \geq <p, x>$$

• 证明

  $$\begin{align*} f(x) + f^{*}(p) & = f(x) + \sup_{x \in dom(f)} {(x^T p - f(x))} \\ & \geq f(x) + x^T p - f(x) = x^T p \end{align*}$$

• 按积分理解，仅$p$为$x$共轭时取等号

  

Fenchel Conjugate 推导 Lagrange Duality

• 原问题 Prime

  $$\begin{align*} & \min {f(x)} \\ s.t. & g(x) \leq 0 \\ \end{align*}$$

• 约束条件 $g(x) \leq 0$ 扰动函数化、求 Fenchel 共轭

  $$\begin{align*} p(u) & = \inf_{x \in X, g(x) \leq u} f(x) \\ p^{*}(y) & = \sup_{y \in R^r} \{u^T y - p(u)\} \end{align*}$$

• 记 $\lambda = -y$，并将 $y=-\lambda$ 带入 $-p^{*}(y)$ 中得到

  $$\begin{align*} -p^{*}(y) & = \inf_{u \in R^r} \{p(u) - u^T y\} \\ d(\lambda) & = \inf_{u \in R^r} \{p(u) + u^T \lambda\} \\ & = \inf_{u \in R^r} \{\inf_{x \in X, g(x) \leq u} f(x) + \lambda^T u\} \end{align*}$$

  • $\lambda = -y$

• 将 $\inf_{x \in X, g(x) \leq u}$ 外提，并考虑到约束 $g(x) \leq u$（即 $u \geq g(x)$），则

  $$\begin{align*} \lambda \geq 0 & \Rightarrow \lambda^T g(x) \leq \lambda u \\ d(\lambda) & = \left \{ \begin{array}{l} \inf_{x \in X} \{f(x) + \lambda^T g(x)\}, & \lambda \geq 0 \\ -\infty, & otherwise \end{array} \right. \end{align*}$$

• 考虑 Fenchel 不等式

  $$\begin{align*} p(u) + p^{*}(-y) & \geq u^T (-y) \\ p(0) + p^{*}(-y) & \geq 0 \\ p(0) & \geq -p^{*}(-y) \\ p(0) & \geq d(\lambda) \end{align*}$$

• 则可得 Lagrange 对偶 Prime、Dual 最优关系

  $$L(x, \lambda) = f(x) + \lambda^T g(x), \lambda \geq 0 \\ D^{*} := \max_{\lambda \geq 0} \min_x L(x, \lambda) \leq \min_x \max_{\lambda \geq 0} L(x, \lambda) =: P^{*}$$

  

Lagrange Duality 推导 Fenchel 对偶

• Fenchel 对偶可以视为 Lagrange 对偶的应用

• 原问题、等价问题

  $$\begin{align*} & \min_x & f(x) - g(x) \\ \Leftrightarrow & \min_{x,z} & f(x) - g(z) \\ & s.t. & x = z \end{align*}$$

• 对上式取 Lagrange 对偶 $L(u)$、等价得到

  $$\begin{align*} L(u) &= \min_{x,z} f(x) - g(z) + u^T(z-x) \\ &= -(f^{*}(u) - g^{(-u)}) \end{align*}$$

• Fenchel 对偶：寻找截距差值最大的平行切线

Fourier Transformation

（连续）傅里叶变换：将时域映射到频域的变换

$$F(\xi) = \int_{-\infty}^{+\infty} f(x) e^{-2\pi ix \xi} dx$$

• $x$：自变量，多表示时间
• $F(\xi)$：频率

傅里叶变换理解

• 将自变量 $x$ 线性映射为极坐标系中角度，调整线性映射的比例（即频率），即可绘制出不同的曲线

  

• 计算不同频率下曲线围成的图像的质心（径向）坐标

  • 质心的角度坐标只需原函数沿 $x$ 轴平移即可改变
  • 若原图像不关于 $x$ 轴对称，则质心在频率 0 点处有较大值

  

• 据以上：周期函数映射在极坐标系下图像，其质心位置在对应频率下取波峰值

• https://charlesliuyx.github.io/2018/02/18/%E3%80%90%E7%9B%B4%E8%A7%82%E8%AF%A6%E8%A7%A3%E3%80%91%E8%AE%A9%E4%BD%A0%E6%B0%B8%E8%BF%9C%E5%BF%98%E4%B8%8D%E4%BA%86%E7%9A%84%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2%E8%A7%A3%E6%9E%90/

傅里叶变换计算

• 利用复数项 $e^{-2\pi ix \xi}$ 表示在复平面中的旋转角度

  • $x$ 为函数自变量，$\xi$ 为频率（即自变量映射比例）
  • 傅里叶变换中旋转为缺省为顺时针，所以补足负号
  • 函数在复平面中则表示为 $f(x) e^{-2\pi ix \xi}$

• 函数围成的曲线质心则为 $\frac 1 {x2 - x_1} \int{x_1}^{x_2} f(x) e^{-2\pi ix \xi} dx$

  • 系数 $\frac 1 {x_2 - x_1}$ 将积分结果放缩回质心，可省略
  • 将原积分区域外函数值定为 0，积分上下限扩展至 $-\infty, \infty$ 不影响积分结果
  • 函数有效取值部分越长，质心波动约迅速

傅里叶变换

Discrete Fourier Transformation

DFT：归一化二维离散傅里叶变换

$$\begin{align*} F(u,v) & = \frac 1 {\sqrt{NM}} \sum_{x=0}^{N-1} \sum_{y=0}^{M-1} f(x,y) e^{-\frac {2\pi i} N ux} e^{-\frac {2\pi i} M vy} \\ f(x,y) & = \frac 1 {\sqrt{NM}} \sum_{u=0}^{N-1} \sum_{v=0}^{M-1} F(u,v) e^{\frac {2\pi i} N ux} e^{\frac {2\pi i} M vy} \\ \end{align*}$$

Discrete Consine Transformation

余弦变换

• 在给定区间为满足狄利克雷条件的连续实对称函数，可以展开为 仅含余弦项的傅里叶级数

• 对于定义在正实数域上的函数，可以通过偶延拓、或奇延拓满足 上述条件

离散余弦变换

• $(x,y) or (u,v) = (0,0)$时

  $$\begin{align*} F(u,v) & = \frac 1 N \sum_{x=0}^{N-1} \sum_{y=0}^{N-1} f(x,y) cos[\frac \pi N u(x + \frac 1 2)] cos[\frac \pi N v(y + \frac 1 2)] \\ f(x,y) & = \frac 1 N \sum_{u=0}^{N-1} \sum_{v=0}{N-1} F(u,v) cos[\frac \pi N u(x + frac 1 2)] cos[\frac \pi N v(y + \frac 1 2)] \end{align*}$$

• 其他

  $$\begin{align*} F(u,v) & = \frac 1 {2N} \sum_{x=0}^{N-1} \sum_{y=0}^{N-1} f(x,y) cos[\frac \pi N u(x + \frac 1 2)] cos[\frac \pi N v(y + \frac 1 2)] \\ f(x,y) & = \frac 1 {2N} \sum_{u=0}^{N-1} \sum_{v=0}{N-1} F(u,v) cos[\frac \pi N u(x + frac 1 2)] cos[\frac \pi N v(y + \frac 1 2)] \end{align*}$$

Projected Gradient Descent

受限优化问题

$$\min_{x \in C} f(x)$$

• $C \subseteq R^d$：受限凸集

投影梯度下降：采用后处理的方式，将迭代位置拉回到约束条件内

• 使用一般下降算法进行位置更新，新位置$x_{t+1}^{‘}$可能 不再满足约束条件

• 为使新位置$x{t+1}^{‘}$符合受限集合，可以选择在$L_2$范数 下距离受限集合$C$最近的的点 $x{t+1}=\arg\min{x \in C} |x - x{t+1}^{‘}|$作为下步 真正迭代位置

线性约束

Projection Matrix

• 投影矩阵：矩阵$P \in R^{n*n}$，若满足$P^T = P, P^2 = P$
• 若$A \in R^{m*n}$为行满秩矩阵，则$A$的零空间为 $L_A = {x \in R^{n} | Ax = 0}$，对应正交空间为 $L_A^{\perp} = {A^T y | y \in R^m}$

对$\forall x \in R^n$进行正交分解

$$\begin{align*} \forall x \in R^n, x & = x_1 + x_2, x_1 \in L_A, x_2 \in L_A^{\perp} \\ x_1 & = P_A x \end{align*}$$

• $P_A = I - A^T (A A^T)^{-1} A$：$A$的投影矩阵
• 投影矩阵$P_A$可由点对线性约束的投影定义，利用拉格朗日 求解

证明

$$\begin{align*} x_1 & = x - x_2 = x - A^T y \\ A x_1 & = A x - A A^T y \\ \Rightarrow y & = (A A^T)^{-1} A (x - x_1) \\ \Rightarrow x_1 & = x - A^T[(A A^T)^{-1} A (x - x_1)] \\ & = x - A^T (A A^T)^{-1} A x - A^T (A A^T)^{-1} A x_1 \\ & = (I - A^T (A A^T)^{-1} A) x = P_A x \end{align*}$$

• 投影矩阵$P$对值应用多次线性变换和只应用一次结果相同， 保持像不变

Projection Operator

$$\begin{array}{l} \min & f(x) \\ s.t. & A_1 x \leq b_1 \\ & A_2 x = b_2 \end{array}$$

• 设$x^{k}$为当前迭代点，记$A{11}$、$A{12}$分别为紧、松 约束，即

  $$\begin{align*} A_1 & = \begin{bmatrix} A_{1,1} \\ A_{1,2} \end{bmatrix}, & b_1 & = \begin{bmatrix} b_{1,1} \\ b_{1,2} \end{bmatrix} \\ A_{1,1} x^k & = b_{1,1}, & A_{1,2} x^k & \leq b_{1,2} \end{align*}$$

• 记$M = [A_{1,1}^T, A_2^T]^T$，则$s \in L_M$时是可行方向

• 对负梯度$\nabla f(x^k)$，通过$M$的投影矩阵$P_M$将其投影 至$L_M$上即得可行下降方向$s^k = -P_M \nabla f(x^k)$

  • $s^k \neq 0$：为$x^k$处可行下降方向
  • $s^k = 0$：作如下讨论

投影方向为0

• 记$w = [u, v]^T = -(M M^T)^{-1}M \nabla f(x^k)$，则有

  $$\begin{align*} 0 & = \nabla f(x^k) + M^T w \\ & = \nabla f(x^k) + [A_{1,1}^T, A_2^T] \begin{bmatrix} u \\ v \end{bmatrix} \\ & = \nabla f(x^k) + A_{1,1}^T u + A_2^T v \end{align*}$$

• 若$u \geq 0$，则$x^{k}$是KKT点

  $$\nabla f(x^k) + A_{1,1}^T u + A_{1,2}^T v = 0 \Rightarrow x^k 为KKT点$$

• 否则若$u$中有负分量，可设$u0 < 0$，记$\bar M$为$M$中 去除对应列矩阵，则$\bar s^k = -P{\bar M}\nabla f(x^k)$ 为$x^k$可行下降方向

  • 先反证法证明$\bar s^k \neq 0$，若$\bar s^k = 0$

    $$\begin{align*} 0 & = \nabla f(x^k) - \bar M^T (\bar M \bar M^T)^{-1} \bar M \nabla f(x^k) \\ & = \nabla f(x^k) + \bar M^T \beta \\ \beta & = -(\bar M \bar M^T)^{-1} \bar M \nabla f(x^k) \end{align*}$$

    考虑到

    $$\begin{align*} 0 & = \nabla f(x^k) + M^T w \\ & = \nabla f(x^k) + u_0 \alpha_0 + \bar M^T \bar w \end{align*}$$

    • $\alpha_0$：$M$中$u_0$对应行

    则有

    $$u_0 \alpha_0 + \bar M^T (\bar w - \beta) = 0$$

    与$M$行满秩条件矛盾，故$\bar s^k \neq 0$

  • 证明$\bar s^k$为下降方向

    $$\begin{align*} \nabla f(x^k)^T \bar s^k & = -\nabla f(x^k) P_{\bar M} \nabla f(x^k) \\ & = -\nabla f(x^k) P_{\bar M}^T P_{\bar M} \nabla f(x^k) \\ & = -\|P_{\bar M} \nabla f(x^k)\|_2^2 \leq 0 \end{align*}$$

  • 证明$\bar s^k$方向可行（满足约束）

    • 由$P{\bar M}$定义：$\bar M P{\bar M} = 0$，则

      $$\begin{align*} \bar M \bar s^k & = -\bar M \bar P_{\bar M} \nabla f(x^k) \\ & = \begin{bmatrix} \bar A_{1,1} \\ A_2 \end{bmatrix} \bar s^k = 0 \end{align*}$$

    • 则只需证明$\alpha_0^T \bar s^k < 0$

      $$\begin{align*} 0 & = \nabla f(x^k) + M^T w \\ & = \nabla f(x^k) + u_0 \alpha_0 + \bar M^T \bar w \\ \Rightarrow & = \nabla f(x^k)^T \bar s^k + u_0 \alpha_0^T \bar s^k + \bar w^T \bar M \bar s^k \\ & = \nabla f(x^k)^T \bar s^k + u_0 \alpha_0^T \bar s^k \end{align*}$$

      考虑到$u_0 < 0$，则$\alpha_0^T \bar s^k < 0$

  • 即此时有紧约束变为松约束

算法

• 初始化：初始点$x^0$、$k=0$、精度参数$\epsilon > 0$

• 构造$M = [A_{1,1}^T, A_2^T]^T$

  • 若$M=0$（在可行域内），令$s^k = -\nabla f(x^k)$为 迭代方向
  • 否则令$s^k = -P_M \nabla f(x^k)$为迭代方向

• 若$|s^k|_2^2 \geq \epsilon$

  • 若$M$为空（无可下降方向），停止
  • 若$M$非空、$u > 0$，停止
  • 否则，构建$M = \bar M$继续

• 若$|s^k|_2^2 > \epsilon$，确定步长$\lambda_k$

  • 显然只需保证$A_2 x_k + \lambda_k A_2 d_k \leq b_2$ 即可

  • 若$A_2 d_k < 0$，则$\lambda_k$无约束，否则

    $$\lambda_k = \max \{\frac {(b_2 - A_2 x_k)_i} {(A_2 d_k)_i}\}$$

  • 即单纯型法中确定步长方法

• 得到新迭代点$x^{k+1} = x^k + \lambda_k s^k$、$k=k+1$

约束问题局部解

$$\begin{array}{l} \min & f(x), x \in R^n \\ s.t. & c_i(x) = 0, i \in E = \{1,2,\cdots,l\}, \\ & c_i(x) \leq 0, i \in I = \{l,l+1,\cdots,l+m\} \end{array}$$

• 对于一般约束优化问题，记其可行域为

  $$D = \{x| c_i(x) = 0, i \in E, c_i(x) \leq 0, i \in I\}$$

• 若 $\forall x^{} \in D, \exists \epsilon$，使得当 $x \in D, |x - x^{}| \leq \epsilon$ 时，总有

  $$f(x) \geq f(x^{*})$$

  则称$x^{*}$为约束问题的局部解，简称为最优解

• 若 $x \in D, 0 < |x - x^{*}| \leq \epsilon$ 时，总有

  $$f(x) > f(x^{*})$$

  则称$x^{*}$是约束问题的严格局部最优解

约束问题局部解一阶必要条件

定理1

• 设 $a_1,a_2,\cdots,a_m$ 和 $w \in R^n$，$C$ 定义如下 $$

    C = \{v |\sum_{i=1}^m \lambda_i a_i, \lambda_i \geq 0,
    i=1,2,\cdots,m \}
  

  $$若 $w \notin C$，则存在超平面 $d^T w = 0$，分离 $C$ 和 $w$，即$$ \begin{align*}

    d^T w & \leq 0 \\
    d^T w & > 0
  

  \end{align*}$$

• 显然C是闭凸集，则$\exists d \in R^n, d \neq 0$， $\alpha \in R$，使得

  $$\begin{array}{l} d^T x \leq \alpha, & \forall x \in C \\ d^T w > \alpha & \end{array}$$

• 又C是锥，有$0 \in C$，所以$\alpha \geq 0$，即$d^T w > 0$

• 若$\exists \bar x \in C, d^T \bar x > 0$，则 $\forall \lambda \geq 0, \lambda \bar x \in C$，则有

  $$\lambda d^T \bar x \leq \alpha$$

  而$\lambda \rightarrow \infty$，左端趋于无穷，矛盾

Farkas引理

• 设$a_1,a_2,\cdots,a_m$和$w \in R^n$，则以下两个系统有且 仅有一个有解

  • 系统I：存在$d$满足 $$\begin{align*} a_i^T d & \leq 0, & i=1,2,\cdots,m \\ w^T d & > 0 \end{align*}$$
  • 系统II：存在非负常数$\lambda_1,\cdots,\lambda_m$使得 $$w =\sum_{i=1}^m \lambda_i a_i$$

• 若系统II有解，则系统I无解

  • 若系统II有解，即存在$\lambda_1,…,\lambda_m$且 $\lambda_i \geq 0,i=1,2,\cdot,m$，使得

    $$w = \sum_{i=1}^m \lambda_i a_i$$

  • 若系统I有解，则有

    $$0 < w^T d = \sum_{i=1}^m \lambda_i a_i^T d \leq 0$$

    矛盾，因此系统I无解

• 若系统II无解，则系统I有解

  • 系统II误解，构造闭凸锥

    $$C = \{v |\sum_{i=1}^m \lambda_i a_i, \lambda_i \geq 0, i=1,2,\cdots,m \}$$

    显然$w \notin C$

  • 由定理1，存在d满足

    $$\begin{array}{l} d^T x \leq 0, & \forall x \in C, \\ d^T w & > 0 \end{array}$$

• 此定理就是点要么在凸锥C内、边缘（系统II），要么在凸锥 外（系统I）

推论1

• 设$a_1,a_2,\cdots,a_m$和$w \in R^n$，则以下系统有且仅有 一个有解

  • 系统I：存在d满足 $$\begin{array}{l} a_i^T d \leq 0, & i=1,2,\cdots,m \\ d_j \geq 0, & j=1,2,\cdots,n \\ w^T d > 0 & \end{array}$$
  • 系统II：存在非负常数$\lambda_1,…,\lambda_m$使得 $$w \leq \sum_{i=1}^m \lambda_i a_i$$

• 若系统II有解，则系统I无解

  • 若系统I有解，取d带入矛盾

• 若系统II无解，则系统I有解

  • 若系统I无解

    todo

推论2

• 设$a1,a_2,\cdots,a{l+m}$和$w \in R^n$，则以下两个系统 有且进一有一个存在解

  • 存在d满足 $$\begin{array}{l} a_i^T d = 0, & i=1,2,\cdots,l \\ a_i^T d \leq 0, & i=l+1,l+2,\cdots,l+m \\ w^T d > 0 \end{array}$$
  • 存在常数$\lambda1,\lambda_2,\cdots,\lambda{l+m}$ 且$\lambda_i \geq 0, i=l+1, l+2, \cdots, l+m$使得 $$w = \sum_{i+1}^{l+m} \lambda_i a_i$$

迭代求解

参数部分更新

参数部分更新：每次更新一个或一组待估参数

• 应用场合

  • 适合待估参数较少、同时估计较慢，待估参数较多可能更新 速度慢，往往需要多次迭代更新参数
  • 一般用在机器学习算法中比较多

• 特点（某些算法）

  • 良好的并行特性：能够同时更新多个参数

    • Alternating Direction Method of Multipliers

  • 采用贪心策略的算法：可能无法得到最优解

    • 前向回归
    • 深度学习：网络层次太深，有些算法采用固化部分 网络结构，估计剩余部分

  • 能够平衡全局、局部：得到较好的解

    • LARS