Matrix Derivative/Matrix Differential
矩阵求导/矩阵微分
Layout Conventions
矩阵求导:在矩阵空间的多元微积分
- numerator layout:分子布局,微分分子的维数决定微分结果 的高维度结构(行优先,如:微分矩阵行数等于分子维数)
- denominator layout:分母布局,微分分母的维数为微分结果 的高维度结构(行优先)
- 两种布局方式相差转置
- 与微分分子、分母为行、或列向量无关 (即当微分分子、分母为向量时,行、列向量结果相同,只与 维度有关)
- 此布局模式仅讨论简单单因子微分时布局模式,复合多因子 应使用维度分析考虑 (即若严格按照计算规则,结果应该满足布局)
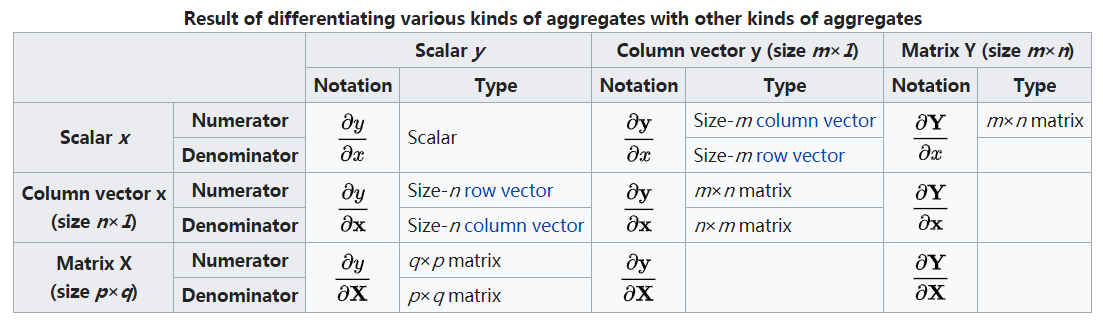
- 数分中Jaccobi行列式采用分子布局,以下默认为分子布局
维度分析
维度分析:对求导结果的维度进行分析,得到矩阵微分结果
- 维度一般化:将向量、矩阵维度置不同值,便于考虑转置
- 拆分有关因子:利用求导乘法公式(一般标量求导)拆分 因子,分别考虑各因子微分结果
- 变换微分因子、剩余因子(可能有左右两组),以满足矩阵运算
维度要求
- 微分因子:按布局模式考虑维度、不转置
- 剩余因子:为满足最终结果符合维度布局,考虑转置
- 若维度一般化也无法唯一确定剩余因子形式,再考虑行、列 內积对应关系
- 考虑到矩阵乘法定义(左乘矩阵行数为乘法结果行数),则在 分子布局(分子行优先),简单微分中若微分因子为右乘矩阵、 剩余因子为左乘矩阵,则类似标量系数在前求微分,否则 结果需转置
例
考虑$\frac {\partial x^T A x} {\partial x}$,其中 $A \in R^{n*n}, x \in R^n$
维度一般化:$\frac {\partial u^T A v} {\partial x}$, 其中$A \in R^{a * b}, x \in R^n$
拆分有关因子,变换微分、剩余因子
则有
关于标量导数
标量对标量
标量$y$对标量$x$求导:$\frac {\partial y} {\partial x}$
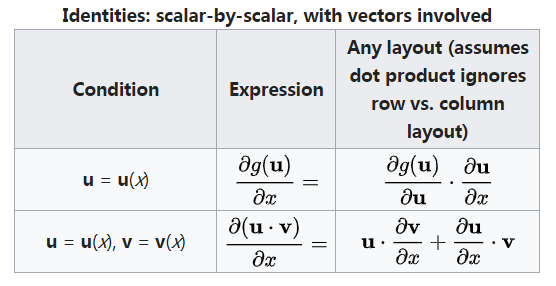

向量对标量
向量$Y$关于标量$x$求导($Y$为行、列向量均如此)
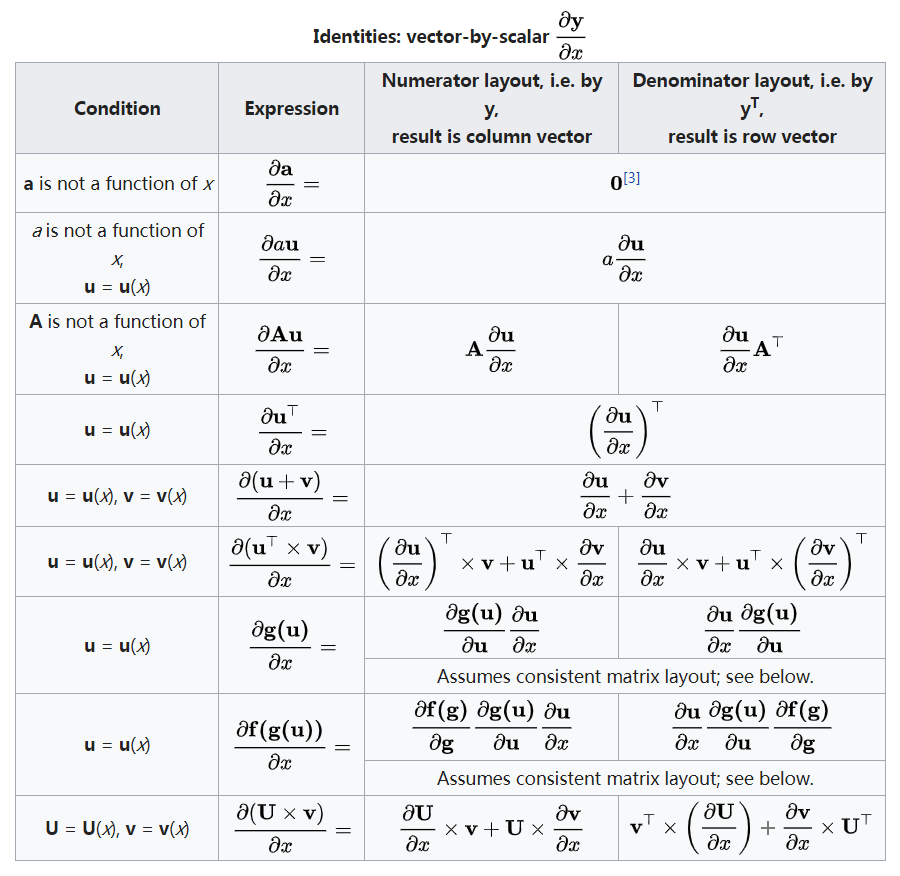
矩阵对标量
矩阵$Y$关于标量$x$求导
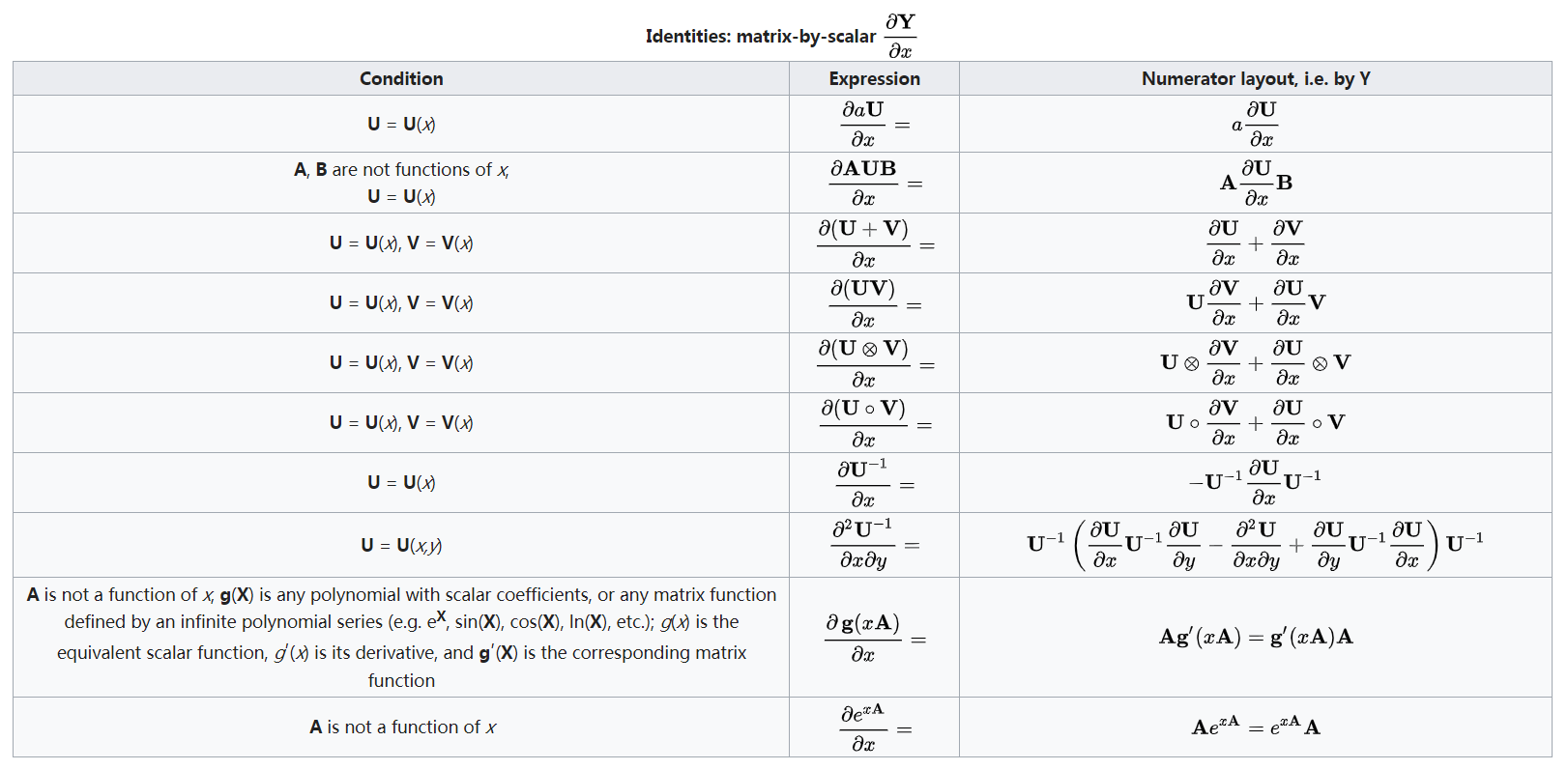
关于向量导数
标量对向量
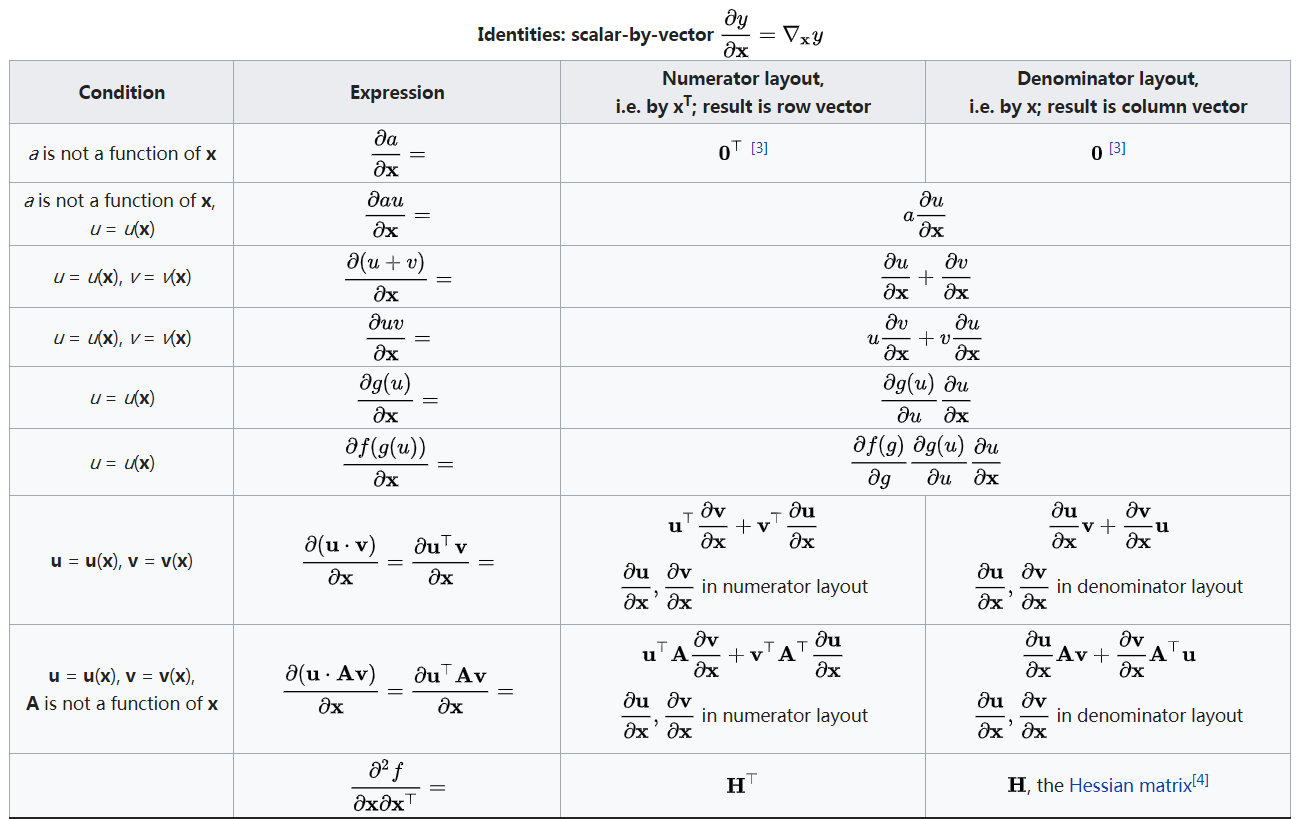
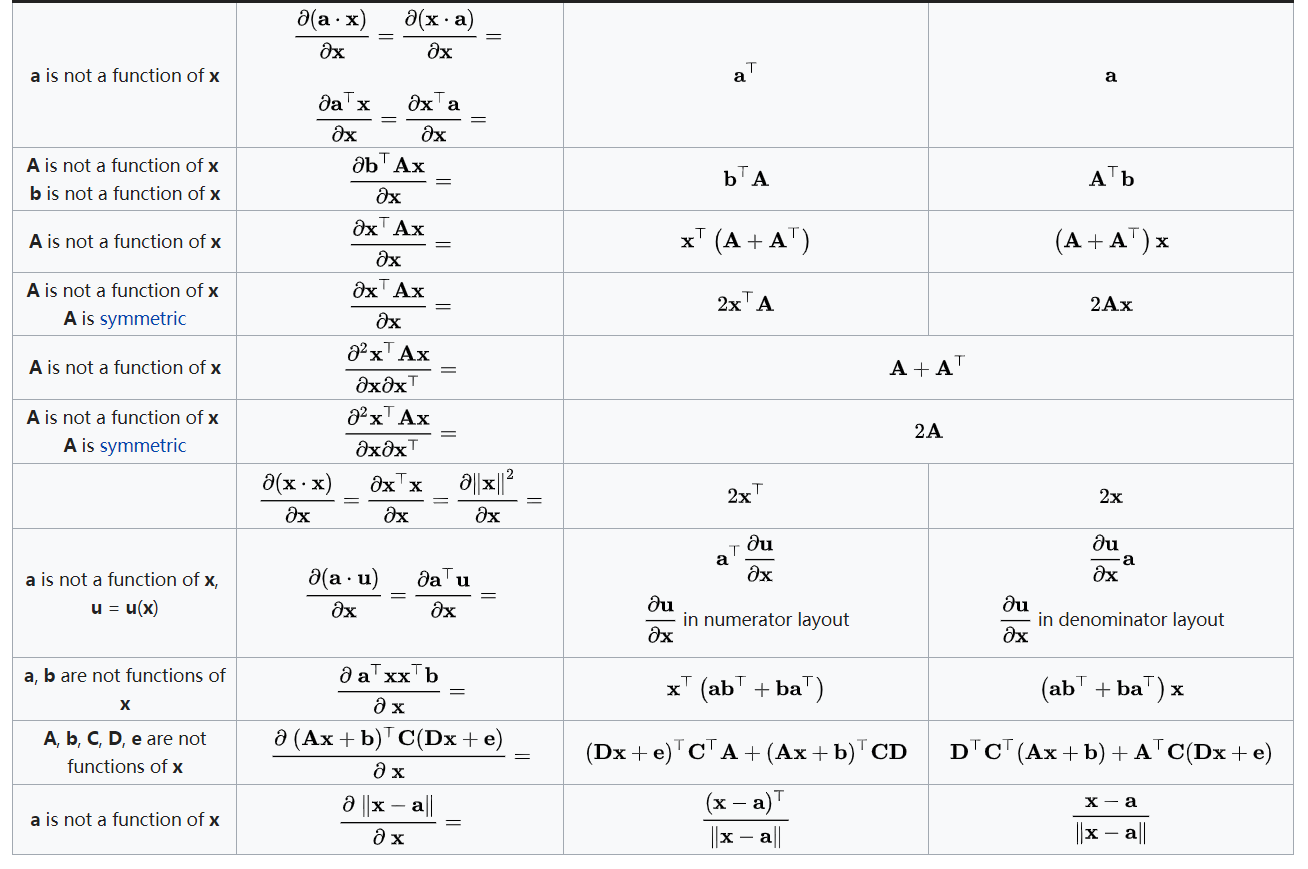
标量$y$关于向量$X$求导
向量对向量
向量$Y$关于向量$X$求导
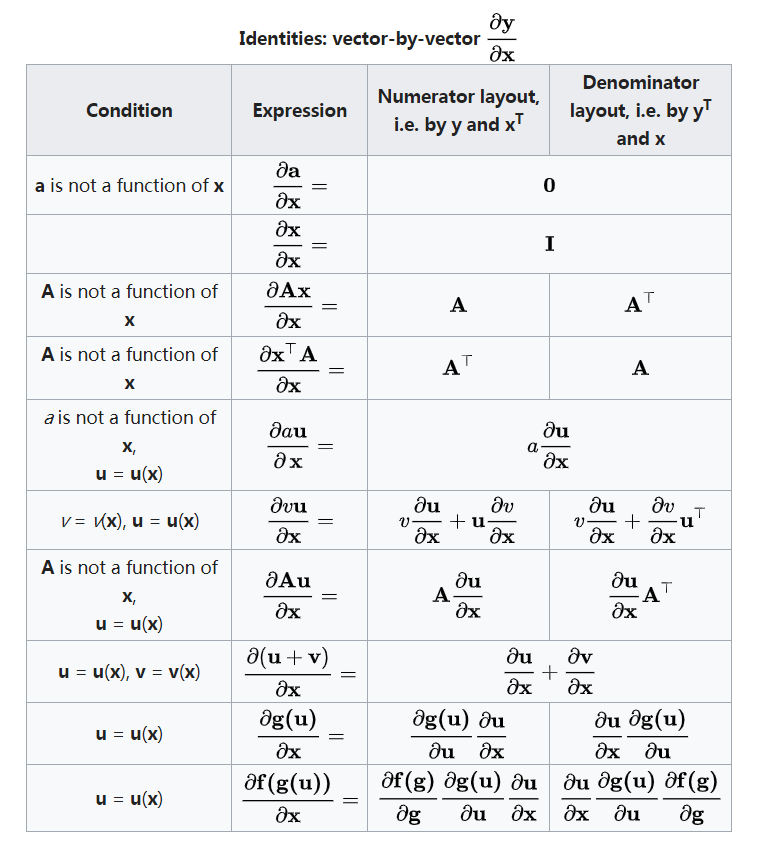
- $Y$、$X$为行、列向量均如此
关于矩阵导数
标量对矩阵求导

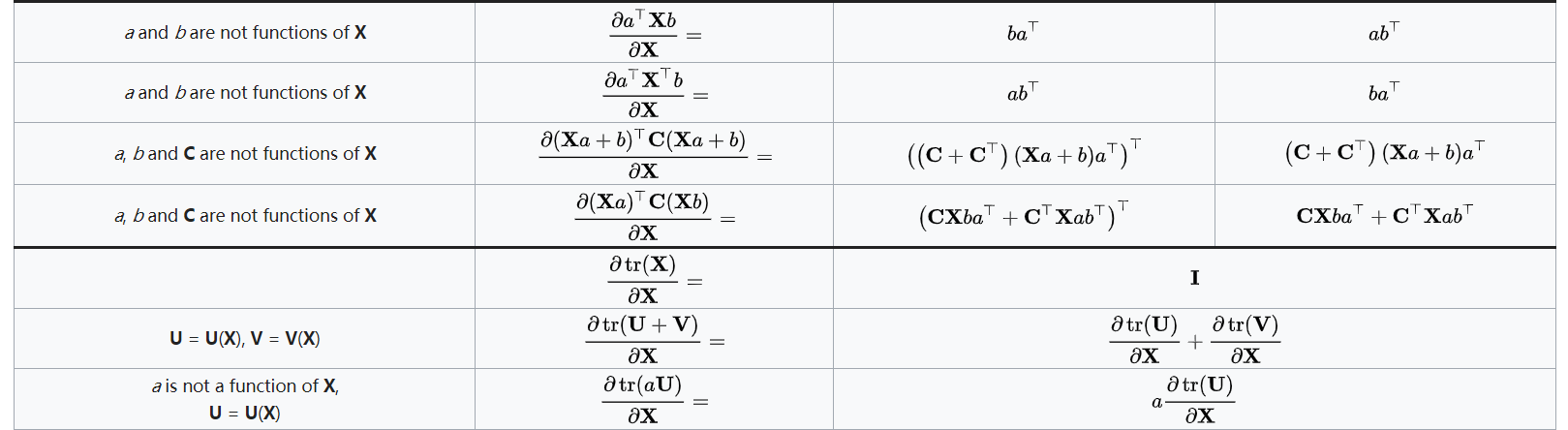
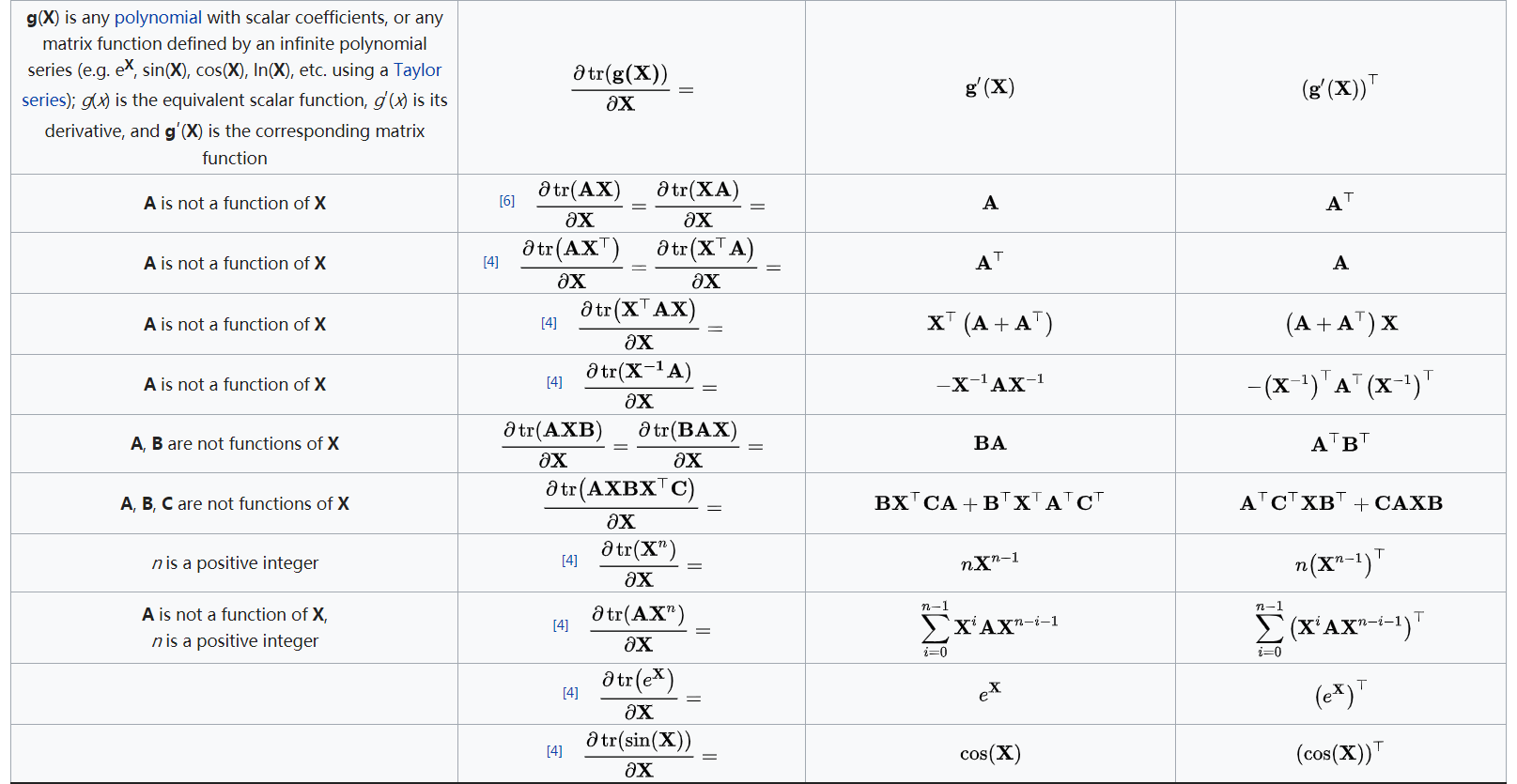
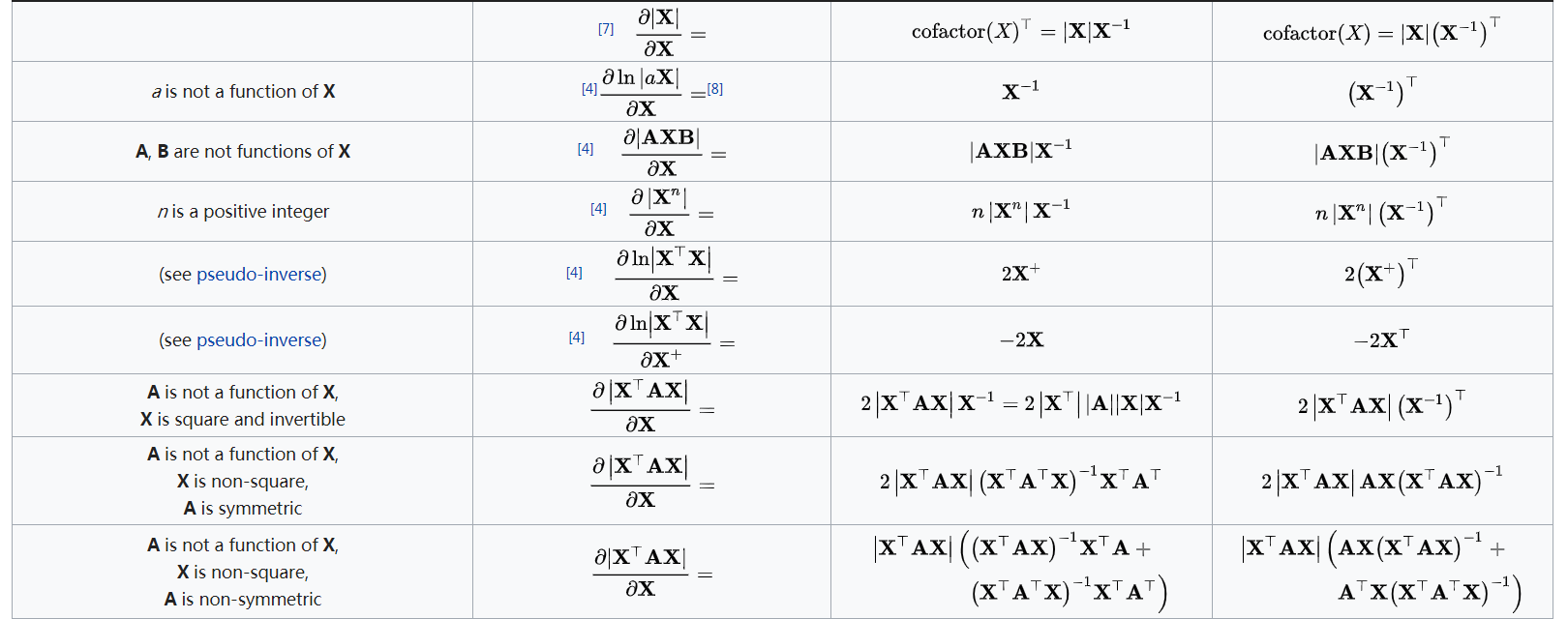
微分
微分形式
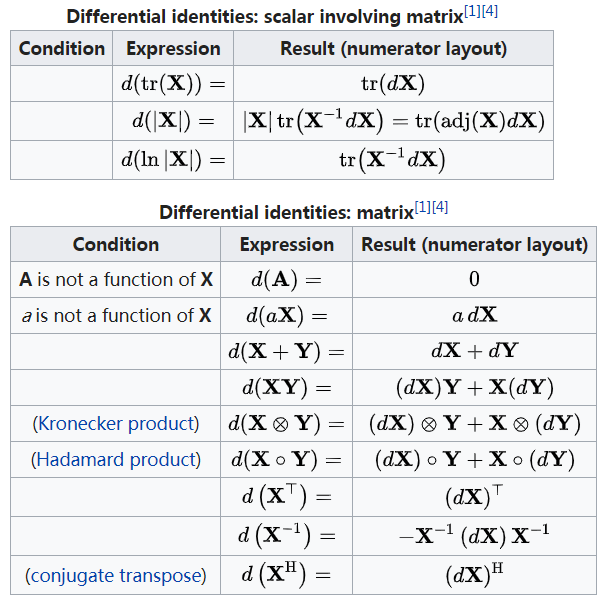
导数、微分转换
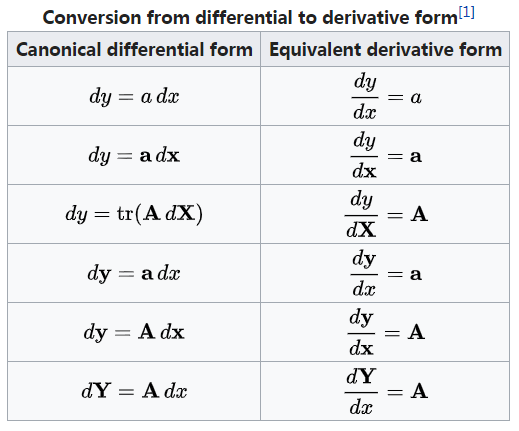
Matrix Derivative/Matrix Differential
https://xyy15926.github.io/Math-Algebra/Linear-Algebra/matrix_derivative.html

