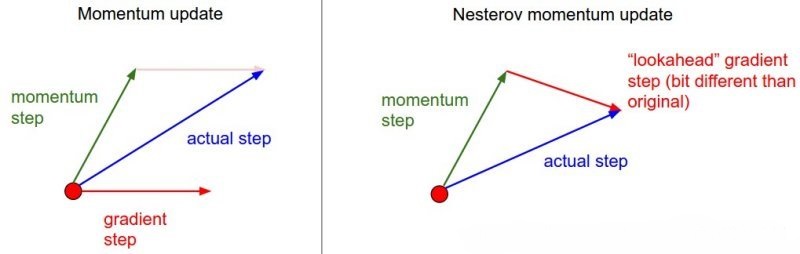
次梯度

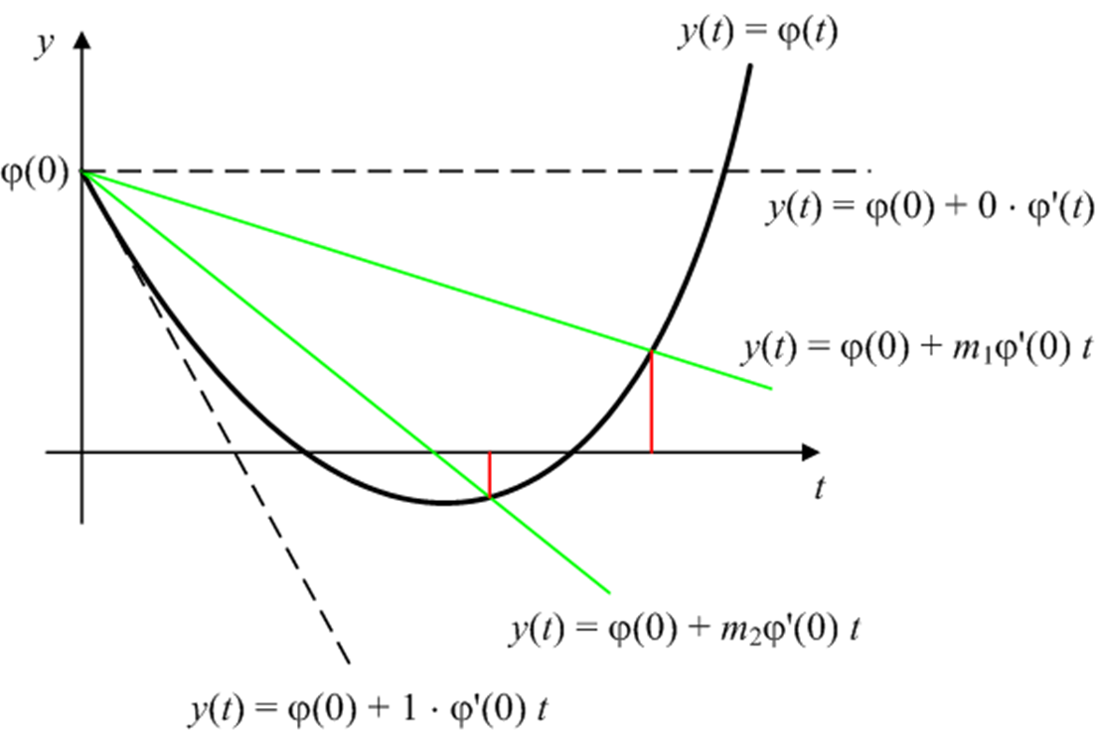
• 次梯度：实变量凸函数 $f$ 在点 $x_0$ 的次梯度 $c$ 满足

  $$\forall x, f(x) - f(x_0) \geq c(x - x_0)$$

• 可证明凸函数 $f$ 在 $x_0$ 处所有次梯度的集合 $\partial f(x)$ 是非空凸紧集

  • $\partial f(x) = [a, b]$，其中$a, b$为单侧极限

    $$\begin{align*} a & = lim_{x \rightarrow x_0^{-}} \frac {f(x) - f_0(x)} {x - x_0} \\ b & = lim_{x \rightarrow x_0^{+}} \frac {f(x) - f_0(x)} {x - x_0} \end{align*}$$

• 凸函数均指下凸函数，梯度不减

次梯度性质

运算性质

• 数乘性质

  $$\partial(\alpha f)(x) = \alpha \partial f(x), \alpha > 0$$

• 加法性质

  $$\begin{align*} f &= f_1 + f_2 + \cdots + f_m, \\ \partial f &= \partial f_1 + \cdots + \partial f_m \end{align*}$$

• 仿射性质：$f$为凸函数

  $$\begin{align*} h(x) &= f(Ax + b) \\ \partial h(x) &= A^T \partial f(Ax + b) \end{align*}$$

最优化性质

• 凸函数 $f$ 在点 $x_0$ 可导，当且仅当次梯度仅包含一个点，即该点导数

• 点 $x_0$ 是凸函数 $f$ 最小值，当且仅当次微分中包含 0 （此性质为“可导函数极小点导数为 0 ”推广）

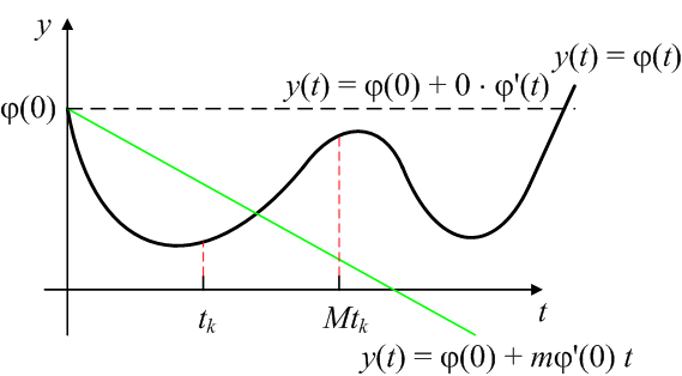
• 负次梯度方向不一定是下降方向

次梯度求解

• 逐点（分段）极值的函数求次梯度
• 求出该点相应极值函数
• 求出对应梯度即为次梯度

Pointwise Maximum

逐点最大函数：目标函数为

$$\begin{align*} f(x) & = max \{f_1(x), f_2(x), \cdots, f_m(x)\} \\ I(x) & = \{i | f_i(x) = f(x)\} \end{align*}$$

• $I(x)$：保存 $x$ 处取值最大的函数下标

• 弱结果：$I(x)$ 中随机抽取，以 $f_i(x)$ 在该处梯度作为次梯度

• 强结果

  $$\partial f(x) = conv \cup_{i \in I(x)} \partial f_i(x)$$
  • 先求支撑平面，再求所有支撑平面的凸包
  • 可导情况实际上是不可导的特殊情况

分段函数

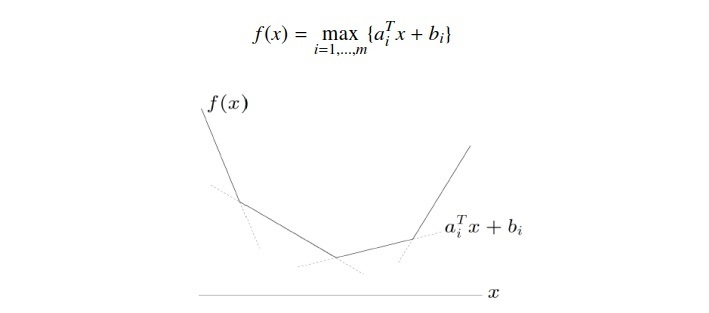
• 折点处

  $$\partial f(x) = conv\{a_i, a_{i+1}\} = [a_i, a_{i+1}]$$

• 非折点处

  $$\partial f(x) = {a_i}$$

$L_1$范数

PointWise Supremum

逐点上确界：目标函数为

$$\begin{align*} f(x) &= \sup_{\alpha \in A} f_{\alpha}(x) \\ I(x) &= \{\alpha \in A | f_{\alpha}(x) = f(x)\} \end{align*}$$

• 弱结果：可行梯度为

  $$\partial (\max_{\alpha} f_{\alpha}(x)) \in partial f(x)$$

• 强结果

  $$\partial f(x) = conv \cup_{\alpha \in I(x)} \partial f_{alpha}(x) \subseteq \partial f(x)$$

最大特征值

$$\begin{align*} f(x) & = \lambda_{max}(A(x)) = \sup_{\|y\|_2 = 1} \\ A(x) & = A_0 + x_1 A_1 + \cdots + x_n A_n \end{align*}$$

• $A_n$：对称矩阵

• 对确定 $\hat {x}$，$A(x)$ 最大特征值 $\lambda_{max}$、对应特征向量 $y$，则该点此梯度为

  $$(y^T A_0 y, \cdots, y^T A_n y)$$

Pointwise Inferior

逐点下确界：目标函数为

$$f(x) = \inf_y h(x, y)$$

• $h$：凸函数

• 弱结果：给定$x = \hat x$，可行次梯度为

  $$(\partial h(x, \hat y)|_{x=\hat x}, 0) \in \partial f(x)$$

复合函数

$$f(x) = h(f_1(x), \cdots, f_n(x))$$

• $h$：凸、不降函数
• $f_i$：凸函数

• 弱结果：给定$x = \hat x$，可行次梯度为

  $$g = z_1 g_1 + \cdots + z_k g_k \in \partial f(\hat x)$$

  • $z \in \partial h(f_1(\hat x), \cdots, f_k(\hat x))$
  • $g_i \in \partial f_i(\hat x)$

  • 证明

    $$\begin{align*} f(x) & \geq h(f_1(\hat x) + g_1^T(x - \hat x), \cdots, f_k(\hat x) + g_k^T(x - \hat x) \\ & \geq h(f_1(\hat x), \cdots, f_k(\hat x)) + z^T(g_1^T(x - \hat x), \cdots, g_k^T(x - \hat x)) \\ & = f(\hat x) + g^T(x - \hat x) \end{align*}$$

次梯度法

$$\begin{align*} x^{(k+1)} & = x^{(k)} + \alpha_k g^{(k)} \\ f_{best}^{(k+1)} & = min{f_{best}^{(k)}, f(x^{(k+1)})} \end{align*}$$

• $g^{(k)}$：函数$f$在$x^{(k)}$处次梯度

• 求解凸函数最优化的问题的一种迭代方法

• 相较于较内点法、牛顿法慢

  • 应用范围更广泛：能够用于不可微目标函数，目标函数可微时，无约束问题次梯度与梯度下降法有同样搜索方向
  • 空间复杂度更小
  • 可以和分解技术结合，得到简单分配算法
  • 通常不会产生稀疏解

步长选择

• 次梯度法选取步长方法很多，以下为保证收敛步长规则

• 恒定步长：$\alpha_k = \alpha$
• 恒定间隔：$\alpha_k = \gamma / |g^{(k)}|_2$
• 步长平方可加、步长不可加：$\sum{k=1}^{\infty} \alpha_k^2 < \infty, \sum{k=1}^{\infty} \alpha_k = \infty$
• 步长不可加、但递减：$lim_{k \rightarrow \infty} \alpha_k = 0$
• 间隔不可加、但递减：$lim_{k \rightarrow \gamma_k} \gamma_k = 0$

Hash Function

• hash：散列/哈希，将任意类型值转换为关键码值
• hash function：哈希/散列函数，从任何数据中创建小的数字“指纹”的方法
• hash value：哈希值，哈希函数产生关键码值
• collision：冲突，不同两个数据得到相同哈希值

• 哈希函数应该尽可能使得哈希值均匀分布在目标空间中
  • 降维：将高维数据映射到低维空间
  • 数据应该低维空间中尽量均匀分布

数据相关性

• Data Independent Hashing：数据无关哈希，无监督，哈希函数基于某种概率理论

  • 对原始的特征空间作均匀划分
  • 对分布不均、有趋向性的数据集时，可能会导致高密度区域哈希桶臃肿，降低索引效率

• Data Dependent Hashing：数据依赖哈希，有监督，通过学习数据集的分布从而给出较好划分的哈希函数

  • 得到针对数据密度动态划分的哈希索引
  • 破坏了传统哈希函数的数据无关性，索引不具备普适性

应用

• 查找数据结构：cs_algorithm/data_structure/hash_table
  • 哈希表
• 信息安全方向：cs_algorithm/specification/info_security
  • 文件检验
  • 数字签名
  • 鉴权协议

哈希函数

• 简单哈希函数主要用于提升查找效率（构建哈希表）

  • 要求哈希函数的降维、缩小查找空间性质
  • 计算简单、效率高

• 复杂哈希函数主要用于信息提取

  • 要求哈希函数的信息提取不可逆、非单调映射
  • 查表哈希
    • CRC 系列算法：本身不是查表，但查表是其最快实现
    • Zobrist Hashing
  • 混合哈希：利用以上各种方式
    • MD5
    • Tiger

单值输入

• 直接寻址法：取关键字、或其某个线性函数值 $hash(key) = (a * key + b) \% prime$

  • $prime$：一般为质数，以使哈希值尽量均匀分布，常用的如：$2^{32}-5$

• 数字分析法：寻找、利用数据规律构造冲突几率较小者

  • 如：生日信息前 2、3 位大体相同，冲突概率较大，优先舍去

• 平方取中法：取关键字平方后中间几位

• 折叠法：将关键字分割为位数相同部分，取其叠加和

• 随机数法：以关键字作为随机数种子生成随机值

  • 适合关键字长度不同场合

• 常用于之前哈希结果再次映射为更小范围的最终哈希值

序列输入

加法哈希

加法哈希：将输入元素相加得到哈希值

• 标准加法哈希

  1 2 3 4 5 6

  AddingHash(input): hash = 0 for ele in input: hash += ele # prime 为任意质数，常用 2^32 - 5 hash = hash % prime

  • 最终哈希结果 $\in [0, prime-1]$

位运算哈希

位运算哈希：利用位运算（移位、异或等）充分混合输入元素

• 标准旋转哈希

  1 2 3 4 5

  RotationHash(input): hash = 0 for ele in input: hash = (hash << 4) ^ (hash >> 28) ^ ele return hash % prime

• 变形 1

  1	hash = (hash<< 5) ^ (hash >> 27) ^ ele

• 变形2

  1 2 3

  hash += ele hash ^= (hash << 10) hash ^= (hash >> 6)

• 变形3

  1 2 3 4

  if (ele & 1) == 0: hash ^= (hash << 7) ^ ele ^ (hash >> 3) else: hash ^= ~((hash << 11) ^ ele ^ (hash >> 5))

• 变形4

  1	hash += (hash << 5) + ele

• 变形5

  1	hash = ele + (hash << 6) + (hash >> 16) - hash

• 变形6

  1	hash ^= (hash << 5) + ele + (hash >> 2)

乘法哈希

乘法哈希：利用乘法的不相关性

• 平方取头尾随机数生成法：效果不好

• Bernstein 算法

  1 2 3 4 5

  Bernstein(input): hash = 0 for ele in input: hash = 33 * hash + ele return hash

  • 其他常用乘数：31、131、1313、13131、131313

• 32位 FNV 算法

  1 2 3 4 5 6 7

  M_SHIFT = M_MASK = FNVHash(input): hash = 2166136261; for ele in input: hash = (hash * 16777619) ^ ele return (hash ^ (hash >> M_SHIFT)) & M_MASK

• 改进的 FNV 算法

  1 2 3 4 5 6 7 8 9 10

  FNVHash_2(input): hash = 2166136261; for ele in input: hash = (hash ^ ele) * 16777619 hash += hash << 13 hash ^= hash >> 7 hash += hash << 3 hash ^= hash >> 17 hash += hash << 5 return hash

• 乘数不固定

  1 2 3 4 5 6 7

  RSHash(input): hash = 0 a, b = 378551, 63689 for ele in input: hash = hash * a + ele a *= b return hash & 0x7FFFFFFF

• 除法也类似乘法具有不相关性，但太慢

定长序列

• 两步随机数

  1 2 3 4 5 6

  main_rand_seq = randint(k) TwoHashing(input[0,...,k]): hash = 0 from i=0 to k: hash += input[i] * main_rand_seq[i] hash = hash mod prime

Universal Hashing

• 全域哈希：键集合 $U$ 包含 $n$ 个键、哈希函数族 $H$ 中哈希函数 $h_i: U \rightarrow 0..m$，若 $H$ 满足以下则为全域哈希 $$

    \forall x \neq y \in U, | \{h|h \in H, h(x) = h(y) \} | = \frac {|H|} m
  

  $$

  • $|H|$：哈希函数集合 $H$ 中函数数量

• 独立与键值随机从中选择哈希函数，避免发生最差情况
• 可利用全域哈希构建完美哈希

性质

• 全域哈希 $H$ 中任选哈希函数 $h_i$，对任意键 $x \neq y \in U$ 冲突概率小于 $\frac 1 m$

  • 由全域哈希函数定义，显然

• 全域哈希 $H$ 中任选哈希函数 $hi$，对任意键 $x \in U$，与其冲突键数目期望为 $\frac n m$，即 $E{[collision_x]}=\frac n m$

  $$\begin{align*} E(C_x) &= E[\sum_{y \in U - \{x\}} C_{xy}] \\ &= \sum_{y \in U - \{x\}} E[C_{xy}] \\ &= \sum_{y \in U - \{x\}} \frac 1 m \\ &= \frac {n-1} m \end{align*}$$

  • $C_x$：任选哈希函数，与 $x$ 冲突的键数量
  • $C_{xy} = \left { \begin{matrix} 1, & h_i(x) = h_i(y) \ 0, & otherwise \end{matrix} \right.$：指示 $x,y$ 是否冲突的指示变量

  • $m = n^2$ 时，冲突期望小于 0.5
    • $n$ 个键两两组合数目为 $C_n^2$
    • 则 $E_{total} < C_n^2 \frac 1 n < 0.5$

例

• 以下构造 $[0,p-1] \rightarrow [0,m-1]$ 全域哈希

• $p$ 为足够大素数使得所有键值 $\in [0,p-1]$

  • 记 $Z_p = { 0,1,\cdots,p-1 }$
  • 记 $Z_p^{*}={ 1,2,\cdots,p-1 }$
  • 且哈希函数映射上限（哈希表长度） $m < max(U) < p$

• 记哈希函数

  $$\forall a \in Z_p^{*}, b \in Z_p, h_{a, b}(k) = ((a k + b) \% p) \% m$$

• 则以下哈希函数族即为全域哈希

  $$H_{p,m} = {h_{a,b}|a \in Z_p^{*}, b \in Z_p}$$

Locality Sensitive Hashing

LSH：局部敏感哈希

• $(r_1,r_2,P_1,P_2)-sensitive$ 哈希函数族 $H$ 需满足如下条件 $$ \begin{align*}

    Pr_{H}[h(v) = h(q)] \geq P_1, & \forall q \in B(v, r_1) \\
    Pr_{H}[h(v) = h(q)] \geq P_2, & \forall q \notin B(v, r_2) \\
  

  \end{align*}$$

  • $h \in H$
  • $r_1 < r_2, P_1 > P_2$：函数族有效的条件
  • $B(v, r)$：点 $v$ 的 $r$ 邻域
  • $r_1, r_2$：距离，强调比例时会表示为 $r_1 = R, r_2 = cR$

• 此时 相似目标（距离小）有更大概率发生冲突

LSH查找

思想

• 相似目标更有可能映射到相同哈希桶中

  • 则只需要在目标所属的哈希桶中进行比较、查找即可
  • 无需和全集数据比较，大大缩小查找空间

• 可视为降维查找方法

  • 将高维空间数据映射到 1 维空间，寻找可能近邻的数据点
  • 缩小范围后再进行精确比较

概率放大

• 期望放大局部敏感哈希函数族 $Pr_1, Pr_2$ 之间差距

• 增加哈希值长度（级联哈希函数中基本哈希函数数量） $k$

  • 每个哈希函数独立选择，则对每个级联哈希函数 $g_i$ 有 $Pr[g_i(v) = g_i(q)] \geq P_1^k$
  • 虽然增加哈希键位长会减小目标和近邻碰撞的概率，但同时也更大程度上减少了和非近邻碰撞的概率、减少搜索空间

  • 级联哈希函数返回向量，需要对其再做哈希映射为标量，方便查找

• 增加级联哈希函数数量（哈希表数量） $L$

  • $L$个哈希表中候选项包含真实近邻概率 至少 为 $1 - (1 - P_1^k)^L$
  • 增加哈希表数量能有效增加候选集包含近邻可能性
  • 但同时也会增大搜索空间

搜索近似最近邻

• 使用 $L$ 个级联哈希函数分别处理待搜索目标
• 在 $L$ 个哈希表分别寻找落入相同哈希桶个体作为候选项
• 在所有候选项中线性搜索近邻

基于汉明距离的 LSH

• 在汉明距离空间中搜索近邻
  • 要求数据为二进制表示
  • 其他距离需要嵌入汉明距离空间才能使用
    • 欧几里得距离没有直接嵌入汉明空间的方法
      • 一般假设欧几里得距离和曼哈顿距离差别不大
      • 直接使用对曼哈顿距离保距嵌入方式

设计哈希函数族

• 考虑哈希函数族 $H = { h_1, h_2, \cdots, h_m }$

  • 其中函数 $h_i$ 为 ${0, 1}^d$ 到 ${0, 1}$ 的映射：随机返回特定比特位上的值

• 从 $H$ 中随机的选择哈希函数 $h_i$

  • 则 $Pr[h_i(v) = h_i(q)]$ 等于 $v, q$ 相同比特数比例，则
    • $Pr_1 = 1 - \frac R d$
    • $Pr_2 = 1 - \frac {cR} d$
  • 考虑到 $Pr_1 > Pr_2$，即此哈希函数族是局部敏感的

基于 Jaccard 系数的 LSH

• 考虑 $M * N$ 矩阵 $A$，元素为 0、1

  • 其中
    • $M$：集合元素数量
    • $N$：需要比较的集合数量
  • 目标：寻找相似集合，即矩阵中相似列

• 用 Jaccard 系数代表集合间相似距离，用于搜索近邻

  • 要求各数据向量元素仅包含 0、1：表示集合是否包含该元素

定义 Min-hashing 函数族

• 对矩阵 $A$ 进行 行随机重排 $\pi$，定义 Min-hashing 如下

  $$h_{\pi}(C) = \min \pi(C)$$

  • $C$：列，表示带比较集合
  • $\min \pi(C)$：$\pi$ 重排矩阵中 $C$ 列中首个 1 所在行数

• 则不同列（集合） Min-hashing 相等概率等于二者 Jaccard 系数

  $$\begin{align*} Pr(h_{\pi}(C_1) = h_{\pi}(C_2)) & = \frac a {a + b} \\ & = Jaccard_d(C_1, C_2) \end{align*}$$

  • $a$：列 $C_1, C_2$ 取值均为 1 的行数
  • $b$：列 $C_1, C_2$ 中仅有一者取值为 1 的行数
  • 根据 Min-hashing 定义，不同列均取 0 行被忽略

Min-hashing 实现

• 数据量过大时，对行随机重排仍然非常耗时，考虑使用哈希函数模拟行随机重排

  • 每个哈希函数对应一次随机重排
    • 哈希函数视为线性变换
    • 然后用哈希函数结果对总行数取模
  • 原行号经过哈希函数映射即为新行号

• 为减少遍历数据次数，考虑使用迭代方法求解

  1 2 3 4 5 6

  for i from 0 to N-1: for j from 0 to M-1: if D[i][j] == 1: for k from 1 to K: # 更新随机重拍后，第 `j` 列首个 1 位置 DD[k][j] = min(h_k(i), DD[k][j])

  • $D$：原始数据特征矩阵
  • $DD$：$Min-hashing* 签名矩阵
  • $N$：特征数量，原始特征矩阵行数
  • $M$：集合数量，原始特征矩阵列数
  • $K$：模拟的随机重排次数，Min-hashing 签名矩阵行数
  • $h_k,k=1,…,K$：$K$ 个模拟随机重排的哈希函数，如 $h(x) = (2x + 7) mod N$

  • 初始化 Min-hashing 签名矩阵所有值为 $\infty$
  • 遍历 $N$ 个特征、$M$ 个集合
    • 查看每个对应元素是否为 1
    • 若元素为 1，则分别使用 $K$ 个哈希函数计算模拟重排后对应的行数
    • 若计算出行数小于当前 *Min-hash$ 签名矩阵相应哈希函数、集合对应行数，更新
  • 遍历一遍原始数据之后即得到所有模拟重排的签名矩阵

Exact Euclidean LSH

• $E^2LSH$：欧式局部LSH，LSH Based-on P-stable Distribution

  • 使用内积将向量随机映射到哈希值
  • p-stable 分布性质将欧式距离同哈希值相联系，实现局部敏感

• $E^2LSH$ 特点

  • 基于概率模型生成索引编码结果不稳定
  • 随编码位数 $k$ 增加的，准确率提升缓慢
  • 级联哈希函数数量 $L$ 较多时，需要大量存储空间，不适合大规模数据索引

p-stable 哈希函数族

$$h_{a, b}(v) = \lfloor \frac {av + b} r \rfloor$$

• $v$：$n$ 维特征向量
• $a = (X_1,X_2,\cdots,X_n)$：其中分量为独立同 p-stable 分布的随机变量
• $b \in [0, r]$：均匀分布随机变量

p-stable 哈希函数碰撞概率

• 考虑$|v_1 - v_2|_p = c$的两个样本碰撞概率

• 显然，仅在 $|av1 - av_2| \leq r$ 时，才存在合适的 $b$ 使得 $h{a,b}(v1) = h{a,b}(v_2)$

  • 即两个样本碰撞，不失一般性可设 $av_1 \leq av_2$
  • 此 $r$ 即代表局部敏感的 局部范围

• 若 $(k-1)r \leq av_1 \leq av_2 < kr$，即两个样本与 $a$ 内积在同一分段内

  • 易得满足条件的 $b \in [0,kr-av_2) \cup [kr-av_1, r]$
  • 即随机变量 $b$ 取值合适的概率为 $1 - \frac {av_2 - av_1} r$

• 若 $(k-1)r \leq av_1 \leq kr \leq av_2$，即两个样本 $a$ 在相邻分段内

  • 易得满足条件的 $b \in [kr-av_1, (k+1)r-av_2)$
  • 即随机变量 $b$ 取值合适的概率同样为 $1 - \frac {av_2 - av_1} r$

• 考虑 $av_2 - av_1$ 分布为 $cX$，则两样本碰撞概率为

  $$\begin{align*} p(c) & = Pr_{a,b}(h_{a,b}(v_1) = h_{a,b}(v_2)) \\ & = \int_0^r \frac 1 c f_p(\frac t c)(1 - \frac t r)dt \end{align*}$$

  • $c = |v_1 - v_2|_p$：特征向量之间$L_p$范数距离
  • $t = a(v_1 - v_2)$
  • $f$：p稳定分布的概率密度函数

  • $p=1$ 柯西分布

    $$p(c) = 2 \frac {tan^{-1}(r/c)} \pi - \frac 1 {\pi(r/c)} ln(1 + (r/c)^2)$$

  • $p=2$ 正态分布

    $$p(c) = 1 - 2norm(-r/c) - \frac 2 {\sqrt{2\pi} r/c} (1 - e^{-(r^2/2c^2)})$$

性质、实现

限制近邻碰撞概率

• $r$ 最优值取决于数据集、查询点

  • 根据文献，建议$r = 4$

• 若要求近邻 $v \in B(q,R)$以不小于$1-\sigma$ 概率碰撞，则有

  $$\begin{align*} 1 - (1 - p(R)^k)^L & \geq 1 - \sigma \\ \Rightarrow L & \geq \frac {log \sigma} {log(1 - p(R)^k)} \end{align*}$$

  则可取

  $$L = \lceil \frac {log \sigma} {log(1-p(R)^k)} \rceil$$

• $k$ 最优值是使得 $T_g + T_c$ 最小者

  • $T_g = O(dkL)$：建表时间复杂度
  • $T_c = O(d |collisions|)$：精确搜索时间复杂度
  • $T_g$、$T_c$ 随着 $k$ 增大而增大、减小

• 具体实现参考https://www.mit.edu/~andoni/LSH/manual.pdf

限制搜索空间

• 哈希表数量 $L$ 较多时，所有碰撞样本数量可能非常大，考虑只选择 $3L$ 个样本点

• 此时每个哈希键位长 $k$、哈希表数量 $L$ 保证以下条件，则算法正确

  • 若存在 $v^{ }$ 距离待检索点 $q$ 距离小于 $r_1$，则存在 $g_j(v^{ }) = g_j(q)$

  • 与 $q$ 距离大于 $r_2$、可能和 $q$ 碰撞的点的数量小于 $3L$

    $$\sum_{j=1}^L |(P-B(q,r_2)) \cap g_j^{-1}(g_j(q))| < 3L$$

• 可以证明，$k, L$ 取以下值时，以上两个条件以常数概率成立 （此性质是局部敏感函数性质，不要求是 $E^2LSH$）

  $$\begin{align*} k & = log_{1/p_2} n\\ L & = n^{\rho} \\ \rho & = \frac {ln 1/p_1} {ln 1/p_2} \end{align*}$$

• $\rho$ 对算法效率起决定性作用，且有以下定理

  • 距离尺度 $D$ 下，若 $H$ 为 $(R,cR,p1,p_2)$-敏感哈希函数族，则存在适合 (R,c)-NN 的算法，其空间复杂度为 $O(dn + n^{1+\rho})$、查询时间为 $O(n^{\rho})$ 倍距离计算、哈希函数计算为 $O(n^{\rho} log{1/p_2}n)$， 其中 $\rho = \frac {ln 1/p_1} {ln 1/p_2}$

  • $r$ 足够大、充分远离 0 时，$\rho$ 对其不是很敏感
  • $p1, p_2$ 随 $r$ 增大而增大，而 $k = log{1/p_2} n$ 也随之增大，所以 $r$ 不能取过大值

Scalable LSH

Scalable LSH：可扩展的 LSH

• 对动态变化的数据集，固定哈希编码的局部敏感哈希方法对数据 动态支持性有限，无法很好的适应数据集动态变化

  • 受限于初始数据集分布特性，无法持续保证有效性
  • 虽然在原理上支持数据集动态变化，但若数据集大小发生较大变化，则其相应哈希参数（如哈希编码长度）等需要随之调整，需要从新索引整个数据库

• 在 $E^2LSH$ 基础上通过 动态增强哈希键长，增强哈希函数区分能力，实现可扩展 LSH

Kernel Function

• 对输入空间 $X$ （欧式空间 $R^n$ 的子集或离散集合）、特征空间 $H$ ，若存在从映射 $$

    \phi(x): X \rightarrow H
  

  $$使得对所有 $x, z \in X$ ，函数 $K(x,z)$ 满足$$

    K(x,z) = \phi(x) \phi(z)
  

  $$ 则称 $K(x,z)$ 为核函数、 $\phi(x)$ 为映射函数，其中 $\phi(x) \phi(z)$ 表示内积

• 特征空间 $H$ 一般为无穷维
  • 特征空间必须为希尔伯特空间（内积完备空间）

映射函数 $\phi$

• 映射函数 $\phi$：输入空间 $R^n$ 到特征空间的映射 $H$ 的映射

• 对于给定的核 $K(x,z)$ ，映射函数取法不唯一，映射目标的特征空间可以不同，同一特征空间也可以取不同映射，如：

  • 对核函数 $K(x, y) = (x y)^2$ ，输入空间为 $R^2$ ，有

    $$\begin{align*} (xy)^2 & = (x_1y_1 + x_2y_2)^2 \\ & = (x_1y_1)^2 + 2x_1y_1x_2y_2 + (x_2y_2)^2 \end{align*}$$

  • 若特征空间为$R^3$，取映射

    $$\phi(x) = (x_1^2, \sqrt 2 x_1x_2, x_2^2)^T$$

    或取映射

    $$\phi(x) = \frac 1 {\sqrt 2} (x_1^2 - x_2^2, 2x_1x_2, x_1^2 + x_2^2)^T$$

  • 若特征空间为$R^4$，取映射

    $$\phi(x) = (x_1^2, x_1x_2, x_1x_2, x_2^2)^T$$

核函数 $K(x,z)$

• Kernel Trick 核技巧：利用核函数简化映射函数 $\phi(x)$ 映射、内积的计算技巧

  • 避免实际计算映射函数
  • 避免高维向量空间向量的存储

• 核函数即在核技巧中应用的函数

  • 实务中往往寻找到的合适的核函数即可，不关心对应的映射函数
  • 单个核函数可以对应多个映射、特征空间

• 核技巧常被用于分类器中

  • 根据 Cover’s 定理，核技巧可用于非线性分类问题，如在 SVM 中常用
  • 核函数的作用范围：梯度变化较大的区域
    • 梯度变化小的区域，核函数值变化不大，所以没有区分能力

• Cover’s 定理可以简单表述为：非线性分类问题映射到高维空间后更有可能线性可分

正定核函数

• 设 $X \subset R^n$，$K(x,z)$ 是定义在 $X X$的对称函数，若 $\forall x_i \in \mathcal{X}, i=1,2,…,m$，$K(x,z)$ 对应的 Gram* 矩阵 $$

    G = [K(x_i, x_j)]_{m*m}
  

  $$ 是半正定矩阵，则称 $K(x,z)$ 为正定核

• 可用于指导构造核函数
  • 检验具体函数是否为正定核函数不容易
  • 正定核具有优秀性质
    • SVM 中正定核能保证优化问题为凸二次规划，即二次规划中矩阵 $G$ 为正定矩阵

欧式空间核函数

Linear Kernel

线性核：最简单的核函数

$$k(x, y) = x^T y$$

• 特点
  • 适用线性核的核算法通常同普通算法结果相同
    • KPCA 使用线性核等同于普通 PCA

Polynomial Kernel

多项式核：non-stational kernel

$$K(x, y) = (\alpha x^T y + c)^p$$

• 特点

  • 适合正交归一化后的数据
  • 参数较多，稳定

    todo

• 应用场合

  • SVM：p 次多项式分类器

    $$f(x) = sgn(\sum_{i=1}^{N_s} \alpha_i^{*} y_i (x_i x + 1)^p + b^{*})$$

Gaussian Kernel

高斯核：radial basis kernel，经典的稳健径向基核

$$K(x, y) = exp(-\frac {\|x - y\|^2} {2\sigma^2})$$

• $\sigma$：带通，取值关于核函数效果，影响高斯分布形状

  • 高估：分布过于集中，靠近边缘非常平缓，表现类似像线性一样，非线性能力失效
  • 低估：分布过于平缓，失去正则化能力，决策边界对噪声高度敏感

• 特点

  • 对数据中噪声有较好的抗干扰能力

• 对应映射：省略分母

  $$\begin{align*} K(x, y) & = exp(-(x - y)^2) \\ & = exp(-(x^2 - 2 x y - y^2)) \\ & = exp(-x^2) exp(-y^2) exp(2xy) \\ & = exp(-x^2) exp(-y^2) \sum_{i=0}^\infty \frac {(2xy)^i} {i!} \\ & = \phi(x) \phi(y) \\ \phi(x) & = exp(-x^2)\sum_{i=0}^\infty \sqrt {\frac {2^i} {i!}} x^i \end{align*}$$

  即高斯核能够把数据映射至无穷维

• 应用场合

  • SVM：高斯radial basis function分类器

    $$f(x) = sgn(\sum_{i=1}^{N_s} \alpha_i^{*} y_i exp(-\frac {\|x - y\|^2} {2\sigma^2}) + b^{*})$$

Exponential Kernel

指数核：高斯核变种，仅去掉范数的平方，也是径向基核

$$K(x, y) = exp(-\frac {\|x - y\|} {2\sigma^2})$$

• 降低了对参数的依赖性
• 适用范围相对狭窄

Laplacian Kernel

拉普拉斯核：完全等同于的指数核，只是对参数$\sigma$改变敏感 性稍低，也是径向基核

$$K(x, y) = exp(-\frac {\|x - y\|} {\sigma^2})$$

ANOVA Kernel

方差核：径向基核

$$k(x,y) = \sum_{k=1}^n exp(-\sigma(x^k - y^k)^2)^d$$

• 在多维回归问题中效果很好

Hyperbolic Tangent/Sigmoid/Multilayer Perceptron Kernel

Sigmoid核：来自神经网络领域，被用作人工神经元的激活函数

$$k(x, y) = tanh(\alpha x^T y + c)$$

• 条件正定，但是实际应用中效果不错

• 参数

  • $\alpha$：通常设置为$1/N$，N是数据维度

• 使用Sigmoid核的SVM等同于两层感知机神经网络

Ration Quadratic Kernel

二次有理核：替代高斯核，计算耗时较小

$$k(x, y) = 1 - \frac {\|x - y\|^2} {\|x - y\|^2 + c}$$

Multiquadric Kernel

多元二次核：适用范围同二次有理核，是非正定核

$$k(x, y) = \sqrt {\|x - y\|^2 + c^2}$$

Inverse Multiquadric Kernel

逆多元二次核：和高斯核一样，产生满秩核矩阵，产生无穷维的 特征空间

$$k(x, y) = \frac 1 {\sqrt {\|x - y\|^2 + c^2}}$$

Circular Kernel

环形核：从统计角度考虑的核，各向同性稳定核，在$R^2$上正定

$$k(x, y) = \frac 2 \pi arccos(-\frac {\|x - y\|} \sigma) - \frac 2 \pi \frac {\|x - y\|} \sigma \sqrt{1- \frac {\|x - y\|^2} \sigma}$$

Spherical Kernel

类似环形核，在$R^3$上正定

$$k(x, y) = 1 - \frac 3 2 \frac {\|x - y\|} \sigma + \frac 1 2 (\frac {\|x - y\|} \sigma)^3$$

Wave Kernel

波动核

$$k(x, y) = \frac \theta {\|x - y\|} sin(\frac {\|x - y\|} \theta)$$

• 适用于语音处理场景

Triangular/Power Kernel

三角核/幂核：量纲不变核，条件正定

$$k(x, y) = - \|x - y\|^d$$

Log Kernel

对数核：在图像分隔上经常被使用，条件正定

$$k(x, y) = -log(1 + \|x - y\|^d)$$

Spline Kernel

样条核：以分段三次多项式形式给出

$$k(x, y) = 1 + x^t y + x^t y min(x, y) - \frac {x + y} 2 min(x, y)^2 + \frac 1 3 min(x, y)^2$$

B-Spline Kernel

B-样条核：径向基核，通过递归形式给出

$$\begin{align*} k(x, y) & = \prod_{p=1}^d B_{2n+1}(x_p - y_p) \\ B_n(x) & = B_{n-1} \otimes B_0 \\ & = \frac 1 {n!} \sum_{k=0}^{n+1} \binom {n+1} {r} (-1)^k (x + \frac {n+1} 2 - k)_{+}^n \end{align*}$$

• $x_{+}^d$：截断幂函数 $$x_{+}^d = \left \{ \begin{array}{l} x^d, & if x > 0 \\ 0, & otherwise \\ \end{array} \right.$$

Bessel Kernel

Bessel核：在theory of function spaces of fractional smoothness 中非常有名

$$k(x, y) = \frac {J_{v+1}(\sigma\|x - y\|)} {\|x - y\|^{-n(v + 1)}}$$

• $J$：第一类Bessel函数

Cauchy Kernel

柯西核：源自柯西分布，是长尾核，定义域广泛，可以用于原始维度 很高的数据

$$k(x, y) = \frac 1 {1 + \frac {\|x - y\|^2} {\sigma}}$$

Chi-Square Kernel

卡方核：源自卡方分布

$$\begin{align*} k(x, y) & = 1 - \sum_{i=1}^d \frac {(x_i - y_i)^2} {\frac 1 2 (x_i + y_i)} \\ & \frac {x^t y} {\|x + y\|} \end{align*}$$

Histogram Intersection/Min Kernel

直方图交叉核：在图像分类中经常用到，适用于图像的直方图特征

$$k(x, y) = \sum_{i=1}^d min(x_i, y_i)$$

Generalized Histogram Intersection

广义直方图交叉核：直方图交叉核的扩展，可以应用于更多领域

$$k(x, y) = \sum_{i=1}^m min(|x_i|^\alpha, |y_i|^\beta)$$

Bayesian Kernel

贝叶斯核：取决于建模的问题

$$\begin{align*} k(x, y) & = \prod_{i=1}^d k_i (x_i, y_i) \\ k_i(a, b) & = \sum_{c \in \{0, 1\}} P(Y=c | X_i = a) P(Y=c | x_k = b) \end{align*}$$

Wavelet Kernel

波核：源自波理论

$$k(x, y) = \prod_{i=1}^d h(\frac {x_i - c} a) h(\frac {y_i - c} a)$$

• 参数

  • $c$：波的膨胀速率
  • $a$：波的转化速率
  • $h$：母波函数，可能的一个函数为 $$h(x) = cos(1.75 x) exp(-\frac {x^2} 2)$$

• 转化不变版本如下

  $$k(x, y) = \prod_{i=1}^d h(\frac {x_i - y_i} a)$$

离散数据核函数

String Kernel

字符串核函数：定义在字符串集合（离散数据集合）上的核函数

$$\begin{align*} k_n(s, t) & = \sum_{u \in \sum^n} [\phi_n(s)]_u [\phi_n(t)]_u \\ & = \sum_{u \in \sum^n} \sum_{(i,j): s(i) = t(j) = u} \lambda^{l(i)} \lambda^{l(j)} \end{align*}$$

• $[\phin(s)]_n = \sum{i:s(i)=u} \lambda^{l(i)}$：长度 大于等于n的字符串集合$S$到特征空间 $\mathcal{H} = R^{\sum^n}$的映射，目标特征空间每维对应 一个字符串$u \in \sum^n$

• $\sum$：有限字符表

• $\sum^n$：$\sum$中元素构成，长度为n的字符串集合

• $u = s(i) = s(i1)s(i_2)\cdots s(i{|u|})$：字符串s的 子串u（其自身也可以用此方式表示）

• $i =(i1, i_2, \cdots, i{|u|}), 1 \leq i1 < i_2 < … < i{|u|} \leq |s|$：序列指标

• $l(i) = i_{|u|} - i_1 + 1 \geq |u|$：字符串长度，仅在 序列指标$i$连续时取等号（$j$同）

• $0 < \lambda \leq 1$：衰减参数

• 两个字符串s、t上的字符串核函数，是基于映射$\phi_n$的 特征空间中的内积

  • 给出了字符串中长度为n的所有子串组成的特征向量的余弦 相似度
  • 直观上，两字符串相同子串越多，其越相似，核函数值越大
  • 核函数值可由动态规划快速计算（只需要计算两字符串公共 子序列即可）

• 应用场合

  • 文本分类
  • 信息检索
  • 信物信息学

Langrangian Duality

拉格朗日对偶

• 考虑优化问题：找到$f(x)$满足约束的最好下界

  $$z^{*} = \min_{x} f(x) \\ \begin{align*} s.t. \quad & g_i(x) \leq 0, i=1,2,\cdots,m \\ & x \in X \end{align*}$$

• 考虑方程组

  $$\left \{ \begin{array}{l} f(x) < v \\ g_i(x) \leq 0, i=1,2,\cdots,m \end{array} \right.$$

  • 方程组无解：$v$是优化问题的一个下界

  • 方程组有解：则可以推出

    $$\forall \lambda \geq 0, \exists x, f(x) + \sum_{i=1}^m \lambda_ig_i(x) < v$$

    • 显然，取$g_1 + g_2 = 0, g_1(x) > 0$是反例，不能 推出原方程有解

  • 由以上方程组有解逆否命题：方程组无解充分条件如下

    $$\exists \lambda \geq 0, \min_{x} f(x) + \sum _{i=1}^m \lambda_ig_i(x) \geq v$$

• 由此方法推出的最好下界，即拉格朗日对偶问题

  $$v^{*} = \max_{\lambda \geq 0} \min_{x} f(x) + \sum_{i=1}^m \lambda_ig_i(x)$$

说明

• 拉格朗日对偶对实数域上的优化问题都存在，对目标函数、 约束函数都没有要求

• 强对偶定理：$v^{} = z^{}$，需要$f,g$满足特定条件才成立

  • 线性规划
  • 半正定规划
  • 凸优化

  • 即需要给约束条件加以限制，使得 $$\forall \lambda \geq 0, \exists x, f(x) + \sum_{i=1}^m \lambda_ig_i(x) < v$$ 是上述方程组有解的冲要条件

• 弱对偶定理：$v^{} \leq z^{}$，永远成立（以上即可证）

  • 通过弱对偶定理，可以得到原问题的一个下界
  • 对求解原问题有帮助，比如：分支界限法中快速求下界

• 对偶问题相关算法往往原问题算法在实际应用中往往更加有效

  • dual-simplex
  • primal-dual interior point method
  • augmented Lagrangian Method

原始问题

约束最优化问题

$$\begin{array}{l} \min_{x \in R^n} & f(x) \\ s.t. & c_i(x) \leq 0, i = 1,2,\cdots,k \\ & h_j(x) = 0, j = 1,2,\cdots,l \end{array}$$

Generalized Lagrange Function

• 引入Generalized Lagrange Function

  $$L(x, \alpha, \beta) = f(x) + \sum_{i=1}^k \alpha_i c_i(x) + \sum_{j=1}^l \beta_j h_j(x)$$

  • $x=(x_1, x_2, \cdots, x_n) \in R^n$
  • $\alpha_i \geq 0, \beta_j$：拉格朗日乘子

• 考虑关于x的函数

  $$\theta_P(x) = \max_{\alpha, \beta: \alpha_i \geq 0} L(x, \alpha, \beta)$$

  • $P$：primal，原始问题

  • 若x满足原始问题的两组约束条件，则$\theta_P(x)=f(x)$

  • 若x违反等式约束j，取$\beta_j \rightarrow \infty$， 则有$\theta_P(x) \rightarrow \infty$

  • 若x违反不等式约束i，取$\alpha_i \rightarrow \infty$ ，则有$\theta_P(x) \rightarrow \infty$

  则有

  $$\theta_P(x) = \left \{ \begin{array}{l} f(x), & x 满足原始问题约束条件 \\ +\infty, & 其他 \end{array} \right.$$

• 则极小化问题，称为广义拉格朗日函数的极小极大问题

  $$\min_x \theta_P(x) = \max_{\alpha, \beta: \alpha_i \geq 0} L(x, \alpha, \beta)$$

  与原始最优化问题等价，两问题最优值相同，记为

  $$p^{*} = \min_x \theta_P(x)$$

对偶问题

• 定义

  $$\theta_D (\alpha, \beta) = \min_x L(x, \alpha, \beta)$$

• 再考虑极大化$\theta_D(\alpha, \beta)$，得到广义拉格朗日 函数的极大极小问题，即

  $$\max_{\alpha, \beta: \alpha \geq 0} \theta_D(\alpha, \beta) = \max_{\alpha, \beta: \alpha \geq 0} \min_x L(x, \alpha, \beta)$$

  表示为约束最优化问题如下

  $$\begin{align*} \max_{\alpha, \beta} & \theta_D(\alpha, \beta) = \max_{\alpha, \beta} \min_x L(x, \alpha, \beta) \\ s.t. & \alpha_i \geq 0, i=1,2,\cdots,k \end{align*}$$

  称为原始问题的对偶问题，其最优值定义记为

  $$d^{*} = \max_{\alpha, \beta: \alpha \geq 0} \theta_D(\alpha, \beta)$$

原始、对偶问题关系

定理1

• 若原始问题、对偶问题都有最优值，则 $$d^{*} = \max_{\alpha, \beta: \alpha \geq 0} \min_x L(x, \alpha, \beta) \leq \min_x \max_{\alpha, \beta: \alpha \geq 0} L(x, \alpha, \beta) = p^{*}$$

• $\forall x, \alpha, \beta$有

  $$\theta_D(\alpha, \beta) = \min_x L(x, \alpha, \beta) \leq L(x, \alpha, \beta) \leq \max_{\alpha, \beta: \alpha \geq 0} = \theta_P(x)$$

  即

  $$\theta_D(\alpha, \beta) \leq \theta_P(x)$$

• 而原始、对偶问题均有最优值，所以得证

• 设$x^{}$、$\alpha^{}, \beta^{}$分别是原始问题、对偶 问题的可行解，且$d^{} = p^{*}$，则其分别是原始问题、 对偶问题的最优解

思想：最速下降&牛顿

对目标函数$f(x)$在$x^{(1)}$进行展开

$$f(x) = f(x^{(1)}) + \nabla f(x^{(1)})(x - x^{(1)})+ \frac 1 2 \nabla^2 f(x^{(1)})(x - x^{(1)})^2 + o((x - x^{(1)})^2)$$

• 最速下降法：只保留一阶项，即使用线性函数近似原目标函数
• Newton法：保留一阶、二阶项，即使用二次函数近似

• 利用近似函数求解元素问题极小值

  • 最速下降法：线性函数无极值，需要确定步长、迭代
  • Newton法：二次函数有极值，直接求导算出极值、迭代

• 最速下降法

  • 只考虑一阶导：甚至说根本没有考虑拟合原目标函数

• Newton法

  • 考虑二阶导：每步迭代还考虑了二阶导，即当前更新完毕 后，下一步能够更好的更新（二阶导的意义）
  • 甚至从后面部分可以看出，Newton法甚至考虑是全局特征， 不只是局部性质（前提目标函数性质足够好）
  • 二次函数拟合更接近函数极值处的特征

最速下降算法

思想

• 设$x=x(t)$为最优点$x$从初始点、沿负梯度方向经过的曲线， 则有

  $$\left \{ \begin{array}{l} & \frac {dx(t)} {dt} = -\nabla f(x(t)) \\ & x(t_1) = x^{(1)} \end{array} \right.$$

  • $t_1, x^{(1)}$：初始时刻、初始位置

• 可以证明，$x(t)$解存在，且$t \rightarrow \infty$时，有 $x(t) \rightarrow x^{ * }$，即得到无约束问题最优解

• 但微分方程组求解可能很麻烦，可能根本无法求解

  • 考虑将以上曲线离散化，每次前进到“不应该”前进为止
  • 然后更换方向，逐步迭代得到最优解

算法

• 搜索方向最速下降方向：负梯度方向
• 终止准则：$\nabla f(x^{(k)})=0$

1. 取初始点$x^{(1)}$，置k=1

2. 若$\nabla f(x^{(k)})=0$，则停止计算，得到最优解， 否则置

   $$d^{(k)} = -\nabla f(x^{(k)})$$

   以负梯度作为前进方向

3. 一维搜索，求解一维问题

   $$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$$

   得$\alpha_k$前进步长，置

   $$x^{(k+1)} = x^{(k)} + \alpha_k d^{(k)}$$

4. 置k=k+1，转2

• 最速下降算法不具有二次终止性

叠加惯性

模拟物体运动时惯性：指数平滑更新步长

Momentum

冲量方法：在原始更新步上叠加上次更新步，类似指数平滑

$$v^{(t)} = \gamma v^{(t-1)} + (1 - \gamma) \eta \bigtriangledown_\theta L(\theta^{(t-1)}) \\ \theta^{(t)} = \theta^{(t-1)} - v^{(t)}$$

• $v^{(t)}$：第$t$步时第k个参数更新步
• $L(\theta)$：往往是batch损失函数

• 更新参数时，一定程度保持上次更新方向
• 可以在一定程度上保持稳定性，学习速度更快
• 能够越过部分局部最优解

Nesterov Momentum

NGA：在使用冲量修正最终方向基础上，使用冲量对当前 参数位置进行修正，即使用“未来”位置计算梯度

• 先使用冲量更新一步
• 再在更新后位置计算新梯度进行第二步更新

$$v^{(t)} = \gamma v^{(t-1)} + \eta \bigtriangledown_\theta L(\theta^{(t-1)} - \gamma v^{(t-1)}) \\ \theta^{(t)} = \theta^{(t-1)} - v^{(t)}$$

动态学习率

• 学习率太小收敛速率缓慢、过大则会造成较大波动
• 在训练过程中动态调整学习率大小较好

• 模拟退火思想：达到一定迭代次数、损失函数小于阈值时，减小 学习速率

Vanilla Gradient Descent

每次迭代减小学习率$\eta$

$$\eta^{(t)} = \frac \eta {\sqrt {t+1}} \\ \theta^{(t)} = \theta^{(t-1)} - \eta^{(t)} \bigtriangledown_\theta L(\theta^{(t-1)})$$

• 学习率逐渐减小，避免学习后期参数在最优解附近反复震荡

Adagrad

adaptive gradient：训练中不同参数学习率随着迭代次数、 梯度动态变化，使得参数收敛更加平稳

$$v^{(t)}_k = \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ \theta^{(t)}_k = \theta^{(t-1)}_k - \frac \eta {\sqrt {\sum_{i=0}^{t-1} (v^{(i)}_k)^2 + \epsilon}} v^{(t)}_k$$

• $\epsilon$：fuss factor，避免分母为0
• $\theta^{(t)}_k$：第t轮迭代完成后待估参数第k个分量 （之前未涉及参数间不同，统一为向量）

• 特点

  • 较大梯度参数真正学习率会被拉小；较小梯度真正学习率 参数被拉小幅度较小
  • 可以和异步更新参数结合使用，给不常更新参数更大学习率

• 缺点

  • 在训练后期，分母中梯度平方累加很大，学习步长趋于0， 收敛速度慢（可能触发阈值，提前结束训练）

RMSprop

root mean square prop：指数平滑更新学习率分母

$$v^{(t)}_k = \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ \theta^{(t)}_k = \theta^{(t-1)}_k - \frac \eta {\sqrt { \gamma \sum_{i=1}^{t-1}(v^{(i)}_k)^2 + (1 - \gamma)((v^{(t)})^2 + \epsilon} } v^{(t)}$$

• 赋予当前梯度更大权重，减小学习率分母，避免学习速率下降 太快

Adam

adptive moment estimation：指数平滑更新步、学习率分母

$$\begin{align*} v^{(t)}_k & = \gamma_1 v^{(t-1)}_k + (1 - \gamma_1) \bigtriangledown_{\theta_k} L(\theta^{(t-1)}) \\ s^{(t)}_k & = \gamma_2 s^{(t-1)}_k + (1 - \gamma_2) \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \hat{v^{(t)}_k} & = \frac {v^{(t)}_k} {1 - \gamma_1^t} \\ \hat{s^{(t)}_k} & = \frac {s^{(t)}_k} {1 - \gamma_2^t} \\ \theta^{(t)}_k & = \theta^{(t-1)}_k - \frac \eta {\sqrt{\hat{s^{(t)}_k} + \epsilon}} \hat{v^{(t)}_k} \end{align*}$$

• $\gamma_1$：通常为0.9
• $\gamma_2$：通常为0.99
• $\hat{v^{(t)}_k} = \frac {v^{(t)}_k} {1 - \gamma_1^t}$ ：权值修正，使得过去个时间步，小批量随机梯度权值之和为1

• 利用梯度的一阶矩$v^{(t)}$、二阶矩$s^{(t)}$动态调整每个 参数学习率

• 类似于mommentum、RMSprop结合

• 经过偏执矫正后，每次迭代学习率都有确定范围，参数比较平稳

Adadelta

指数平滑更新学习率（分子）、学习率分母

$$\begin{align*} s^{(t)}_k & = \gamma_1 s^{(t-1)}_k + (1 - \gamma_1) \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \hat{v^{(t)}_k} & = \sqrt {\frac {\Delta \theta^{(t-1)}_k + \epsilon} {s^{(t)}_k + \epsilon}} \bigtriangledown_{\theta_k} L(\theta^{(t-1)})^2 \\ \Delta \theta^{(t)}_k & = \gamma_1 \Delta \theta^{(t-1)}_k + (1 - \gamma_1) \hat{v^{(t)}_k}^2 \\ \theta^{(t)}_k & = \theta^{(t)}_k - \hat{v^{(t)}_k} \end{align*}$$

• $s, \Delta \theta$共用超参$\gamma_1$

• 在RMSprop基础上，使用$\sqrt {\Delta \theta}$作为学习率
• $\hat v$：中超参$\gamma_1$在分子、分母“抵消”，模型对 超参不敏感

样本量

Singular Loss/Stocastic Gradient Descent

SGD：用模型在某个样本点上的损失极小化目标函数、计算梯度、 更新参数

• 单点损失度量模型“一次”预测的好坏

  • 代表模型在单点上的优劣，无法代表模型在总体上性质
  • 具有很强随机性

• 单点损失不常用，SGD范围也不局限于单点损失

• 损失函数具体参见ml_xxxxx

全局估计

全局损失：用模型在全体样本点上损失极小化目标函数、计算梯度、 更新参数

$$\theta^{(t)} = \theta^{(t-1)} - \eta \bigtriangledown_\theta L_{total}(\theta_{(t-1)})$$

• $\theta^{(t)}$：第t步迭代完成后待估参数
• $\eta$：学习率
• $L{total}(\theta) = \sum{i=1}^N L(\theta, x_i, y_i)$： 训练样本整体损失
• $N$：训练样本数量

• 若损失函数有解析解、样本量不大，可一步更新（计算） 完成（传统参数估计场合）

  • 矩估计
  • 最小二乘估计
  • 极大似然估计

• 否则需要迭代更新参数

  • 样本量较大场合
  • 并行计算

Mini-Batch Loss

mini-batch loss：用模型在某个batch上的损失极小化目标函数、 计算梯度、更新参数

$$\theta^{(t)} = \theta^{(t-1)} - \eta \bigtriangledown_\theta L_{batch}(\theta^{(t-1)})$$

• $L{batch}(\theta)=\sum{i \in B} L(\theta, x_i, y_i)$： 当前batch整体损失
• $B$：当前更新步中，样本组成的集合batch

• batch-loss是模型在batch上的特征，对整体的代表性取决于 batch大小

  • batch越大对整体代表性越好，越稳定；越小对整体代表 越差、不稳定、波动较大、难收敛
  • batch大小为1时，就是SGD
  • batch大小为整个训练集时，就是经验（结构）风险

• batch-loss是学习算法中最常用的loss，SGD优化常指此

  • 实际中往往是使用batch-loss替代整体损失，表示经验风险 极小化
  • batch-loss同样可以带正则化项，表示结构风险极小化
  • 损失极值：SVM（几何间隔最小）

优点

• 适合样本量较大、无法使用样本整体估计使用
• 一定程度能避免局部最优（随机batch可能越过局部极值）
• 开始阶段收敛速度快

缺点

• 限于每次只使用单batch中样本更新参数，batch-size较小时， 结果可能不稳定，往往很难得到最优解

• 无法保证良好的收敛性，学习率小收敛速度慢，学习率过大 则损失函数可能在极小点反复震荡

• 对所有参数更新应用相同学习率，没有对低频特征有优化 （更的学习率）

• 依然容易陷入局部最优点

Newton法

思想

• 若$x^{ * }$是无约束问题局部解，则有

  $$\nabla f(x^{ * }) = 0$$

  可求解此问题，得到无约束问题最优解

• 原始问题是非线性，考虑求解其线性逼近，在初始点$x^{(1)}$ 处泰勒展开

  $$\nabla f(x) \approx \nabla f(x^{(1)}) + \nabla^2 f(x^{(1)})(x - x^{(1)})$$

  解得

  $$x^{(2)} = x^{(1)} - (\nabla^2 f(x^{(1)}))^{-1} \nabla f(x^{(1)})$$

  作为$x^{ * }$的第二次近似

• 不断迭代，得到如下序列

  $$x^{(k+1)} = x^{(k)} + d^{(k)}$$

  • $d^{(k)}$：Newton方向，即以下方程解 $$\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$$

算法

• 初始点 $x^{(1)}$、精度要求 $\epsilon$，置 $k=1$

• 考虑 $|\nabla f(x^{(k)})| \leq \epsilon$

  • 若满足，则停止计算，得到最优解 $x^{(k)}$

  • 否则求解如下方程，得到 $d^{(k)}$

    $$\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$$

• 如下设置，并转2

  $$x^{(k+1)} = x^{(k)} + d^{(k)}, k = k+1$$

特点

• 优点

  • 产生点列 ${x^{k}}$ 若收敛，则具有二阶收敛速率
  • 具有二次终止性，事实上对正定二次函数，一步即可收敛

• 缺点

  • 可能会在某步迭代时目标函数值上升
  • 当初始点 $x^{(1)}$ 距离最优解 $x^{ * }$ 时，产生的点列 可能不收敛，或者收敛到鞍点
  • 需要计算 Hesse 矩阵
    • 计算量大
    • Hesse 矩阵可能不可逆，算法终止
    • Hesse 矩阵不正定，Newton 方向可能不是下降方向

阻尼/修正 Newton 法

• 克服 Newton 法目标函数值上升的缺点
• 一定程度上克服点列可能不收敛缺点

算法

• 初始点 $x^{(1)}$、精度要求 $\epsilon$，置 $k=1$

• 考虑 $|\nabla f(x^{(k)})| \leq \epsilon$

  • 若满足，停止计算，得到最优解 $x^{(k)}$
  • 否则求解如下方程得到 $d^{(k)}$ $$\nabla^2 f(x^{(k)}) d = -\nabla f(x^{(k)})$$

• 一维搜索，求解一维问题

  $$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$$

  得到 $\alpha_k$，如下设置并转2

  $$x^{(k+1)} = x^{(k)} + \alpha_k d^{(k)}, k = k+1$$

其他改进

• Newton 法、修正 Newton 法的改进方向
  • 结合最速下降方向修正迭代方向
  • Hesse 矩阵不正定情形下的替代

结合最速下降方向

• 将 Newton 方向和最速下降方向结合

• 设 $\theta_k$ 是 $$ 之间夹角，显然希望 $\theta < \frac \pi 2$

• 则置限制条件 $\eta$，取迭代方向

  $$d^{(k)} = \left \{ \begin{array}{l} d^{(k)}, & cos\theta_k \geq \eta \\ -\nabla f(x^{(k)}), & 其他 \end{array} \right.$$

Negative Curvature

• 当 Hesse 矩阵非正定时，选择负曲率下降方向 $d^{(k)}$（一定存在）

• Hesse 矩阵非正定时，一定存在负特征值、相应特征向量 $u$

  • 取负曲率下降方向作为迭代方向

    $$d^{(k)} = -sign(u^T \nabla f(x^{(k)})) u$$

  • $x^{(k)}$ 处负曲率方向 $d^{(k)}$ 满足

    $${d^{(k)}}^T \nabla^2 f(x^{(k)}) d^{(k)} < 0$$

修正 Hesse 矩阵

• 取迭代方向 $d^{(k)}$ 为以下方程的解

  $$(\nabla^2 f(x^{(k)}) + v_k I) d = -\nabla f(x^{k})$$

• $v_k$：大于 $\nabla^2 f(x^{(k)})$ 最大负特征值绝对值

综述

拟Newton法/变度量法：不需要求解Hesse矩阵，使用一阶导构造 二阶信息的近似矩阵

• 使用迭代过程中信息，创建近似矩阵$B^{(k)}$代替Hesse矩阵

• 用以下方程组替代Newton方程，其解$d^{(k)}$作为搜索方向

  $$B^{(k)} d = - \triangledown f(x^{(k)})$$

思想

• 考虑$\triangledown f(x)$在$x^{(k+1)}$处泰勒展开

  $$\triangledown f(x) \approx \triangledown f(x^{(k+1)}) + \triangledown^2 f(x^{(k+1)})(x - x^{(k+1)})$$

• 取$x = x^{(k)}$，有

  $$\begin{align*} \triangledown f(x^{(k+1)}) - \triangledown f(x^{(k)}) & \approx \triangledown^2 f(x^{(x+1)}) (x^{(k+1) } - x^{(k)}) \\ \triangledown^2 f(x^{k+1}) s^{(k)} & \approx y^{(k)} \end{align*}$$

  • $s^{(k)} = x^{(k+1)} - x^{(k)}$
  • $y^{(k)} = \triangledown f(x^{(k+1)}) - \triangledown f(x^{(k)})$

• 要求$B^{(k)}$近似$\triangledown^2 f(x^{(k)})$，带入并将 $\approx$改为$=$，得到拟Newton方程

  $$B^{(k+1)} s^{(k)} = y^{(k)}$$

  并假设$B^{(k)}$对称

• 拟Newton方程不能唯一确定$B^{(k+1)}$，需要附加条件，自然 的想法就是$B^{(k+1)}$可由$B^{(k)}$修正得到，即

  $$B^{(k+1)} = B^{(k)} + \Delta B^{(k)}$$

  且修正项$\Delta B^{(k)}$具有“简单形式”

Hesse矩阵修正

对称秩1修正

认为简单指矩阵秩小：即认为$\Delta B^{(k)}$秩为最小值1

• 设$\Delta B^{(k)} = u v^T$，带入有

  $$\begin{align*} y^{(k)} & = B^{(k+1)} s^{(k)} \\ & = B^{(k)} s^{(k)} + (v^T s^{(k)}) u \\ y^{(k)} - B^{(k)} s^{(k)} & = (v^T s^{(k)}) u \end{align*}$$
  • 这里有的书会设$\Delta B^{(k)} = \alpha u v^T$， 其实对向量没有必要
  • $v^T s^{(k)}$是数，所以$u$必然与共线，同理也没有必要 考虑系数，直接取相等即可
  • 而且系数不会影响最终结果

• 可取$u = y^{(k)} - B^{(k)} s{(k)}$，取$v$满足 $v^T s^{(k)} = 1$

• 由$B^{(k)}$的对称性、并希望$B^{(k+1)}$保持对称，需要 $u, v$共线，则有

  $$\begin{align*} v & = \lambda u = \lambda (y^{(k)} - B^{(k)} s^{(k)}) \\ 1 & = \lambda (y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)} \end{align*}$$

• 得到$B^{(k)}$的对称秩1修正公式

  $$B^{(k+1)} = B^{(k)} + \frac {(y^{(k) - B^{(k)} s^{(k)}}) (y^{(k)} - B^{(k)} s^{(k)})^T} {(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)}}$$

算法

1. 初始点$x^{(1)}$、初始矩阵$B^{(1)} = I$、精度要求 $\epsilon$、置$k=1$

2. 若$|\triangledown f(x^{(k)})| \leq \epsilon$，停止计算 ，得到解$x^{(k)}$，否则求解以下方程得到$d^{(k)}$

   $$B^{(k)} d = -\triangle f(x^{(k)})$$

3. 一维搜索，求解

   $$\arg\min_{\alpha} \phi(\alpha)=f(x^{(k)} + \alpha d^{(k)})$$

   得到$\alpha_k$，置$x^{(k+1)}=x^{(k)} + \alpha_k d^{(k)}$

4. 修正$B^{(k)}$

   $$\begin{align*} s^{(k)} & = x^{(k+1)} - x^{(k)} \\ y^{(k)} & = \triangledown f(x^{(k+1)}) - \triangledown f(x^{(k)}) \\ B^{(k+1)} & = B^{(k)} + \frac {(y^{(k) - B^{(k)} s^{(k)}}) (y^{(k)} - B^{(k)} s^{(k)})^T} {(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)}} \end{align*}$$

5. 置$k = k+1$，转2

特点

• 缺点

  • 要求$(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)} \neq 0$， 否则无法继续计算

  • 不能保证正定性传递，只有 $(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)} > 0$才能保证 $B^{(k+1)}$也正定

  • 即使$(y^{(k)} - B^{(k)} s^{(k)})^T s^{(k)} > 0$， 也可能很小，容易产生较大的舍入误差

对称秩2修正

• 为克服秩1修正公式缺点，考虑$\Delta B^{(k)}$秩为2，设

  $$\Delta B^{(k)} = u^{(1)} (v^{(1)})^T + u^{(2)} (v^{(2)})^T$$

• 带入拟Newton方程有

  $$B^{(k)} s^{(k)} + ((v^{(1)})^T s^{(k)}) u^{(1)} + ((v^{(2)})^T s^{(k)}) u^{(2)} = y^{(k)}$$

• 类似的取

  $$\left \{ \begin{array}{l} u^{(1)} = y^{(k)} \\ (v^{(1)})^T s^{(k)} = 1 \end{array} \right.$$ $$\left \{ \begin{array}{l} u^{(2)} = -B^{(k)} s^{(k)} \\ (v^{(2)})^T s^{(k)} = 1 \end{array} \right.$$

• 同秩1公式保持对称性推导，得到对称秩2修正公式/BFGS公式

  $$B^{(k+1)} = B^{(k)} - \frac {B^{(k)} s^{(k)} (s^{(k)})^T B^{(k)}} {(s^{(k)})^T B^{(k)} s^{(k)}} + \frac {y^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}}$$

BFGS算法

类似同秩1修正算法，仅第4步使用对称秩2修正公式

Hesse逆修正

对称秩2修正

• 考虑直接构造近似于$(\triangledown^2 f(x^{(k)}))^{-1}$的 矩阵$H^{(k)}$

• 这样无需求解线性方程组，直接计算

  $$d^{(k)} = -H^{(k)} \triangledown f(x^{(k)})$$

• 相应拟Newton方程为

  $$H^{(k+1)} y^{(k)} = s^{(k)}$$

• 可得$H^{(k)}$的对称秩1修正公式

  $$H^{(k+1)} = H^{(k)} + \frac {(s^{(k)} - H^{(k)} y^{(k)}) (s^{(k)} - H^{(k)} y^{(k)})T} {(s^{(k)} - H^{(k)} y^{(k)})^T y^{(k)}}$$

• 可得$H^{(k)}$的对称秩2修正公式/DFP公式

  $$H^{(k+1)} = H^{(k)} - \frac {H^{(k)} y^{(k)} (y^{(k)})^T H^{(k)}} {(y^{(k)})^T H^{(k)} y^{(k)}} + \frac {s^{(k)} (s^{(k)})^T} {(s^{(k)})^T y^{(k)}}$$

DFP算法

类似BFGS算法，只是

• 使用$H^{(k)}$计算更新方向
• 使用$H^{(k)}$的对称秩2修正公式修正

• 对正定二次函数，BFGS算法和DFP算法效果相同
• 对一般可微（非正定二次函数），一般认为BFGS算法在收敛性质 、数值计算方面均由于DFP算法

Hesse逆的BFGS算法

• 考虑

  $$\begin{align*} B^{(k+1)} & = B^{(k)} + u^{(1)} (v^{(1)})^T + u^{(2)} (v^{(2)})^T \\ H^{(k+1)} & = (B^{(k+1)})^{-1} \\ & = (B^{(k)} + u^{(1)} (v^{(1)})^T + u^{(2)} (v^{(2)})^T)^{-1} \\ \end{align*}$$

• 两次利用Sherman-Morrison公式，可得

  $$H^{(k+1)} = (I - \frac {s^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}}) H^{(k)} (I - \frac {s^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}})^T + \frac {s^{(k)} (s^{(k)})^T} {(y^{(k)})^T s^{(k)}}$$

todo

• 还可以进一步展开

  $$H^{(k+1)} = H^{(k)} + (\frac 1 {(s^{(k)})^T y^{(k)}} + \frac {(y^{(k)})^T H^{(k)} y^{(k)}} {((s^{(k)})^T y^{(k)})^2}) s^{(k)} (s^{(k)})^T - \frac 1 {(s^{(k)})^T y^{(k)}} (H^{(k)} y^{(k)} (s^{(k)})^T + s^{(k)} (y^{(k)})^T H^{(k)})$$

变度量法的基本性质

算法的下降性

定理1

• 设$B^{(k)}$（$H^{(k)}$）是正定对称矩阵，且有 $(s^{(k)})^T y^{(k)} > 0$，则由BFGS（DFS）公式构造的 $B^{(k+1)}$（$H^{(k+1)}$）是正定对称的

• 考虑$B^{(k)}$对称正定，有 $B^{(k)} = (B^{(k)})^{1/2} (B^{(k)})^{1/2}$

• 带入利用柯西不等式即可证

• 中间插入正定矩阵的向量内积不等式也称为广义柯西不等式

定理2

• 若$d^{(k)}$v是下降方向，且一维搜索是精确的，设 $B^{(k)}$（$H^{(k)}$）是正定对称矩阵，则有BFGS（DFP） 公式构造的$B^{(k+1)}$（$H^{(k+1)}$）是正定对称的

• 精确一维搜索$(d^{(k)})^T \triangledown f(x^{(k+1)}) = 0$
• 则有$(s^{(k)})^T y^{(k)} > 0$

定理3

• 若用BFGS算法（DFP算法）求解无约束问题，设初始矩阵 $B^{(1)}$（$H^{(1)}$）是正定对称矩阵，且一维搜索是精确的 ，若$\triangledown f(x^{(k)}) \neq 0$，则产生搜索方向 $d^{(k)}$是下降方向

• 结合上2个结论，数学归纳法即可

总结

• 若每步迭代一维搜索精确，或满足$(s^{(k)})^T y^{(k)} > 0$

  • 停止在某一稳定点
  • 或产生严格递减的序列${f(x^{(k)})}$

• 若目标函数满足一定条件我，可以证明变度量法产生的点列 ${x^{(k)}}$收敛到极小点，且收敛速率超线性

搜索方向共轭性

• 用变度量法BFGS（DFP）算法求解正定二次函数

$$
min f(x) = \frac 1 2 x^T G x + r^T x + \sigma
$$

若一维搜索是精确的，假设已经进行了m次迭代，则

• 搜索方向$d^{(1)}, \cdots, d^{(m)}$是m个非零的G共轭方向

• 对于$j = 1, 2, \cdots, m$，有

$$
B^{(m+1)} s^{(j)} = y^{(j)}
(H^{(m+1)} y^{(j)} = s^{(j)})
$$

且$m = n$时有吧

$$
B^{(n+1)} = G(H^{(n+1)} = G^{-1})
$$

变度量法二次终止

• 若一维搜索是精确的，则变度量法（BFGS、DFP）具有二次终止

• 若$\triangle f(x^{(k)}) = 0, k \leq n$，则得到最优解 $x^{(k)}$

• 否则得到的搜索方向是共轭的，由扩展空间子定理， $x^{(n+1)}$是最优解

共轭方向

• 设G为$n * n$阶正定对称矩阵，若$d^{(1)}, d^{(2)}$满足

  $$(d^{(1)})^T G d^{(2)} = 0$$

  则称$d^{(1)}, d^{(2)}$关于G共轭

• 类似正交方向，若$d^{(1)},\cdots,d^{(k)}(k \leq n)$关于 G两两共轭，则称其为G的k个共轭方向

• 特别的，$G=I$时，共轭方向就是正交方向

定理1

• 设目标函数为 $$f(w) = \frac 1 2 w^T w + r^T w + \sigma$$ $q^{(1)}, \cdots, q^{(k)}$是$k, k \leq n$个非零正交方向 ，从任意初始点$w^{(1)}$出发，依次沿着以上正交方向做 精确一维搜索，得到$w^{(1)}, \cdots, w^{(k+1)}$， 则$w^{(k+1)}$是$f(w)$在线性流形 $$\bar W_k = \{w = w^{(1)} + \sum_{i=1}^k \alpha_i q^{(i)} | -\infty < \alpha_i < +\infty \}$$ 上的唯一极小点，特别的k=n时，$w^{(n+1)}$是$f(w)$在整个 空间上的唯一极小点

• $\bar W_k$上的存在唯一极小点$\hat w^{(k)}$，在所有方向 都是极小点，所以有

  $$<\triangledown f(\hat w^{(k)}), q^{(i)}> = 0, i=1,2,..$$

• 将$\hat w^{(k)}$由正交方向表示带入梯度，求出系数表达式

• 解精确搜索步长，得到$w^{(k+1)}$系数表达式

扩展子空间定理

• 设目标函数为 $$f(w) = \frac 1 2 x^T G x + r^T x + \sigma$$ $d^{(1)}, \cdots, d^{(k)}$是$k, k \leq n$个非零正交方向 ，从任意初始点$x^{(1)}$出发，依次沿着以上正交方向做 精确一维搜索，得到$x^{(1)}, \cdots, x^{(k+1)}$， 则$x^{(k+1)}$是$f(x)$在线性流形 $$\bar x_k = \{x = x^{(1)} + \sum_{i=1}^k \alpha_i d^{(i)} | -\infty < \alpha_i < +\infty \}$$ 上的唯一极小点，特别的k=n时，$x^{(n+1)}$是$f(x)$在整个 空间上的唯一极小点

• 引进变换$w = \sqrt G x$即可证

• 在以上假设下，有 $$<\triangledown f(x^{(k+1)}), d^{(i)}> = 0, i=1,2...$$

Conjugate Gradient Method

共轭梯度法

对正定二次函数函数

$$f(x) = \frac 1 2 x^T G x + r^T x + \sigma$$

• 任取初始点$x^{(1)}$，若$\triangledown f(x^{(1)}) = 0$， 停止计算，得到极小点$x^{(1)}$，否则取

  $$d^{(1)} = -\triangledown f(x^{(1)})$$

• 沿着$d^{(1)}$方向进行精确一维搜索得到$x^{(2)}$，若 $\triangledown f(x^{(2)}) \neq 0$，令

  $$d^{(2)} = -\triangledown f(x^{(2)}) + \beta_1^{(2)} d^{(1)}$$

  且满足$(d^{(1)})^T G d^{(2)} = 0$，即二者共轭，可得

  $$\beta_1^{(2)} = \frac {(d^{(1)})^T G \triangledown f(x^{(2)})} {((d^{(1)})^T G d^{(1)})}$$
  • 这里$d^{(2)}$方向的构造方式是为类似构造后面$d^{(k)}$ ，得到能方便表示的系数
  • 类似于将向量组$\triangledown f(x^{(i)})$正交化

• 如此重复搜索，若$\triangledown f^(x^{i)}) \neq 0$，构造 $x^{(k)}$处搜索方向$d^{(k)}$如下

  $$\begin{align*} 0 & = (d^{(i)})^T G d^{(k)} \\ & = -(d^{(i)})T G \triangledown f(x^{(k)}) + \sum_{j=1}^{k-1} \beta_j^{(k)} (d^{(i)})^T G d^{(j)} \\ & = -(d^{(i)})^T G \triangledown f(x^{(k)}) + \beta_i^{(k)} (d^{(i)})^T G d^{(i)} \end{align*}$$

  可得

  $$\beta_i^{(k)} = \frac {(d^{(i)})^T G \triangledown f(x^{(k)})} {(d^{(i)})^T G d^{(i)}}$$

  此时$d^{(k)}$与前k-1个方向均关于G共轭，此k个方向是G的k个 共轭方向，由扩展空间子定理，$x^{(k+1)}$是整个空间上极小

计算公式简化

期望简化$d^{(k)}$的计算公式

• 由扩展子空间定理推论有 $\triangledown f(x^{(k)})^T d^{(i)} = 0, i=1,2…,k-1$ 结合以上$d^{(k)}$的构造公式，有

  $$\begin{align*} & \triangledown f(x^{(k)})^T \triangledown f(x^{(i)}) \\ = & \triangledown f(x^{(k)})^T ( -d^{(i)} + \beta_1^{(i)} d^{(1)} + \cdots + \beta_{i-1}^{(i)} d^{(i-1)} ) \\ = & 0, i=1,2,...,k-1 \end{align*}$$

• 则有

  $$\begin{align*} (d^{(i)})^T G \triangledown f(x^{(k)}) & = \triangledown f(x^{(k)})^T G d^{(i)} \\ & = \frac 1 {\alpha_i} \triangledown f(x^{(k)})^T G (x^{(i+1)} - x^{(i)}) \\ & = \frac 1 {\alpha_i} \triangledown f(x^{(k)})^T (\triangledown f(x^{(i+1)}) - \triangledown f(x^{(i)})) \\ & = 0, i=1,2,\cdots,k-2 \end{align*}$$

  • $d^{(k)} = \frac 1 {\alpha_i} x^{(i+1)} - x^{(i)}$

• 所以上述$d^{(k)}$构造公式可以简化为

  $$d^{(k)} = -\triangledown f(x^{(k)}) + \beta_{k-1} d^{(k-1)}$$

• 类似以上推导有

  $$\begin{align*} (d^{(k-1)})^T G \triangledown f(x^{(k)}) & = \frac 1 {\alpha_i} \triangledown f(x^{(k)})^T (\triangledown f(x^{(k)}) - \triangledown f(x^{(k-1)})) \\ & = \frac 1 {\alpha_i} \triangledown f(x^{(k)})^T \triangledown f(x^{(k)}) \\ \end{align*}$$ $$\begin{align*} (d^{(k-1)})^T G d^{(k-1)} & = \frac 1 {\alpha_i} (d^{(k-1)})^T (\triangledown f(x^{(k)}) - \triangledown f(x^{(k-1)})) \\ & = -\frac 1 {\alpha_i} (d^{(k-1)})^T \triangledown f(x^{(x-1)}) \\ & = -\frac 1 {\alpha_i} (\triangledown f(x^{(k-1)}) - \beta_{k-2}d^{(k-2)})^T \triangledown f(x^{(x-1)}) \\ & = -\frac 1 {\alpha_i} \triangledown f(x^{(k-1)})^T \triangledown f(x^{(k-1)}) \end{align*}$$

  最终的得到简化后系数$\beta_{k-1}, k>1$的PRP公式

  $$\beta_{k-1} = \frac {\triangledown f(x^{(k)})^T (\triangledown f(x^{(k)}) - \triangledown f(x^{(k-1)}))} {\triangledown f(x^{(k-1)})^T \triangledown f(x^{(k-1)})}$$

  或FR公式

  $$\beta_{k-1} = \frac {\|\triangledown f(x^{(k)})\|^2} {\|\triangledown f(x^{(k-1)}) \|^2}$$

• 以上推导虽然是根据正定二次函数得出的推导，但是仍适用于 一般可微函数

• $\beta _ {k-1}$给出两种计算方式，应该是考虑到目标函数 可能不是标准正定二次函数、一维搜索数值计算不精确性

• 将$\beta _ {k-1}$分子、分母推导到不同程度可以得到其他 公式

• Growder-Wolfe公式

  $$\beta_{k-1} = \frac {\triangledown f(x^{(k)})^T (\triangledown f(x^{(k)}) - \triangledown f(x^{(k-1)}))} {(d^{(k-1)})^T (\triangledown f(x^{(k)}) - \triangledown f(x^{(k-1)}))}$$

• Dixon公式

  $$\beta_{k-1} = \frac {\triangledown f(x^{(k)})^T \triangledown f(x^{(k)})} {(d^{(k-1)})^T \triangledown f(x^{(k-1)})}$$

FR/PRP算法

1. 初始点$x^{(1)}$、精度要求$\epsilon$，置k=1

2. 若$|\triangledown f(x^{(k)}) | \leq \epsilon$，停止 计算，得到解$x^{(k)}$，否则置

   $$d^{(k)} = -\triangledown f(x^{(k)}) + \beta_{k-1}d^{(k-1)}$$

   其中$\beta_{k-1}=0, k=1$，或由上述公式计算

3. 一维搜索，求解一维问题

   $$\arg\min_{\alpha} \phi(\alpha) = f(x^{(k)} - \alpha d^{(k)})$$

   得$\alpha_k$，置$x^{(k+1)} = x^{(k)} + \alpha_k d^{(k)}$

4. 置k=k+1，转2

• 实际计算中，n步重新开始的FR算法优于原始FR算法
• PRP算法中 $\triangledown f(x^{(k)}) \approx \triangledown f(x^{(k-1)})$ 时，有$\beta_{k-1} \approx 0$，即 $d^{(k)} \approx -\triangledown f(x^{(k)})$，自动重新开始
• 试验表明，对大型问题，PRP算法优于FR算法

共轭方向下降性

• 设$f(x)$具有连续一阶偏导，假设一维搜索是精确的，使用共轭 梯度法求解无约束问题，若$\triangledown f(x^{(k)}) \neq 0$ 则搜索方向$d^{(k)}$是$x^{(k)}$处的下降方向

• 将$d^{(k)}$导入即可

算法二次终止性

• 若一维搜索是精确的，则共轭梯度法具有二次终止性

• 对正定二次函数，共轭梯度法至多n步终止，否则

  • 目标函数不是正定二次函数
  • 或目标函数没有进入正定二次函数区域，

• 此时共轭没有意义，搜索方向应该重新开始，即令

  $$d^{(k)} = -\triangledown f(x^{(k)})$$

  即算法每n次重新开始一次，称为n步重新开始策略

综述

一维搜索/线搜索：单变量函数最优化，即求一维问题

$$\arg\min _ {\alpha} \phi(\alpha) = f(x^{(k)} + \alpha d^{(k)})$$

最优解的$\alpha_k$的数值方法

• exact line search：精确一维搜索，求得最优步长 $\alpha_k$使得目标函数沿着$d^{(k)}$方向达到极小，即

• inexact line search：非精确一维搜索，求得$\alpha_k$ 使得

  $$\begin{align*} f(x^{(k)} + \alpha_k d^{(k)}) & < f(x^{(k)}) \\ \phi(\alpha_k) & < \phi(0) \end{align*}$$

一维搜索基本结构

• 确定搜索区间
• 用某种方法缩小搜索区间
• 得到所需解

搜索区间

• 搜索区间：设$\alpha^{ }$是$\phi(\alpha)$极小点，若存在 闭区间$[a, b]$使得$\alpha^{ } \in [a, b]$，则称 $[a, b]$是$phi(\alpha)$的搜索区间

确定搜索区间的进退法

1. 取初始步长$\alpha$，置初始值

   $$\mu_3 = 0, \phi_3 = \phi(\mu_3), k = 0$$

2. 置

   $$\mu = \mu_3 + \alpha, \phi = \phi(\mu), k = k+1$$

3. 若$\phi < \phi_3$，置

   $$\mu_2 = \mu_3, \phi_2 = \phi_3 \\ \mu_3 = \mu, \phi_3 = \phi \\ \alpha = 2\alpha, k = k+1$$

4. 若k =1，置

   $$\mu_2 = mu, \phi_2 = \phi, \alpha = -\alpha$$

   转2，否则置

   $$\mu_1 = \mu_2, \phi_1 = \phi_2 \\ \mu_2 = \mu_3, \phi_2 = \phi_3 \\ \mu_3 = \mu, \phi_3 = \phi$$

   并令$a=min{\mu_1,\mu_3}, b=max{\mu_1,\mu_3}$，停止搜索

• 通常认为目标函数此算法得到搜索区间就是单峰函数

试探法

• 在搜索区间内选择两个点，计算目标函数值
  • 需要获得两个点取值才能判断极值点的所属区间
• 去掉函数值较大者至离其较近端点段

0.618法

1. 置初始搜索区间$[a, b]$，置精度要求$\epsilon$，计算左右 试探点

   $$\begin{align*} a_l & = a + (1 - \tau)(b - a) \\ a_r & = a + \tau(b - a) \end{align*}$$

   其中$\tau = \frac {\sqrt 5 - 1} 2$，及相应函数值

   $$\begin{align*} \phi_l & = \phi(a_l) \\ \phi_r & = \phi(a_r) \end{align*}$$

2. 若$\phi_l<\phi_r$，置

   $$b= a_r, a_r = a_l, \phi_l = \phi_l$$

   并计算

   $$a_l = a + (1 - \tau)(b - a), \phi_l = \phi(a_l)$$

   否则置

   $$a = a_l, a_l = a_r, \phi_l = \phi_r$$

   并计算

   $$a_r = a + \tau(b - a), \phi_r = \phi(a_r)$$

3. 若$|b - a| \geq \epsilon$

   • 若$\phi_l < \phi_r$，置$\mu = a_l$
   • 否则置$\mu = \alpha_r$ 得到问题解$\mu$，否则转2

• 0.618法除第一次外，每次只需要计算一个新试探点、一个新 函数值，大大提高了算法效率
• 收敛速率线性，收敛比为$\tau = \frac {\sqrt 5 - 1} 2$常数

Fibonacci方法

1. 置初始搜索区间$[a, b]$，置精度要求$\epsilon$，选取分离 间隔$\sigma < \epsilon$，求最小正整数n，使得 $F_n > \frac {b - a} \epsilon$，计算左右试探点

   $\begin{align} al & = a + \frac {F{n-2}} {Fn} (b - a)\ a_r & = a + \frac {F{n-1}} {F_n} (b - a) \end{align}

2. 置n=n-1

3. 若$\phi_l < \phi_r$，置

   $$b = a_r, a_r = a_l , \phi_r = \phi_l$$

   • 若n>2，计算

     $$\begin{align*} a_l & = a + \frac {F_{n-2}} {F_n} (b - a) \\ \phi_r & = \phi(a_l) \end{align*}$$

   • 否则计算

     $$\begin{align*} a_l & = a_r - \sigma \\ \phi_l & = \phi(a_l) \end{align*}$$

4. 若$\phi_l \geq \phi_r$，置

   $$a = a_l, a_l = a_r , \phi_l = \phi_r$$

   • 若n>2，计算

     $$\begin{align*} a_l & = a + \frac {F_{n-1}} {F_n} (b - a) \\ \phi_r & = \phi(a_r) \end{align*}$$

   • 否则计算

     $$\begin{align*} a_r & = a_l + \sigma \\ \phi_r & = \phi(a_r) \end{align*}$$

5. 若n=1

   • 若$\phi_l < \phi_r$，置$\mu = a_r$
   • 否则置$\mu = a_r$

   得到极小点$\mu$，停止计算，否则转2

• Finonacci方法是选取实验点的最佳策略，即在实验点个数相同 情况下，最终的极小区间最小的策略

• Finonacci法最优性质可通过设最终区间长度为1，递推使得原始 估计区间最大的取实验点方式，得出

插值法

• 利用搜索区间上某点的信息构造插值多项式（通常不超过3次） $\hat \phi(\alpha)$
• 逐步用$\hat \phi(\alpha)$的极小点逼近$\phi(\alpha)$ 极小点$\alpha^{*}$

• $\phi^{ * }$解析性质比较好时，插值法较试探法效果好

三点二次插值法

思想

以过三个点$(\mu_1,\phi_1), (\mu_2,\phi_2), (\mu_3,\phi_3)$ 的二次插值函数逼近目标函数

$$\begin{align*} \hat \phi(\alpha) & = \phi_1 \frac {(\alpha - \mu_2) (\alpha - \mu_3)} {(\mu_1 - \mu_2)(\mu_1 - \mu_3)} \\ & + \phi_2 \frac {(\alpha - \mu_1) (\alpha - \mu_3)} {(\mu_2 - \mu_1)(\mu_2 - \mu_3)} \\ & + \phi_3 \frac {(\alpha - \mu_1) (\alpha - \mu_2)} {(\mu_3 - \mu_1)(\mu_3 - \mu_2)} \end{align*}$$

• 求导，得到$\hat \phi(\alpha)$的极小点

  $$\mu = \frac {2[\phi_1(\mu_2-\mu_3) + \phi_2(\mu_3-\mu_1) + \phi_3(\mu_1 - \mu_2)]} {[\phi_1 (\mu_2^2-\mu_3^2) + \phi_2(\mu_3^2-\mu_1^2) + \phi_3(\mu_1^2 - \mu_2^2)]}$$

• 若插值结果不理想，继续构造插值函数求极小点近似值

算法

1. 取初始点$\mu_1<\mu_2<\mu_3$，计算$\phi_i=\phi(\mu_i)$， 且满足$\phi_1 > \phi_2, \phi_3 > \phi_2$，置精度要求 $\epsilon$

2. 计算

   $$A = 2[\phi_1(\mu_2 - \mu_3) + \phi_2(\mu_3 - \mu_1) + \phi_3(\mu_1 - \mu_2)]$$
   • 若A=0，置$\mu = \mu_2, \phi = \phi_2$，停止计算， 输出$\mu, \phi$

3. 计算

   $$\mu = [\phi_1 (\mu_2^2 - \mu_3^2) + \phi_2(\mu_3^2 - \mu_1^2) + \phi_3(\mu_1^2 - \mu_2^2)] / A$$
   • 若$\mu<\mu_1 或 \mu>\mu_3,\mu \notin (\mu_1,\mu_3)$ ，停止计算，输出$\mu, \phi$

4. 计算$\phi = \phi(\mu)$，若$|\mu - \mu_2| < \epsilon$， 停止计算，得到极小点$\mu$

5. 若$\mu \in (\mu_2, \mu_3)$

   • 若$\phi < \phi_2$，置 $$\mu_1=\mu_2, \phi_1=\phi_2, \mu_2=\mu, \phi_2=\phi$$
   • 否则置 $$\mu_3 = \mu, \phi_3 = \phi$$

   否则

   • 若$\phi < \phi_2$，置

     $$\mu_3=\mu_2, \phi_3=\phi_2, \mu_2=\mu, \phi_2=\phi$$

   • 否则置

     $$\mu_1 = \mu, \phi_1 = \phi$$

6. 转2

两点二次插值法

思想

以$\phi(\alpha)$在两点处$\mu_1, \mu_2$函数值 $\phi_1=\phi(\mu_1)$、一点处导数值 $\phi_1^{‘}=\phi^{‘}(\mu_1) < 0$构造二次函数逼近原函数

$$\begin{align*} \hat \phi(\alpha) & = A(\alpha - \mu_1)^2 + B(\alpha - \mu_1) + C \\ A & = \frac {\phi_2 - \phi_1 - \phi_1^{'}(\mu_2 - \mu_1)} {(\mu_2 - \mu_1)^2} \\ B & = \phi_1^{'} \\ C & = \phi_1 \end{align*}$$

• 为保证$[\mu_1, \mu_2]$中极小点，须有 $\phi_2 > \phi_1 + \phi_1^{‘}(\mu_2 - \mu_1)$

• 求解，得到$\hat \phi (\mu)$极小值为

  $$\mu = \mu_1 - \frac {\phi_1^{'}(\mu_2 - \mu_1)^2} {2[\phi_2 - \phi_1 - \phi_1^{'}(\mu_2 - \mu_1)]}$$

• 若插值不理想，继续构造插值函数求极小点的近似值

算法

1. 初始点$\mu_1$、初始步长$d$、步长缩减因子$\rho$、精度要求 $\epsilon$，计算

   $$\phi_1 = \phi(\mu_1), \phi_2 = \phi_(\mu_2)$$

2. 若$\phi_1^{‘} < 0$，置$d = |d|$，否则置$d = -|d|$

3. 计算

   $$\mu_2 = \mu_1 + d, \phi_2 = \phi(\mu_2)$$

4. 若$\phi_2 \leq \phi_1 + \phi_1^{‘}(\mu_2 - \mu_1)$，置 $d = 2d$，转3

5. 计算

   $$\mu = \mu_1 - \frac {\phi_1^{'}(\mu_2 - \mu_1)^2} {2[\phi_2 - \phi_1 - \phi_1^{'}(\mu_2 - \mu_1)]} \\ \phi = \phi(\mu), \phi^{'} = \phi^{'}(\mu)$$

6. 若$|phi^{‘}| \leq \epsilon$，停止计算，得到极小点$\mu$， 否则置

   $$\mu_1 = \mu, \phi_1 = \phi, \phi_1^{'} = \phi^{'}, \alpha = \rho \alpha$$

• 其中通常取$d = 1, \rho = 0.1$

两点三次插值法

原理

以两点$\mu_1, \mu_2$处函数值$\phi_i = \phi(\mu_i)$和其导数值 $\phi_i^{‘} = \phi^{‘}(\mu_i)$，由Himiter插值公式可以构造 三次插值多项式$\hat \phi(\alpha)$

• 求导置0，得到$\hat \phi(\alpha)$极小点

  $$\begin{align*} \mu & = \mu_1 + (\mu_2 - \mu_1)(1 - \frac {\phi_2^{'} + w + z} {\phi_2^{'} - \phi_1^{'} + 2w}) \\ z & = \frac {3(\phi_2 - \phi_1)} {\mu_2 - \mu_1} - \phi_1^{'} - \phi_2^{'} \\ w & = sign(\mu_2 - \mu_1) \sqrt {z^2 - \phi_1^{'} \phi_2^{'}} \end{align*}$$

算法

1. 初始值$\mu_1$、初始步长$d$、步长缩减因子$\rho$、精度要求 $\epsilon$，计算

   $$\phi_1 = \phi(\mu_1), \phi_1^{'} = \phi^{'}(\mu_1)$$

2. 若$\phi_1^{‘} > 0$，置$d = -|d|$，否则置$d = |d|$

3. 置$\mu_2 = \mu_1 + \alpha$，计算

   $$\phi_2 = \phi(\mu_2), \phi_2^{'} = \phi^{'}(\mu_2)$$

4. 若$\phi_1^{‘} \phi_2{‘} > 0$，置

   $$d = 2d, \mu_1 = \mu_2, \phi_1 = \phi_2, \phi_1^{'} = \phi_2^{'}$$

   转3

5. 计算

   $$\begin{align*} \mu & = \mu_1 + (\mu_2 - \mu_1)(1 - \frac {\phi_2^{'} + w + z} {\phi_2^{'} - \phi_1^{'} + 2w}) \\ z & = \frac {3(\phi_2 - \phi_1)} {\mu_2 - \mu_1} - \phi_1^{'} - \phi_2^{'} \\ w & = sign(\mu_2 - \mu_1) \sqrt {z^2 - \phi_1^{'} \phi_2^{'}} \\ \phi & = \phi(\mu) \\ \phi^{'} = \phi^{'}(\mu) \end{align*}$$

6. 若$|\phi^{‘}| < \epsilon$，停止计算，得到极小点$\mu$， 否则置

   $$d = \rho d, \mu_1 = \mu, \phi_1 = \phi, \phi_1^{'} = \phi^{'}$$

   转2

• 通常取$d = 1, \rho = 0.1$

非精确一维搜索

• 对无约束问题整体而言，又是不要求得到极小点，只需要一定 下降量，缩短一维搜索时间，使整体效果最好

• 求满足$\phi(\mu) < \phi(0)$、大小合适的$\mu$

  • $\mu$过大容易不稳定
  • $\mu$过小速度慢

GoldStein方法

原理

• 预先指定精度要求$0< \beta_1 < \beta_2 < 1$

• 以以下不等式限定步长

  $$\begin{align*} \phi(\mu) & \leq \phi(0) + \mu\beta_1 \phi^{'}(0) \\ \phi(\mu) & \geq \phi(0) + \mu\beta_2 \phi^{'}(0) \end{align*}$$

算法

1. 初始试探点$\mu$，置$\mu{min} = 0, \mu{max} = \infty$， 置精度要求$0 < \beta_1 < \beta_2 < 1$

2. 对$\phi(mu)$

   • 若$\phi(\mu) > \phi(0) + \beta1 \phi^{‘}(0) \mu$， 置$\mu{max} = \mu$

   • 否则若$\phi(\mu) > \phi(0) + \beta_2 \phi^{‘}(0)\mu$ ，则停止计算，得到非精确最优解$\mu$

   • 否则置$\mu_{min} = \mu$

3. 若$\mu{max} < \infty$，置 $\mu = \frac 1 2 (\mu{min} + \mu{max})$，否则置 $\mu = 2 \mu{min}$

4. 转2

Armijo方法

Armijo方法是Goldstein方法的变形

• 预先取$M > 1, 0 < \beta_1 < 1$

• 选取$\mu$使得其满足以下，而$M\mu$不满足

  $$\phi(\mu) \leq \phi(0) + \mu \beta_1 \phi^{'}(0)$$

• M通常取2至10

Wolfe-Powell方法

• 预先指定参数$0 < \beta_1 < \beta_2 <1$

• 选取$\mu$满足

  $$\begin{align*} \phi(\mu) & \leq \phi(0) + \mu \beta_1 \phi^{'}(0) \\ \phi^{'}(\mu) & \geq \beta_2 \phi^{'}(0) \end{align*}$$

• 能保证可接受解中包含最优解，而Goldstein方法不能保证