图算法

总述

• 图的遍历算法：如何一次访问到网络中所有节点
• 最短路线算法：两个城市间最佳路线
• 有向图拓扑排序：课程、预备课程是否有矛盾
• All-Pairs Shortest-Paths Problem：完全最短路径问题，找到 每个顶点到其他所有顶点的距离

遍历算法

Depth-First Search

深度优先查找（DFS）

算法

• 从任意顶点开始访问图顶点，然后标记为已访问

• 每次迭代时，紧接着处理与当前顶点邻接的未访问顶点， 直到遇到终点，该顶点所有邻接顶点均已访问过

• 在终点上，算法沿着来路后退一条边，继续从那里访问未 访问顶点

• 后退到起始点，且起始点也是终点时，算法停止，这样 起始点所在的连通分量的所有顶点均已访问过

• 若存在未访问顶点，则必须从其中任一顶点开始重复上述

count = 0
	// 全局变量：访问次序（次数）
DFS(G)
	// 对给定图的深度优先查找遍历
	// 输入：图G=<V, E>
	// 输出：图G顶点按照DFS遍历第一次访问到的先后次序，
	//       未访问到标记未0
	for each vertex v in V do
		if v is marked with 0
			dfs(v)
dfs(v)
	// 递归访问所有和v相连接的未访问顶点，赋予count值
	count = count+1
	mark v with count
	for each vertex w in V adjecnt to v do
		if w is marked with 0
			dfs(w)

特点

• 算法效率非常高效，消耗时间和表示图的数据结构规模成正比

  • 邻接矩阵：遍历时间效率$\in \Theta(|V|^2)$
  • 邻接链表：遍历时间效率$\in \Theta(|V|+|E|)$

• 可以方便地用栈跟踪深度优先查找

  • 首次访问顶点，将顶点入栈
  • 当顶点成为终点时，将其出栈
  • 运行时就是实际上就是栈，所以深度优先可以直接利用递归 实现

• Depth-First Search Foreat：参见 algorithm/data_structure/graph

• DFS产生两种节点排列顺序性质不同，有不同应用

  • 入栈（首次访问顶点）次序
  • 出栈（顶点成为终点）次序

应用

• 检查图连通性：算法第一次停止后，是否所有顶点已经访问
• 检查图无环性：DFS是否包含回边
• 拓扑排序：见键值法
  • DFS节点出栈逆序就是拓扑排序的一个解（图中无回边， 即为有向无环图）
  • DAG中顶点v出栈前，不存在顶点u拥有到v的边，否则存在 回边，图不是DAG

Broad-First Search

广度优先查找（BFS）

算法

• 首先访问所有和初始顶点邻接的顶点

• 然后是离它两条边的所有未访问顶点

• 以此类推，直到所有与初始顶点在同一连通分类顶点均已访问

• 若存在未访问顶点，从图其他连通分量任意顶点开始

count = 0
	// 全局变量：访问次序（次数）
BFS(G)
	// 给定图广度优先查找变量
	// 输入：图G=<V, E>
	// 输出：图G的顶点按照被BFS遍历第一次访问到次序，
	//       未访问顶点标记未0
	for each vertax v in V do
		if v is marked with 0
			bfs(v)
bfs(v)
	// 访问所有和v相连接的顶点，赋count值
	count = count+1
	whilte queue is not empty do
		for each vertex w in V adjcent to the front vertex do
			if w is marked with 0
				count = count+1
				mark w with count
				add w to the queue
		remove the front vertex from the queue

特点

• 算法效率同DFS

  • 邻接矩阵：遍历时间效率$\in \Theta(|V|^2)$
  • 邻接链表：遍历时间效率$\in \Theta(|V|+|E|)$

• 使用队列可以方便地跟踪广度优先查找操作

  • 从遍历初始顶点开始，标记、入队
  • 每次迭代时，算法查找所有和队头顶点邻接未访问，标记 、入队、将队头顶点出队

• Breadth-First Search Forest：参见 algorithm/data_struture/graph

• BFS只产生顶点的一种排序，因为队列时FIFO结构，顶点入队、 出队次序相同

应用

• 和DFS一样可以检查图的连通性、无环性，但是无法用于比较 复杂的应用

• 求给定两个顶点间最短路径：从一顶点开始BFS遍历，访问到 另一节点结束（难以证明？）

有向图强连通分量

Kosaraju算法

考虑有向图中强连通分量之间不连通的情况

• 强连通分量之间没有边

  • 在任意连通分量中任意结点开始深度优先遍历

  • 访问完所有结点需要DFS次数就是强连通分量数量，每轮 DFS访问的点就是强连通分量中的顶点

• 强连通分量之间只有单向边

  • 将强连通分量视为单个结点，则整个图可以视为一个 靠连通分量间单向边连接的有向无环图

  • 从最底层强连通分量中任选结点开始进行DFS，则此轮DFS 只能访问当前连通分量中结点

  • 逆序依次在各强连通分量中选择结点进行DFS，则每轮DFS只 访问当前连通分量中结点（其下层连通分量已访问）

  • 直至所有结点访问完毕，则得到所有强连通分量，即每轮 进行DFS访问的结点

  • 以下图为例，从图中连通分量B中任意结点开始进行DFS， 则经过两轮DFS即能找所有强连通分量

    

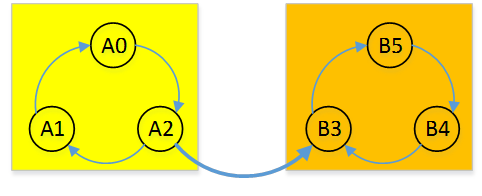
由以上分析

• 只需要保证底层强连通分量进行DFS优先搜索

• 也即在结点搜索优先级中，底层强连通分量中至少有一个结点 在其上层连通分量所有结点之前

• 可以利用原图的反向的DFS逆后序排列得到满足条件 的结点优先级序列

  

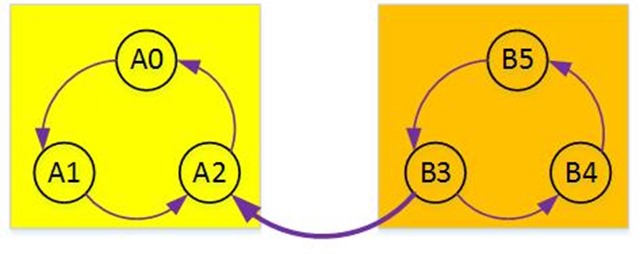
  • 若从反向图中最底层强连通分量某结点开始，则只能遍历 自身，反向图中其余连通分量位于其所有结点之前

  • 若从反向图中非最底层强连通分量某结点开始，则能依次 遍历其底层所有强连通分量中结点，且至少该结点位于其余 连通分量所有结点之前

• 逆后序排列参见algorithm/data_structure/graph

算法

• 对原图G每条路径求反，得到反向图$G^R$
• 对反向图$G^R$求解逆后序序列
• 按照逆序序列优先级，对原图G进行DFS，每棵DFS生成树就是 一个强连通分量

特点

• 算法效率
  • 时间效率$\in O(|V| + |E|)$
  • 算法需要对图进行两次DFS，速度较Tanjar算法更慢

Tarjan算法

Tarjan算法：基于图深度优先搜索的算法

• 为每个结点维护两个标记，通过此标记确定是否存在回路

  • DFN：深度优先搜索中搜索到次序
  • Low：通过回边能访问到的前驱被搜索到的次序

  • 还可以维护一个Flag，判断结点是否仍在DFS栈中

• 对图进行深度优先搜索

  • 未处理结点入栈，设置其DFN、Low被搜索到的次序

  • 对已处理结点，考虑到深度优先的搜索、退栈方式

    • 仍然在栈中，则肯定是栈顶元素前驱，连接边为回边， 存在栈顶节点到该前驱结点的回路

    • 不在栈中，该节点不是祖先结点，连接边为交叉边， 该结点已经在其他连通分量中出栈

  • 使用栈中前驱结点Low/DFN次序更新当前（栈顶）结点， 并递归更新，即使用子节点访问先驱次序更新父节点

• DFS回溯、退栈，考虑栈中每个结点DFN、Low

  • 若DFN[u] > Low[u]：结点u和其前驱之间有回路， 即其属于同一个强连通分量

  • 若DFN[u] == Low[u]：结点u和其前驱之间没有通路， 没有更多结点属于其所属强连通分量，以结点u为根子树 是一个强连通分量

    • 则从栈顶元素开始退栈直至结点u退栈，退栈的所有 元素构成强连通分量

• 每个强连通分量为深度优先搜索树中一个子树

$$Low[v] = \min\{DFN[v], Low[w], DFN[k]\}$$

• $w, (w, v) \in E$：顶点v的直接前驱
• $k, (v, k) \in E$：顶点v的祖先（即栈中结点）

算法

S = initStack()
DFN[MAX_VERTAX], Low[MAX_VERTEX]
index = 0
QList = InitList(Queue())

tarjan(u, E):
	// 比较DFS搜索次序、回边到达次序判断强连通分量
	// 输入：结点u，边集合E
	// 输出：强连通分量队列列表
	DFN[u] = Low[u] = ++ index
	S.push(u)
	for each (u, v) in E:
		if (v is not visited):
			tarjan(v)
			Low[u] = min(Low[u], Low[v])
			// 使用v找到的前驱更新u能找到前驱，递归更新
		else if (v in S):
			// 判断边是否为回边
			Low[u] = min(Low[u], DFN[v])
			// Low[u] = min(Low[u], Low[v])
				// 应该也行
	if(DFN[u] == Low[u]):
		Q = QList.next()
		repeat
			v = S.pop()
			Q.push(v)
		until (u == v)

特点

• 算法效率
  • 时间效率$\in O(|V|+|E|)$

关节点

类Tarjan算法

• 类似Tarjan算法为每个节点维护DFN、Low两个次序
  • 对非根结点v，存在其直接后继w有Low[w] >= DFN[v] ，则v为关节点
  • 对根节点，有两棵以上子树则为关节点

算法

此算法具体实现和Tarjan算法细节有差异

• 此算法中不需要使用栈保存访问过顶点中是前驱者
  • 连通无向图DFS只会有回边，已访问点必然是前驱结点
• 需要对根结点额外判断是否为关节点

DFN[MAX_VERTAX], Low[MAX_VERTEX]
index = 0
Q = InitQueue()

FindArticul(G):
	// 输入：无向连通图G
	// 输出：关节点队列
	vroot = G.V.pop()
	TarjanArticul(vroot, G)
	for(v in G.V if v not visited)
		// 根节点有两棵及以上子树
		TarjanAricul(vroot, G)
		Q.push(vroot)
		// 根节点也是关节点
	return Q

TarjanArticul(u, G):
	// 比较DFS搜索次序、回边到达次序判断关节点
	// 输入：结点u，无向连通图G
	// 输出：关节点队列
	DFN[u] = Low[u] = ++ index
	for each (u, v) in G.E:
		if (v is not visited):
			tarjan(v)
			Low[u] = min(Low[u], Low[v])
			// 使用v找到的前驱更新u能找到前驱，递归更新
		else:
			Low[u] = min(Low[u], DFN[v])
			// Low[u] = min(Low[u], Low[v])
				// 应该也行
	for(v connected by u)
		if(Low[v] <= DFN[u])
			Q.push(u)
	return Q

无权路径

路径数量

图中顶点i到顶点j之间长度为k的不同路径数量为$A^k[i, j]$

• A为图的邻接矩阵
• 可以使用数学归纳法证明
• 对无向、有向图均适用

Warshall算法

Warshall算法：生成有向图传递闭包

• 构造n+1个n阶布尔矩阵$R^{(k)}, k=0,1,\cdots, n$

  • $R^{(k)}_{ij}=1$：顶点i、j直接存在中间顶点编号 不大于k的有效路径

  • $R^{(0)}$：邻接矩阵，顶点直接连接

  • $R^{(k)}, 0<k<n$：路径中间顶点编号最大为k

  • $R^{(n)}$：传递闭包，允许所有类型路径

  • 后继矩阵相对前趋，允许作为路径上顶点增加，可能包含 1数量更多

• 考虑$R^{(k)}$通过直接前趋$R^{(k-1)}$计算得到

  • $R^{(k-1)}$中已有路径在$R^{(k)}$保留

  • 考虑$R^{(k)}$相较于$R^{(k-1)}$新增$r_{ij}=1$

    • 表示顶点i、j之间存在包含k的路径

    • 若k在路径中出现多次，则将删除回路，得到新路径

    • 则存在ik和kj之间路径满足中间顶点编号小于k，即在 $R^{(k-1)}$中有$r{ik}=1, r{kj}=1$

算法

• 若元素$r_{ij}$在$R^{(k-1)}$中为1，则在$R^{(k)}$也是1

• 若元素$r{ij}$在$R^{(k-1)}$中为0，当且仅当存在v使得 $R^{(k-1)}$中$r{iv}=1, r_{vj}=1$

Warshall(A[1..n, 1..n])
	// 计算传递闭包的Warshall算法
	// 输入：A[1..n, 1..n]包含n个顶点的有向图的邻接矩阵
	// 输出：A的传递闭包
	R^0 = A
	for i = 1 to n do
		for i = 1 to n do
			for j = 1 to n do
				if R^(k-1)[i, j] == 1 or
					(R^(k-1)[i, k] == 0 and R^(k-1)[k, j] == 0)
					R^k[i, j] = 1
	return R^n

算法特点

• 算法效率

  • 时间效率$\in \Theta(n^3)$
    • 重新构造最内层循环，可以提高对某些输入的处理速度
    • 将矩阵行视为位串，使用或运算也可以加速
  • 空间效率取决于如何处理布尔矩阵

• 蛮力法：所有点分别作为起点作一次搜索，记录能够访问的顶点

  • 对有向图遍历多次
  • 使用邻接链表表示稀疏图，蛮力法渐进效率好于Warshall算法

最小生成树

Prim算法

Prim算法：求解最小图最小生成树算法

• 每次添加距离当前树距离最近顶点进树
• 不断迭代构造最小生成树

算法

• 从图顶点集V中任选单顶点作为序列中初始子树

• 对图中顶点维护两个标记：树中最近顶点、相应距离

  • 与树不直接相连顶点置：NULL、$\infty$
  • 每次添加新节点更新两个标记
  • 可使用优先队列维护提高效率

• 以贪婪的方式扩张当前生成树，添加不在树中的最近顶点

• 更新顶点和树距离最近的顶点、相应距离

  • 只需考察与新添加顶点直接相连顶点即可

• 不断迭代直到所有点都在树中

Prim(G):
	// 构造最小生成树Prim算法
	// 输入：加权连通图G=<V, E>
	// 输出：E_T, 组成G最小生成树的边集合
	V_T = {v_0}
		// 使用任意顶点初始化树顶点集合
	E_T = NULL
		// 初始化生成树边为空集

	for i = 1 to |V|
		if i connect V_T
			connect_V[i] = 0
			connect_D[i] = e(0, i)
		else
			connect_V[i] = NULL
			connect_D[i] = \infty
	// 初始化节点和树最近节点列表、节点与树距离列表

	for i = 1 to |V|-1 do
		// 重复n-1次，直到树包含所有顶点
		edge = min(connect_D)
			// 寻找距离树最近的点
		v = vertex(edge)

		V_T = V_T union {v}
		E_T = E_T union {edge}

		connect_V[v] = NULL
		connect_D[v] = \infty
		更新和v相连的顶点两个标记值
	return E_T

算法特点

• 算法时间效率依赖实现优先队列、存储图数据结构

  • 图权重矩阵、优先队列无序数组$\in \Theta(|V|^2)$
  • 图邻接链表、二叉最小堆$\in O(|E|log|V|)$
  • 图邻接链表、Fibonacci Heap $\in O(|E| + |V|log|V|)$

• 对树进行扩展时用到的边的集合表示算法生成树

• 穷举查找构造生成树，生成树数量呈指数增长，且构造生成树 不容易

Kruskal算法

Kruskal算法：把最小生成树看作是具有$|V|-1$条边、且边权重最小 的无环子图，通过对子图不断扩展构造最小生成树

算法

• 按照权重非递减顺序对图中边排序

• 从空子图开始扫描有序列表，试图把列表中下条边加到当前子图 中，如果添加边导致回路则跳过

• 不断添加边直到达到$|V|-1$

Kruskal(G)
	// 构造最小生成树的Kruskal算法
	// 输入：G=<V, E>加权连通图
	// 输出：E_T，组成G的最小生成树边集
	reverse_sort([w(e_i)])
		// 按照边权非递减顺序对边集排序
	E_T = NULL
	ecounter = 0
	k = 0
	while ecounter < |V|-1 do
		k += 1
		if E_T union {e_k} 无回路
			// 常用并查算法检查`e_k`连接的两个顶点是否在
			// 同一棵树（并查集）中
			E_T = E_T union {e_k}
			ecounter += 1
	return  E_T

算法特点

• Kruskal每次迭代都需要检查添加新边是否会导致回路，其实 效率不一定比Prim算法高

• Kruskal算法中间阶段会生成一系列无环子图（树）

  • 子图不总是联通的
  • 可以看作是对包含给定图所有顶点、部分边的森林所作的 连续动作
  • 初始森林由|V|棵普通树构成，包含单独顶点
  • 最终森林为单棵树，包含图中所有顶点
  • 每次迭代从图的边有序列表中取出下条边，找到包含其端点 的树，若不是同一棵树，则加入边生成一棵更大的树

• 算法效率

  • 如果检查顶点是否位于同一棵树算法高效，则算法运行时间 取决于排序算法，时间效率$\in O(|E|log|E|)$

Sollin算法

Sollin算法：Prim算法、Kruskal算法的结合，将图每个顶点视为 子树，每次添加多条边合并子树直至得到最小生成树

算法

• 将图中每个顶点视为一棵树，整个图表示森林$F^{(0)}$
• 为森林$F$中每棵树选择最小代价边合并两棵树
• 重复以上，直至所有树合并为一棵树

Sollin(G):
	// 无向图最小生成树Sollin算法
	// 输入：无向图G
	// 输出：最小生成树边集
	MST_E = NULL
	Forest = G.V
	while |MST_E| < |G.V|:
		for tree in Forest:
			e = find_min(G.E)
			tree_b = get_tree(e)
			MET_E.add(e)
			tree.union(tree_b)

todo

算法特点

• 算法效率
  • 每轮子树数量减少一半，则最多重复log|V|轮算法终止
  • 时间效率$\in O(|E|log|V|)$

最短路径

Dijkstra算法

Dijkstra算法：求解单起点、权值非负最短路径算法

• 按照从给定起点到图中各顶点的距离，顺序求出离起始点 最近的顶点、相应最短路径

• 第i次迭代前，算法已经确定了i-1条连接起点、离起点前i-1近 顶点的最短路径

  • 这些构成了给定图的一棵子树$T_i$
  • 可以在同$T_i$顶点邻接的顶点中找到和起点最接近的顶点 （边权非负）

• 算法类似于Prim算法，两个对代价评价标准不同

  • Dijkstra算法是各条路径长度：有重复边，考虑整个路径
  • Prim算法是评价各边总和：无重复边，只考虑一条边

算法

• 对顶点维护两个标记：起点到该顶点最短路径长度d、路径上 前个顶点pre_v

  • 一般使用优先队列维护最短路径长度
  • 对所有顶点维护：$\infty$、NULL标记不在树中、不与树 邻接顶点
  • 仅对生成树中顶点、邻接顶点维护：每次迭代更新列表

• 根据标记选择邻接顶点中和起始点距离d最小顶点，添加进树

• 更新顶点标记

  • 因为生成树只新添加一个顶点，只需要考虑与新添加顶点 直接相连、未在树中顶点
  • 比较与起始点距离是否改变

• 不断迭代直至所有点均在树中

Dijkstra(G, s)
	// 单起点最短路径Dijkstra算法
	// 输入：G=<V, E>非负权重加权连通图，顶点s起始点
	// 输出：对V中每个顶点，从s到v的最短路径长度d_v
	Initialize(Q)
		// 将顶点优先队列初始化为空
	for v in V
		d_v = \infty
		p_v = NULL
		Insert(Q, s, d_s)
			// 初始化有限队列中顶点优先级
	d_s = 0
	Decrease(Q, s, d_s)
		// 更新s优先级为d_s
	V_T = NULL

	for i = 0 to |V|-1 do
		u* = DeleteMin(Q)
			// 删除优先级最小元素
		V_T = V_T \union {u*}
		for v in V-V_T 中与u*邻接顶点 do
			if d_u* + w(u*, u) < d_u
				d_u = d_u* + w(u*, u)
				p_u = u*
				Decrease(Q, u, d_u)

算法特点

• 算法时间效率同Prim算法

Bellman-Ford算法

Bellman-Ford算法：求解单节点、权值正负无限制最短距离

• 权值正负无限制意味着贪心策略不再有效
• 要求路径中不存在负权值回路
• 对n个顶点图，路径最长为n-1，否则删除回路路径长度不增加

算法

考虑使用动态规划算法

• 令$dist^{(l)}[u]$表示从起点v到节点u边数不超过l的最短 路径长度

  • 在不允许出现负权值回路的前提下，构造最短路算法过程 最多只需要考虑n-1条边

  • 即$dist^{(n-1)}$是从v到u不限制路径中边数目的最短路径 长度

Floyd算法

Floyd算法：求解完全最短路径问题，有向、无向、加权图均适用 （边距离不为负，否则距离可以任意小）

• 构造n+1个距离矩阵$D^{(k)}, k=0,1,\cdots,n$

  • $D^{(k)}$中元素$d_{ij}$表示顶点i、j之间由编号小于k的 顶点作为中间顶点的距离

  • $D^{(0)}$：初始权重矩阵

  • $D^{(k)}, 0<i<n$：路径中顶点编号最大为k

  • $D^{(n)}$：目标距离矩阵

  • 后继矩阵相对前趋，允许作为路径上顶点增加，各顶点间 距离可能缩短

• 考虑$D^{(k)}$通过直接前趋$D^{(k-1)}$计算得到，其中距离 （路径）分为两类

  • $d^{(k)}{ij} = d^{(k-1)}{ij}$：不包含顶点k作为中间 节点的路径

  • $d^{(k)}{ij} = d^{(k-1)}{ik} + d^{(k-1)}{kj} < d^{(k-1)}{ij}$： 包含顶点k作为中间节点的路径

算法

$$d^{(k)}_{ij} = \min \{ d^{(k-1)}_{ik} + d^{(k-1)}_{kj}, d^{(k-1)}_{ij}, d^{(k-1)}_{ij} \}$$

Floyd(W[1..n, 1..n])
	// 计算完全最短路径的Floyd算法
	// 输入：W不包含负距离的距离矩阵
	// 输出：包含最短距离的距离矩阵
	D^0 = W
	for k = 1 to n do
		for i = 1 to n do
			for j = 1 to n do
				D[i, j] = min(D[i, j], D[i, k] + D[k, j])
	return D

算法特点

• 算法效率

  • 时间效率同Warshall算法为立方级
  • 如上伪码的空间效率为平方级（没有创建n+1距离矩阵）

• Floyd算法类似于Warshall算法

• Floyd算法利用最优性原理，即最短路径中子路径也是最短

最大流量问题

Augmenting-Path Method

Shortest-Augmented-Path算法

最短增益路径法（first-labeled first-scanned algorithm）

• 对网络中顶点维护两个标记

  • 从源点到被标记顶点能增加流量数
  • 路径中前个顶点名称
    • +：从前向边访问到当前顶点
    • -：从后向边访问到当前顶点

• 对网络的每条边$(i, j)$，初始化流量为$x_{ij}=0$

• 从源点开始同时沿着前向边、后向边进行广度优先搜索

  • 先更新前向边
  • 只有有增益空间边（顶点）才能被访问
  • 更新搜索到顶点标记

• 源点被标记表明得到一条增量路径，沿着标记反向更新边流量

• 若广度优先搜索无法达到源点，表明不存在流量增益路径，当前 流量值作为最大值返回

ShortestAugmentingPath(G)
	// 最短增量路径算法
	// 输入：流量网络G
	// 输出：最大流量x
	对网络中每条边，设置x[i, j] = 0
	把源点标记为(\infty, -)，加入空队列Q中
		// 使用队列实现广度优先搜索
	while not Empty(Q) do
		i = Front(Q)
		Dequeue(Q)
		for 从i到j的每条边 do
			// 遍历从i出发的边，前向边
			if j未被标记
				r[i, j] = = u[i, j] - x[i, j]
				if r[i, j] > 0
					l[j] = min{l[i], r[i, j]}
					/// 更新从源点到顶点j能增加的流量数
					用l[j], i+标记j
					Enqueue(Q, j)
		for 从j到i的每条边 do
			// 遍历到达i的边，后向边
			if j未被标记
				if x[j, i] > 0
					l[j] = min{l[i], x[j, i]}
					// 更新源点到顶点j能增加的流量数
					用l[j], i-标记j
					Enqueue(Q, j)
		if 汇点被标记
			// 沿着找的增益路径进行增益
			j = n
			while j != 1
				// 反向更新到源点为止
				if 顶点j前个节点为i+
					// 通过前向边访问到顶点j
					x[i, j] = x[i, j] + l[n]
				else
					x[j, i] -= l[n]
				j = i
		去除除源点外所有顶点标记
		重新初始化化队列Q

算法特点

• 算法正确性可以（联合）最大流-最小割定理证明

• 算法时间效率

  • 可以证明最短增益路径算法用到的增益路径数量不超过 $|V||E|/2$
  • 对使用邻接列表表示的网络，用广度优先查找找到一条增益 路径的时间$\int O(|V|+|E|)$
  • 所有算法时间效率$\in O(|V||E|^2)$

• 迭代算法

Preflow推进算法

预流：满足容量约束，但是不满足流量守恒约束

• 把过剩流量向汇点处移动，直到网络所有中间顶点都满足流量 守恒约束为止

算法特点

• 算法时间效率
  • 这类算法中较快者最差效率可以接近$O(|V||E|)$

Dinitz算法

Karzanov算法

Malhotra-Kamar-Maheshweari算法

Goldberg-Tarjan算法

单纯形法

此问题仍然是线性规划问题，可以使用单纯形法等通用解法求解

最大匹配（二分图）

匈牙利算法

算法

• 对U中每个顶点维护一个标记：与其匹配的对偶顶点

• 从V中的一个自由顶点v出发，按广度优先搜索找到U中自由 顶点u，寻找增益路径，搜索过程中

  • V中顶点：按照广度优先搜索，得到不在匹配M中的边

    • 搜索到U中自由顶点，则停止得到增益路径
    • 搜索到U中被标记顶点，则连接上已有匹配

  • U中顶点：直接找到其在V中的对偶顶点，得到在M中边

• 得到一个增益路径，沿着增益路径回溯，奇数边加入匹配

• 未找到自由顶点时，则无法得到增益路径

MaximumBipartiteMatching(G)
	// 用类似广度优先算法遍历求二分图的一个最大匹配
	// 输入：二分图G=<V, U, E>
	// 输出：输入图中一个最大基数匹配
	初始边集合M包含某些合法的匹配（例如空集合）
	初始队列Q包含V的所有自由顶点（任意序）
	while not Empty(Q) do
		w = Front(Q)
		Dequeue(Q)
		if w \in V
			for 邻接w的每个顶点u do
				// 二分图性质保证u一定在U中
				if u是自由顶点
					// 增益
					M = M \union (w, u)
						// 首边进匹配
					v = w
					while v已经被标记 do
						// 从增益路径回溯生成匹配
						u = 以v标记的点
						M -= (v, u)
							// 偶数边出匹配
						v = 以u标记的点
						M += (v, u)
							// 奇数边进匹配
					删除所以顶点标记
					用V中所有自由顶点重新初始化Q
					break
						// 增益后，重新搜索
				else
					// u已经匹配
					if (w, u) not \in M and u未标记
						用w标记u
						Enqueue(Q, u)
		else
			// w \in U，此时w必然已经匹配
			用w标记w的对偶v
				// 将已有匹配添加进增益路径中
			Enqueue(Q, v)
	return M
		// 当前匹配已经是最大匹配

算法特点

• 注意：从自由顶点开始寻求匹配时，无论是否找到增益路径， 路径中中U中节点标记已经更新，匹配仅在得到增益路径才更新

• 算法时间效率

  • 每次迭代花费时间$\in O(|E|+|V|)$，迭代次数 $\in O(|V|/2 + 1)$
  • 若每个顶点的信息（自由、匹配、对偶）能在常数时间内 得到（如存储在数组中）
  • 则算法时间效率$\in O(|V|(|V| + |E|))$

• 算法正确性参见图graph_undirected关于增益路径-最大匹配

• 迭代算法

霍普克罗夫-卡普算法

算法特点

• 对匈牙利算法的改进，把多次迭代在一个阶段完成，然后用一次 查找把最大数量边添加到匹配中

• 算法时间效率：$\in O(\sqrt {|V|}(|V| + |E|))$

稳定婚姻问题

婚姻稳定算法

存在自由男士，任选求婚、回应之一执行，直至不存在自由男士

• 求婚：自由男士m向女士w求婚，w为其优先级最大、之前未拒绝 过其女士（可以是已匹配）

• 回应：若女士w自由则接受男士m求婚，与之配对；女士w不自由 则把m同当前配偶匹配，选择其中优先级较高者

算法

算法特点

• 算法会在$n^2$次迭代内终止：至多每位男士向所有女士求婚

• 性别倾向：总是生成man-optimal的稳定匹配，优先满足 男士偏好

  • 在任何稳定婚姻中，总是尽可能把优先级最高的女士分配给 男性
  • 使用女士进行求婚也只会把性别偏见反向，而不能消除

• 对给定的参与者优先选择集合而言，男士（女士）最优匹配唯一

  • 由性别性别倾向容易证明
  • 所以算法的输出不取决于自由男士（女士）求婚顺序，可以 使用任何数据结构表示参与者集合而不影响结果

• 算法最终输出匹配M为稳定婚姻匹配证明参见graph

分配问题（二分图）

n个任务分配给n个人执行（一人一个），将任务j分配个人i的成本为 $C_{ijd}$，求最小成本分配方案

• 类似问题：最大权重匹配问题

蛮力算法

算法

• 生成整数n的全部排列
• 根据成本矩阵计算每个分配方案总成本
• 选择和最小的方案

特点

• 算法排列次数为$n!$

分支界限法

• 第i层节点下界可取：$lb = c + \sum_{k=i+1}^n min{c_k}$

  • $c$：当前成本
  • $min{c_k}$：成本矩阵第k行最小值

算法

特点

匈牙利算法

算法

特点

Topological Sorting

拓扑排序：按照次序列出有向图的顶点，使得对图中每条边，其 起始顶点总在结束顶点之前

删点法

算法

• 在有向图中求出源（没有输出边的顶点），然后把删除其和所有 从它出发的边
• 不断重复，直到不存在源，如果此时图中还有顶点，则图中存在 环，无解
• 则删除节点顺序即为拓扑排序可行解

TopologicalSort(G):
	// 从有向图中不断删除入度为0的点、入栈，判断有向图G是否
		// 为DAG，并给出拓扑排序栈
	// 输入：有向图G
	// 输出：拓扑排序栈T
	InitStack(S)
	indgree = [v.indegree for v in G]
	for v in G:
		if v.indgree == 0
			S.push(v)
		// 存储0入度结点栈
	count = 0
		// 删除结点计数
	while(!S.empty())
		v = S.pop()
		T.push(v)
		count++
		for(u connected to v)
			if --indgree.u == 0
				S.push(u)
	if count < |G.V|
		// 结点未删除完毕，但无0入度结点
		// G中有回路，报错
		return ERROR
	return T

特点

• 算法效率
  • 时间效率$\in O(|V|+|E|)$
• 减常数法

DFS逆后序遍历

图中无环时，由某点出发进行DFS

• 最先退出DFS的为出度为0的点，即拓扑有序序列中最后顶点

• 按照DFS退出先后次序得到序列即为逆向拓扑有序序列

  • 使用逆后序方式存储DFS访问顶点，判断是否有环、出栈 次序即为正向拓扑有序序列

应用

• 判断庞大项目中相互关联任务不矛盾，然后才能合理安排，使得 项目整体完成时间最短（需要CPM、PERT算法支持）

Cirtical Path问题

找出使用AOE网表示的工程的中关键路径

• 关键路径由关键活动构成
• 即耗费时间变动对工程整体完成时间有影响的活动

拓扑排序求解

• 最早、最晚开始时间检查是否为关键活动
• 建立活动（边）、事件（顶点）发生事时间关系
• 拓扑排序求解事件发生最早、最晚时间

• 具体参见algorithm/data_structure/graphdi_specials

算法

TopologicalOrder(G):
	// 从有向图中不断删除入度为0的点、入栈，判断有向图G是否
		// 为DAG，并给出拓扑排序栈
	// 输入：有向图G
	// 输出：拓扑排序栈T、顶点事件最早发生事件ve
	InitStack(S)
	indgree = [v.indegree for v in G]
	ve[0..|G.V|] = 0
	for v in G:
		if v.indgree == 0
			S.push(v)
		// 存储0入度结点栈
	count = 0
		// 删除结点计数
	while(!S.empty())
		v = S.pop()
		T.push(v)
		count++
		for(u connected by v)
			ve[u] = max{ve[u], ve[v] + len(v, u)}
				// 若有更长路径，更新
			if --indgree[u] == 0
				S.push(u)
	if count < |G.V|
		// 结点未删除完毕，但无0入度结点
		// G中有回路，报错
		return ERROR
	return T, ve

CriticalPath(G, T, ve):
	// 逆序求顶点事件最晚发生时间，求出关键活动
	// 输入：有向无环图G，G拓扑排序
	// 输出：关键活动队列Q
	vl[0..|G.V|] = ve
	Q = InitQueue()
	while(!T.empty())
		v = T.pop()
		for (u connect to v)
			vl[u] = min{vl[u], vl[v] - len(u, v)}
	for(v in G.V)
		for (u connected by v)
			ee = ve[v]
			el = vl[u] - len(v)
			if(el == ee)
				Q.push(G.edge(v, u))
	return Q

• 以上算法中在生成拓扑排序栈时同时得到各顶点事件最早发生 时间

• 可以只获取拓扑排序栈，然后处理其获得顶点事件最早发生时间 ，将两个功能分离，只是处理一遍顶点而已

• 也可以使用其他算法获得拓扑排序栈

  • DFS遍历甚至可以遍历顶点一遍，同时获得顶点事件最早、 最晚发生时间

特点

• 算法效率
  • 时间效率$\in O(|V|+|E|)$

哈密顿回路问题

确定给定图中是否在包含一条哈密顿回路

回溯算法

算法

• 对所有节点维护标记：是否位于当前路径中

• 选择某节点a作为哈密顿回路起点顶点，即回溯状态空间树根

• 从根节点开始处理

  • 若节点周围还有未标记节点，选择下个加入路径、标记
  • 若节点周围没有未标记节点，回溯到之前节点重新处理

• 直到所有节点都被标记，且当前节点和根节点相邻

特点

旅商问题

Traveling Salesman Problem：对相互之间距离已知为正整数的n座 城市，求最短漫游路径，使得在回到出发城市之前，对每个城市只 访问一次

• 即：对权重为正整数的无向完全图寻找最短哈密顿回路

蛮力算法

算法

• 生成n-1个中间城市的组合得到所有旅行线路
• 计算线路长度，求得最短路径

特点

• 算法排序次数为$(n-1)!/2$

改进

• 线路成对出现，只是方向相反，可考虑任意两个相邻顶点，只 考虑包含其某个排序的线路

分支界限法

• 第i层下界可取$lb = \sum{k=i+1}^n d{k1}$

• 更紧密、也不复杂的下界 $lb = \lceil \frac {\sum{k=i+1}^n (d{k1} + d_{k2})} 2 \rceil$

  • $d{k1}, d{k2}$：城市$i+1$到最近的两个城市距离

  • 最短路径为两个端点共享，至多只能有一个端点能够成为 该边起点

  • 若要求所有哈密顿回路中必须包括某些边，则在考虑相应 边端点城市时，使用必须边（若不是节点最短边）替换其中 次短边

• 只需要生成某对节点有序的路径：可以消去状态空间树中部分 分支

算法

特点

旅商问题非精确算法

以下均是讨论TSP问题的欧几里得实例，不对称实例等已经证明更难 解决，对精确算法、启发式算法都是如此

贪婪算法

Nearest-Neighbor算法

• 任意选择城市开始
• 每次访问和当前城市k最接近的城市，直到访问完所有城市
• 回到开始城市

Multifregment-Heuristic算法

求给定加权完全图的最小权重边集合，且每个顶点连通度均为2

• 将边按权重升序排列，将要构造的旅途边集合开始时空集合

• 不断尝试将排序列表中下条边加入旅途边集合

  • 边加入不会使得某节点连通度大于2
  • 不会产生长度小于n的回路
  • 否则忽略这条边

• 返回旅途集合

算法特点

对属于欧几里得类型的旅商问题实例（大部分）

• 此时虽然两个算法的精确性能比无法界定，但是满足 $\frac {f(s_a)} {f(s^{*})} \leqslant \frac 1 2 (\lceil log_2 n \rceil + 1)$

Minimum-Spaning-Tree-Based Algorithm

基于最小生成树的算法

• 哈密顿回路中去掉一条边就能得到一棵生成树$T_h$
• 可以先构造一棵最小生成数$T^{*}$，然后在其基础上构造近似 最短路径

Twice-Around-The-Tree算法

• 对给定实例构造最小生成树$T^{}$（Prim, Kruskal*）
• 从任意顶点开始，（利用深度优先遍历）绕树散步一周，记录 经过顶点
• 扫描顶点列表，消去重复出现顶点（走捷径，直接去新城市）， 除列表尾部重复起点，得到一条哈密顿回路

• 可能是考虑到最小生成树能够选出部分最短路径？？？

特点

对属于欧几里得类型的旅商问题

• 绕树两周算法是2近似算法：$2f(s^{*}) > f(s_a)$

  • $f(s^{} > w(T_h) \geqslant w(T^{})$：最优哈密顿 回路去掉一条边后长度大于等于最小生成树长度
  • $f(s^{}) < 2w(T^{})$：第二次扫描走捷径距离小于绕树 一周距离
  • 这里限定了特点类型实例，并没有找到对所有旅商问题的 优先近似算法

Christofides算法

同样利用问题与最小生成树的出关系，但更复杂

算法

• 对给定实例构造最小生成树$T^{*}$
• 构造包含包含$T^{*}$的欧拉回路
  • 找出最小生成树中所有连通度为奇数的顶点
  • 求出这些顶点的最小权重匹配（匈牙利算法）
  • 将最小权重匹配边加入树中得到多重图欧拉回路
• 使用走捷径方法将欧拉回路转换为哈密顿回路

特点

对属于欧几里得类型的旅商问题

• 绕最小生成树一周得到的路径是多重图的一条欧拉回路，其中 多重图为将当前图每条边重复一遍得到

  • 绕树两周算法：直接原始欧拉回路上走捷径
  • Christofides算法：重新构建更短的欧拉回路，在此基础 上走捷径

• Christofides算法是1.5近似算法

  • 实际应用中，Christofides算法近似解明显好于绕树两周
  • 可以对连通度大于2顶点尝试不同访问次序，即将回路 中邻接顶点分别两两组合，找到访问其的最佳路径

迭代改进算法

Local Search Heuristics：本地查找启发法

• 这类算法从某个初始旅途（随机或简单近似算法生成）开始

• 每次迭代把当前旅途一些边用其他边代替，试图得到和当前旅途 稍有差别的旅途

  • 若能得到优于当前旅途的新旅途，则替换当前旅途，继续 寻找
  • 否则，返回当前旅途，停止

2选算法

删除旅途中2条非临边，把两条边端点用另一对边重新连接

• 此操作称为2改变
• 为保证重连后得到合法哈密顿回路，重连方法只有一种

3选算法

删除3条非临边后重连

• 重连方法有3种
• 事实上可以推广到k选，但是只有3改变被证明有意义

Lin-Kernighan算法

变选算法算法的一种

• 可以视为在3选操作后进行一系列2选操作

算法特点

• 迭代改进算法求得的近似解效果质量非常好
• Lin-Kernighan算法是公认的求解高质量近似解的最佳算法

Held-Karp Bound

Held-Karp下界

• 将TSP描述为线性规划问题求解（忽略整数约束）得到，计算 速度快
• 一般和最优旅途长度非常接近，误差不超过1%
• 可使用其代替最短旅途估计近似算法的精确度

模拟

• 10000个随机点：坐标、距离取整
• Comqaq ES40：500MHz的Alpha处理器、2GB内存

启发式算法	超过Held-Karp下界的%	运行时间
最近邻居	24.79	0.28
多片段	16.42	0.20
Christofides	9.81	1.04
2选	4.70	1.41
3选	2.88	1.50
Lin-Kernighan	2.00	2.06