图

分类

图$G=$：由一些称为顶点的点构成的集合，其中某些顶点由 称为边的线段相连

• 有限集合V：元素为顶点vertex
• 有限集合E：元素为顶点二元组，称为边edge/弧arc

边方向

Undigraph/Undirected Graph

• 无向图：所有边都是无向边的图
• 无向边：若有序对$(u, v) \in E$，必有$(v, u) \in E$， 即E是对称的，顶点对$(u, v)$等同于$(v, u)$，没有顺序

对无向边$(u, v)$

• 则顶点u、v相互adjcent
• 其通过undirected edge$(u, v)$相连接
• 顶点u、v称为边$(u, v)$的endpoint
• u、v和该边incident（相依附）

Digraph

• 有向图：所有边都是有向边的图
• 有向边：若有序对对$(u, v) \in E$无法得到$(v, u) \in E$， 即两者不等同，有顺序

对有向边$(u, v)$

• 边$(u, v)$的方向是从顶点u到顶点v
• u称为tail，v称为head

边权重

Ordered Graph

有序图：各边地位有序

Weighted Graph/Network

加权图/网络：给边赋值的图

• 值称为weight或cost
• 有大量的现实应用

边数量

• complete graph：任意两个顶点直接都有的边相连的图
  • 使用$K_{|v|}$表示有|V|个顶点的完全图
• dense graph：图中所缺的边数量相对较少
• sparse：图中边相对顶点数量较少

特点

• 不考虑loop（顶点连接自身边），则含有|V|个顶点无向图 包含边的数量|E|满足： $ 0 \leq |E| \leq \frac {|V|(|V| - 1)} {2} $

• 对于稀疏图、稠密图可能会影响图的表示方法，影响设计、使用 算法的运行时间

图表示方法（存储结构）

Adjacency Matrix

邻接矩阵：两个数组分别存储数据元素（顶点）信息、数据元素之间 关系（边）的信息

• n个顶点的图对应n * n的bool矩阵
  • 图中每个顶点使用一行和一列表示
  • i、j节点间有边，则矩阵第i行、j列元素为1，否则为0
• 无向图邻接矩阵一定是对称的，有向图邻接矩阵不一定

typedef enum{DG, DN< UDG, UDN} GraphKind;
typedef struct ArcCell{
	VRType adj;
		// 顶点关系类型：无权图0、1是否相邻，加权图权值类型
	InfoType * info;
		// 弧相关信息
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct{
	VertexType vexs[MAX_VERTEX_NUM];
		// 顶点向量
	AdjMatrix arcs;
	int vexnum, arcnum;
		// 图当前顶点弧数
	GraphKind kind;
}

Adjacency List

邻接表：n条单链表代替邻接矩阵的n行，对应图G的n个顶点

• 每个顶点用一个邻接表表示

  • 线性表的header表示对应的顶点
  • 链表中结点表示依附于顶点的边

• 无向图一条边在邻接链表中对应两条链，有向图对应一条

  • 有向图出度计算简单
  • 计算入度则比较复杂，如果需要频繁计算入度，可以再存储 一个反向邻接表

typedef struct ArcNode{
	int adjvex;
		// 弧指向顶点信息
	struct ArcNode *nextarc;
		// 指向下条弧指针
	InfoType * info;
		// 弧相关信息
}ArcNode;
typedef struct VNode{
	VertexType data;
		// 顶点信息
	ArcNode * firstarc;
		// 首条依附该顶点的弧指针
}VNode, AdjList[MAX_VERTEX_NUM];
typedef struct{
	AdjList vertices;
	int vexnum, arcnum;
	int kind;
}

Orthogonal List

十字链表：将有向图的邻接表、逆邻接表结合起来

• 有向图中每条弧、每个顶点对应一个结点
• 弧结点所在链表为非循环链表，
  • 结点之间相对位置自然形成，不一定按照顶点序号有序
• 表头结点即顶点结点，顺序存储

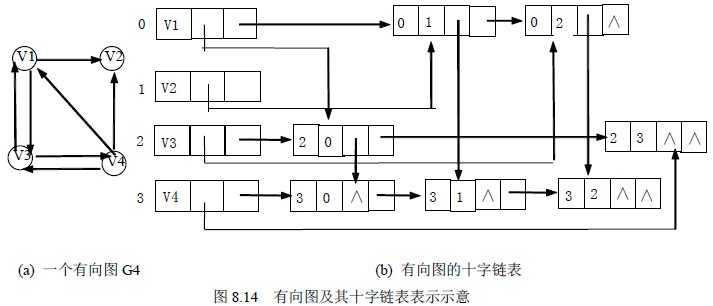
typedef struct ArcBox{
	int tailvex, headvex;
		// 头、尾顶点链域
	struct ArcBox *hlink, *tlink;
		// 头相同、尾相同弧链域
	InfoType *info;
		// 弧相关信息
}ArcBox;
typedef struct VexNode{
	VertexType data;
		// 顶点信息
	ArcBox *firstin, *firstout;
		// 顶点第一条出、入弧
}VexNode;
typedef struct{
	VexNode xlist[MAX_VERTEX _NUM];
		// 表头
	int vexnum, arcnum;
}OLGraph;

Adjacency Multilist

邻接多重表：无向图的另一种存储形式

• 一条边对应唯一结点
  • 所有依附于同一顶点的串联在同一链表中
  • 每个边界点同时链接在两个链表中
  • 避免无向图邻接表中一条边两次出现
• 类似十字链表，仅无需区分头尾结点

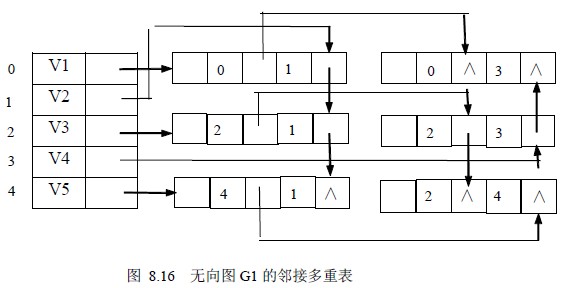
typedef struct EBox{
	VisitIf mark;
		// 访问标记
	int ivex, jvex;
		// 边依附的两个顶点
	struct EBox *ilink, *jlink;
		// 依附两个顶点的下条边
	InfoType *info;
		// 边信息指针
}EBox;
typedef struct VexBox{
	VertexType data;
	EBox *firstedge;
		// 第一条依附该顶点的边
}VexBox;
typedef struct{
	VexBox adjmulist[MAX_VERTEX_NUM];
	int vexnum, edgenum;
}AMLGraph;

说明

• 稀疏图：尽管链表指针会占用额外存储器，但是相对于邻接矩阵 占用空间依然较少

• 稠密图：邻接矩阵占用空间较少

• 邻接矩阵、邻接链表都可以方便的表示加权图

  • 邻接矩阵元素A[i, j]设置为有限值表示存在的边的权重， 设置为$\infty$表示不存在边，此时矩阵也称 weighted matrix或cost matrix
  • 邻接链表在节点中型跨同时包含节点名称和相应边权重

• 任何可以存储顶点、边的数据结构（如集合）都可以表示图， 只是存储效率低、无法高效操作

概念

路径

有向图

• directed path：有向图中顶点的一个序列，序列中每对连续 顶点都被边连接，边方向为一个顶点指向下一个顶点

• directed cycle：有向图中节点序列，起点、终点相同，每个 节点和其直接前趋之间，都有一条从前趋指向后继的边

• directed acyclic graph：DAG，有向无环图

无向图

• path：（无向）图G中始于u而止于v的邻接顶点序列，即为顶点u 到顶点v的路径

• simple path：路径上所有点互不相同

• cycle：特殊的path

  • 起点、终点都是同一顶点
  • 长度大于0
  • 不包含同一条边两次

• acyclic：不包含回路的图

长度

• length：路径中代表顶点序列中的顶点数目减1，等于路径中 包含的边数目
• distance：顶点间距离，顶点之间最短路径长度

连通性

无向图

• connected：顶点u、v连通，当且仅当存在u到v的路径

• connected graph：连通图，对图中的每对顶点$(u, v)$， 都有从u到v的路径

• connected component：连通分量，给定图的极大连通子图， 即没有可以添加的连通子图用于扩充

  • 非连通图中包含的几个自我连通的部分

• articulation point：关节点，如果从连通图$G$中删除顶点 $v$、极其邻接边各点之后的的图$G^{‘}$至少有两个连通分量， 则称顶点$v$为关节点

• biconnected graph：重连通图，没有关节点的连通图

• biconnected component：重连通分量，连通图的最大重连通 子图，即不是其他重连通分量的真子图

  • 两个重连通分量不可能共享一个以上节点，即图的一条边 不可能同时出现在两个重连通分量中 （否则两个“重连通分量”可以合并）
  • 所以可以说重连通分量是对原图的边的划分

有向图

• 强连通图：对所有不同顶点u、v，都存在u到v、v到u的路径
• strongly connected component：强连通分量，有向图的 极大连通子图

源点、汇点

• soruce：源，没有输入边的顶点
• sink：汇点，没有输出边顶点

图遍历

遍历图：实质是对每个顶点查找其邻接顶点的过程

• 具体算法参见algorithm/problem/graph

遍历方式

• BFS：Breadth First Search：广度优先搜索，类似树的先序 遍历

• DFS：Depth First Search：深度优先搜索，类似树的按层次 遍历

• 具体算法参见algorithm/problem/graph

结点处理顺序

• post-order：后序，先处理子节点，再处理当前结点
• pre-order：前序，先处理当前结点，再处理子节点

• 搜索森林中仅有一棵树时

  • 前序、后序均满足处理顺序（后序为逆处理顺序）
  • 前序、后序处理仅是处理顺序刚好相反

• 搜索森林中有多棵树时，将每棵树视为一个结点考虑

  • 每个树内前序、后序顶点处理顺序相反
  • 不同树整体前序、后序处理顺序相反
  • 此时前序不再满足处理顺序，后序仍为逆处理顺序，所以 前序不常用

• 节点处理记录方式

  • 栈：出栈顺序同记录反向
  • 队列：出队列顺序同记录顺序

总结

• Pre-Order：正前序，先当前顶点、后子顶点，队列存储

• Reverse Pre-Order：逆前序，先子顶点、后当前顶点， 栈存储

• Post-Order：正后序，先当前顶点、后子顶点，队列存储

• Reversed Post-Order：逆后序，先子顶点、后当前顶点， 栈存储，也称为伪拓扑排序

  • 可以用于得到DAG的拓扑有序序列
  • 也可以用于得到有环有向图的伪拓扑序列
    • 强连通分量整体看作结点，组成DAG
    • 各强连通分量必然可以选出某个顶点，满足在伪拓扑 序列中次序先于DAG中先驱强连通分量所有顶点
  • 用途最广
    • 有向图拓扑排序
    • Kosaraju算法中用到

BFS、DFS森林

广度优先、深度优先生成森林

• 遍历的初始顶点可以作为森林中树的根
• 遇到新未访问的顶点，将其附加为直接前趋子女
• 其实仅有树向边才是符合森林定义（其他边都只是搜索过程 中遇到）

• DFS森林中边是从左到右逐渐生成
• BFS森林中边是从上到下逐渐生成

边类型

• tree edge：树向边，连接父母、子女的边
• back edge：回边，连接非直接前驱的边
  • 对有向图包括连接父母的边
  • 对无向图不存在连接父母边
• cross edge：交叉边，连接非前驱、后继的边
• forward edge：前向边，连接非直接后代的边

边存在性

• 无向图
  • DFS森林：只可能有回边
  • BFS森林：只可能有交叉边
• 有向图
  • DFS森林：可以都有
  • BFS森林：只可能有回边、交叉边

Spanning Tree

生成树/极小连通子图：包含图中所有顶点的连通无环子图（树）

• n个顶点的生成树有且仅有n-1条边，反之不成立

• 在生成树添加一条边必定构成一个环，因为其实使得其依附的 两个顶点之间生成了第二条路径

Minimum Cost Spanning Tree

最小生成树：图的一棵权重最小的生成树（权重指所有边权重之和）

MST性质

• 若$N=(V, {E})$是连通网，U是顶点集V的非空子集，若 $(u, v), u \in U, v \in V-U$是一条具有最小权值（代价）边 ，则图中存在最小生成树包含该边

• 假设网N中最小生成树T不包含边$(u, v)$，将其加入T中

• 因为T为生成树，所以必存在边 $(u^{‘}, v^{‘}), u^{‘} \in U, v^{‘} \in V-U$，且 $u, u^{‘}$、$v, v^{‘}$之间均有路径连通

• 则删除$(u^{‘}, v^{‘})$可以消去上述回路，得到新生成树 $T^{‘}$，且代价不大于$T$，矛盾

• 存在是考虑到存在其他同权值边，若权值严格最小，则所有 最小生成树必然包含
• 依此性质生成算法参见algorithm/problems/graph

连通性

• 对图进行遍历是判断图连通性、求解连通分量的好方法

有向图

• 连通图：从图中任意顶点出发，进行深度、广度优先搜索即可 访问到图中所有顶点

  • 利用DFS生成树可以找出图的重连通分量

• 非连通图：需要从多个顶点起始进行搜索

  • 每次从新的起始点出发进行搜索过程中得到顶点访问 序列就是各个连通分量的顶点集

无向图

• 深度优先搜索是求有向图强连通分量的有效方法

• 具体算法参见algorithm/problem/graph