Tree

树&森林

Free tree

自由树：连通、无回路图，具有一些其他图不具有的重要 特性

• 边数总比顶点数少一：$|E|=|V|-1$

  • 这个是图为一棵树的必要条件，但不充分
  • 若图是连通的，则是充分条件

• 任意两个顶点之间总是存在简单路径

(Rooted)Tree

（有根）树：存在根节点的自由树

$$Tree = (root, F)$$

• $root$：根节点数据元素
• $F=(T_1, T_2, \cdots, T_m)$：森林
• $T_i=(r_i, F_i)$：根root的第i棵子树

• 在任意一棵非空树中

  • 有且仅有一个特定称为根的节点
  • 节点数n>1时，其余节点可以分为m个互不相交的有限集 ，每个集合本身又是一棵树，称为根的子树

• 树中任何两个节点间总存在简单路径，所以可以任选自由树 中某节点，作为有根树的根

• 有根树远远比自由树重要，所以也简称为树

  • 根一般放在树的顶层，第0层
  • 之后节点根据和根的距离放在相应层数

Forest

森林：无回路但不一定连通的图

• 其每个连通分量是一棵树
• 对树中每个节点，其子树集合即为森林

Ordered Tree

有序树：所有顶点的所有子女都是有序（不能交换次序）的有根树

应用

• 常用于描述层次关系

  • 文件目录
  • 企业的组织结构
  • 字典的实现
  • 超大型的数据集合的高效存储
  • 数据编码

• 用于分析递归算法

  • state-space tree：状态空间树，强调了两种算法设计 技术：回溯、分支界限

结构

• ancestor：从根到该顶点上的简单路径上的所有顶点
• proper ancestor：除自身外的所有祖先顶点
• parent：从根到顶点简单路径中，最后一条边的另一端节点
• parental：至少有一个子女的顶点
• child：
• sibling：具有相同父母的顶点
• leaf：没有子女的顶点
• descendent：所有以该顶点为祖先的顶点
• proper descendent：不包括顶点自身的子孙
• subtree：顶点的所有子孙、连接子孙的边构成以该顶点为根的 子树
• depth：根到该顶点的简单路径的长度
• height：根到叶节点的最长简单路径的长度

链式存储结构

• 链表结点代表树中一个顶点，其中至少包含：数据域、指向子女 的指针域
• 链表头指针指向二叉树根节点

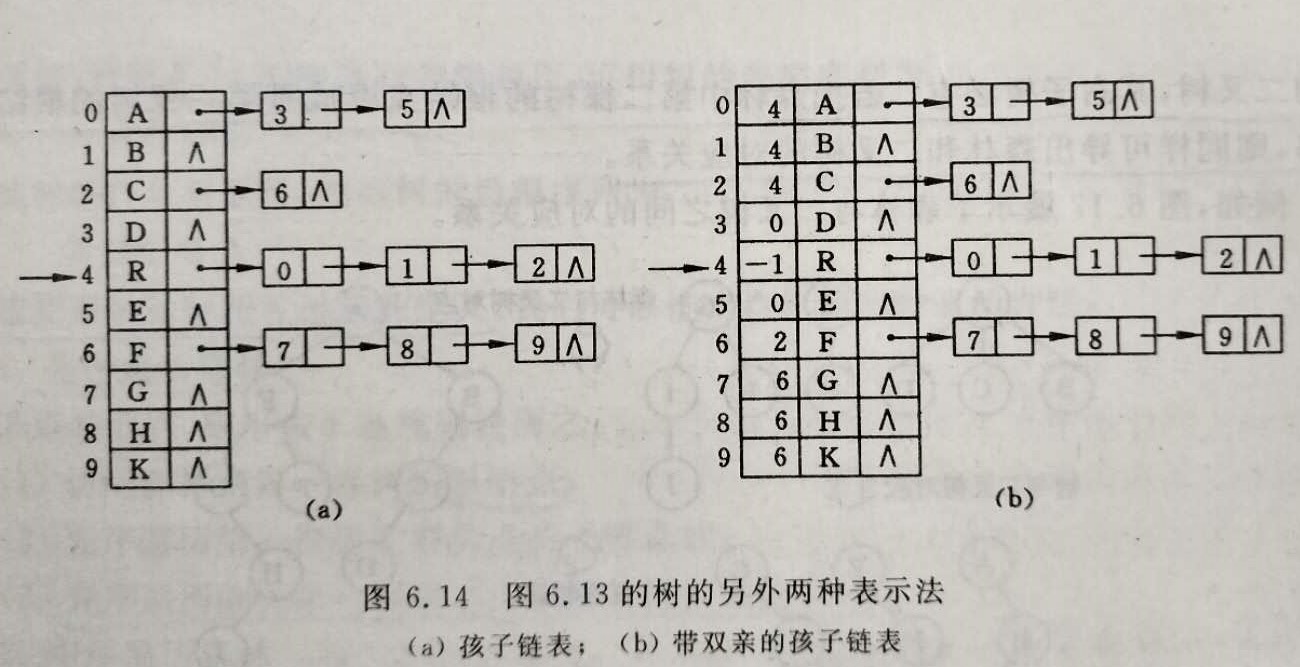
双亲表存储

双亲表示法

• 利用除根节点外，每个结点只有一个双亲，给所有结点添加一个 指向双亲的指针域

typedef struct PTNode{
	TElemType data;
	int parent;
}PTNode;
typedef struct{
	PTNode nodes[MAX_TREE_SIZE];
	int r, n;
}PTree;

• 求结点双亲时是常数时间
• 求结点孩子时需要遍历整个结构

孩子链表存储

孩子表示法

• 把每个结点的孩子结点排列起来，视为线性表，以单链表作为 存储结构

  • 否则结点同构则浪费空间，不同构时操作不方便

    

typedef struct CTNode{
	// 逻辑意义的结点，存储兄弟关系
	int child;
		// 结点位置，`nodes`中序号
	struct CTNode *next;
		// 指示下个兄弟结点
}*ChildPtr;
typedef struct{
	// 实际存储信息的结点
	TElemType data;
	ChildPtr firstchild;
		// 孩子链表头指针
}CTBox;
typedef struct{
	CTBox nodes[MAX_TREE_SIZE];
	int n, r;
		// 节点数，根节点位置
}CTree;

二叉链表存储

First Child-next Silbling Representaion：孩子兄弟/二叉链表 /二叉树表示法

• 每个节点只包含两个指针，左指针指向第一个子女，右指针指向 节点的下一个兄弟
• 节点的所有兄弟通过节点右指针被单独的链表连接

typedef struct CSNode{
	ElemType data;
	struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;

• 可高效的将有序树改造成一棵二叉树，称为关联二叉树
• 易于实现某些操作
  • 寻找孩子结点

森林与二叉树转换

• 给定一棵树，可以以二叉链表为媒介导出树与二叉树之间的对应 关系，即可以找到唯一一棵二叉树和与之对应

  • 任何一棵树对应的二叉树，其右子树必然为空

• 将森林中各棵树的根节点看作兄弟结点，则可以得到森林和 二叉树的对应关系

森林转换为二叉树

森林$F={T_1, T_2, \cdots, T_M}$转换为二叉树的 $B=(root, LB, RB)$

• 若F为空，即m=0，则B为空树
• 若F非空
  • root即为森林中第一个树的根$ROOT(T_1)$
  • LB是从$T_1$中根节点的子树森林转换而成的二叉树
  • RB是从森林$F^{‘}$转换而来的二叉树

二叉树转换为森林

二叉树的$B=(root, LB, RB)$转换为森林 $F={T_1, T_2, \cdots, T_M}$

• 若B为空，即m=0，则F为空树
• 若B非空
  • F中第一棵树根$ROOT(T_1)$即为二叉树根root
  • $T_1$中根节点的子树森林$F_1$是由B的左子树LB转换来的 子树森林
  • F中除$T_1$外的其余树组成的森林$F^{‘}$是由B的右子树 RB转换而来的子树森林

树、森林遍历

• 以二叉链表作树、森林的存储结构式，树、森林的先（根）序 遍历、后（根）序遍历对应二叉树先序、后序遍历

Binary Tree

二叉树：所有顶点子女个数不超过2个，每个子女不是父母的 left child就是right child的有序树

• 二叉树的根是另一棵二叉树顶点的左（右）子女
• 左右子树也是二叉树，所以二叉树可以递归定义
• 涉及二叉树的问题可以用递归算法解决

特点

• 二叉树第i层之多有$2^{i-1}$个节点
• 深度为k的二叉树最多有$2^k-1$节点

• 对任何二叉树$T$，如果其终端节点数$n_0$，度为2的节点数为 $n_2$，则$n_0=n_2+1$

  $$\left. \begin{array}{r} 考虑节点数：n = n_0 + n_1 + n_2 \\ 考虑分支数：n = n_1 + 2n_2 + 1 \end{array} \right \} \rightarrow n_0 = n_2 + 1$$

  • $n, n_0, n_1, n_2$：总结点数、终端节点数、度1节点数 、度2节点数

顺序存储结构

完全二叉树

顺序存储结构：顺序存储完全二叉树结点元素

typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree bt;

• 将完全二叉树编号为i的结点存储在一维数组中下标为i-1分量中
• 一般二叉树则将每个结点与完全二叉树结点相对照，存储在相应 分量中，并标记不存在的结点
  • 对某些二叉树空间利用效率极低
  • 所以顺序存储结构只适合完全二叉树

链式存储结构

• 二叉树的链表节点中至少包含3个域：数据域、左右指针域
• 链表头指针指向二叉树根节点
  • 为方便，也可以添加一个头结点，其lchild指针域指向 根结点

二叉链表

typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

• 含有n个结点的二叉链表中有n+1个空链域

三叉链表

typedef struct BiTriNode{
	TElemType data;
	struct BiTriNode *parent, *lchild, *rchild;
}BiTriNode, *BiTriTree;

• 在二叉链表基础上增加指向双亲结点的指针域

二叉线索链表

Threaded Binary Tree：线索二叉树/线索化树

• 使用二叉链表中的n+1个空链域存放二叉树遍历的前驱、后继 信息
• 附设标记域区分指针域存放子孙结点、前驱/后继

• 适合经常需要遍历的二叉树、查找遍历所得线性序列中前驱、 后继
  • 时间复杂度常数系数小
  • 无需设栈

typedef enum PointerTag{Link, Thread};
typedef struct BiThrNode{
	TElemType data;
	struct BitThrNode *lchild, *rchild;
	PointerTag LTag, RTag;
}BiThrNode, *BiThrTree;

• 后序线索化树找后继时需要知道双亲，应该使用带标志域的 三叉链表

Complete Binary Tree

• 满二叉树：深度为k且有$2^k-1$节点的二叉树，每层上的节点数 都是最大节点数

• 完全二叉树：essentially complete，树的每层都是满的，除 最后一层最右边的元素（一个或多个）可能有缺位

特点

• 只存在一棵n个节点完全二叉树，高度为 $\lfloor log_2 n \rfloor$

  • 深度为k、节点数为n的完全二叉树同深度为k的满二叉树中 1-n号节点一一对应
  • 叶子节点只可能在层次最大的两层上出现
  • 对任一节点，其左分支只能和右分支深度相同或大1

• 从上到下、从左到右对结点编号，即使用数组H存储完全二叉树 （从1开始编号，数组H[0]不存储节点值，或存放限位器）

  • 父母节点键会位于数组前$\lfloor n/2 \rfloor$个位置中 ，叶子节点位于后$\lceil n/2 \rceil$

  • 对位于父母位置i的键，其子女位于2i、2i+1，相应的对于 子女位置i的键，父母位于$\lfloor i/2 \rfloor$

应用

• 堆

二叉树高度

• 将空树高度定义为-1

算法

Height(T):
	// 递归计算二叉树的高度
	// 输入：二叉树T
	// 输出：T的高度
	if T = null_set
		return -1
	else
		return max{Height(T_left), Height(T_right)} + 1

特点

• 检查树是否为空是这个算法中最频繁的操作

• 算法时间效率

  • 树的节点数为n，则根据加法操作次数满足递推式 $A(n(T))=A(n(T{left})) + A(n(T{right})) + 1$， 得到$A(n(T)) = n$

  • 考虑为树中每个节点的空子树添加外部节点得到 扩展树，则外部节点数量x满足$x=n+1$

  • 检查树是否为空次数即为扩展树节点数目 $C(n(T))=n+x=2x+1$

二叉树遍历

• 不是所有关于二叉树的算法都需要遍历两棵子树，如：查找、 插入、删除只需要遍历两颗子树中的一棵，所以这些操作属于 减可变规模（减治法）

• 先序、中序、后序遍历都需要用到栈

• 中序遍历得到的序列称为中序置换/中序序列，先序、后序类似

递归版本

• Preorder Traversal：先序

  PreOrder(T):
  	visit(T)
  	if T_left not null:
  		PreOrder(T_left)
  	if T_right not null:
  		PreOrder(T_right)

• Inorder Traversal：中序

  InOrder(T):
  	if T_left not null:
  		InOrder(T_left)
  	visit(T)
  	if T_right not null:
  		InOrder(T_right)

• Postorder Traversal：后序

  PostOrder(T):
  	if T_left not null:
  		PostOrder(T_left)
  	visit(T)
  	if T_right not null:
  		PostOrder(T_right)

栈非递归

• 先序遍历

  • 深度优先入栈：左子树优先入栈

    • 节点先访问后入栈，栈内存已访问节点

    PreOrder(T):
    	s = InitStack()
    	cur = T
    	while s.not_empty() or cur:
    		while cur:
    			visit(cur)
    			s.push_back(cur)
    			cur = cur.left
    		cur = s.pop()
    		cur = cur.right
    
    // 等价写法，仅使用`if`利用外层循环
    PreOrder(T):
    	s = InitStack()
    	cur = T
    	while s.not_empty() or cur:
    		if cur:
    			visit(cur)
    			s.push_back(cur)
    			cur = cur.left
    		else:
    			cur = s.pop()
    			cur = cur.right

    • 基于对遍历性质的考虑
    • 扩展性较好，可以扩展到中序、后序遍历

  • 广度优先入栈：同层右、左节点先后入栈

    PreOrder(T):
    	s = InitStack()
    	s.push_back(T)
    	while s.not_empty():
    		cur = s.pop()
    		if cur.right:
    			s.push_back(cur.right)
    		if cur.left:
    			s.push_back(cur.left)
    		visit(cur)

• 中序遍历

  • 深度优先入栈

    • 节点先入栈后访问，栈内存未访问节点

    InOrder(T):
    	s = InitStack()
    	cur = T
    	while s.not_empty() or cur:
    		while cur:
    			s.push_back(cur)
    			cur = cur.left
    		cur = s.pop()
    		visit(cur)
    		cur = cur.right
    
    // 等价写法，仅使用`if`利用外层循环
    InOrder(T):
    	s = InitStack()
    	cur = T
    	while s.not_empty() or cur:
    		if cur:
    			s.push_back(cur)
    			cur = cur.left
    		else:
    			cur = s.pop()
    			visit(cur)
    			cur = cur.right

• 后序：需要标记当前节点左、右子树是否被访问

  • 深度优先入栈

    • 节点先入栈后访问，栈内存未访问节点
    • 记录最后一次访问节点，判断右子树是否被访问 （若右子树被访问，右子节点必然是上个被访问节点）

    PostOrder(T):
    	s = InitStack()
    	cur = T
    	last = NULL
    	while s.not_empty() or cur:
    		while cur:
    			s.push_back(cur)
    			cur = cur.left
    		cur = s.top()
    		// 检查右子树是否被访问过
    		if cur.right == NULL or cur.right == last:
    			visit(cur)
    			last = s.pop()	// 此时再弹出`cur`
    			cur = NULL		// 置`cur`为`NULL`，否则
    							// 再次访问左子树，死循环
    		else:
    			cur = cur.right

  • 或者为每个节点附设标志位

层次遍历

• 队列实现

  # 判断节点是否存在、再填充至队列
  LevelTraversal(T):
  	q = InitQueue()
  	cur = T
  	while q.not_empty() or cur:
  		if cur.left:
  			q.push_back(cur.left)
  		if cur.right:d
  			q.push_back(cur.right)
  		visit(cur)
  		cur = q.pop_first()
  
  # 先填充、再判断节点是否为`None`
  # 填充可保证、适合节点位置和满二叉树对应
  LevelTraversal(T):
  	q = InitQueue()
  	q.push(T)
  	# 层次遍历使用队列实现，所以无需像栈一样使用
  		# 两个判断条件`q.not_empty or cur`
  	while q.not_empty():
  		cur = q.pop_first()
  		# 弹出时判断节点是否有效
  		if cur:
  			visit(cur)
  			q.push_back(cur.left)
  			q.push_back(cur.right)

• 严格分层遍历：记录队列长度、遍历固定长度

  LevelTraversal(T):
  	q = InitQueue()
  	q.push(T)
  	while q.not_empty():
  		# 记录当前开始时队列长度
  		# 每轮遍历该长度数目元素，严格分层遍历节点
  		for i=0 to len(q):
  			cur_node = q.pop_left()
  			visit(cur_node)
  			if cur.left:
  				q.push_back(cur.left)
  			if cur.right:
  				q.push_back(cur.right)

树的计数

• 二叉树相似：二者为空树或二者均不为空树，且其左右子树分别 相似
• 二叉树等价：二者不仅相似，而且所有对应结点上的数据元素 均相同

• 二叉树的计数：n个结点、互不相似的二叉树数量$b_n$
• 树和一棵没有右子树的二叉树一一对应，所以具有n个结点不同 形态的树的数目，等于具有n-1个结点互不相似的二叉树数目

数学推导

二叉树可以看作是根节点、i个结点的左子树、n-i-1个结点的右子树 组成，所有有如下递推

$$\left \{ \begin{array}{l} b_0 & = 1 \\ b_n & = \sum_{i=0}^{n-1} b_i b_{n-i-1}, & n \geq 1 \end{array} \right.$$

求解得

$$b_n = \frac 1 {n+1} \frac {(2n)!} {n!n!} = \frac 1 {n+1} C_{2n}^n$$

遍历性质

• 给定结点的前序序列、中序序列，可以唯一确定一棵二叉树

• n个结点，不同形态二叉树数目恰是前序序列为$1 \cdots n$ 二叉树能得到的中序序列数目

• 中序遍历过程实质是结点进栈、出栈的过程，序列$1 \cdots n$ 按不同顺序进栈、出栈能得到排列的数目即为中序置换数目 $C{2n}^n - C{2n}^{n-1} = \frac 1 {n+1} C_{2n}^n$