总述

在给定的集合、多重集（允许多个元素具有相同的值）中找给定值 （查找键，search key）

• 顺序搜索
• 折半查找：效率高但应用受限
• 将原集合用另一种形式表示以方便查找

评价

没有任何一种查找算法在任何情况下都是最优的

• 有些算法速度快，但是需要较多存储空间
• 有些算法速度快，但是只适合有序数组

查找算法没有稳定性问题，但会发生其他问题

• 如果应用里的数据相对于查找次数频繁变化，查找问题必须结合 添加、删除一起考虑

• 必须仔细选择数据结构、算法，以便在各种操作的需求间达到 平衡

无序线性表查找

顺序查找

算法

• 将给定列表中连续元素和给定元素查找键进行比较
  • 直到遇到匹配元素：成功查找
  • 匹配之前遍历完整个列表：失败查找

1
2
3
4
5
6
7
8
9
10
11
12

SequentialSearch(A[0..n-1], K)
	// 顺序查找，使用**查找键作限位器**
	// 输入：n个元素数组A、查找键K
	// 输出：第一个值为K的元素位置，查找失败返回-1
	A[n] = K
	i = 0
	while A[i] != K do
		i = i + 1
	if i < n
		return i
	else
		return -1

改进

• 将查找键添加找列表末尾，查找一定会成功，循环时将不必每次 检查是否到列表末尾
• 如果给定数组有序：遇到等于（查找成功）、大于（查找失败） 查找键元素，算法即可停止

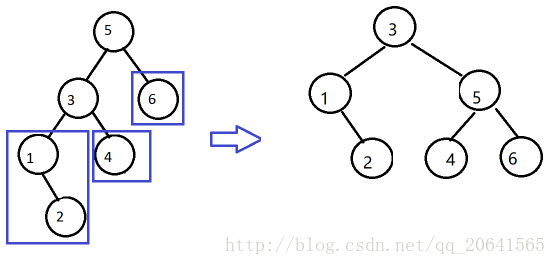
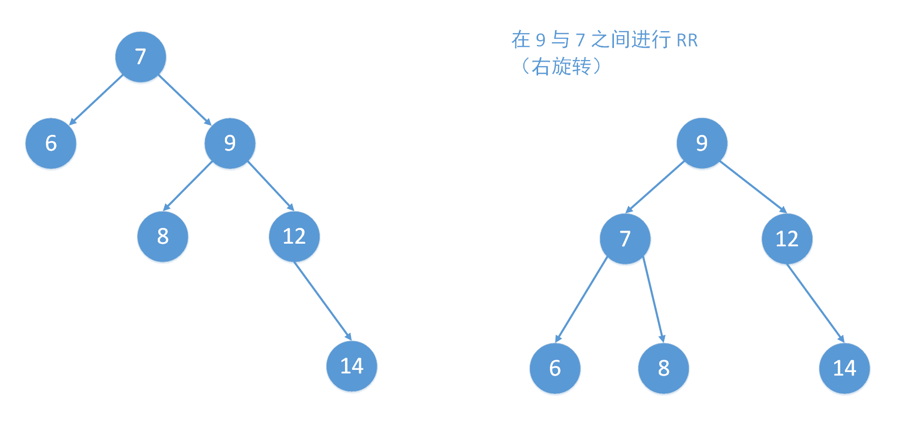
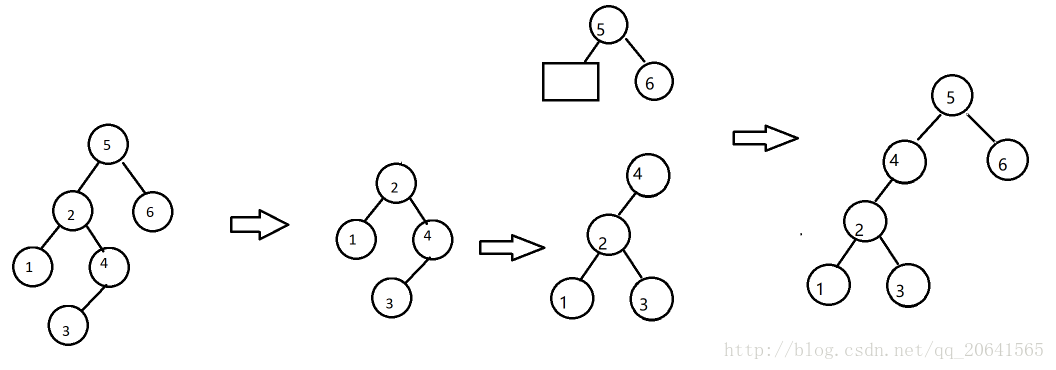
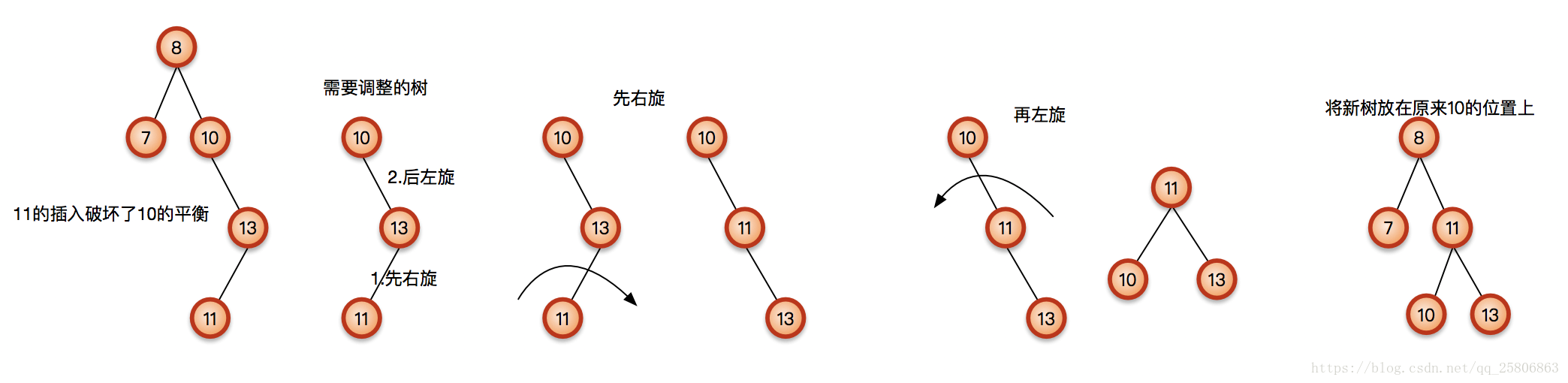
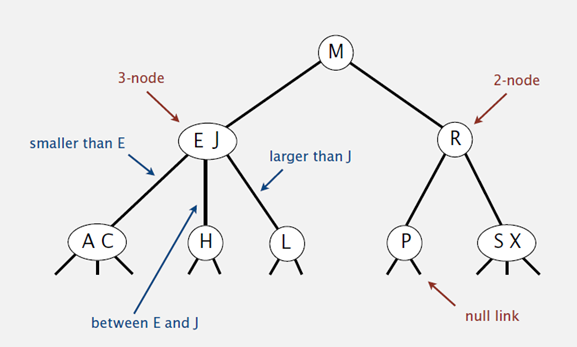
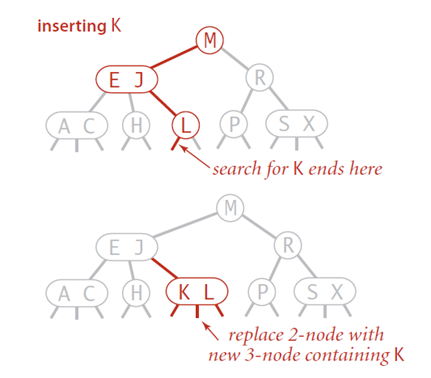
二叉查找树

算法

• 对数组构建二叉查找树
• 在二叉查找树上进行查找

特点

• 算法效率：参见二叉查找树

• 构建二叉查找树（插入）和查找操作基本相同，效率特性也相同

• 减可变规模 + 输入增强

预排序查找

对线性表预排序，有序表中查找速度快得多

算法

1
2
3
4
5
6
7

PreorderSearch(A[0..n-1])
	// 对数组预排序然后查找
	// 输入：可排序数组A[0..n-1]
	// 输出：元素在数组中的位置
	对B[(数组元素, 索引)]进行预排序
	使用折半查找寻找二元组
	返回二元组中索引

特点

• 算法时间效率：取决于排序算法

  • 查找算法在最差情况下总运行时间$\in \Theta(nlogn)$
  • 如果需要在统一列表上进行多次查找，预排序才值得

• 这种预排序思想可以用于众数、检验惟一性等， 此时算法执行时间都取决于排序算法 （优于蛮力法$\in \Theta(n^2)$）

• 变治法（输入增强）

预排序检验唯一性

1
2
3
4
5
6
7
8
9

PresortElementUniqueness(A[0..n-1])
	// 先对数组排序，求解元素唯一性问题
	// 输入：n个可排序元素构成数[0..n-1]
	// 输出：A中有相等元素，返回true，否则false
	对数组排序
	for i=0 to n-2 do
		if A[i] = A[i+1]
			return false
	return true

预排序求众数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

PresortMode(A[0..n-1])
	// 对数组预排序来计算其模式（众数）
	// 输入：可排序数组A[0..n-1]
	// 输出：数组模式
	对数组A排序
	i = 0
	modefrequency = 0
	while i <= n-1 do
		runlength = 1
		runvalue = A[i]
		while i + runlength <= n-1 and A[i+runlength] == runvalue
			// 相等数值邻接，只需要求出邻接次数最大即可
			runlength = runlength+1
		if runlength > modefrequency
			modefrequency = runlength
			modevalue = runvalue
		i = i+runlength

	return modevalue

有序顺序表查找

• 有序顺序表的查找关键是利用有序减规模

• 但关键不是有序，而是减规模，即使顺序表不是完全有序， 信息足够减规模即可

折半查找/二分查找

二分查找：利用数组的有序性，通过对查找区间中间元素进行判断， 缩小查找区间至一般大小

• 依赖数据结构，需能够快速找到中间元素，如数组、二叉搜索树

• 一般模板：比较中间元素和目标的大小关系、讨论

  1 2 3 4 5 6 7 8 9

  left, right = ... while condition(search_space is not NULL): mid = (left + right) // 2 if nums[mid] == target: // do something elif nums[mid] > target: // do something elif nums[mid] < target: // do somthing

  • 函数独立时，找到target可在循环内直接返回
  • 函数体嵌入其他部分时，为方便找到target应break， 此时涉及跳出循环时target可能存在的位置
    • 找到target中途break
    • 未找到target直到循环终止条件

基本版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

BinarySearchEndReturnV1(nums[0..n-1], target):
	// 非递归折半查找基本版，不直接返回，方便嵌入
	// 输入：升序数组nums[0..n-1]、查找键target
	// 输出：存在返回数组元素下标m，否则返回-1
	left, right = 0, n-1
	while left <= right:
		mid = (left + right) // 2
		if nums[mid] == target:
			break
		elif nums[mid] < target:
			left = mid+1
		else:
			right = mid-1
	else:
		assert(mid == right == left-1)

	# 仅最后返回，方便嵌入，下同
	if nums[mid] == target:
		return mid
	else:
		return -1

• 输入判断：无需判断输入列表是否为空

  • 终止条件保证不会进入，即不会越界

• 初始条件：left, right = 0, n-1

  • 左、右均未检查、需检查
  • 即代码中查找区间为闭区间$[left, right]$，此时 搜索区间非空

• 中点选择：mid = (left + right) // 2

  • 向下取整
  • 对此版本无影响，left、right总是移动，不会死循环

• 循环条件：left <= right

  • 搜索区间为闭区间，则相应检查条件为left <= right， 否则有元素未被检查
  • 在循环内left、right可能重合

• 更新方式：left=mid+1, right=mid-1

  • 为保证搜索区间始终为闭区间，需剔除mid

• 终止情况：right=left-1、mid=left/right

  • 循环条件、循环内部+1保证：上轮循环left==right
  • 越界终止情况：左、右指针均剔除mid，两侧均可能越界
    • mid=right=n-1, left=n
    • mid=left=0, right=-1

• target位置

  • 若存在target：必然在mid处，循环结束只需判断mid
  • 若不存在target
    • target位于[right, left]间
    • left=mid+1=right+1表示小于target元素数量

• 需要和左右邻居（查找结束后）、left、right比较 情况下，容易考虑失误，不适合扩展使用

高级版1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

BinarySearchV2(nums[0..n-1], target):
	left, right = 0, n
	while left < right:
		mid = (left + right) // 2
		if nums[mid] == target:
			break
		elif nums[mid] < target:
			left = mid+1
		else:
			right = mid
	else:
		assert(mid-1 == left == right)

	if nums[mid] == target:
		return mid
	else:
		return -1

• 输入判断：无需判断输入列表是否为空

  • 终止条件保证不会进入，即不会越界

• 初始条件：left, right = 0, n

  • 左未检查、需检查，右无需检查
  • 即代码中查找区间为左闭右开区间$[left, right)$

• 中点选择：mid = (left + right) // 2

  • 向下取整
  • 此处必须选择向下取整，否则left=right-1时进入死循环
  • 即：循环内检查所有元素，取整一侧指针必须移动

• 循环条件：left < right

  • 搜索区间为左闭右开区间，则检查条件为left < right， 此时搜索区间非空
  • 在循环内left、right不会重合

• 更新方式：left=mid+1, right=mid

  • 为保证搜索区间始终为左闭右开区间
    • 移动左指针时需剔除mid
    • 移动右指针时无需剔除mid

• 终止情况：right=left、mid=left/left-1

  • 循环条件、循环内部+1保证：上轮循环
    • left+1=mid=right-1
    • left=mid=right-1
  • 越界终止情况：仅左指针剔除mid，仅可能右侧越界
    • left=right=n=mid+1

• target位置

  • 若存在target：必然在mid处，循环结束只需判断mid
  • 若不存在target
    • left=mid=right：循环过程中target可能已不在 搜索区间中，最终位于(mid-1, mid)
    • mid+1=left=right：(mid, left)
    • left表示小于target元素数量

高级版2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

BainarySearchEndReturnV3(nums[0..n-1], target):
	// 折半查找，保持左右指针顺序、不重合
	// 输入：升序数组nums、查找键target
	// 输出：存在返回数组元素下标m，否则返回-1
	left, right = -1, n
	while left < right:
		mid = (left + right + 1) // 2
		if nums[mid] == target:
			break
		elif nums[mid] < target:
			right = mid-1
		else:
			left = mid

	if nums[mid] == target:
		return mid
	else:
		return -1

• 输入判断：无需判断输入列表是否为空

  • 终止条件保证不会进入，即不会越界

• 初始条件：left, right = -1, n-1

  • 左无需检查，右未检查、需检查
  • 即代码中查找区间为左开右闭区间$(left, right]$

• 中点选择：mid = (left + right + 1) // 2

  • 向上取整
  • 此处必须选择向上取整，否则left=right-1时进入死循环 （或放宽循环条件，添加尾判断）
  • 即：循环内检查所有元素，取整一侧指针必须移动

• 循环条件：left < right

  • 搜索区间为左开右闭区间，则检查条件为left < right， 此时搜索区间非空
  • 在循环内left、right不会重合

• 更新方式：left=mid, right=mid+1

  • 为保证搜索区间始终为左闭右开区间
    • 移动右指针时需剔除mid
    • 移动左指针时无需剔除mid

• 终止情况：left=right、mid=left/left+1

  • 循环条件、循环内部+1保证：上轮循环
    • left+1=mid=right-1
    • left+1=mid=right
  • 越界终止情况：仅右指针剔除mid，仅可能左侧越界
    • left=right=-1=mid-1

• target位置

  • 若存在target：必然在mid处，循环结束只需判断mid
  • 若不存在target
    • left=mid=right：循环过程中target可能已不在 搜索区间中，最终位于(right, right+1)
    • mid+1=left=right：(left, right)
    • left+1表示小于target元素数量

高级版3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

BinarySearchEndReturnV2(nums[0..n-1], target):
	// 折半查找，保持左右指针顺序、不重合
	// 输入：升序数组nums、查找键target
	// 输出：存在返回数组元素下标m，否则返回-1
	left, right = -1, n
	while left < right-1:
		mid = (left + right) // 2
		if nums[mid] == target:
			break
		elif nums[mid] < target:
			left = mid
		else:
			right = mid

	if nums[mid] == target:
		return mid
	else:
		return -1

• 输入判断：无需判断输入列表是否为空

  • 终止条件保证不会进入，即不会越界

• 初始条件：left, right = -1, n

  • 左、右均无需检查
  • 即代码中查找区间为开区间$(left, right)$

• 中点选择：mid = (left + right) // 2

  • 向下取整、向上取整均可

• 循环条件：left < right-1

  • 搜索区间为左开右闭区间，则检查条件为left < right-1， 此时搜索区间非空
  • 在循环内left、right不会重合

• 更新方式：left=mid, right=mid

  • 循环终止条件足够宽泛，不会死循环

• 终止情况：left=right-1、mid=right/right-1

  • 循环条件、循环内部+1保证：上轮循环
    • left+1=mid=right-1
  • 越界终止情况：左右初始条件均越界，则左、右均可能越界
    • mid=left=n-1、right=n
    • left=-1、mid=right=0

• target位置

  • 若存在target：必然在mid处，循环结束只需判断mid
  • 若不存在target
    • target始终在搜索区间(left, right)内
    • 最终位于(left, right)

高级版1-原

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

BinarySearchKeep1(nums[0..n-1], target):
	// 折半查找，保持左右指针顺序、不重合
	// 输入：升序数组nums、查找键target
	// 输出：存在返回数组元素下标m，否则返回-1
	if n == 0:
		return -1

	left, right = 0, n-1

	while left < right - 1:
		mid = floor((left + right) / 2)
		if nums[mid] == target:
			return mid

		elif nums[mid] < target:
			right = mid
		else:
			left = mid

	// post-procesing
	if nums[left] == target:
		return left
	if nums[right] == target:
		return right

	return -1

• 初始条件：left = 0, right = n-1
• 终止情况：left = right - 1
• 指针移动：left = mid, right= mid

• 关键特点

  • n>1时left、mid、right循环内不会重合
  • mid可以left、right任意比较，无需顾忌重合
  • 需要和左右邻居、left、right比较时适合使用
  • 扩展使用需要进行真后处理，对left、right进行判断

• 终止情况：left = right - 1

  • 循环过程中会保证查找空间至少有3个元素，剩下两个 元素时，循环终止
  • 循环终止后，left、right不会越界，可以直接检查

• target位置

  • 若存在target，可能位于mid、left、right

    • mid：因为找到nums[mid]==target跳出
    • left：left=0，循环中未检查
    • right：right=n-1，循环中未检查

  • 不存在target，则target位于(left, right)之间

  • 适合访问目标在数组中索引、极其左右邻居

• 仅仅二分查找的话，后处理其实不能算是真正的后处理

  • nums[mid]都会被检查，普通left、right肯定不会 是target所在的位置

  • 真正处理的情况：target在端点

    • left=0, right=1终止循环，left=0未检查
    • left=n-2, right=n-1终止循环，right=n-1未检查

  • 即这个处理是可以放在循环之前进行处理

高级版2-原

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

BinarySearchKeep0(nums[0..n-1], target):
	// 折半查找，保证左右指针不交错
	// 输入：升序数组nums、查找键target
	// 输出：存在返回数组元素下标m，否则返回-1
	if n == 0:
		return -1

	left, right = 0, n
	while left < right:
		mid = floor((left + right) / 2)
		if nums[mid] == target:
			return mid

		elif nums[mid] < target:
			left = mid + 1
		else:
			right = mid

	// post-processing
	if left != len(nums) and nums[left] == target:
		return left

	return -1

• 初始条件：left = 0, right = n，保证n-1可以被正确处理
• 终止情况：left = right
• 指针移动：left = mid + 1, right = mid
• 中点选择对此有影响，指针移动行为非对称，取ceiling则 终止情况还有left = right + 1

• 关键特点

  • left、right循环内不会重合
  • 由于floor的特性，mid可以right任意比较，无需 顾忌和right重合
  • 需要和右邻居、right比较时适合使用

• 终止情况：left = right

  • 循环过程中会保证查找空间至少有2个元素，否则循环 终止
  • 循环终止条件导致退出循环时，可能left=right=n越界

• target位置

  • 若存在target，可能位于mid、left=right
  • 若不存在target，则target位于(left-1, left)
  • 适合访问目标在数组中索引、及其直接右邻居

• 仅二分查找，甚至无需后处理

• 判断nums长度在某些语言中也可以省略

高级版3-原

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

BinarySearchNoKeep(nums[0..n-1], target):
	// 折半查找，保证左右指针不交错
	// 输入：升序数组nums、查找键target
	// 输出：存在返回数组元素下标m，否则返回-1
	if n == 0:
		return -1

	left, right = -1, n-1
	while left < right - 1:
		mid = floor((left + right) / 2)
		if nums[mid] == target:
			return mid

		elif nums[mid] < target:
			left = mid
		else:
			right = mid - 1

	// post-processing
	if right >= 0 and nums[right] == target:
		return right

	return -1

• 初始条件：left = -1, right = n-1
• 终止情况：left = right、left = right + 1
• 指针移动：left = mid, right = mid - 1
• 中点选择对此有影响，指针移动行为非对称，取ceiling则 同高级版本2

• 终止条件：left = right、left = right - 1

  • 循环过程中保证查找空间至少有3个元素，否则循环 终止

  • 由于floor特性，必须在left < right - 1时即终止 循环，否则可能死循环

  • 循环终止后，left=right=-1可能越界

• target位置

  • 若存在target，可能位于mid、left=right
  • 若不存在target，则target位于(left, left+1)
  • 适合访问目标在数组中索引、及其直接左邻居

• 此版本仅想实现二分查找必须后处理

  • 终止条件的原因，最后一次right=left + 1时未被检查 即退出循环

  • 可能在任何位置发生，不是端点问题

特点

• 前两个版本比较常用，最后两个版本逻辑类似

• 折半查找时间效率

  • 最坏情况下：$\in \Theta(log n)$
  • 平均情况下仅比最差稍好

• 就依赖键值比较的查找算法而言，折半查找已经是最优算法 ，但是插值算法、散列法等具有更优平均效率

• 减常因子因子法

插值查找

Interpolation Search：查找有序数组，在折半查找的基础上考虑 查找键的值

算法

• 假设数组值是线性递增，即数字值~索引为一条直线，则根据 直线方程，可以估计查找键K在A[l..r]所在的位置

  $$x = l + \left \lfloor \frac {(K-A[l])(r-l)} {A[r] - A[l]} \right \rfloor$$

• 若k == A[x]，则算法停止，否则类似折半查找得到规模更小的 问题

特点

• 即使数组值不是线性递增，也不会影响算法正确性，只是每次 估计查找键位置不够准确，影响算法效率

• 统计考虑

  • 折半插值类似于非参方法，只考虑秩（索引）方向
  • 插值查找类似参数方法，构建了秩（索引）和数组值模型， 但是线性关系基于假设
  • 如果模型错误可能会比折半查找效率更差，即在数据分布 分布偏差较大的情况下非参方法好于参数方法

• 所以是否可以考虑取样方法，先取5个点构建模型，然后估计

• 算法效率

  • 对随机列表，算法比较次数小于$log_2log_n+1$
  • 最差情况，比较次数为线性，没有折半查找稳定
  • Robert Sedgewick的Algorithms中研究表明，对较小文件 折半查找更好，大文件、比较开销大插值查找更好

• 减可变规模

子串匹配

蛮力字符串匹配

算法

• 将pattern对齐文本前m个字符，从左向右匹配相应字符
  • m个字符全部匹配，匹配成功，算法停止
  • 遇到不匹配字符则
• 模式右移1位，然后从模式首个字符开始重复以上匹配
• 在n-m位置无法匹配成功，则无足够匹配字符，算法停止

1
2
3
4
5
6
7
8
9
10
11
12

BruteForceStringMatch(T[0..n-1], P[0..m-1])
	// 蛮力字符串匹配
	// 输入：文本T：n个字符的字符数组
	//       模式：m个字符的字符数组
	// 输出：查找成功返回文本第一个匹配子串中第一个字符位置
	for i = 0 to m-m do
		j = 0
		while j < m and P[j] = T[i+j] do
			j = j + 1
			if j = m
				return i
	return -1

特点

• 最坏情况下，算法比较次数属于$O(nm)$
  • 即在移动模式之前，算法需要做足m次比较
  • 但是一般在自然语言中，算法平均效率比最差好得多
  • 在随机文本中，有线性效率

Horspool算法

算法从右往左匹配，在任意位置匹配不成功时只考虑 同模式最后字符匹配的文本字符c，确定安全移动距离，在 不会错过匹配子串的情况下移动最长距离

• 如果c在模式中出现，则模式移动到其最后c至同文本中c 匹配
• 否则移动模式长度m
• 特别的，如果c只在模式最后字符出现，则也应该移动m

算法

• 对给定长度m的模式及文本中用到的字母表，构造移动表t
• 将模式同文本开始对齐
• 重复以下过程直至发了了匹配子串或模式达到了文本字符外
  • 从模式最后字符开始，比较模式、文本相应字符
  • 若m个字符匹配，停止
  • 遇到不匹配字符c，若为当前文本中和模式最后匹配字符 对齐的字符，将模式移动t(c)个字符

1
2
3
4
5
6
7
8
9
10
11

ShiftTable(P[0..m-1])
	// 用Horspool算法、Boyer-Moore算法填充移动表
	// 输入：模式P[0..m-1]、可能出现字符表
	// 输出：以字符表为为索引的数组Table[0..size-1]
	for i=0 to size-1 do
		Table[i] = m
		// 初始化所有字符对应移动距离为m
	for j=0 to m-2 do
		Table[P[j]] = m - 1 - j
		// 对模式中存在的字符重新计算移动距离
	return Table

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

HorspoolMatching(P[0..m-1], T[0..n-1])
	// 实现Horspool字符串匹配算法
	// 输入：模式P[0..m-1]、文本T[0..n-1]
	// 输出：第一个匹配子串最左端字符下标，未匹配返回-1
	Table = ShiftTable(P[0..m-1])
	i = m - 1
	while i <= n-1 do
		k = 0
		while k <= m-1 and P[m-1-k]=T[i-k] do
			k = k+1
		if k == m
			return i-m+1
		else
			i = i+Table[T[i]]
	return -1

特点

• 算法效率

  • 最差情况下模式为相同字符，效率$\in O(nm)$
  • 对随机文本效率$\in O(n)$

• 输入增强

Boyer-Moore算法

• 坏符号移动：模式、文本中相应不匹配字符确定的移动 （不是Horspool中简单根据最后字符确定移动）
• 好后缀移动：模式、文本匹配的后缀确定的移动

算法

• 对给定长度m的模式及文本用到的字母表，构造坏符号移动表t
• 对给定长度m的模式构造后缀移动表
• 将模式与文本开始处对齐
• 重复以下直到找到匹配子串或模式达到文本字符以外
  • 从模式最后字符开始比较模式、文本相应字符
  • 所有m个字符匹配，则停止
  • 若c是不匹配字符，移动坏符号表、后缀移动表决定的 距离较大者

1
2
3
4
5

BadSymbolShift(P[0..m-1])
	// 创建坏符号移动表
	// 输入：模式P[0..m-1]
	// 输出：坏符号移动表

特点

• 算法效率

  • 算法效率最差也是线性的

• 输入增强

KMP算法

算法从左往右匹配，失败时不回溯指针，利用已经得到的 部分匹配结果尽可能将模式滑动一段距离，从模式中间next 字符开始比较

算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

KMPShift(P[0..m-1])
	// 计算KMP算法next值
	// 输入：模式P[0..m-1]
	// 输出：模式中各元素next值数组
	i = -1
		// 表示开始比较文本中下个字符
	j = 0
	next[0] = -1
		// 即如果模式首字符都不匹配，比较文本下个字符
	while j < m
		if i == -1 or P[j] == P[i]
			i += 1
			j += 1
			// 当前字符匹配成功，决定下个字符next值
			next[j] = i
		else
			i = next[i]
			// 若当前字符没有匹配成功，不会立即处理下个字符
			// next值，而是反复迭代、查询已匹配部分next值，
			// 以获得最大匹配前缀
	return next

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

KMPShiftVal(P[0..m-1])
	// 计算KMP算法next值修正版（考虑next值与当前相等）
	// 输入：模式P[0..m-1]
	// 输出：模式中各元素next_val值数组u
	i = -1
		// 表示开始比较文本中下个字符
	j = 0
	next_val[0] = -1
	while j < m do
		if i == -1 or P[j] == P[i]
			i += 1
			j += 1
			if T[j] != T[i]
				next_val[j] = i
			else
				next_val[j] = next_val[i]
				// 考虑了next值相同时，可以再滑动一次
				// 这里会导致next_val值跳跃
		else
			i = next_val[i]
	return next_val

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

KMPMatching(P[0..m-1], T[0..n-1])
	// 实现KMP字符串匹配算法
	// 输入：模式P[0..m-1]、文本T[0..n-1]
	// 输出：第一个匹配子串最左端字符下标，未匹配返回-1
	i = 0
	j = 0
	while i < m and j < n do
		if i == -1 or P[i] == T[j]
			i += 1
			j += 1
		else
			i = next[i]
	if i >= m
		return j - m + 1
	else
		return -1

特点

• 算法效率

  • 算法时间效率$\in O(m+n)$

• 文本指针不需要回溯，整个匹配过程只需要对文本扫描一次， 对流程处理十分有效，可以边读边匹配

• 输入增强

禁忌搜索

总述

• 二叉查找树：最基础的查找树，但是不平衡时效率很差
• 自平衡查找树：使用旋转技术得到平衡二叉树
• 多路查找树：使用多叉树达到平衡

• 树高度一般即决定其查找、插入、删除效率
• 以代码复杂性、插入节点时间代价，换取查询时$logN$性能

Self-Balancing Binary Tree

自平衡查找树：如果节点插入、删除产生了一棵违背平衡要求的树， 就从称为旋转的一系列特定变换中选择一种，重新构造树使得 树满足平衡要求

• 不同的对平衡的定义产生了不同的实现
• 这种方案属于变治法中实例化简

Balance Factor

平衡因子：节点左、右子树高度差（一般右树-左数）

• AVL树中平衡情况下节点平衡因子只能为-1、+1、0

• 更新节点后可能存在不平衡节点，其平衡因子可能变为-2、+2

• 平衡因子也可以被定义为左右子树叶子数

Rotation

旋转需要使得二叉树平衡时，保证二叉树依然有序

• 左旋：节点平衡因子符号为正，即右子树高于左子树

  • 节点T下沉为其右儿子R的左儿子
  • 如果右儿子R本身有左子树RL，则左子树RL成为节点T 新右子树

• 右旋：节点平衡因子符号为负，即左子树高于右子树，

  • 节点T下沉为其左儿子L的右儿子
  • 如果左儿子L本身有右子树LR，则右子树LR成为节点T 新左子树

• 旋转只涉参与选择的至多3个节点指针变化，其余节点状态保持
• “旋转”行为确实类似：节点绕其子节点旋转，子节点旋转后上浮 成为父节点
• 参与旋转的两个节点也称为轴

分类

• AVL树
• 红黑树
• 分裂树

Multiway Search Tree

多路查找树：允许查找树中单个节点中不止包含一个元素

• 二叉查找树的推广，用于磁盘超大数据集的高效存取
• 此方案属于变治法中改变表现

分类

• 2-3树
• 2-4树
• B树
• B+树

Binary Search Tree

二叉查找树：分配给每个父母顶点的数字都比其左子树中数字大， 比右子树数字小

• 二叉树有序，保证二叉树能够快速找到中间元素，从而支持 二分查找

特点

• 对于n个顶点的二叉树，满足 $ \lfloor {log_{2}^{n}} \rfloor \leq h \leq n-1 $

• 二叉查找树的查找算法效率取决于二叉树的高度

  • 平均情况下，查找、插入、删除时间$\in Theta(logn)$

  • 最差情况下（严重不平衡的树，接近链表结构），树高度 h接近节点数n，查找、插入、删除时间$\in Theta(n)$

• 包含n个键的二叉查找树总数量 $c(n) = \frac 1 {n+1} C_{2n}^n, c(0)=1$

应用

• 查找

操作

查找

在给定二叉查找树中查找给定键值K

• 如果树为空，查找失败

• 若树不为空，将查找键K和树根节点K(r)比较

  • 相等则查找停止
  • $K < K(r)$：在左子树中继续查找
  • $K > K(r)$：在右子树中继续查找

特点

• 算法时间效率
  • 最差情况下，二叉树完全偏斜，需要进行n次比较
  • 随机情况下，查找n个随机键构造的二叉树比较次数$2logn$

插入

除非是空树，否则总是把新键K插入叶子节点中

• 通过查找K确定合适插入位置（叶子节点）
• 若K大于叶子节点键值，则作为右子女，否则作为左子女

最优二叉查找树

对集合中元素确定的查找概率，成功查找的平均比较次数最小的 二叉查找树（可以扩展到包含不成功查找）

• $a_i, i=1,2,\cdots,n$：从小到大互不相等的键
• $p_i, i=1,2,\cdots,n$：键查找概率
• $T_i^j$：由键$a_i, \cdots, a_j$构成的二叉树
• $C(i, j)$：成功查找的最小平均查找次数

动态规划构造

• 根据最优化法则，最优二叉查找树左右子树均是最优排列的

• 二叉树$Ti^j$有序，设树根为$a_1$，$a_2,..,a{k-1}$构成 的左子树、$a_{k+1},..,a_j$构成右子树均是最优排列的

递推式如下

• $1 \leqslant i \leqslant j \leqslant n$

  $$\begin{align} C(i, j) & = \min_{i \leqslant k \leqslant j} \{p_k + \sum_{s=i}^{k-1} p_s * (a_s在T_i^{k-1}中层数 + 1) + \sum_{s=k+1}^j p_s * (a_s在T_{k+1}^j中层数 + 1) \}\\ & = \min_{i \leqslant k \leqslant j} \{ \sum_{s=i}^{k-1} p_s * a_s在T_i^{k-1}中层数 + \sum_{s=k+1}^j p_s * a_s在T_{k+1}^j中层数 + \sum_{s=i}^j p_s \} \\ & = \min_{i \leqslant k \leqslant j} \{C(i, k-1) + C(k+1, j)\} + \sum_{s=i}^j p_s \end{align}$$

• $1 \leqslant i \leqslant n+1, C(i, i-1)=0$：空树

• $1 \leqslant i \leqslant n, C(i, i)=p_i$：单节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

OptimalBST(P[1..n])
	// 动态规划法构建最优二叉查找树
	// 输入：P[1..n]n个键查找概率
	// 输出：在最优BST中查找成功的平均比较次数，最优BST子树根表
	for i = 1 to n do
		C[i, i-1] = 0
		C[i, i] = P[i]
		R[i, i] = i
	C[n+1, n] = 0
		// 初始化平均查找次数表、子树根表
	for d = 1 to n-1 do
		// d为二叉树节点数
		for i = 1 to n-d do
			// n-d是为了控制j的取值
			j = i + d
			minval = \infty
			for k = i to j do
				// 遍历设置二叉树根节点
				if C[i, k-1] + C[k+1, j] < minval
					minval = C[i, k-1] + C[k+1, j]
					kmin = k
			R[i, j] = kmin
			sum = P[i]
			for s=i+1 to j do
				sum += P[s]
			C[i, j] = minval + sum
	return C[1, n], R

算法特点

• 算法效率
  • 算法时间效率为立方级
  • 算法空间效率为平方级

AVL Tree

AVL树：要求其节点在左右子树高度差不能超过1的平衡二叉树

• 基本思想：总能通过一次简单的节点重排使树达到平衡

  • 如果树插入操作使得一棵AVL树失去平衡，利用旋转对树作 变换
  • 若有多个这样的节点，找出最靠近新插入的叶子节点不平衡 结点，然后旋转以该节点为根的子树

• AVL树高度h即为其查找、插入效率

  • 包含n个节点AVL树高度h满足 $\lfloor log_2 n \rfloor \leq h < 1.4405log_2(n+2) - 1.3277$

  • 最差情况下，操作效率$\in \Theta(logn)$

  • 平均而言，在n不是太小时，高度h平均为 $1.01log_2 n + 0.1$（几乎同折半查找有序数组）

• AVL树缺点（平衡代价），阻碍AVL树成为实现字典的标准结构

  • 需要频繁旋转
  • 维护树的节点平衡
  • 总体比较复杂

旋转

按照节点平衡符号进行旋转：+左旋、-右旋

• 单旋：不平衡节点、不平衡子节点不平衡因子符号相同

  • 全为+：不平衡节点左旋
  • 全为-：不平衡节点右旋

• 双旋：不平衡节点、不平衡子节点不平衡因子符号不同

  • 先旋转不平衡子节点
  • 再旋转不平衡节点

• 优先考虑最底层、不平衡节点

插入节点

AVL树插入关键：查找不平衡节点

• 节点中应有存储其平衡因子的实例变量
• 插入过程中经过每个节点返回当前节点子树深度是否变化
• 比较节点平衡因子、子节点深度变化返回值判断是否平衡

• 插入过程中查询的每个节点都有可能不平衡
• 自下而上返回深度变化情况，优先旋转最底层不平衡节点

4种插入情况

根据插入情况的不同，对最靠近新插入叶子节点的不平衡点T

LL

插入T左儿子L的左子树LL：平衡因子全-

• 即T到最底层叶节点（只可能有一个）的路径为LL（中间省略）
• R-rotation：右单转，对T做一次右旋即可平衡

RR

插入T右儿子R的右子树R：平衡因子全+

• 即T到最底层叶节点（只可能有一个）的路径为RR（中间省略）
• L-rotation：左单转，对T做一次左旋即可平衡

LR

插入T左儿子L的右子树R：平衡因子-+

• 即T到最底层叶节点（只可能有一个）的路径为LR（中间省略）
• LR-rotation：左右双转
  • 先对左儿子L做一次左旋，变成LL模式
  • 在LL模式下，再对T做一次右旋

RL

插入T右儿子R的左子树L：平衡因子+-

• 即T到最底层叶节点（只可能有一个）的路径为RL（中间省略）
• RL-rotation：右左双转
  • 先对右儿子R做一次右旋，变成RR模式
  • 在RR模式下，再对T做一次左旋

实现

删除节点

• 在AVL树中删除键相对而言比较困难，但也是对数级的

实现

Red-Black Tree

红黑树：能够容忍同一节点的一棵子树高度是另一棵的2倍

Splay Tree

分裂树：

2-3树

2-3树：可以包含两种类型的节点2节点、3节点，树的所有叶子节点 必须位于同一层

• 2-3树的高度即决定其查找、插入、删除效率

  • 节点数为n的2-3数高度h满足 $log_3(n+1)-1 \leq h \leq log_2(n+1) - 1$
  • 最差、平均情况下，操作效率$\in \Theta(logn)$

• 2-3树总是高度平衡

  • 所有叶子节点位于同一层，即树根到其路径长度相同
  • 2-3树平衡代价
    • 树中节点可以有1或2个键，需要处理2种节点类型
    • 拆分3节点的情况有很多种

• 节点类型

  • 2节点：只包含1个键K、2个子女

    • 左子女：作为所有键都小于K的子树的根
    • 右子女：作为所有键都大于K的子树的根

  • 3节点：两个有序键$K_1 < K_2$、3个子女

    • 最左边子女：作为键值小于$K_1$的子树的根
    • 中间子女：作为键值位于$[K_1, K_2]$之间子树的根
    • 最右边子女：作为键值大于$K_2$的子树的根

• 类似的还有2-4树

查找

• 如果根是2节点，当作二叉树查找

  • 若K等于根键值，停止
  • 若K小、大于根键值，在左、右子树中查找

• 若根是3节点

  • 和两个键值比较，有相等，停止
  • 否则能确定应该在3棵子树中哪棵继续查找

插入节点

除非是空树，否则总是把新键K插入叶子节点中

• 查找K确定合适的插入位置（叶子节点）

• 若叶子节点2节点，根据大小关系将K作为第一个键或第二个键 插入

• 若叶子节点3节点，把叶子分裂为两个节点：3个键中最小的放入 第一个叶子中，最大的放入第二个叶子中，中间的键提升到原 叶子节点父母中

  

  • 若叶子就是根，则需要创建新根容纳中间键
  • 中间键的提升可能会导致父母节点分裂，并引起祖先链条上 多个节点的分裂

删除节点

B树

B树：允许节点可以有$1~m-1$个键（$2~m$个子女）

1
2
3
4
5
6
7

#define BTREE_M
typedef struct BTNode{
	unsigned int degree;				// 节点实际包含键数
	KeyType key_slots[BTREE_M-1];		// 节点存储键数组
	struct BTNode ptr_slots[BTREE_M];	// 指向子女节点指针
	struct BTNode * ptr_parent;			// 父节点指针
}BTNode, *BTNodePtr;

• $m$：B树阶数，节点允许最大子女数

  • 节点最多允许有$m-1$个条目
  • $m=2$即为二叉树、$m=3$即为2-3树

• 键：用于构建树的关键字，和具体条目类似于键值对

• 根节点具有$2~m$个子女，除非为叶子节点

• 非根、非叶节点具有$[\lceil m/2 \rceil, m]$个子女

  • 即具有$[\lceil m/2 \rceil - 1, m]$个有序键

  • 其中子树$T_0$所有键小于$K_1$，子树$T_1$中所有键大于 等于$K_1$小于 $K_2$，以此类推

• B树是完美平衡的：所有叶子节点在同一层上

查找

算法

• 输入：B树、目标查找键
• 输出：查找键所属B树节点（若存在）

• 从根节点开始，比较查找键k和节点中键序列大小

  • 节点中键有序，若B树阶数足够大，可考虑折半查找

• 若在节点键序列中找到匹配键，则查找成功、返回

• 否则根据比较结果选择合适分支，顺着指针链前进，在相应子女 节点中进行查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

BTreeSearch(T, k):
	// 在B树中搜索键
	// 输入：B树根节点T、目标查找键k
	// 输出：目标键所在节点、目标键在节点中序号
	i = 0
	cur = T

	// 遍历寻找目标键对应键、分支
	while i < cur.degree and k > cur.key_slots[i]:
		i += 1

	if i < cur.degree and k == cur.key_slots[i]:
		return cur, i
	elif cur.is_leaf():			// 未找到目标键
		return cur, -1
	else:
		return BTreeSearch(cur.ptr_slots[i], k)

分裂

算法

• 输入：待分裂节点父节点、待分裂节点序号

• 计算待分裂节点分裂中心

  • 将分裂中心右侧数据移动至新节点

• 将节点分裂中心、新节点提升至父节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

BTreeNodeSplit(T, ptr_idx):
	// 分裂B树中节点
	// 输入：待分裂节点父节点`T`、待分裂节点序号`ptr_idx`

	nnode = BTreeNode()
	fnode = T.ptr_slots[ptr_idx]

	// 分裂中心
	mid = fnode.degree // 2

	// 复制右半部分键至新节点
	nnode.key_slots[:fnode.degree - mid] = fnode.key_slots[mid:fnode.degree]
	fnode.key_slots[mid:fnode.degree] = NULL

	// 若原节点非叶子节点，复制右半部分指针至新节点
	if not fnode.is_leaf():
		nnode.ptr_slots[:fnode.degree + 1 - mid] = fnode.ptr_slots[mid: fnode.degree + 1]
		fnode.ptr_slots[mid: fnode.degree+1] = NULL

	// 修改两节点度
	nnode.degree = fnode.degree - mid
	fnode.degree = mid

	// 将分裂中心提升至父节点
	// 修改父节点指向子女节点指针
	T.key_slots.insert(fnode.key_slots[mid], ptr_idx)
	T.ptr_slots.insert(nnode, ptr_idx+1)	// 原节点指针不变

插入

• 输入：B树根T、待插入键K
• 假设B树中不存在键K，否则查找、更新对应值即可

• 根据需要插入键K，查找需要插入的叶子节点L
• 若叶子节点L键数小于m-1，直接插入结束
• 否则以叶子节点键值中位数mid为中心分裂
  • 将mid插入叶子节点L父节点P中
  • 将mid左子支指向分裂后左子树、右子支指向分裂后右子树
• 对父节点尝试操作

1
2
3
4
5
6
7
8
9
10
11
12
13

BTreeInsert(T, k)
	// 向B树中插入不存在键K
	// 输入：B树根T、待插入键k

	// 找到键`k`应该插入的叶子节点`L`
	L, _ = BTreeSearch(T, k)
	L.key_slots.insert_in_order(k)


	// 若节点已满、须分裂
	while L.is_full():
		BTreeNodeSplit(L.parent_ptr, L.get_index())
		L = L.parent_ptr

• 此实现是考虑节点都有空位容纳新键，节点插入新键后再 判断是否需要分裂

删除#todo

应用

• 类似一般查找树，把数据记录插入初始为空的树中构造B树

B+树

B+树：B树的一种变形树

• 其中非叶节点只有索引作用，跟记录相关信息均存放在 叶结点中
• B+树中所有叶结点构成有序链表，可以按照键次序遍历

查找

算法

• 从根开始，比较查找键K和节点中键大小，选择合适指针，顺着 指针链前进

• 指针链指向可能包含查找键的叶子节点，在其中查找K

  • 父母节点、叶子节点都是有序的，如果B树次数足够 大，可以考虑使用折半查找

算法效率

以B树作索引存储大型数据文件为例

• 查找指定查找键访问B树节点数量为B树高度$h+1$ （即磁盘访问次数）

• 次数为m、高度为h的B树能够包含最少节点数为 $n \geqslant 4 \lceiling m/2 \rceiling ^ {h-1} -1$， 即$h \leqslant \lfloor log_{[m/2]} \frac {n+1} 4 \rfloor + 1$

• 所以在B树中查找，访问磁盘次数$\in O(logn)$

  • 实际应用中，磁盘访问次数很少超过3，因为B树的根、甚至 是第一层节点会存储在内存中减少磁盘访问次数

插入

算法

• 查找新记录键K对应的叶子节点

• 若叶子节点中还有空间存放此记录，在保持键有序的情况下插入

• 若节点中没有空间

  • 将节点分裂，后半部分记录放在新节点中
  • 新节点中最小键$K^{‘}$、指向其的指针插入原叶子节点 父母节点中（原叶子节点键、指针之后）
  • 插入过程可以一直回溯到树根，甚至直到树根分裂

其他考虑

• 查找新记录对应叶子节点时就分裂满节点，可以避免递归分裂
• 将满叶子节点中部分键移动给兄弟节点，同时替换父母节点中的 键值（保证B树特点），增加少许复杂度以节约空间

算法特点

• 算法效率
  • 算法时间效率$\in O(logn)$

应用

• B+树是存储结构化记录数据集合最重要的索引结构
  • 所有数据记录（键）按照升序存储在叶子节点中，其父母 节点作为索引
  • B+树中节点常常对应磁盘中页
  • 考虑到访问磁盘页面是比较内存中键值比较时间多好几个 数量级，磁盘访问次数是衡量B树效率的主要指标

标