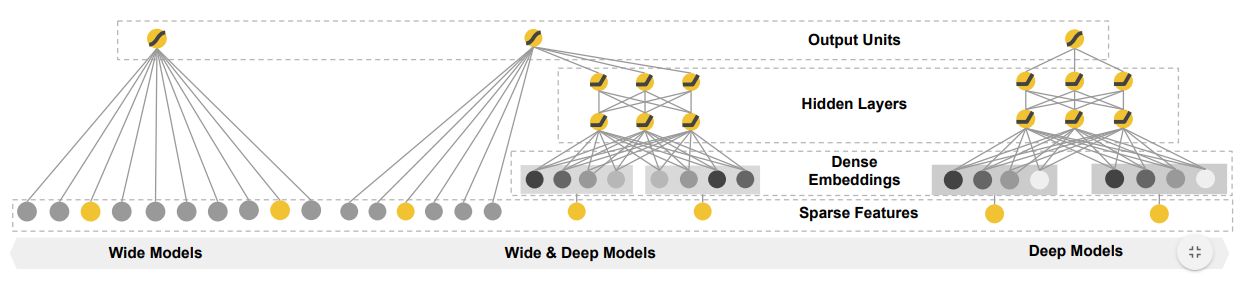
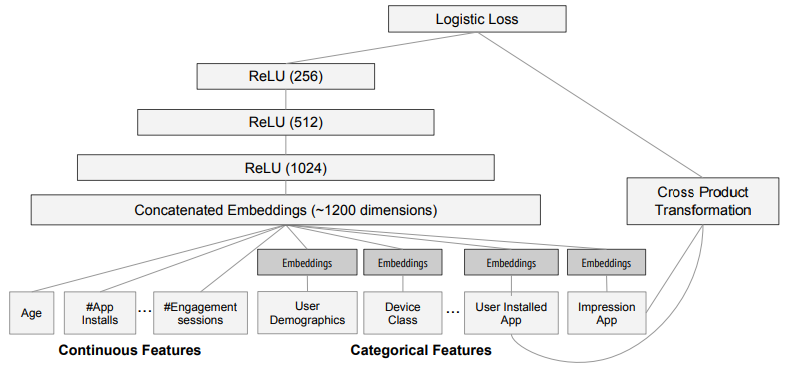
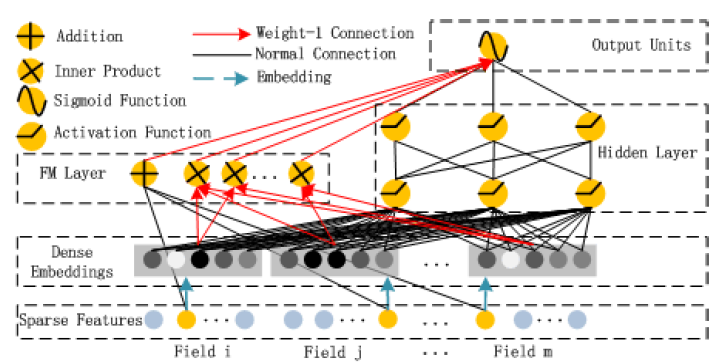
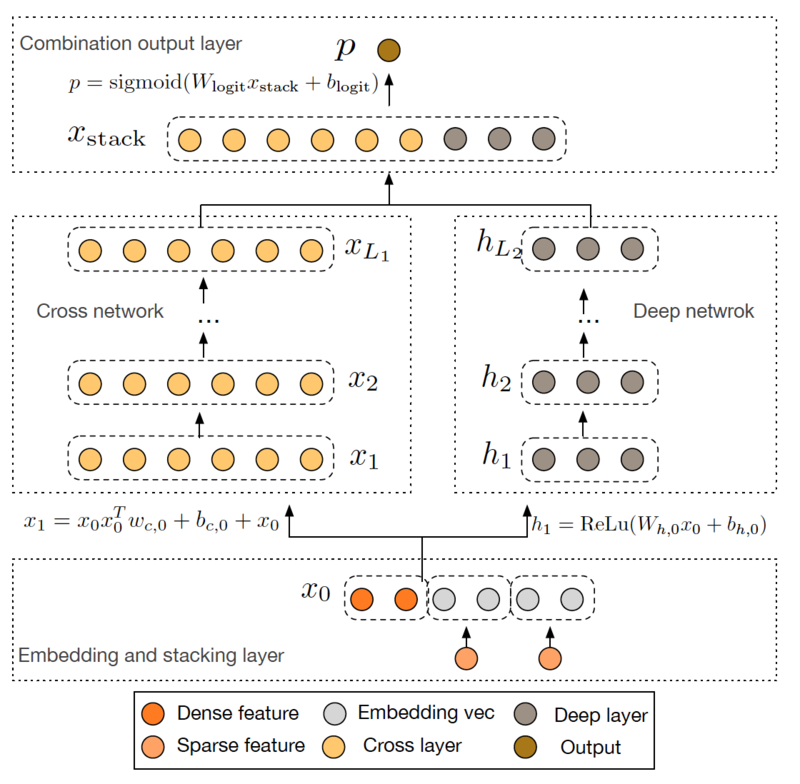
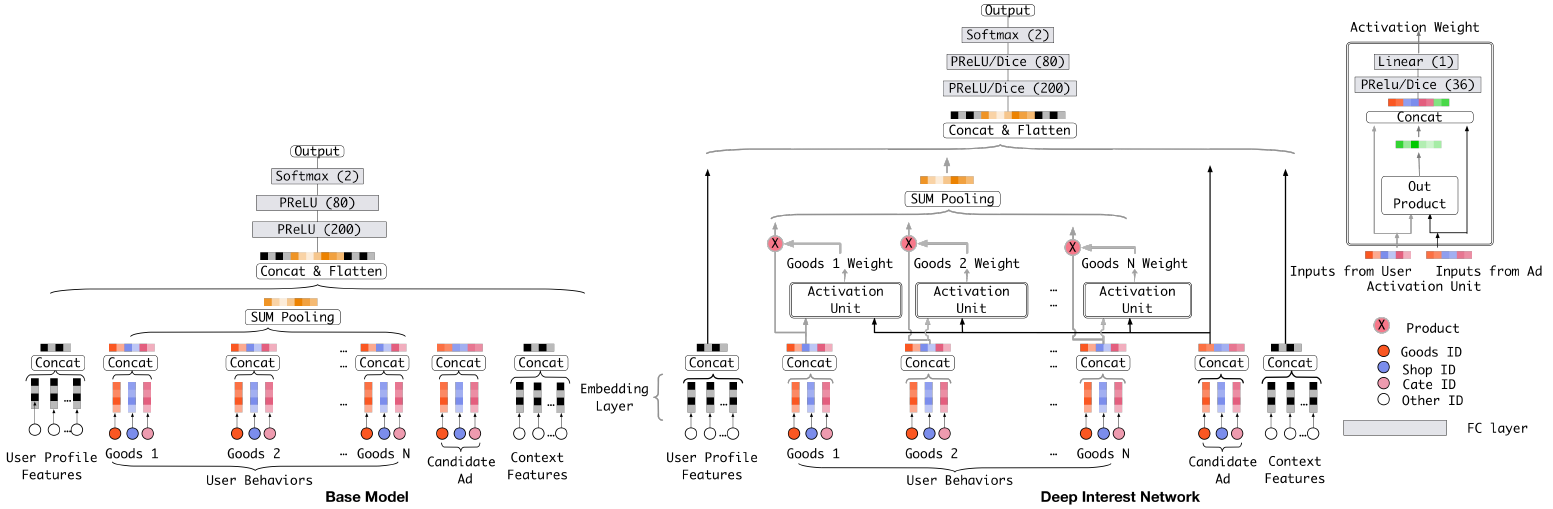
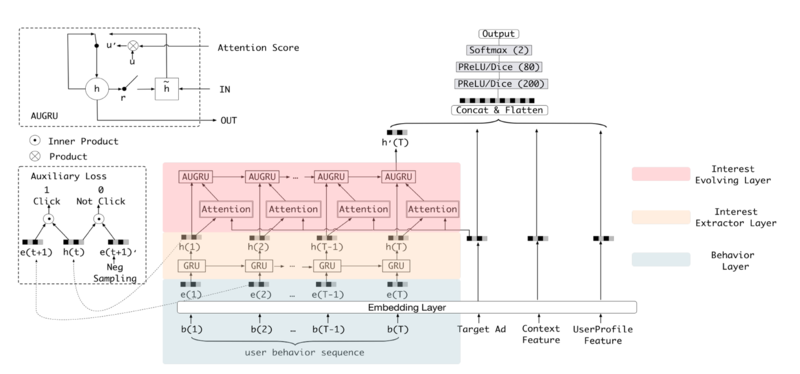
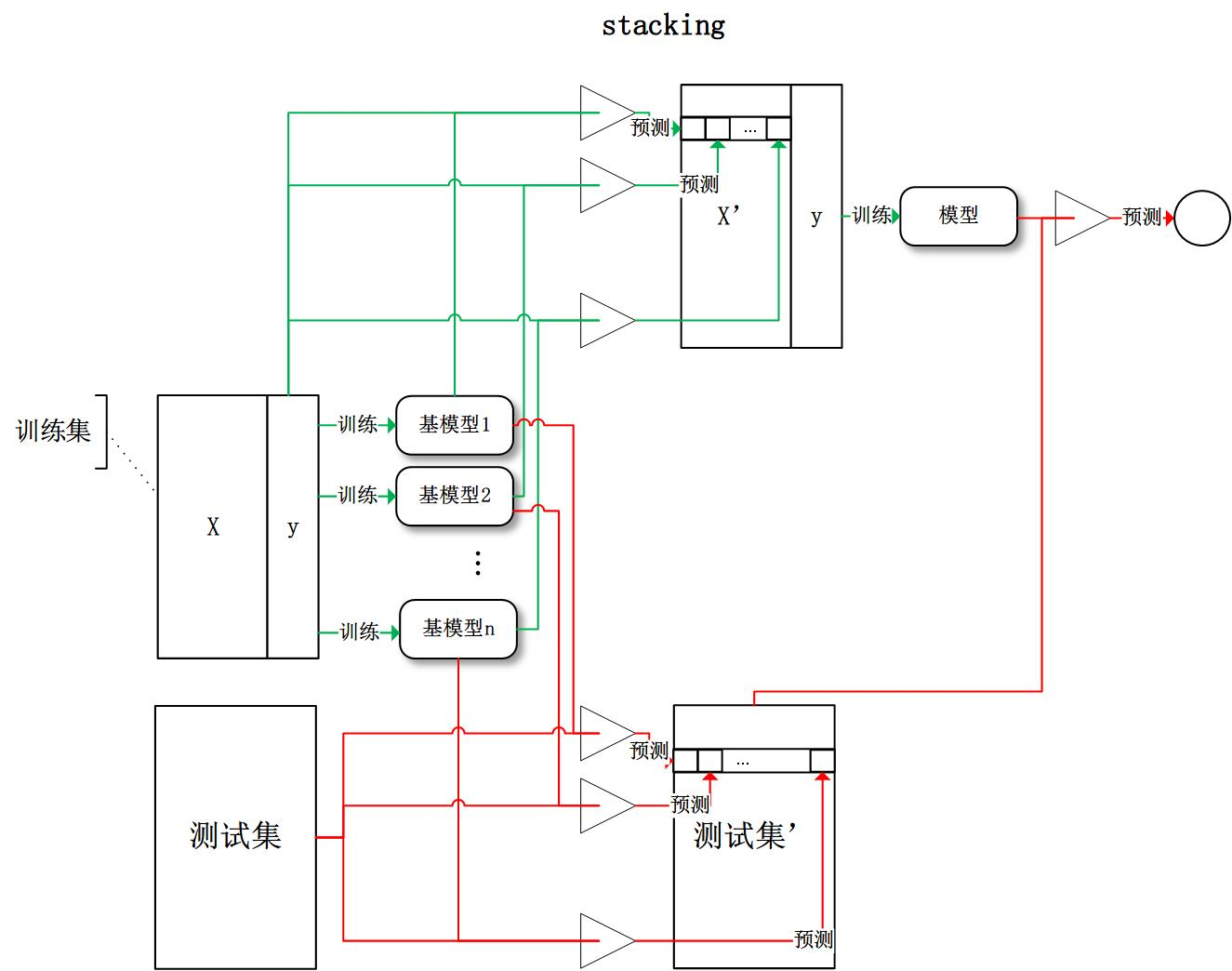
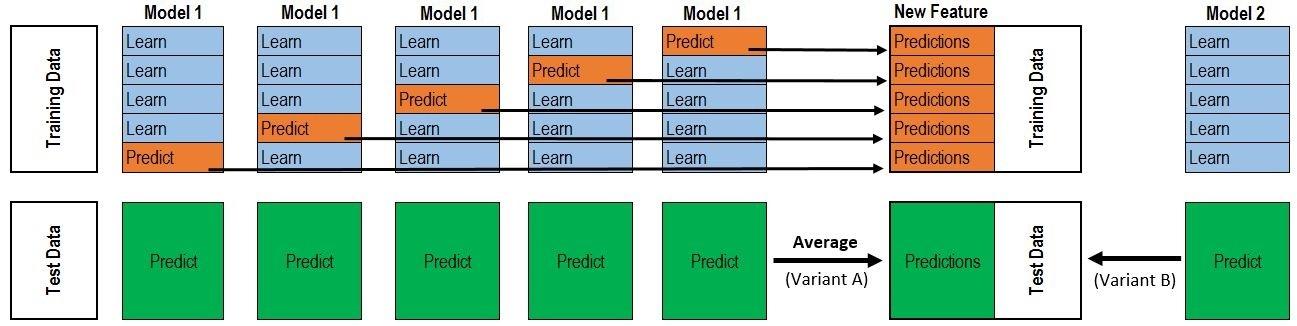
Batch Normalization
Internal Covariate Shift
ICS:由于网络参数变化,引起内部节点(输入)数据分布发生变化的过程
网络中层与层之间高度耦合,具有强关联性
- 网络中任意层都可以视为单独网络
- 上层输入可视为作为当前层外部输入
随训练进行,网络中参数不断发生改变
- 任意层中参数变化会导致之后层输入发生改变
- 高层需要不断适应输入分布的改变,即其输入分布性质影响 该层训练
- 由此导致模型训练困难
负面影响
上层网络需要不断调整输入适应数据分布变换,降低网络学习 效率
输入数据量级不稳定、各维度数据量级差距不稳定
- 降低学习效率
- 小量级维度参数要求更小的学习率
- 否则参数可能在最优解附近反复波动
- 容易出现梯度消失,难以训练饱和非线性模型
- 大量级维度训练过程中容易陷入梯度饱和区,参数更新 速度慢,减缓网络收敛速度
- 训练过程中参数更新更有可能使得输入移向激活函数 饱和区
- 且该效应随着网络深度加深被进一步放大
- 参数初始化需要更复杂考虑
- 降低学习效率
- 还可以使用非饱和激活函数ReLU等避免陷入梯度饱和区
Batch Normalization
Batch Normalization:规范化batch数据,使样本各维度 标准化,即均值为0、方差为1
- $B$:mini-batch
- $z, y$:某层输入向量、规范化后输入向量 (即以个神经元中激活前标量值$z=Wx+b$为一维)
- $\odot$:逐元素乘积
- $E(x)$:均值使用移动平均均值
- $Var(x)$:方差使用移动平均无偏估计
- $\gamma, \beta$:待学习向量,用于恢复网络的表示能力
- $\epsilon$:为数值计算稳定性添加
BN可以视为whitening的简化
- 简化计算过程:避免过高的运算代价、时间
- 保留数据信息:未改变网络每层各特征之间相关性
BN层引入可学习参数$\gamma, \beta$以恢复数据表达能力
- Normalization操作缓解了ICS问题,使得每层输入稳定 ,也导致数据表达能力的缺失
- 输入分布均值为0、方差为1时,经过sigmoid、tanh激活 函数时,容易陷入其线性区域
- $\gamma = \sqrt {Var(z)}, \beta = E(z)$时为等价变换 ,并保留原始输入特征分布信息
- Whitening:白化,对输入数据变换使得各特征同均值、 同方向、不相关,可以分为PCA白化、ZCA白化
训练
规范化在每个神经元内部非线性激活前$z=Wu$进行,而不是 [也]在上一层输出$u$上进行,即包含BN最终为
- $act$:激活函数
- 偏置$b$:可以被省略,BN中减去均值
- $u$的分布形状可以在训练过程中改变
- 而$u$两次正则化无必要
- $z=Wu$分布更可能对称、稠密、类似高斯分布
以batch统计量作为整体训练样本均值、方差估计
- 每层均需存储均值、方差的移动平均统计量用于测试时 归一化测试数据
对卷积操作,考虑卷积特性,不是只为激活函数(即卷积核) 学习$\gamma, \beta$,而是为每个feature map学习 (即每个卷积核、对每个特征图层分别学习)
预测
预测过程中各参数(包括均值、方差)为定值,BN仅仅对数据 做了线性变换
使用训练总体的无偏统计量对测试数据归一化 (训练时存储)
还可以使用样本指数加权平均统计量
用途
- BN通过规范化输入数据各维度分布减少ICS,使得网络中每层 输入数据分布相对稳定
实现网络层与层之间的解耦
- 方便迁移学习
- 加速模型学习速度:后层网络无需不断适应输入分布变化, 利于提高神经网络学习速度
降低模型对网络超参数、初始值敏感度,使得网络学习更加稳定
- 简化调参过程
- 允许使用更大的学习率提高学习效率
- $a$:假设某层权重参数变动$a$倍
- 激活函数函数输入不受权重$W$放缩影响
- 梯度反向传播更稳定,权重$W$的Jacobian矩阵将包含接近 1的奇异值,保持梯度稳定反向传播
允许网络使用饱和激活函数(sigmoid、tanh等),而不至于 停滞在饱和处,缓解梯度消失问题
- 深度网络的复杂性容易使得网络变化积累到上层网络中, 导致模型容易进入激活函数梯度饱和区
有正则化作用,提高模型泛化性能,减少对Dropout的需求
- 不同batch均值、方差有所不同,为网络学习过程增加随机 噪声
- 与Dropout关闭神经元给网络带来噪声类似,一定程度上 有正则化效果
Layer Normalization
层归一化:假设非线性激活前的输入随机变量分布接近,可以直接 基于每层所有非线性激活前输入估计均值、方差
- $h^l$:第$l$隐层激活前值
- $\mu^l, \sigma^l$:第$l$隐层对应LN均值、方差 (标量,是同层神经元激活前值统计量)
相对于BN,其适应范围更广
- 循环神经网络中,BN无法处理长于训练序列的测试序列
- BN无法应用到在线学习、超大分布式模型任务,此时训练 batch较小,计算的均值、方差无法有效代表训练总体
LN假设非线性激活前输入随机变量分布接近,而CNN网络中图像 边缘对应kernel大量隐藏单元未被激活,假设不成立,所以 CNN网络中LN效果没有BN效果好