模型

• 模型是策略的工具，策略包含模型，是模型的延伸

  • 相较于专家规则，机器学习模型
    • 允许加入更多特征维度，描述更加全面
    • 上限更高、下限更低
    • 涉及更多维度特征时，维护更方便
  • 机器学习模型和专家规则并非相互替代，更多的是串联

• 业务问题转换为带解决数学问题

  • 尽量将业务问题转换为更容易解决分类问题而不是回归问题
  • 数学问题应尽量贴近业务：评估指标好不等于业务价值高
    • 远离业务问题的训练出模型，其线下评估效果好也不意味着上线效果好，如：针对客户而不是订单评价
    • 影响客户体验，如：客户等待时间预估偏低而不是偏高

• 样本构造

  • 标签定义
    • 尽量为客观事实（是否、数量），而非主观判断（等级）
    • 样本粒度贴合实际、业务（订单粒度、客户粒度）
  • 样本数量
    • 二分类场景：正例样本大于 2000，占比超过 1%
  • 采样
    • 尽量不进行人工采样，保持训练数据正、负例比例和真实情况对齐

传统评分卡

• 信用评分卡模型：利用模型将账户的属性特征按取值分组、并赋予一定分数，对账户进行信用评分

  • 最常见的金融风控手段之一，用于决定是否给予授信以及授信的额度和利率
  • 常用逻辑回归作为模型
  • 应用形式为查分组得分表、得分加和
    • 变量总是被分组，同组内得分相同
    • 用户属性变化不足以跨越箱边界，则得分不改变

• 评分卡更关注得分相对值，即得分变动情况，评分绝对值含义意义不大

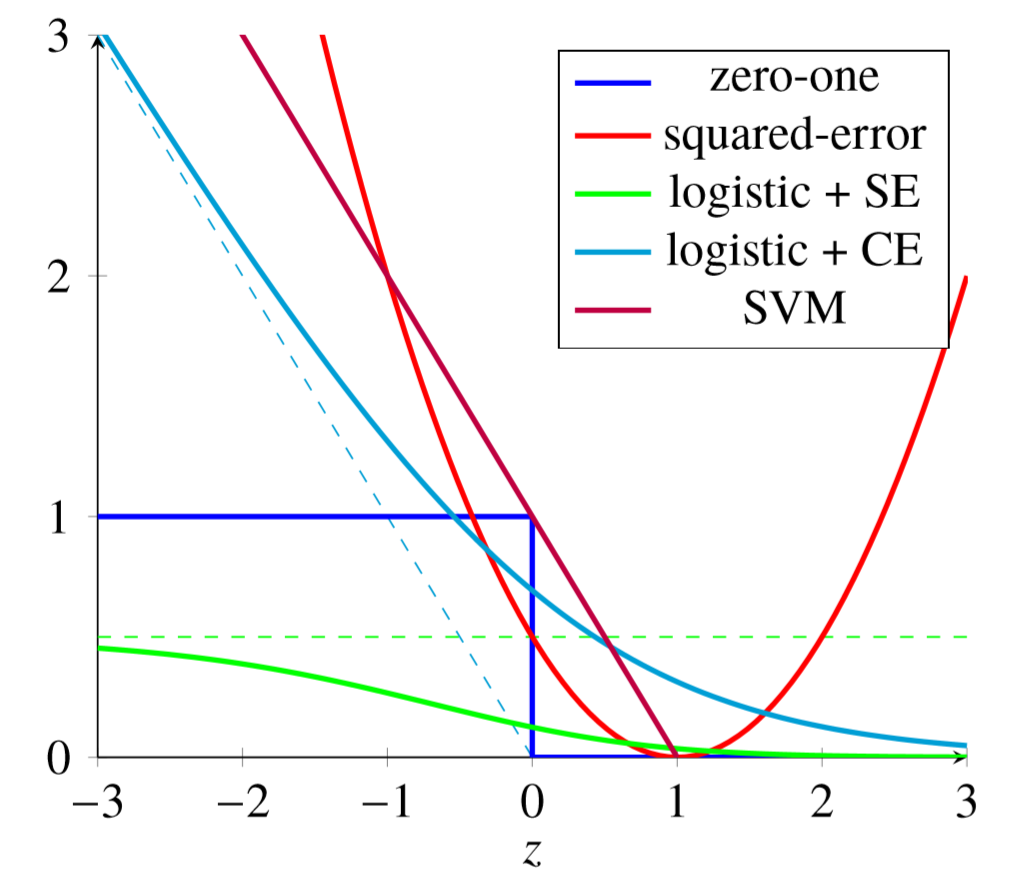
  • 常用 LR 中 sigmoid 函数内线性函数结果作为初始得分
    • 根据 LR 意义，此时得分可以映射为账户的违约概率
  • 为美观，可能会对得分做线性变换
    • 常对各特征得分做放缩、对账户得分和做平移，此时放缩比例除以 $ln2$ 即为 PDO （对特征得分同时做等比例放缩、平移可行但蠢）
    • 线性变换后得分绝对值无意义，特征重要性可用特征各分组得分差距衡量

• 评分卡在不同业务阶段体现的方式、功能不一样，按照借贷用户借贷时间可以分为

  • 申请评分卡 Application Score Card：贷前申请评分卡
  • 行为评分卡 Behavior Score Card：贷中行为评分卡
  • 催收评分卡 Collection Score Card：贷后催收评分卡

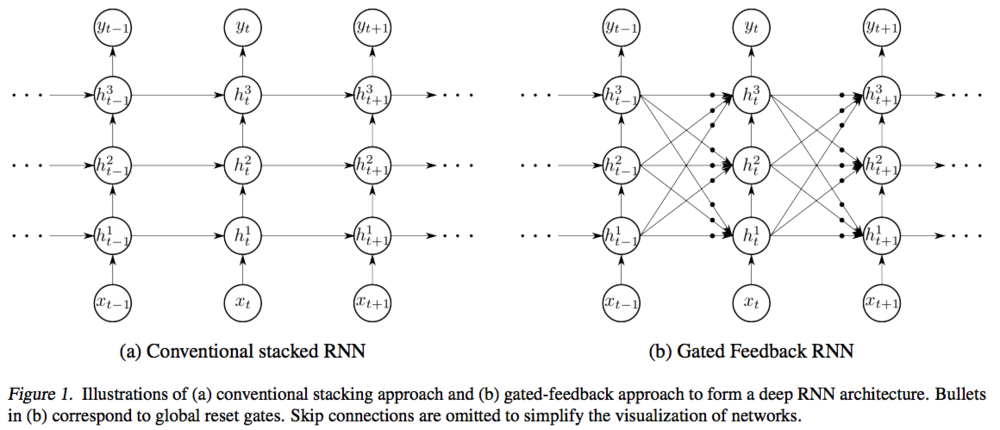
Stacking 评分卡

• 考虑将评分卡、机器学习模型结合，使用机器学习模型构建特征，在此基础之上建立评分卡模型

• Stacking 思想下的模型架构

  • 原始数据域
  • 数据挖掘、特征工程
  • 数据域特征子模型
  • 评分卡模型

• 架构优势

  • 可解释性：保留在数据域粒度上的可解释性
  • 信息提取：子模型提取弱特征信息，降低特征工程门槛
  • 维度多样性：特征子模型机制，降低特征筛选必要性，保证各数据域都有特征入模
  • 模块化：具有良好扩展性，支持子模型替换、删除
  • 并行化：各数据域特征子模型专业、独立负责，提高效率

• 架构劣势

  • 牺牲部分可解释性：若策略、模型使用相同变量，策略阈值调整对模型影响难以估计
    • 控制入模变量数目，便于快速定位
    • 利用 SHAP、LIME 等工具解释模型
  • 增加上线、维护成本：需要上线多个模型，且对多个架构多个层次都进行监控
  • 协同建模增加对接成本
  • 分数据域特征子模型建模，容易造成数据孤岛，无法捕捉不同数据域间的数据联系
    • 跨数据域构造特征，构建跨数据域子模型

B 卡 - Behavior Scoring

贷中风控：根据借款人放贷后行为表现，预测未来逾期风险

• B 卡用于动态监控放款后风险变化

  • 贷前阶段对借款人履约行为掌握少，且为静态数据
  • 一般无需实时，离线T+1计算即可

• B 卡适合的信贷场景

  • 还款周期长
    • 长周期场景用户风险变化可能性大，与 A 卡形成区分
    • 引入贷中客户信息、还款履约行为，更准确识别客户逾期风险
  • 循环授信
    • 贷前阶段，无法很好识别客户风险，设置初始额度
    • 贷中与客户更多交互之后，可根据获取的贷中行为信息进行提额、降额操作

• B 卡区分度一般很高

  • 除贷前数据之外，还可以使用账户的贷中表现数据
  • 特别的，不考虑排序性的情况下，使用是否逾期作为划分依据也能得到较高的 TPR-FPR，给出 KS 的下限

• B 卡建模主要基于老客

  • 老客有足够长的申贷、还款记录
  • 新、老客定义口径
    • 新客：无历史结清订单
    • 老客：至少有1笔结清订单

C 卡 - Collection Scoring

贷后催收评分卡：当前状态为逾期情况下，预测未来出催可能性

• 现阶段业界对 C 卡不够重视

  • 贷前风控最重要，优秀的贷前带来更容易的贷中、贷后
  • 催收效果和人员更相关，而逾期发生之后往往会委外
  • 随信贷行业的发展，贷后催收会趋向于精细化、专业化的发展，模型+策略的优化愈发重要

• 模型分群

  • 新老入催用户
    • 首次入催
    • 再次入催
  • MOB 信息（数据厚薄）
    • 还款月份数
    • 催记月份数
  • 订单详情
    • 利率
    • 期限
    • 金额

样本选择

• 建模样本窗口选择

  • 特征覆盖度：保证数据厚薄程度相同
  • 催收动作变化：出催没有大幅度变动
  • 客群变化：入催没有大幅变动

• 同用户订单合案

  • 不合案：同用户多笔订单视为不同样本
    • 表现期内入催当期结清视为出催
  • 合案：同用户相近观察点入催订单合并
    • 表现期内入催当期所有账单还清视为出催
    • 对发生过 M2+ 逾期者，可将只要出催一期即视为出催

C 卡模型

• 根据模型作用时间段分类

• M1 全量模型：预测 M1 阶段（逾期 30 天内）还款概率

  • 样本：所有入催样本整体
    • 若缓催期内催出用户较多，则模型主要学习了缓催样本信息，约等于缓催响应模型，对非缓催样本效果较差
  • 时间窗口
    • 观察点：还款日
    • 表现期：M1 阶段

• 缓催响应模型：预测适合缓催人群

  • 样本：需要积累足够的缓催响应样本
    • 若有足够缓催响应样本，可以和M1全量模型同时构建
    • 否则，在 M1 全量模型得分高（出催概率高）人群上进行 AB Test，积累缓催响应样本
  • 时间窗口
    • 观察点：还款日
    • 表现期：缓催响应日(2-3 天)

• 贷后 N 天流转模型：预测贷后N天后的还款概率

  • 样本：缓催内未出催样本
    • 去除缓催样本影响，更多学习缓催期外出催样本信息
    • 优先对催出概率高的人群进行催收，提高出催概率
  • 时间窗口
    • 观察点：还款日（逾期）后 N 天
    • 表现期：至下个流转模型观察点、逾期阶段结束时间点

• M2+ 模型：预测 M2+ 阶段的还款概率（类似贷后流转模型）

  • 样本：M1 阶段未出催样本
  • 时间窗口
    • 观察点：M2 阶段起始
    • 表现期：至下个流转模型观察点、逾期阶段结束时间点

模型应用方法

• 缓催响应人群确定

  • 交叉 M1 模型、缓催响应模型，根据模型交叉结果设置阈值
  • 根据阈值筛选缓催响应人群
  • 限定缓催期（2-3 天），将缓催响应样本分为人工催收、缓催两组，观察两组在缓催期限内出催率变化
    • 若出催率相同，则认为缓催响应人群分析方法可行，对缓催响应人群可采取缓催策略
    • 若出催率相差较大，则调整缓催响应人群分析方法

  • 缓催模型响应时间（缓催期）可根据响应时间段内的出催率变化设置

• 模型搭建策略

  • M1 阶段出催概率较大，在M1阶段会设计多个细分模型
    • 至少：M1 阶段全量模型
    • 缓催样本足够
      • 缓催响应模型
      • 贷后 N 天流转模型
    • 精细化管理：多个不同时间窗口的贷后流转模型
  • M2+ 阶段根据样本量、精细化程度设置适量模型

开发流程标准化

• 风控模型开发流程标准化意义
  • 提高建模效率：可批量快速生产模型，提高效率
  • 帮助理解指标逻辑、业务含义，利于调试优化
  • 流程规范约束
    • 统一建模流程，减少出错概率、便于问题回溯
    • 统一命名方式，便于汇总文档

数据预处理

特征编码

• 特征离散化

• WOE 编码特征

  • WOE 曲线应符合业务逻辑（一般单调），并且经过跨时间 窗口验证，否则应该调整
  • LR 模型中特征权重应该全为正值，否则
    • 同数据 WOE 值体现的逻辑相违背
    • 负值权重特征存在较严重共线性

• one-hot 编码特征

  • 同特征下个分箱单独作为独立变量取值
    • 权重灵活性更大，模型效果可能较好
    • 变量数量多，需要样本数量大，模型效果可能较差（随机解法）
  • 各特征分箱之间无联系，难以通过模型剔除某个变量

样本赋权

• 样本赋权：充分利用所有样本的信息，避免样本有偏
  • 按样本距今时间赋权，近期样本高权重
  • 按业务特性赋权，不同额度、利率、期限不同权重
  • 按账户类型赋权

拒绝推断

• Reject Inference 拒绝推断：避免样本偏差导致模型估计过于乐观

Exploratory Data Analysis

• 风控领域样本较少，一般按月粒度观察，即将样本按月分组为 vintage 进行分析，探索、评估数据

  • 稳定性
  • 信息量
  • 信息重复/相关性

• 实操中可逐阶段设置多组阈值，分布进行变量探索、筛选

  • 多组阈值逐步剔除能尽可能保留高信息量特征
  • 避免相关性、RF 特征重要度等 非单变量指标 剔除过多特征

模型评估

• 有效性/区分度

  • GINI 指数
  • KS 值
  • 坏样本率：组内、累计
  • 提升度 = 召回样本坏样本率 / 全部样本坏样本率
  • odds = 坏样本率 / 好样本率

• 排序性

  • AUC 值/ROC 曲线

• 稳定性

  • PSI
  • 各 Vintage 内坏占比、Lift 值、odds 等指标稳定性

• 模型得分展示表

  • 箱内样本数
  • 好、坏样本数
  • 箱内坏样本、比例
  • 累计好、坏样本
  • 累计好、坏样本比例：TPR、FPR、TPR-FPR
  • 累计通过率、坏样本比例

模型应用

Calibration 模型校准

• 一致性校准：将模型预测概率校准到真实概率
• 尺度变换：将风险概率转换为整数分数

导出得分

• 原始得分

  • one-hot 编码：LR 模型系数
  • WOE 编码：LR 模型系数（权重）、WOE 值之积

• 常对各特征得分做放缩、对账户得分和做平移

  • PDO：违约翻倍得分
    • 用于缩放原始得分
    • 得分按 $\frac {PDO} {ln2}$ 缩放后，得分减少 $PDO$ 分，用户违约 odds 翻倍，缺省即 $ln2$
  • 账户得分总和平移则仅仅是为了美观

  • 对特征得分同时做等比例放缩、平移可行但蠢

LightGBM

逻辑斯蒂回归

逻辑斯蒂分布

• $\mu$：位置参数
• $\gamma$：形状参数

• 分布函数属于逻辑斯蒂函数

• 分布函数图像为sigmoid curve

  • 关于的$(\mu, \frac 1 2)$中心对称 $$F(-x+\mu) - \frac 1 2 = -F(x+\mu) + \frac 1 2$$
  • 曲线在靠近$\mu$中心附近增长速度快，两端速度增长慢
  • 形状参数$\gamma$越小，曲线在中心附近增加越快

• 模型优点

  • 模型输出值位于0、1之间，天然具有概率意义，方便观测 样本概率分数
  • 可以结合$l-norm$正则化解决过拟合、共线性问题
  • 实现简单，广泛用于工业问题
  • 分类时计算量比较小、速度快、消耗资源少

• 模型缺点

  • 特征空间很大时，性能不是很好，容易欠拟合，准确率一般
  • 对非线性特征需要进行转换

Binomial Logistic Regression Model

二项逻辑斯蒂回归模型：形式为参数化逻辑斯蒂分布的二分类 生成模型

• $w, b$：权值向量、偏置
• $\hat x = (x^T|1)^T$
• $\hat w = (w^T|b)^T$

• 逻辑回归比较两个条件概率值，将实例$x$归于条件概率较大类

• 通过逻辑回归模型，可以将线性函数$wx$转换为概率

  • 线性函数值越接近正无穷，概率值越接近1
  • 线性函数值越接近负无穷，概率值越接近0

Odds/Odds Ratio

• 在逻辑回归模型中，输出$Y=1$的对数几率是输入x的线性函数

  $$log \frac {P(Y=1|x)} {1-P(Y=1|x)} = \hat w \hat x$$

• OR在逻辑回归中意义：$x_i$每增加一个单位，odds将变为原来 的$e^{w_i}$倍

  $$\begin{align*} odd &= \frac {P(Y=1|x)} {1-P(Y=1|x)} = e^{\hat w \hat x} \\ OR_{x_i+1 / x_i} &= e^{w_i} \end{align*}$$

  • 对数值型变量

    • 多元LR中，变量对应的系数可以计算相应 Conditional OR
    • 可以建立单变量LR，得到变量系数及相应 Marginal OR

  • 对分类型变量

    • 可以直接计算变量各取值间对应的OR
    • 变量数值化编码建立模型，得到变量对应OR

    • 根据变量编码方式不同，变量对应OR的含义不同，其中 符合数值变量变动模式的是WOE线性编码

策略

极大似然：极小对数损失（交叉熵损失）

• $\pi(x) = P(Y=1|x)$

算法

• 通常采用梯度下降、拟牛顿法求解有以上最优化问题

Multi-Nominal Logistic Regression Model

多项逻辑斯蒂回归：二项逻辑回归模型推广

• 策略、算法类似二项逻辑回归模型

Generalized Linear Model

todo

Maximum Entropy Model

最大熵原理

最大熵原理：学习概率模型时，在所有可能的概率模型（分布）中， 熵最大的模型是最好的模型

• 使用约束条件确定概率模型的集合，则最大熵原理也可以表述为 在满足约束条件的模型中选取熵最大的模型

• 直观的，最大熵原理认为

  • 概率模型要满足已有事实（约束条件）
  • 没有更多信息的情况下，不确定部分是等可能的
  • 等可能不容易操作，所有考虑使用可优化的熵最大化 表示等可能性

最大熵模型

最大熵模型为生成模型

• 对给定数据集$T={(x_1,y_1),\cdots,(x_N,y_N)}$，联合分布 P(X,Y)、边缘分布P(X)的经验分布如下

  $$\begin{align*} \tilde P(X=x, Y=y) & = \frac {v(X=x, Y=y)} N \\ \tilde P(X=x) & = \frac {v(X=x)} N \end{align*}$$

  • $v(X=x,Y=y)$：训练集中样本$(x,y)$出频数

• 用如下feature function $f(x, y)$描述输入x、输出y之间 某个事实

  $$f(x, y) = \left \{ \begin{array}{l} 1, & x、y满足某一事实 \\ 0, & 否则 \end{array} \right.$$

  • 特征函数关于经验分布$\tilde P(X, Y)$的期望

    $$E_{\tilde P} = \sum_{x,y} \tilde P(x,y)f(x,y)$$

  • 特征函数关于生成模型$P(Y|X)$、经验分布$\tilde P(X)$ 期望

    $$E_P(f(x)) = \sum_{x,y} \tilde P(x)P(y|x)f(x,y)$$

• 期望模型$P(Y|X)$能够获取数据中信息，则两个期望值应该相等

  $$\begin{align*} E_P(f) & = E_{\tilde P}(f) \\ \sum_{x,y} \tilde P(x)P(y|x)f(x,y) & = \sum_{x,y} \tilde P(x,y)f(x,y) \end{align*}$$

  此即作为模型学习的约束条件

  • 此约束是纯粹的关于$P(Y|X)$的约束，只是约束形式特殊， 需要通过期望关联熵

  • 若有其他表述形式、可以直接带入的、关于$P(Y|X)$约束， 可以直接使用

• 满足所有约束条件的模型集合为 $$\mathcal{C} = \{P | E_{P(f_i)} = E_{\tilde P (f_i)}, i=1,2,\cdots,n \}$$ 定义在条件概率分布$P(Y|X)$上的条件熵为 $$H(P) = -\sum_{x,y} \tilde P(x) P(y|x) logP(y|x)$$ 则模型集合$\mathcal{C}$中条件熵最大者即为最大是模型

策略

最大熵模型的策略为以下约束最优化问题

• 引入拉格朗日函数

  $$\begin{align*} L(P, w) & = -H(P) - w_0(1-\sum_y P(y|x)) + \sum_{m=1}^M w_m(E_{\tilde P}(f_i) - E_P(f_i)) \\ & = \sum_{x,y} \tilde P(x) P(y|x) logP(y|x) + w_0 (1-\sum_y P(y|x)) + \sum_{m=1}^M w_m (\sum_{x,y} \tilde P(x,y)f_i(x, y) - \tilde P(x)P(y|x)f_i(x,y)) \end{align*}$$

  • 原始问题为

    $$\min_{P \in \mathcal{C}} \max_{w} L(P, w)$$

  • 对偶问题为

    $$\max_{w} \min_{P \in \mathcal{C}} L(P, w)$$

  • 考虑拉格朗日函数$L(P, w)$是P的凸函数，则原始问题、 对偶问题解相同

• 记

  $$\begin{align*} \Psi(w) & = \min_{P \in \mathcal{C}} L(P, w) = L(P_w, w) \\ P_w & = \arg\min_{P \in \mathcal{C}} L(P, w) = P_w(Y|X) \end{align*}$$

• 求$L(P, w)$对$P(Y|X)$偏导

  $$\begin{align*} \frac {\partial L(P, w)} {\partial P(Y|X)} & = \sum_{x,y} \tilde P(x)(logP(y|x)+1) - \sum_y w_0 - \sum_{x,y}(\tilde P(x) \sum_{i=1}^N w_i f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x)(log P(y|x) + 1 - w_0 - \sum_{i=1}^N w_i f_i(x, y)) \end{align*}$$

  偏导置0，考虑到$\tilde P(x) > 0$，其系数必始终为0，有

  $$\begin{align*} P(Y|X) & = \exp(\sum_{i=1}^N w_i f_i(x,y) + w_0 - 1) \\ & = \frac {exp(\sum_{i=1}^N w_i f_i(x,y))} {exp(1-w_0)} \end{align*}$$

• 考虑到约束$\sum_y P(y|x) = 1$，有

  $$\begin{align*} P_w(y|x) & = \frac 1 {Z_w(x)} exp(\sum_{i=1}^N w_i f_i(x,y)) \\ Z_w(x) & = \sum_y exp(\sum_{i=1}^N w_i f_i(x,y)) \\ & = exp(1 - w_0) \end{align*}$$

  • $Z_w(x)$：规范化因子
  • $f(x, y)$：特征
  • $w_i$：特征权值

• 原最优化问题等价于求解偶问题极大化问题$\max_w \Psi(w)$

  $$\begin{align*} \Psi(w) & = \sum_{x,y} \tilde P(x) P_w(y|x) logP_w(y|x) + \sum_{i=1}^N w_i(\sum_{x,y} \tilde P(x,y) f_i(x,y) - \sum_{x,y} \tilde P(x) P_w(y|x) f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) + \sum_{x,y} \tilde P(x,y) P_w(y|x)(log P_w(y|x) - \sum_{i=1}^N w_i f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_{x,y} \tilde P(x,y) P_w(y|x) log Z_w(x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_x \tilde P(x) log Z_w(x) \end{align*}$$

  记其解为

  $$w^{*} = \arg\max_w \Psi(w)$$

  带入即可得到最优（最大熵）模型$P_{w^{*}}(Y|X)$

策略性质

• 已知训练数据的经验概率分布为$\tilde P(X,Y)$，则条件概率 分布$P(Y|X)$的对数似然函数为

  $$\begin{align*} L_{\tilde P}(P_w) & = N log \prod_{x,y} P(y|x)^{\tilde P(x,y)} \\ & = \sum_{x,y} N * \tilde P(x,y) log P(y|x) \end{align*}$$

  • 这里省略了系数样本数量$N$

• 将最大熵模型带入，可得

  $$\begin{align*} L_{\tilde P_w} & = \sum_{x,y} \tilde P(y|x) logP(y|x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_{x,y} \tilde P(x,y)log Z_w(x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_x \tilde P(x) log Z_w(x) \\ & = \Psi(w) \end{align*}$$

  对偶函数$\Psi(w)$等价于对数似然函数$L_{\tilde P}(P_w)$， 即最大熵模型中，对偶函数极大等价于模型极大似然估计

改进的迭代尺度法

• 思想

  • 假设最大熵模型当前参数向量$w=(w_1,w_2,\cdots,w_M)^T$
  • 希望能找到新的参数向量（参数向量更新） $w+\sigma=(w_1+\sigma_1,\cdots,w_M+\sigma_M)$ 使得模型对数似然函数/对偶函数值增加
  • 不断对似然函数值进行更新，直到找到对数似然函数极大值

• 对给定经验分布$\tilde P(x,y)$，参数向量更新至$w+\sigma$ 时，对数似然函数值变化为

  $$\begin{align*} L(w+\sigma) - L(w) & = \sum_{x,y} \tilde P(x,y) log P_{w+\sigma}(y|x) - \sum_{x,y} \tilde P(x,y) log P_w(y|x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) - \sum_x \tilde P(x) log \frac {Z_{w+\sigma}(x)} {Z_w(x)} \\ & \geq \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \frac {Z_{w+\sigma}(x)} {Z_w(x)} \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_y(y|x) exp(\sum_{i=1}^M \sigma_i f_i(x,y)) \end{align*}$$

  • 不等式步利用$a - 1 \geq log a, a \geq 1$

  • 最后一步利用

    $$\begin{align*} \frac {Z_{w+\sigma}(x)} {Z_w(x)} & = \frac 1 {Z_w(x)} \sum_y exp(\sum_{i=1}^M (w_i + \sigma_i) f_i(x, y)) \\ & = \frac 1 {Z_w(x)} \sum_y exp(\sum_{i=1}^M w_i f_i(x,y) + \sigma_i f_i(x,y)) \\ & = \sum_y P_w(y|x) exp(\sum_{i=1}^n \sigma_i f_i(x,y)) \end{align*}$$

• 记上式右端为$A(\sigma|w)$，则其为对数似然函数改变量的 一个下界

  $$L(w+\sigma) - L(w) \geq A(\sigma|w)$$
  • 若适当的$\sigma$能增加其值，则对数似然函数值也应该 增加
  • 函数$A(\sigma|w)$中因变量$\sigma$为向量，难以同时 优化，尝试每次只优化一个变量$\sigma_i$，固定其他变量 $\sigma_j$

• 记

  $$f^{**} (x,y) = \sum_i f_i(x,y)$$

  考虑到$f_i(x,y)$为二值函数，则$f^{**}(x,y)$表示所有特征 在$(x,y)$出现的次数，且有

  $$A(\sigma|w) = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_w(y|x) exp(f^{**}(x,y) \sum_{i=1}^M \frac {\sigma_i f_i(x,y)} {f^{**}(x,y)})$$

• 考虑到$\sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} = 1$， 由指数函数凸性、Jensen不等式有

  $$exp(\sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} \sigma_i f^{**}(x,y)) \leq \sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} exp(\sigma_i f^{**}(x,y))$$

  则

  $$A(\sigma|w) \geq \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_w(y|x) \sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} exp(\sigma_i f^{**}(x,y))$$

• 记上述不等式右端为$B(\sigma|w)$，则有

  $$L(w+\sigma) - L(w) \geq B(\sigma|w)$$

  其为对数似然函数改变量的一个新、相对不紧的下界

• 求$B(\sigma|w)$对$\sigma_i$的偏导

  $$\frac {\partial B(\sigma|w)} {\partial \sigma_i} = \sum_{x,y} \tilde P(x,y) f_i(x,y) - \sum_x \tilde P(x) \sum_y P_w(y|x) f_i(x,y) exp(\sigma_i f^{**}(x,y))$$

  置偏导为0，可得

  $$\sum_x \tilde P(x) \sum_y P_w(y|x) f_i(x,y) exp(\sigma_i f^{**}(x,y)) = \sum_{x,y} \tilde P(x,y) f_i(x,y) = E_{\tilde P}(f_i)$$

  其中仅含变量$\sigma_i$，则依次求解以上方程即可得到 $\sigma$

算法

• 输入：特征函数$f_1, f_2, \cdots, f_M$、经验分布 $\tilde P(x)$、最大熵模型$P_w(x)$
• 输出：最优参数值$wi^{*}$、最优模型$P{w^{*}}$

1. 对所有$i \in {1,2,\cdots,M}$，取初值$w_i = 0$

2. 对每个$i \in {1,2,\cdots,M}$，求解以上方程得$\sigma_i$

   • 若$f^{**}(x,y)=C$为常数，则$\sigma_i$有解析解

     $$\sigma_i = \frac 1 C log \frac {E_{\tilde P}(f_i)} {E_P(f_i)}$$

   • 若$f^{**}(x,y)$不是常数，则可以通过牛顿法迭代求解

     $$\sigma_i^{(k+1)} = \sigma_i^{(k)} - \frac {g(\sigma_i^{(k)})} {g^{'}(\sigma_i^{(k)})}$$

     • $g(\sigma_i)$：上述方程对应函数

     • 上述方程有单根，选择适当初值则牛顿法恒收敛

3. 更新$w_i$，$w_i \leftarrow w_i + \sigma_i$，若不是所有 $w_i$均收敛，重复2

BFGS算法

对最大熵模型

• 为方便，目标函数改为求极小

  $$\begin{array}{l} \min_{w \in R^M} f(w) = \sum_x \tilde P(x) log \sum_{y} exp(\sum_{i=1}^M w_i f_i(x,y)) - \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M w_i f_i(x,y) \end{array}$$

• 梯度为

  $$\begin{align*} g(w) & = (\frac {\partial f(w)} {\partial w_i}, \cdots, \frac {\partial f(w)} {\partial w_M})^T \\ \frac {\partial f(w)} {\partial w_M} & = \sum_{x,y} \tilde P(x) P_w(y|x) f_i(x,y) - E_{\tilde P}(f_i) \end{align*}$$

算法

将目标函数带入BFGS算法即可

• 输入：特征函数$f_1, f_2, \cdots, f_M$、经验分布 $\tilde P(x)$、最大熵模型$P_w(x)$
• 输出：最优参数值$wi^{*}$、最优模型$P{w^{*}}$

1. 取初值$w^{(0)}$、正定对称矩阵$B^{(0)}$，置k=0

2. 计算$g^{(k)} = g(w^{(k)})$，若$|g^{(k)}| < \epsilon$， 停止计算，得到解$w^{*} = w^{(k)}$

3. 由拟牛顿公式$B^{(k)}p^{(k)} = -g^{(k)}$求解$p^{(k)}$

4. 一维搜索，求解

   $$\lambda^{(k)} = \arg\min_{\lambda} f(w^{(k)} + \lambda p_k)$$

5. 置$w^{(k+1)} = w^{(k)} + \lambda^{(k)} p_k$

6. 计算$g^{(k+1)} = g(w^{(k+1)})$，若 $|g^{(k+1)}| < \epsilon$，停止计算，得到解 $w^{*} = w^{(k+1)}$，否则求

   $$B^{(k+1)} = B^{(k)} - \frac {B^{(k)} s^{(k)} (s^{(k)})^T B^{(k)}} {(s^{(k)})^T B^{(k)} s^{(k)}} + \frac {y^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}}$$

   • $s^{(k)} = w^{(k+1)} - w^{(k)}$
   • $y^{(k)} = g^{(k+1)} - g^{(k)}$

7. 置k=k+1，转3

损失函数

• 损失函数可以视为模型与真实的距离的度量
  • 因此损失函数设计关键即，寻找可以代表模型与真实的距离的统计量
  • 同时为求解方便，应该损失函数最好应满足导数存在

Surrogate Loss

代理损失函数：用优化方便的损失函数代替难以优化的损失函数，间接达到优化原损失函数的目标

• 如 0-1 损失难以优化，考虑使用二次损失、交叉熵损失替代

损失函数设计

• 对有监督学习：真实 已知，可以直接设计损失函数

• 对无监督学习：真实 未知，需要给定 真实标准

  • NLP：需要给出语言模型
  • EM 算法：熵最大原理

常用损失函数

0-1 Loss

• 0-1 损失函数梯度要么为 0、要么不存在，无法通过梯度下降方法优化 0-1 损失

• 适用场合

  • 二分类：Adaboost
  • 多分类：Adaboost.M1

Quadratic / Squared Error Loss

• 平方错误损失函数可导，可以基于梯度下降算法优化损失函数

• 适用场合

  • 回归预测：线性回归
  • 分类预测：0-1 二分类（根据预测得分、阈值划分）

Logistic SE

• 平方损失用于二分类时存在如下问题（模型输出无限制）

  • 若模型对某样本非常确信为正例，给出大于1预测值
  • 此时模型会进行不必要、开销较大的优化

• 考虑对模型输出进行 sigmoid 变换后作为预测值，再应用平方错误损失函数

  $$L(y, f(x)) = \frac 1 2 (y - \sigma(f(x)))^2$$
  • Logistic SE 损失函数曲线对 0-1 损失拟合优于平方损失
  • 但负区间存在饱和问题，损失最大只有 0.5

Cross Entropy

交叉熵损失

• $y$：样本实际值
• $f(x)$：各类别预测概率
• $K$：分类数目

• 交叉熵损失综合二次损失、logistic SE 优势，以正样本为例

  • 预测值较大时：损失接近 0，避免无效优化
  • 预测值较小时：损失偏导趋近于 -1，不会出现饱和现象

• $y$ 为 one-hot 编码时实际值时

  • 分类问题仅某分量为 1：此时交叉熵损失同对数损失（负对数极大似然函数）
  • 标签问题则可有分量为 1

• 适合场合

  • 多分类问题
  • 标签问题

Hinge Loss

• $y \in {-1, +1}$

• 合页损失函数：0-1 损失函数的上界，效果类似交叉熵损失函数

  • 要求分类不仅正确，还要求确信度足够高损失才为 0
  • 即对学习有更高的要求

• 适用场合

  • 二分类：线性支持向量机

收敛速度对比

• 指数激活函数时：相较于二次损失，收敛速度更快

• 二次损失对 $w$ 偏导

  $$\frac {\partial L} {\partial w} = (\sigma(z) - y) \sigma^{'}(z) x$$

  • $\sigma$：sigmoid、softmax 激活函数
  • $z = wx + b$

  • 考虑到 sigmoid 函数输入值绝对值较大时，其导数较小
  • 激活函数输入 $z=wx+b$ 较大时，$\sigma^{‘}(z)$ 较小，更新速率较慢

• Softmax 激活函数时，交叉熵对 $w$ 偏导

  $$\begin{align*} \frac {\partial L} {\partial w} & = -y\frac 1 {\sigma(z)} \sigma^{'}(z) x \\ & = y(\sigma(z) - 1)x \end{align*}$$

• 特别的，对 sigmoid 二分类

  $$\begin{align*} \frac {\partial L} {\partial w_j} & = -(\frac y {\sigma(z)} - \frac {(1-y)} {1-\sigma(z)}) \sigma^{'}(z) x \\ & = -\frac {\sigma^{'}(z) x} {\sigma(z)(1-\sigma(z))} (\sigma(z) - y) \\ & = x(\sigma(z) - y) \end{align*}$$
  • 考虑 $y \in {(0,1), (1,0)}$、$w$ 有两组
  • 带入一般形式多分类也可以得到二分类结果

不常用损失函数

Absolute Loss

绝对损失函数

• 适用场合
  • 回归预测

Logarithmic Loss

对数损失函数（负对数极大似然损失函数）

• 适用场合
  • 多分类：贝叶斯生成模型、逻辑回归

Exponential Loss

指数函数函数

• 适用场合
  • 二分类：前向分步算法

Pseudo Loss

伪损失：考虑个体损失 $(x_i, y_i)$ 如下，据此构造伪损失

• $h(x_i, y_i)=1, \sum h(x_i, y)=0$：完全正确预测
• $h(x_i, y_i)=0, \sum h(x_i, y)=1$：完全错误预测
• $h(x_i, y_i)=1/M$：随机预测（M为分类数目）

• $w_j$：样本个体错误标签权重，对不同个体分布可不同
• $f(x, y^{(j)})$：分类器将输入 $x$ 预测为第 $j$ 类 $y^{(j)}$ 的置信度

• 伪损失函数考虑了预测 标签 的权重分布

  • 通过改变此分布，能够更明确的关注难以预测的个体标签，而不仅仅个体

• 伪损失随着分类器预测准确率增加而减小

  • 分类器 $f$ 对所有可能类别输出置信度相同时，伪损失最大达到 0.5，此时就是随机预测
  • 伪损失大于 0.5 时，应该将使用 $1-f$

• 适用场景

  • 多分类：Adaboost.M2

Convolutional

卷积：卷积区域逐点乘积、求和作为卷积中心取值

• 用途：

  • 提取更高层次的特征，对图像作局部变换、但保留局部特征
  • 选择和其类似信号、过滤掉其他信号、探测局部是否有相应模式，如
    • sobel 算子获取图像边缘

• 可变卷积核与传统卷积核区别

  • 传统卷积核参数人为确定，用于提取确定的信息
  • 可变卷积核通过训练学习参数，以得到效果更好卷积核

• 卷积类似向量内积

特点

• 局部感知：卷积核所覆盖的像素只是小部分、局部特征

  • 类似于生物视觉中的 receptive field

• 多核卷核：卷积核代表、提取某特征，多各卷积核获取不同特征

• 权值共享：给定通道、卷积核，共用滤波器参数

  • 卷积层的参数取决于：卷积核、通道数
  • 参数量远小于全连接神经网络

• receptive field：感受野，视觉皮层中对视野小区域单独反应的神经元

  • 相邻细胞具有相似和重叠的感受野
  • 感受野大小、位置在皮层之间系统地变化，形成完整的视觉空间图

发展历程

• 1980 年 neocognitron 新认知机提出
  • 第一个初始卷积神经网络，是感受野感念在人工神经网络首次应用
  • 将视觉模式分解成许多子模式（特征），然后进入分层递阶式的特征平面处理

卷积应用

Guassian Convolutional Kernel

高斯卷积核：是实现 尺度变换 的唯一线性核

• $G(x,y,\sigma)$：尺度可变高斯函数
• $I(x,y)$：放缩比例，保证卷积核中各点权重和为 1
• $(x,y)$：卷积核中各点空间坐标
• $\sigma$：尺度变化参数，越大图像的越平滑、尺度越粗糙

Attention Machanism

注意力机制：将query、key-value映射至输出的权重生成机制

• $V_{L d_v}$：value矩阵，*信息序列矩阵
• $K_{L * d_k}$：key矩阵，大部分情况即为$V$
• $Q_{L * d_k}$：query矩阵，其他环境信息
• $L, d_k, d_v$：输入序列长度、key向量维度、value向量维度
• key、value向量为$K, V$中行向量

• 合理分配注意力，优化输入信息来源

  • 给重要特征分配较大权
  • 不重要、噪声分配较小权

• 在不同模型间学习对齐

  • attention机制常联合Seq2Seq结构使用，通过隐状态对齐
  • 如：图像至行为、翻译

Attention Model

• Attenion机制一般可以细化如下

• $c_t$：context vector，注意力机制输出上下文向量
• $e_{t,j}$：$t$时刻$i$标记向量注意力得分
• $\alpha_{t,i}$：$t$时刻$i$标记向量注意力权重
• softmax归一化注意力得分

• $f_{Att}$：计算各标记向量注意力得分

  • additive attention
  • multiplicative/dot-product attention：
  • local attention

  • 其参数需联合整个模型训练、输入取决于具体场景

• $\phi_{Att}$：根据标记向量注意力权重计算输出上下文向量

  • stochastic hard attention
  • deterministic soft attention

• $Q$可能包括很多信息

  • Decoder结构输出、Encoder结构输入
  • $W$待训练权重矩阵
  • LSTM、RNN等结构隐状态

Additive Attention

• 单隐层前馈网络（MLP）

  $$e_{t,j} = v_a^T f_{act}(W_a [h_{t-1}; g_j])$$

  • $h_{t-1}$：输出结构隐状态
  • $g_j$：输入结构隐状态
  • $W_a, v_a$：待训练参数
  • $f_{act}$：激活函数$tanh$、$ReLU$等

Multiplicative/Dot-product Attention

• 相较于加法attention实际应用中更快、空间效率更高 （可以利用高度优化的矩阵乘法运算）

• MLP
• 內积形式

Tricks

• 将输出作为输入引入，考虑上一次输出影响

  

• Scaled Dot-Product Attention

  $$f_{Att} = \frac {Q K^T} {\sqrt{d_k}}$$
  • 避免內积随着key向量维度$d_k$增大而增大，导致softmax 中梯度过小

Stochastic Hard Attention

hard attention：随机抽取标记向量作为注意力位置

• 注意力位置视为中间one-hot隐向量，每次只关注某个标记向量

• 模型说明

  • $f_{Att}$为随机从标记向量$a$中抽取一个
  • $\alpha$视为多元伯努利分布参数，各分量取值表示对应 标记向量被抽中概率，此时上下文向量也为随机变量

• $s$：注意力位置，中间隐one-hot向量，服从$\alpha$指定的 多元伯努利分布
• $h_i$：第$i$上下文向量

参数训练

• 参数$\alpha$不可导、含有中间隐变量$s$，考虑使用EM算法 思想求解

  $$\begin{align*} log p(y) & = log \sum_s p(s) p(y|s) \\ & \geq \sum_s p(s) log p(y|s) := L_s \\ \frac {\partial L_s} {\partial W} & = \sum_s [ \frac {\partial p(s)} {\partial W} + \frac 1 {p(y|s)} \frac {\partial p(y|s)} {\partial W}] \\ & = \sum_s p(s) [\frac {\partial log p(y|s)} {\partial W} + log p(y|s) \frac {\partial log p(s|a)} {\partial W}] \end{align*}$$

  • $L_s$：原对数似然的函数的下界，以其作为新优化目标
  • $W$：参数

• 用蒙特卡罗采样方法近似求以上偏导

  • $s$按多元伯努利分布抽样$N$次，求$N$次偏导均值

    $$\frac {\partial L_s} {W} \approx \frac 1 N \sum_{n=1}^N [\frac {\partial log p(y|\tilde s_n)} {\partial W} + log p(y|\tilde s_n) \frac {\partial log p(\tilde s_n|a)} {\partial W}]$$

    • $\tilde s_n$：第$n$次抽样结果

  • 可对$p(y|\tilde s_n)$进行指数平滑减小估计方差

Deterministic Soft Attention

soft attention：从标记向量估计上下文向量期望

• 考虑到所有上下文向量，所有标记向量加权求和上下文向量
• 模型说明
  • $f_{Att}$计算所有标记向量注意力得分
  • $\alpha$可视为个标记向量权重

• 模型光滑可微：可直接用反向传播算法训练

Local Attention

local attention：从所有标记向量中选取部分计算soft attention

• 可以视为hard、soft attention结合
  • hard attention选取标记向量子区间，避免噪声干扰
  • soft attention加权求和，方便训练

子区间选取

• 为目标$t$选取对齐位置$p_t$，得到子区间$[p_t-D, p_t+D]$ （$D$为经验选取）

• monotonic alignment：直接设置$p_t=t$

• predictive alignment：

  $$p_t = S sigmoid(v_p^T tanh(W_p h_t))$$

  • $W_p, v_p$：待学习参数

• 可以使用高斯分布给注意力权重加权，强化$p_t$附近标记向量 （根据经验可以设置$\sigma = \frac D 2$） $$\alpha_{t,j} = softmax(e_{t,j}) exp(-\frac {(j - p_t)^2} {2\sigma^2})$$

Self Attention

Self Attention/Intra-Attention：关联同一序列内不同位置、 以学习序列表示的attenion机制

• 类似卷积、循环结构

  • 将不定长的序列映射为等长的另一序列
  • 从序列中提取高层特征

• 特点

  • 类似卷积核，多个self attention可以完全并行
  • 无需循环网络多期传递信息，输入序列同期被处理
  • 可使用local attention机制限制计算复杂度

Multi-Head Attention

Multi-Head Attention：从相同输入、输出序列学习多个 attention机制

• $Q, K, V$：元信息矩阵，据此训练多组query、key-value， 一般就是原始输入序列矩阵

• 可以并行训练，同时从序列中提取多组特征

人工交互作用层

交互作用层：人工设置特征之间交互方式

Flatten Layer

展平层：直接拼接特征，交互作用交由之后网络训练

• $V_x$：特征向量集合

• 对同特征域特征处理方式
  • 平均
  • 最大

二阶交互作用

二阶交互作用层：特征向量之间两两逐元素交互

• 交互方式
  • 逐元素
    • 乘积
    • 求最大值：无
  • 按向量
• 聚合方式
  • 求和
    • 平权
    • Attention加权
  • 求最大值：无

Bi-Interaction Layer

Bi-Interaction Layer：特征向量两两之间逐元素乘积、求和

• $\odot$：逐元素乘积

• 没有引入额外参数，可在线性时间$\in O(kM_x)$内计算
• 可在低层次捕获二阶交互影响，较拼接操作更informative
  • 方便学习更高阶特征交互
  • 模型实际中更容易训练

Attention-based Pooling

Attention-based Pooling：特征向量两两之间逐元素乘积、加权 求和

• $\alpha_{i,j}$：交互作用注意力权重，通过注意力网络训练

Embedding

嵌入层：将高维空间中离散变量映射为低维稠密 embedding 向量表示

• embedding 向量更能体现样本之间关联

  • 內积（內积）体现样本之间接近程度
  • 可通过可视化方法体现样本差异

• embedding 向量更适合某些模型训练

  • 模型不适合高维稀疏向量
  • embedding 向量矩阵可以联合模型整体训练，相当于提取特征
  • embedding 向量也可能类似迁移学习独立训练之后直接融入模型中

• Embedding：将度量空间中对象映射到另个（低维）度量空间，并尽可能保持不同对象之间拓扑关系，如 Word-Embedding

Embedding表示

• 特征不分组表示

  $$\begin{align*} \varepsilon_x & = E x \\ & = [x_1v_1, x_2v_2, \cdots, x_Mv_M] \\ & = [x_{M_1} v_{M_1}, \cdots, x_{M_m} v_{M_m}] \end{align*}$$

  • $E$：embedding向量矩阵
  • $M$：特征数量
  • $v_i$：$k$维embedding向量
  • $x_i$：特征取值，对0/1特征仍等价于查表，只需考虑非0特征

    • $x_{M_i}$：第$j$个非0特征，编号为$M_i$
    • $m$：非零特征数量

  • $\varepsilon_x$：特征向量集合

• 特征分组表示

  $$\begin{align*} \varepsilon_x & = [V_1 g_1, V_2 g_2, \cdots, V_G g_G] \end{align*}$$

  • $G$：特征组数量
  • $V_i$：第$i$特征组特征向量矩阵
  • $g_i$：第$i$特征组特征取值向量

池化/下采样

池化：在每个区域中选择只保留一个值

• 用于减小数据处理量同时保留有用的信息

  • 相邻区域特征类似，单个值能表征特征、同时减少数据量

• 保留值得选择有多种

  • 极值
  • 平均值
  • 全局最大

• 直观上

  • 模糊图像，丢掉一些不重要的细节

Max Pooling

最大值采样：使用区域中最大值作为代表

Average Pooling

平均值采样：使用池中平均值作为代表

Recurrent Neural Network

RNN：处理前后数据有关联的序列数据

• 左侧：为折叠的神经网络，右侧：按时序展开后的网络
• $h$：循环隐层，其中神经元之间有权连接，随序列输入上一期 隐层会影响下一期
• $o$、$y$：输出预测值、实际值
• $L$：损失函数，随着时间累加

• 序列往往长短不一，难以拆分为独立样本通过普通DNN训练

结构

• 普通的DNN：固定大小输入得到固定输出
• 单个输入、序列输出：输入图片，得到描述文字序列
• 序列输入、单个输出：情感分析
• 异步序列输入、输出：机器翻译
• 同步序列输入、输出：视频帧分类

权值连接

• 循环隐层内神经元之间也建立权连接，即循环

  • 基础神经网络只在层与层之间建立权值连接是RNN同普通DNN 最大不同之处

• 循环隐层中神经元只会和其当前层中神经元建立权值连接

  • 即不受上期非同层神经元影响
  • 循环隐层中神经元$t$期状态$h^{(t)}$由当期输入、 $h^{(t-1)}$共同决定

• Gated Feedback RNN：循环隐层会对下期其他隐层产生影响

逻辑结构

• RNN网络实际结构是线性、折叠的，逻辑结构则是展开的结构， 考虑RNN性质应该在展开的逻辑结构中考虑

• 序列输入

  • 实际结构：依次输入
  • 逻辑结构：里是整体作为一次输入、才是一个样本，损失、 反向传播都应该以完整序列为间隔

• 权值共享

  • 实际结构：不同期的权值实际是同一组
  • 逻辑结构：称为权值共享

• 重复模块链

  • 实际结构：同一个模块
  • 逻辑结构：不同期模块之间信息流动形成链式形式

信息传递

• RNN循环层中信息只能由上一期直接传递给下一期

• 输入、输出相关信息间隔较近时，普通RNN可以胜任

  

• 当间隔很长，RNN理论上虽然能够处理，但由于梯度消失问题， 实际上长期依赖会消失，需要LSTM网络

  

Forward Propogation

• $h^{(t)} = \sigma(z^{(t)}) = \sigma(Ux^{(t)} + Wh^{(t-1)} +b )$

  • $\sigma$：RNN激活函数，一般为$tanh$
  • $b$：循环隐层偏置

• $o^{(t)} = Vh^{(t)} + c$

  • $c$：输出层偏置

• $\hat{y}^{(t)} = \sigma(o^{(t)})$

  • $\sigma$：RNN激活函数，分类时一般时$softmax$

Back-Propogation Through Time

BPTT：训练RNN的常用方法

• 本质仍然是BP算法，但是RNN处理序列数据，损失随期数累加， 即计算梯度时使用最终损失$L = \sum_{t=1}^\tau L^{(t)}$

• 对循环层中参数，梯度沿着期数反向传播，第t期反向传播时， 需要逐级求导

• 序列整体作为一次输入，进行一次反向传播
• 理论上可以漂亮的解决序列数据的训练，但是和DNN一样有梯度 消失的问题，尤其是序列很长时，所以一般不能直接应用

非循环层

• $\frac{\partial L}{\partial c}$

  $$\begin{align*} \frac{\partial L}{\partial c} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}}{\partial c} & = \sum_{t=1}^{\tau}\frac{\partial L^{(t)}} {\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} & = \sum_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)} \end{align*}$$

  • $L^{(t)} = \frac 1 2 (\hat{y}^{(t)} - y^{(t)})^2$： 使用平方损失

• $\frac{\partial L}{\partial V}$

  $$\begin{align*} \frac{\partial L}{\partial V} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}}{\partial V} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}} {\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial V} & = \sum_{t=1}^{\tau}(\hat{y}^{(t)} - y^{(t)}) (h^{(t)})^T \end{align*}$$

循环层

• 为方便定义： $\delta^{(t)} = \frac {\partial L} {\partial h^{(t)}}$

• $\delta^{(t)}$

  $$\begin{align*} \delta^{(t)} & = \frac {\partial L} {\partial h^{(t)}} \\ & = \frac{\partial L}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial h^{(t+1)}} \frac{\partial h^{(t+1)}}{\partial h^{(t)}} & = V^T(\hat{y}^{(t)} - y^{(t)}) + W^T\delta^{(t+1)}diag(1-h^{(t+1)})^2) \end{align*}$$

  • $\frac{\partial h^{(t+1)}}{\partial h^{(t)}} = diag(1-h^{(t+1)})^2)$ ：$tanh(x)$梯度性质
  • $h^{(t)}(t<\tau)$梯度：被后一期影响（反向传播），需递推

• $\delta^{(\tau)}$

  $$\begin{align*} \delta^{(\tau)} & = \frac{\partial L}{\partial o^{(\tau)}} \frac{\partial o^{(\tau)}}{\partial h^{(\tau)}} & = V^T(\hat{y}^{(\tau)} - y^{(\tau)}) \end{align*}$$

  • $\tau$期后没有其他序列，可以直接求出

• $\frac{\partial L}{\partial W}$

  $$\begin{align*} \frac{\partial L}{\partial W} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial W} & = \sum_{t=1}^{\tau}diag(1-(h^{(t)})^2) \delta^{(t)}(h^{(t-1)})^T \end{align*}$$

  • 需要由$\sigma^{(t)}$累加得到

• $\frac{\partial L}{\partial b}$

  $$\begin{align*} \frac{\partial L}{\partial b} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial b} & = \sum_{t=1}^{\tau} diag(1-(h^{(t)})^2)\delta^{(t)} \end{align*}$$

• $\frac{\partial L}{\partial U}$

  $$\begin{align*} \frac{\partial L}{\partial U} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial U} & = \sum_{t=1}^{\tau}diag(1-(h^{(t)})^2) \delta^{(t)}(x^{(t)})^T \end{align*}$$

}$$