Recurrent Neural Network

Recurrent Neural Network

RNN：处理前后数据有关联的序列数据

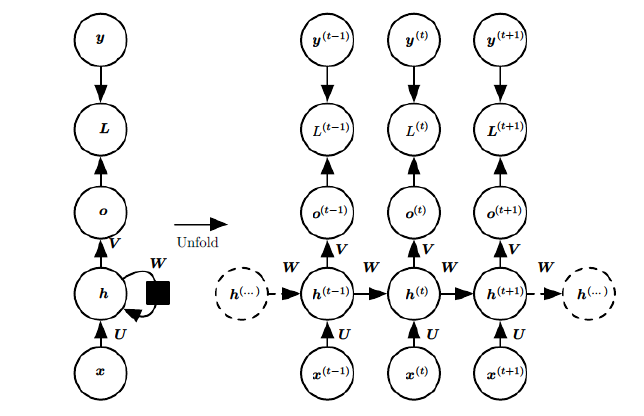
• 左侧：为折叠的神经网络，右侧：按时序展开后的网络
• $h$：循环隐层，其中神经元之间有权连接，随序列输入上一期 隐层会影响下一期
• $o$、$y$：输出预测值、实际值
• $L$：损失函数，随着时间累加

• 序列往往长短不一，难以拆分为独立样本通过普通DNN训练

结构

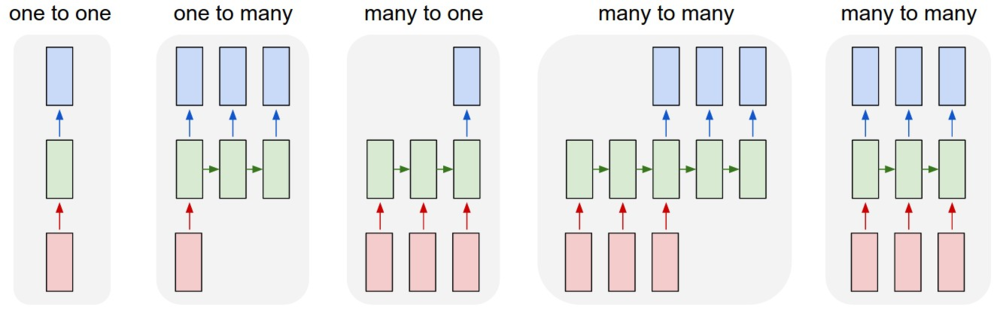
• 普通的DNN：固定大小输入得到固定输出
• 单个输入、序列输出：输入图片，得到描述文字序列
• 序列输入、单个输出：情感分析
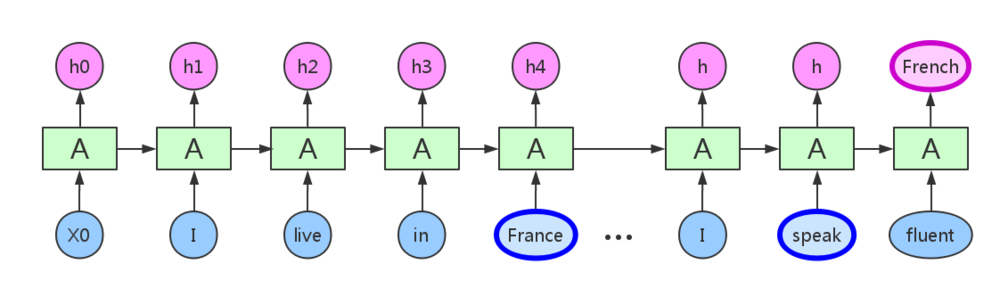
• 异步序列输入、输出：机器翻译
• 同步序列输入、输出：视频帧分类

权值连接

• 循环隐层内神经元之间也建立权连接，即循环

  • 基础神经网络只在层与层之间建立权值连接是RNN同普通DNN 最大不同之处

• 循环隐层中神经元只会和其当前层中神经元建立权值连接

  • 即不受上期非同层神经元影响
  • 循环隐层中神经元$t$期状态$h^{(t)}$由当期输入、 $h^{(t-1)}$共同决定

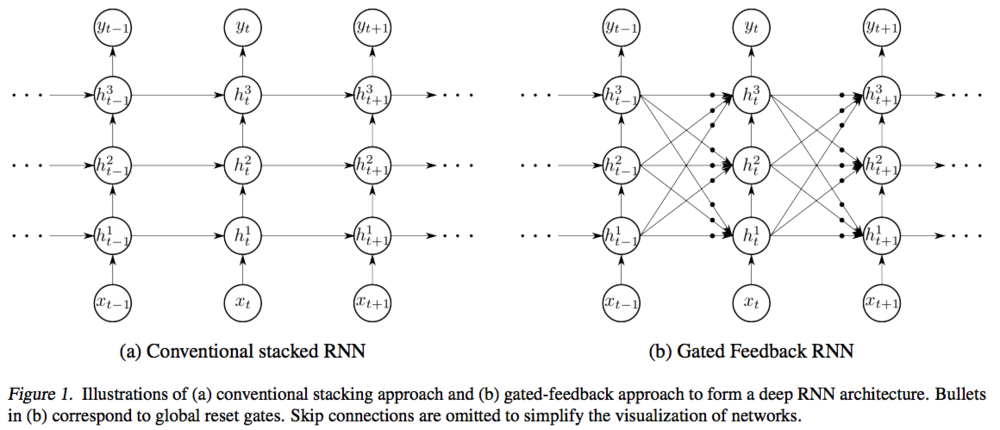
• Gated Feedback RNN：循环隐层会对下期其他隐层产生影响

逻辑结构

• RNN网络实际结构是线性、折叠的，逻辑结构则是展开的结构， 考虑RNN性质应该在展开的逻辑结构中考虑

• 序列输入

  • 实际结构：依次输入
  • 逻辑结构：里是整体作为一次输入、才是一个样本，损失、 反向传播都应该以完整序列为间隔

• 权值共享

  • 实际结构：不同期的权值实际是同一组
  • 逻辑结构：称为权值共享

• 重复模块链

  • 实际结构：同一个模块
  • 逻辑结构：不同期模块之间信息流动形成链式形式

信息传递

• RNN循环层中信息只能由上一期直接传递给下一期

• 输入、输出相关信息间隔较近时，普通RNN可以胜任

  

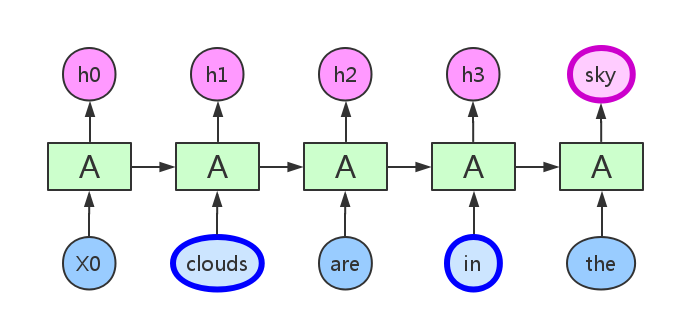
• 当间隔很长，RNN理论上虽然能够处理，但由于梯度消失问题， 实际上长期依赖会消失，需要LSTM网络

  

Forward Propogation

• $h^{(t)} = \sigma(z^{(t)}) = \sigma(Ux^{(t)} + Wh^{(t-1)} +b )$

  • $\sigma$：RNN激活函数，一般为$tanh$
  • $b$：循环隐层偏置

• $o^{(t)} = Vh^{(t)} + c$

  • $c$：输出层偏置

• $\hat{y}^{(t)} = \sigma(o^{(t)})$

  • $\sigma$：RNN激活函数，分类时一般时$softmax$

Back-Propogation Through Time

BPTT：训练RNN的常用方法

• 本质仍然是BP算法，但是RNN处理序列数据，损失随期数累加， 即计算梯度时使用最终损失$L = \sum_{t=1}^\tau L^{(t)}$

• 对循环层中参数，梯度沿着期数反向传播，第t期反向传播时， 需要逐级求导

• 序列整体作为一次输入，进行一次反向传播
• 理论上可以漂亮的解决序列数据的训练，但是和DNN一样有梯度 消失的问题，尤其是序列很长时，所以一般不能直接应用

非循环层

• $\frac{\partial L}{\partial c}$

  $$\begin{align*} \frac{\partial L}{\partial c} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}}{\partial c} & = \sum_{t=1}^{\tau}\frac{\partial L^{(t)}} {\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} & = \sum_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)} \end{align*}$$

  • $L^{(t)} = \frac 1 2 (\hat{y}^{(t)} - y^{(t)})^2$： 使用平方损失

• $\frac{\partial L}{\partial V}$

  $$\begin{align*} \frac{\partial L}{\partial V} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}}{\partial V} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}} {\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial V} & = \sum_{t=1}^{\tau}(\hat{y}^{(t)} - y^{(t)}) (h^{(t)})^T \end{align*}$$

循环层

• 为方便定义： $\delta^{(t)} = \frac {\partial L} {\partial h^{(t)}}$

• $\delta^{(t)}$

  $$\begin{align*} \delta^{(t)} & = \frac {\partial L} {\partial h^{(t)}} \\ & = \frac{\partial L}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial h^{(t+1)}} \frac{\partial h^{(t+1)}}{\partial h^{(t)}} & = V^T(\hat{y}^{(t)} - y^{(t)}) + W^T\delta^{(t+1)}diag(1-h^{(t+1)})^2) \end{align*}$$

  • $\frac{\partial h^{(t+1)}}{\partial h^{(t)}} = diag(1-h^{(t+1)})^2)$ ：$tanh(x)$梯度性质
  • $h^{(t)}(t<\tau)$梯度：被后一期影响（反向传播），需递推

• $\delta^{(\tau)}$

  $$\begin{align*} \delta^{(\tau)} & = \frac{\partial L}{\partial o^{(\tau)}} \frac{\partial o^{(\tau)}}{\partial h^{(\tau)}} & = V^T(\hat{y}^{(\tau)} - y^{(\tau)}) \end{align*}$$

  • $\tau$期后没有其他序列，可以直接求出

• $\frac{\partial L}{\partial W}$

  $$\begin{align*} \frac{\partial L}{\partial W} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial W} & = \sum_{t=1}^{\tau}diag(1-(h^{(t)})^2) \delta^{(t)}(h^{(t-1)})^T \end{align*}$$

  • 需要由$\sigma^{(t)}$累加得到

• $\frac{\partial L}{\partial b}$

  $$\begin{align*} \frac{\partial L}{\partial b} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial b} & = \sum_{t=1}^{\tau} diag(1-(h^{(t)})^2)\delta^{(t)} \end{align*}$$

• $\frac{\partial L}{\partial U}$

  $$\begin{align*} \frac{\partial L}{\partial U} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial U} & = \sum_{t=1}^{\tau}diag(1-(h^{(t)})^2) \delta^{(t)}(x^{(t)})^T \end{align*}$$

}$$