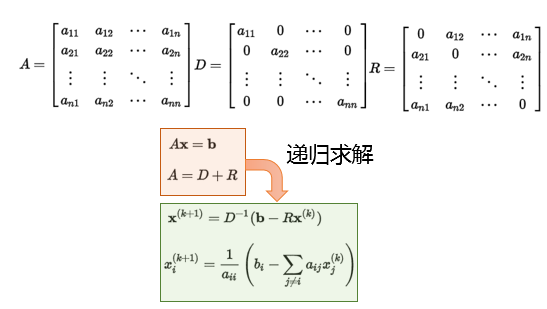
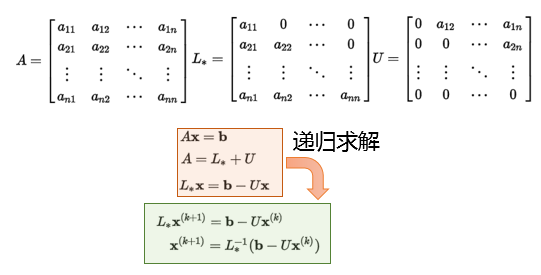
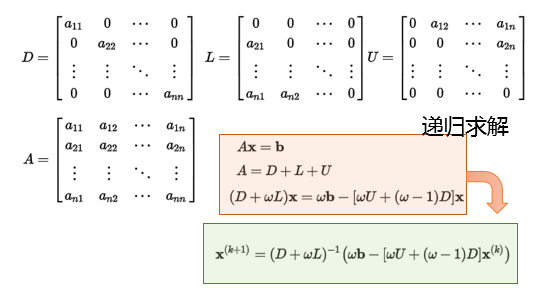
线性最长问题
最长公共子串
求两个字符串s1、s2(长度分别为m、n)最长公共子串长度
矩阵比较
将两个字符串分别以行、列组成矩阵M
对矩阵中每个元素$M[i, j]$,若对应行、列字符相同
元素置为1,否则置0
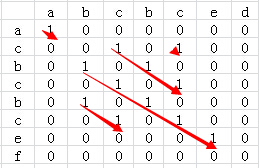
置元素$M[i,j] = M[i-1, j-1] + 1$,否则置0
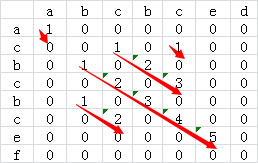
则矩阵中最长的非0斜序列对应子串即为最长公共子串
算法特点
- 时间效率$\in \Theta(mn)$
- 输入增强
最长公共子序列
求两个序列X、Y的最长公共子序列
- 子序列:去掉给定序列中部分元素,子序列中元素在原始序列中 不必相邻
- 最长公共子序列可能有很多
动态规划
先使用动态规划确认最长子序列长度,构造动态规划表
- $C[i,j]$:序列X前i个元素子序列、序列Y前j个元素子序列 最大子序列长度
根据动态规划表找出最长公共子序列
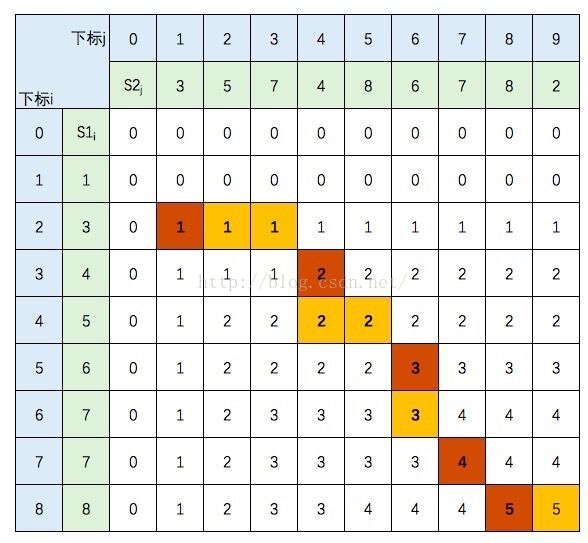
- 从动态规划表中首个格子开始,沿着某条格子路径达到 表中最后一个元素
- 路径中值改变格子对应序列中元素即为最长公共子序列中 元素
- 不同格子路径可能找到不同的最长公共子序列
算法特点
时间效率
- 动态规划部分$\in \Theta(|X||Y|)$
- 生成公共子序列部分$\in Theta(|X|+|Y|)$
动态规划
最长升/降序序列
寻找长度为N的序列L中最长单调自增子序列
最长公共子序列法
- 将原序列升序排序后得到$L^{ * }$
- 原问题转换为求$L, L^{ * }$最长公共子序列
算法特点
- 时间效率:$\in \Theta(|L|^2)$
动态规划法
使用动态规划法求出以$L[i]$结尾的最长升序子序列长度, 得到动态规划表
- $C[i]$:以$L[i]$结尾的最长升序子序列长度
则动态规划表中值最大者即为最长升序序列长度
算法特点
- 时间效率$\in O(|L|^2)$
动态规划2
使用线性表记录当前能够找到的“最长上升子序列”
若当前元素大于列表最后(大)元素:显然push进线性表
- 则当前线性表长度就是当前子串中最长上升子序列
若当前元素不大于列表中最后元素
- 考虑其后还有元素,可能存在包含其的更长上升序列
- 使用其替换线性表中首个大于其的元素
- 隐式得到以当前元素为结尾的最长上升子序列:其及 其之前元素
- 更新包含其的上升子序列的要求:之后元素大于其
- 不影响已有最长上升子序列长度,且若之后出现更长上升 子序列,则线性表被逐渐替换
算法
1 | lengthOfLIS(nums[0..n-1]): |
动态规划+二分
最长回文子串
中心扩展法
遍历串,以当前元素为中心向两边扩展寻找以回文串
为能找到偶数长度回文串,可以在串各元素间填充空位
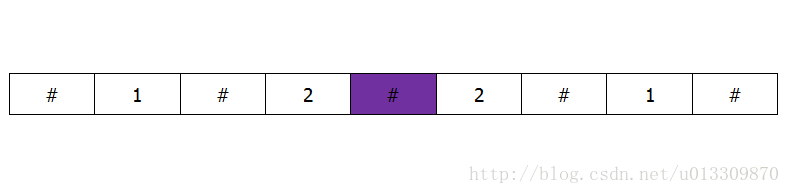
- 填充后元素位置$i = 2 i + 1$、填充符位置$2 i$
- 两端也要填充:否则可能出现
#为中心回文和端点回文 等长,但返回#中心回文 - 填充后得到最长回文串肯定是原最长回文串扩展
- 非
#中心:原串不存在偶数长度回文串更长,则显然 #中心:显然
- 非
算法
1 | LongestSubParlidrome(nums[0..n-1]): |
特点
- 算法效率
- 时间复杂度$\in O(n^2)$
- 空间复杂度$\in O(1)$
动态规划
Manacher算法
考虑已经得到的以$i$为中心、半径为$d$回文子串对称性
- 则$[i-d, i+d+1)$范围内中回文对称
- 即若$i-j, j<d$为半径为$dd$的回文串中心,则$2i - j$ 同样为半径为$dd$的回文串中心 ($[i-d, i+d-1)$范围内)
所以可以利用之前回文串信息减少之后回文串检测
- Manacher算法同样有中心扩展算法问题,要填充检测偶数长串
算法
1 | LongestSubParlidrome(nums[0..n-1]): |
特点
- 算法效率
- 时间复杂度$\in \Theta(n)$
- 空间复杂度$\in \Theta(n)$