Matrix Decomposition
矩阵分解
矩阵加法分解:将矩阵分解为三角阵、对角阵之和
- 常用于迭代求解线性方程组
矩阵乘法分解:将矩阵分解为三角镇、对角阵、正交阵之积
- 以下分解均在实数域上,扩展至复数域需同样将相应因子矩阵 扩充至复数域上定义
矩阵加法分解
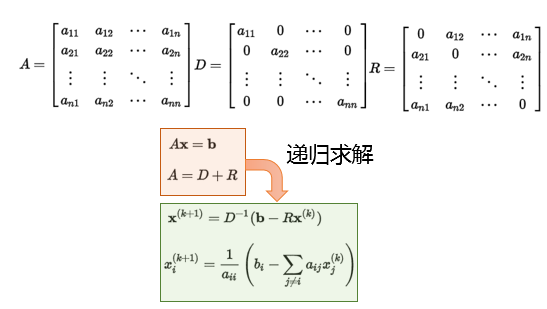
Jacobi分解
Jacobi分解:将矩阵分解为对角阵、非对角阵
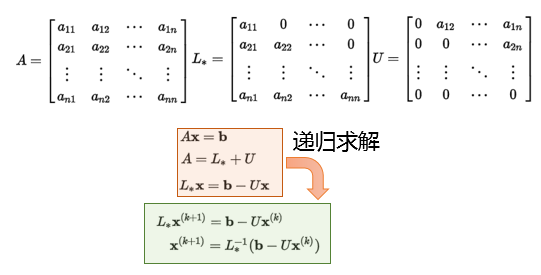
Gauss-Seidel分解
Gauss-Seidel分解:将矩阵分解为上、下三角矩阵
Successive Over Relaxation
SOR:逐次超松弛迭代法,分解为对角、上三角、上三角矩阵,同时 增加权重$w$调整分解后比例
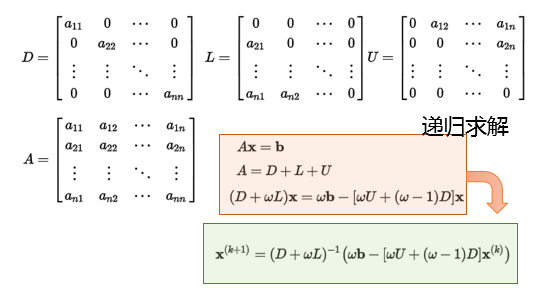
- 利用内在等式应用的平衡性、不动点收敛理论可以快速迭代
- $x$拆分到等式左右两侧,可以视为$y=x$和另外函数交点
- 根据不动点收敛理论可以进行迭代求解
LU系列分解
LU Decomposition
LU分解:将方阵分解为lower triangualr matrix、 upper triangluar matrix
- $L$:下三角矩阵
- $U$:上三角矩阵
- 特别的可以要求某个矩阵对角线元素为1
- 几何意义:由单位阵出发,经过竖直、水平切变
特点
LU分解实际上不需要额外存储空间,矩阵L、U可以合并存储
LU分解可以快速求解线性方程组,可以视为高斯消元法的矩阵 形式
得到矩阵LU分解后,对任意向量b,可使用已有LU分解 求解
- L为消元过程中的行系数和对角线全为1的下三角矩阵 (负系数在矩阵中为正值)
- U为消元结果上三角矩阵
则解方程组$Ax=b$等价于$LUx=b$
- 先求解$Ly=b$
- 再求解$Ux=x$
LDU Decomposition
LDU分解:将矩阵分解为下三角、上三角、对角矩阵
- LU分解可以方便的得到LDU分解:提取对角阵、然后对应矩阵 元素等比缩放
PLU[Q] Decomposition
- PLU分解:将方阵分解为置换矩阵、下三角、上三角矩阵
- PLUQ分解:将方阵分解为置换矩阵、下三角、上三角、置换矩阵
- 考虑$P^{-1}A=LU$,交换$A$行即可作普通LU分解,PLUQ分解 类似
- PLU分解数值稳定性好、实用工具
LL/Cholesky Decomposition
LL分解:将对称阵分解为下三角、转置
Cholesky分解常用于分解$A^TA$
- 常用于相关分析,分解相关系数阵、协方差阵
相较于一般LU分解,Cholesky分解速度更快、数值稳定性更好
- 类似的有LDL分解,同时提取对角线元素即可
Singular Value Decomposition
SVD奇异值分解:将矩阵分解为正交矩阵、对角矩阵、正交矩阵
- 特征值分解在任意矩阵上推广:相应的特征值、特征向量 被称为奇异值、奇异向量
- 几何意义:由单位阵出发,经旋转、缩放、再旋转
特点
$\Sigma$对角线元素为$M^T M$、$M M^T$的奇异值
- 可视为在输入输出间进行标量的放缩控制
- 同$U$、$V$的列向量相对应
$U$的列向量称为左奇异向量
- $M M^T$的特征向量
- 与$M$正交的“输入”或“分析”基向量
$V$的列向量成为右奇异向量
- $M^T M$的特征向量
- 与$M$正交的“输出”基向量
低阶近似
对$m * n$阶原始矩阵$M$
- 设其秩为$K \leq min(m, n)$,奇异值为 $d_1 \geq d_2 \geq \cdots \geq d_K > 0$
- 不失一般性可以设其均值为0
根据Eckart and Young的结果
- $u_k, v_k$:$U, V$的第$k$列向量
- $|M|_F$:矩阵的Frobenius范数
QR Decomposition
QR分解:将矩阵分解为正交矩阵、上三角矩阵
- 几何意义:由单位阵出发,经旋转、切变
特点
- 正交矩阵逆为其转置,同样可以方便求解线性方程组
Matrix Decomposition
https://xyy15926.github.io/Math-Algebra/Linear-Algebra/matrix_decomposition.html

