常用统计量
混淆矩阵
- 对比实际类别值、预测类别值,编制混淆矩阵
- 基于混淆矩阵,计算各类错判率、总错判率(总错判率会受到数据不平衡性的影响)
| 真实情况\预测结果 | 正例 | 反例 |
|---|---|---|
| 正例 | TP(真正例) | FN(假反例) |
| 反例 | FP(假正例) | TN(真反例) |
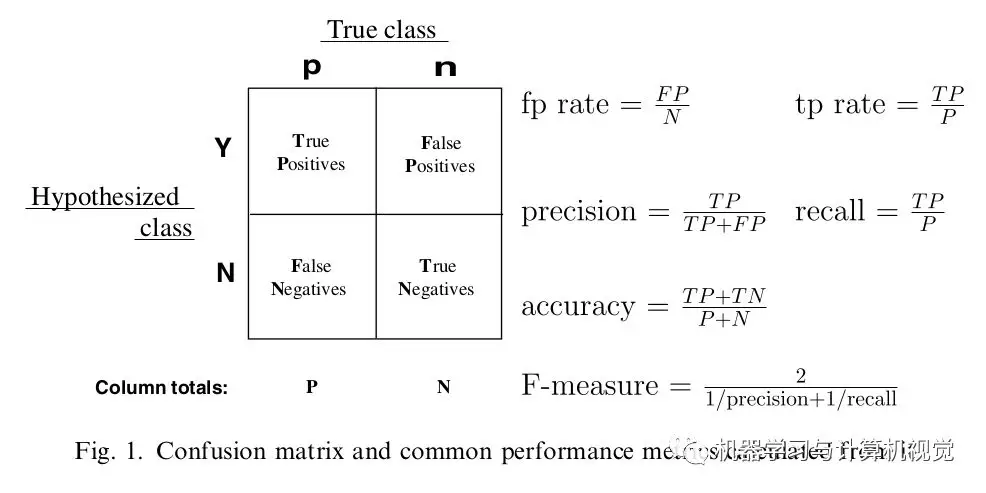
F-Measure
F-测度:准率率和召回率综合值,越大越好
- $P = \frac {TP} {TP+FP}$:查准率、精确率
- $R = \frac {TP} {TP+FN}$:查全率、召回率、覆盖率
F1 值
F1值:$\beta=1$ 时的 F测度
TPR、FPR
TPR、FPR 可视为对 TP、FP 用样本数量归一化的结果
- 样本全体中正、负样本数量往往差距很大,直接比较 TP、FP 不合理
- 考虑使用样本正、负数量归一化,即计算正比例 TPR、负比例 FPR
TPR 越高越好,FPR 越低越好,但是这两个指标相互制约,两者同时增加、减小
- 模型倾向于将样本 判定为 为正例,则 TP、FP 同时增加,TPR、FPR 同时变大
- 即模型取不同阈值,会产生正相关的 TPR、FPR 的点列
Recevier Operating Characteristic Curve
ROC 曲线:不同 正样本概率 划分阈值下 TPR、FPR 绘制的折线/曲线
ROC 曲线即以 FPR 为横坐标、TPR 为正坐标绘制曲线
- FPR 接近 1 时,TPR 也接近 1,这是不可避免的
- 而 FPR 接近 0 时,TPR 越大越好
- 所以模型 ROC 曲线下方面积越大,模型判断正确效果越好
理解
- 将正负样本的正样本概率值分别绘制在
x=1、x=-1两条直线上 - 阈值即为
y=threshold直线 - TPR、FPR 则为
x=1、x=-1两条直线在阈值直线上方点数量,与各直线上所有点数量比值
- 将正负样本的正样本概率值分别绘制在
Accuracy
准确率、误分率:评价分类器性能一般指标
- $y_i$:第 $i$ 样本实际类别
- $\hat y_i$:第 $i$ 样本预测类别
- $N$:样本数量
- 对给定测试集,分类器正确分类样本数与总样本数比值
- 即 0-1 损失函数时经验风险
Top PR
头部准召:评估模型头部性能
- $TOP$:指定的头部数量
- $TP_{top}$:头部中正例数量(正例指已知原 $TOP$ 样本)
Area Under Curve
AUC 值:ROC 曲线下方面积,越大越好
AUC 值实际含义:随机抽取一对正、负样本,对其中正样本的正样本预测概率值、大于负样本的正样本预测概率值的概率
- $=1$:完美预测,存在一个阈值可以让模型 TPR 为 1,FPR 为 0
- $(0.5, 1)$ :优于随机预测,至少存在某个阈值,模型 $TPR > FPR$
- $=0.5$:同随机预测,无价值
- $[0, 0.5)$:差于随机预测,但是可以反向取预测值
AUC 计算
绘制 ROC 曲线,计算曲线下面积
- 给定一系列阈值(最精确时为样本数量),分别计算 TPR、FPR
- 根据 TPR、FPR 计算 AUC
正负样本分别配对,计算正样本预测概率大于负样本比例
- $M, N$:正、负样本数量
Mann-Witney U 检验:即正、负样本分别配对的简化公式
- $Pos$:正样本集合
- $rank(i)$:样本 $i$ 的按正样本概率排序的秩(对正样本概率值相同样本,应将秩加和求平均保证其秩相等)
Weighted-AUC
WAUC:给 每个样本 赋权,计算统计量时考虑样本权重
FPR、TPR 绘图
- $WTPR, WFPR$:加权 TPR、加权 FPR
- $\hat y_i$:样本预测类别
- $w_i$:样本权重
Mann-Witney U 检验:考虑其意义,带入权重即可得
- $rank_{pos}(i)$:正样本内部排序,样本$i$秩
- $Neg$:负样本集合
多分类 AUC
Micro-AUC:将每个类别视为样本标签,计算全体样本的正标签、负标签的 AUC
- $n$ 个样本的 $m$ 维标签展平, 则其中有 $n$ 个正样本、$n * (m-1)$ 个负样本
- $n$ 个样本的 $m$ 个分类器共 $n * m$ 个得分展平
- 使用以上预测得分、标签计算 AUC
1
2
3
4
5
6
7
8
9
10# one-vs-rest分类器得分
y_score = classifer.transform(X_test)
# 展平后计算fpr、tpr
fpr_micro, tpr_micro, threshhold_micro = \
skilearn.metrics.roc_curve(y_test.ravel(), y_score.ravel())
# 利用fpr、tpr计算auc
auc_micro = skilearn.metrics.auc(fpr_micro, tpr_micro)
# 等价于直接调用
auc_micro = skilearn.metrics.roc_auc_score(y_test, y_score, average="micro")Macro-AUC:对各类别,分别以计算 ROC 曲线(即 TPR、FPR),计算平均 ROC 曲线得到 AUC
- 对各类别分别计算 TPR、FPR,共 $m$ 组 TPR、FPR
平均合并 TPR、FPR,计算 AUC
方法1:合并 FPR、去除重复值,使用 $m$ 组 TPR、FPR 分别求合并后 FPR 插值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16# 分别计算各类别fpr、tpr
fprs, tprs = [0] * n_classes, [0] * n_classes
for idx in range(n_classes):
fprs[idx], tprs[idx], _ = sklearn.metrics.ruc_curve(
y_test[:, i], y_score[:, i])
# 合并fpr
all_fpr = np.unique(np.concatenate(fprs))
mean_tpr = np.zeros_like(all_fpr)
# 计算合并后fpr插值
for idx in range(n_classes):
mean_tpr += scipy.interp(all_fpr, fpr[idx], tpr[idx])
mean_tpr /= n_classes
auc_macro = sklearn.metrics.auc(all_fpr, mean_tpr)
# 但是和以下结果不同
auc_macro = sklearn.metrics.roc_auc_score(fprs)
- 以上分类器均为 one-vs-rest 分类器,$m$ 个类别则 $m$ 个分类器、每个样本 $m$ 个得分
Kolmogorov-Smirnov 统计量
KS 值:刻画区分正负样本能力
- KS 值体现 最理想情况 下,对正负样本区分能力
- 即 ROC 曲线与 $TPR = FPR$ 直线的最远距离
Squared Error
Mean Squared Error
MSE:均方误差(偏差)
Mean Absolute Error
MAE:平均绝对误差
Mean Absolute Percentage Error
MAPE:平均绝对百分比误差
Symmetric Mean Absolute Percentage Error
SMAPE:对称平均绝对百分比误差
$R^2$
- $n, p$:样本量、特征数量
- $SSE$:残差平方和
- $SSR$:回归平方和、组内平方和
- $SST$:离差平方和
- $R^2_{adj}$:调整的$R^2$
Akaike Information Criterion
AIC :赤池信息准则
- $n, p$:样本量、特征数量
- $\theta$:带估参数
- $L(\theta, x)$:似然函数
- $SSE$:残差平方和
Bayesian Information Criterion
BIC:贝叶斯信息准则
$C_p$
- $p$:选模型特征子集中特征数量
- $m$:所有特征数量
- $SSE_p$:选模型中残差平方和
- $SSE_m$:全模型中残差平方和