Posted Updated Math Mixin / Time Seriesa minute read (About 207 words)

GARCH波动性建模

白噪声检验

进行ARIMA模型拟合时，通过检验查询序列是否通过LB检验（白噪声 检验）判断模型显著性，但是实际上

  • LB检验只检验了白噪声序列的纯随机性
  • 对于方差齐性没有进行检验
  • 至于零均值，可以在建模时通过拟合常数项解决

方差齐性变换

如果已知异方差函数的具体形式，找到其转换函数，进行方差齐性 变换

拟合条件异方差模型

Posted Updated RLanga minute read (About 181 words)

GGPLOT

GGPlot 绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
p <- ggplot(data=mtcars, aes(x=wt, y=mpg))

geom_bar(color, fill, alpha)
geom_histogram(color, fill, alpha, linetype, binwidth)
geom_boxplot(color, fill, alpha, notch, width)
geom_violin(color, fill, alpha, linetype)
geom_density(color, fill, alpha, linetype)

geom_rug(color, side)
geom_smooth(method, formula, color, fill, linetype, size)


geom_hline(color, alpha, linetype, size)
geom_gitter(color, size, alpha, shape)
geom_line(color, alpha, linetype, size)
geom_point(color, alpha, shape, size)
geom_vline(color, alpha, linetype, size)

geom_text()
  • color：点、线、填充区域着色
  • fill：对填充区域着色，如：条形、密度区域
  • alpha：颜色透明度，0~1逐渐不透明
  • linetype：图案线条
    • 1：实线
    • 2：虚线
    • 3：点
    • 4：点破折号
    • 5：长破折号
    • 6：双破折号
  • size：点尺寸、线宽度
  • shape：点形状
    • 1：开放的方形
Posted Updated RLang11 minutes read (About 1696 words)

R可视化

R图形参数

使用、保存图形

保存图形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
png(
	file= "Rplot%03d.png",
	width= 480,
	height= 480,
	units= "px",
		# 图片分辨率
	pointsize= 12,
		# 文字大小
	bg= "white",
	res= NA,
	family= "",
	restoreConsole= TRUE,
	type= c("windows", "cairo"),
	antialias
)
	# `par`语句生效必须放在`png`、`dev.off`中间
	# 这个语句会强制覆盖与`par`语句重合的部分参数，即使这个
		# 函数后调用

pdf(filename)
win.metafile(filename)
jpeg(filename)
bmp(filename)
tiff(filename)
xfig(filename)
postscript(filename)
	# 开启目标图形设备
dev.off()
	# 关闭目标图形设备
	# 绘图语句至于其中，包括`par`

dev.new()
	# 打开新的图形窗口，防止多次绘图覆盖
dev.next()
dev.prev()
dev.set()
	# 选择将图形发送到不同窗口

par

par函数设置对整个工作空间图像设置均有效

1
2
3
4
5
6
7
8
opar <- par()
	# 无参调用，生成含有当前图形参数设置的列表
opar <- par(no.readonly= TRUE)
	# 生成一个可以修改的当前图形参数列表
par(opar)
	# 恢复为`opar`中的参数设置
par(attr_name)
	# 获取某个属性设置值

符号、线条

1
2
3
4
5
6
7
8
9
10
par(
	pch= int,
		# 绘制点时使用的符号
	cex= num,
		# 符号大小，相对于默认大小缩放倍数
	lty= int,
		# 线条类型
	lwd= num,
		# 线条宽度，相对于默认线条宽度的倍数
)

颜色

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
par(
	col= str/c(str),
		# 绘图颜色，循环使用
	col.axis= str/c(str),
		# 坐标轴刻度文字颜色
	col.lab= str/c(str),
		# 坐标轴标签颜色
	col.main= str/c(str),
		# 标题颜色
	col.sub= str/c(str)
		# 副标题颜色
	fg= str/c(str),
		# 前景色
	bg= str/c(str),
		# 背景色
)

文本属性

1
2
3
4
5
6
7
8
9
10
11
12
par(
	cex= num,
		# 文本大小，相对默认
	cex.axis= num,
		# 坐标轴刻度文字的缩放倍数
	cex.lab= num,
		# 坐标轴标签缩放倍数
	cex.main= num,
		# 标题缩放倍数
	cex.sub= num,
		# 副标题缩放倍数
)

字体、字号、字样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
par(
	font= int,
		# 绘图使用字体样式
		# 1：常规、2：粗体、3：斜体、4：粗斜体
	font.axis= int,
		# 坐标轴刻度字体样式
	font.lab= int,
	font.main= int,
	font.sub= int,
	ps= num,
		# 字体磅值
		# 文本最终大小为`cex*ps`
	family= "serif"/"sans"/"mono"/str,
)

图形、边界尺寸

1
2
3
4
5
6
7
8
9
10
11
12
par(
	pin= c(width, height),
		# 图片尺寸，单位英寸
	mai= c(bot, left, top, right),
		# 边界大小，单位英寸
	mar= c(bot, left, top, right),
		# 边界大小，单位英分（1/12英寸）
		# 默认值`c(5, 4, 4, 2)+ 0.1`
	mgp= c(axis_labels, tick_title, tick),
		# 坐标轴标签、刻度标签、刻度线位置
		# 图形边缘为0，单位为行
)

文本、自定坐标、图例

title

title函数可以为图形添加标题、坐标轴标签

1
2
3
4
5
6
7
8
9
10
11
12
title(
	main= str,
	sub= str,
	xlab= str,
	ylab= str,

	col.main= str,
		# 也可以指定文本大小、字体、旋转角度、颜色
	col.sub= str,
	col.lab= str,
	cex.lab= str
)

axis

创建自定义坐标轴

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
axis(
	side= int,
		# 坐标轴位置
		# 1-4：下、左、上、右
	at= c(int),
		# 需要绘制刻度线的位置
	labels= c(str),	
		# 刻度线对应labels
		# 默认为`at`中值
	pos= num,
		# 坐标轴线绘制位置坐标，即与另一坐标轴交点
	lty= num,
		# 线条类型
	col= str,
		# 线条、刻度颜色
	las= 0/2,
		# 标签平行、垂直坐标轴
	tck= num,
		# 刻度线长度，相对于绘图区域大小分数表示
		# 负值表示在图形外侧
		# `0`表示禁用刻度线
		# `1`表示绘制网格线
		# 默认`-0.01`
)
minor.tick

次要刻度线

1
2
3
4
5
6
7
8
library(Hmisc)
minor.tick(
	nx= int,
		# x轴次要刻度**区间**数
	ny= int,
	tick.ratio= num
		# 次要刻度线相较主要刻度线比例
)

abline

添加参考线

1
2
3
4
5
6
7
abline(
	h= c(int),
		# 水平参考线位置（多根）
	v= c(int),
	lty= int,
	col= str,
)

legend

添加图例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
legend(
	location= c(x, y)/
		# 指定`x, y`坐标
		"bottom"/"bottomleft"/"left"/"topleft"/
		"top"/"topright"/"right"/"bottoright"/"center"/
		# 使用关键字指定图例位置
		locator(1),
		# 鼠标交互式指定
	inset= num,
		# `location`使用关键字指定位置，设置图例向图形内侧移动
		# 移动`num`绘图区域比例
	title= str,
		# 图例标题字符串
	legend= c(str),
		# 图例labels字符串向量
	col= c(col_str),
	pch= c(pch_int),
		# 若图例标识符号不同的点
	lwd= c(lwd_int),
	lty= c(lty_int),
		# 若图例标识宽度、样式不同的线
	fill= c(col_str),
		# 若图例标识颜色填充的盒型
)

mtext、text

  • mtext：向图形四个边界之一添加文本
  • text：向绘图区域内部添加文本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
text(
	location,
		# 同`legend`
	"text to place",
	pos= int,
		# 文本相对于`location`方向
		# 1-4：下、左、上、右
	offset= num,
		# 文本相对`location`偏移量
	cex= num,
	col= c(col_str),
	font= num,
)

mtext(
	"text to place",
	side= int,
		# 放置文本的边
		# 1-4：下、左、上、右
	line= num,
		# 向内、外移动文本
		# 越大文本越向外移动
	adj= int,
		# 1：文本坐下对齐
		# 2：文本右上对齐
	cex= num,
	col= c(col_str),
	font= num,
)

图形组合

par

1
2
3
4
5
6
7
8
9
10
11
12
13
14
par(
	mfrow= c(nrows, ncols)
)
	# 设置按行填充的图形矩阵
par(
	mfcol= c(nrows, ncols)
)
	# 设置按列填充的图形矩阵
	# 然后按照的绘图顺序依次填充矩阵

par(
	fig= c(x1, x2, y1, y2)
)
	# 接下来图形在`fig`指定范围内绘制

layout

1
2
3
4
5
6
7
8
9
10
layout(
	mat= matrix(int),
		# `mat`中元素值`n`表示第n个绘制的图形
		# 其在矩阵中所处的位置即其填充的位置
	widths= c(num),
		# 各列宽度值向量
		# 相对图形比例可以直接数值表示
		# 绝对数值可以通过函数`lcm`指定
	heights= c(num),
		# 各行高度值向量

R原始图表

条形图

1
2
3
4
5
6
7
8
barplot(
	H,
	xlab,
	ylab,
	main,
	names.arg,
	col
)

一般条形图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
H <- c(7, 12, 28, 3, 41)
M <- c("Mar", "Apr", "May", "Jun", "Jul")

png(file = "barchart.png")
	# 设置图表文件名
barplot(
	H,
		# 各组数据大小
	names.arg = M,
		# 各组labels
	xlab = "Month",
		# x轴名
	ylab = "Revenue",
		# y轴名
	col = "blue",
		# 条形填充颜色
	main = "Revenue Chart",
		# 标题
	border = "red"
		# 条形边框颜色
)
	# 绘制图表
dev.off()
	# 保存图表

组合、堆积条形图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
colors <- c("green", "orange", "brown")
months <- c("Mar", "Apr", "May", "Jun", "Jul")
regions <- c("East", "West", "North")

values <- matrix(
	c(2,9,3,11,9,4,8,7,3,12,5,2,8,10,11),
	nrow = 3,
	ncol = 5,
	byrow = TRUE)
png(file = "barchart_stacked.png")
barplot(
	values,
	main = "total revenue",
	names.arg = months,
	xlab = "month",
	ylab = "revenue",
	col = colors)

legend(
	"topleft",
	regions,
	cex = 1.3,
	fill = colors)

dev.off()

饼图

1
2
3
4
5
6
7
8
pie(
	x,
	labels,
	radius,
	main,
	col,
	clockwise
)

一般饼图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
piepercents <- round(100 * x / sum(x), 1)
	# `round`取小数位数

png(file = "city.png")
pie(
	x,
	labels = piepercents,
	main = "city pie chart",
	col = rainbow(length(x))
)

legend(
	"topright",
	labels,
		# 饼图注解设为百分比，所以这里设置各组别labels
	cex = 0.8,
	fill = rainbow(length(x))
)

dev.off()

3D饼图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
library(plotrix)
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")

png(file = "3d_pie_charts.jpg")

pie3D(
	x,
	labels,
	explode = 0.1
	main = "pie charts of countries"
)

dev.off()

直方图

1
2
3
4
5
6
7
8
9
10
11
hist(
	v,
	main,
	xlab,
	xlim,
	ylim,
	breaks,
		# 每个直方的宽度
	col,
	border
)

一般直方图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
v <- c(9,13,21,8,36,22,12,41,31,33,19)

png(file = "histogram.png")

hist(
	v,
	xlab = "weight",
	col = "green",
	border = "blue"
	xlim = c(0, 40),
	ylim = c(0, 5),
	breaks = 5
)

dev.off()
Posted Updated RLang21 minutes read (About 3158 words)

R语法

生存

配置

注释

  • R语言的注释和其他脚本语言类似，使用#注释行，但是R没有 多行注释语法
  • 可以使用if(FALSE)语句进行“注释”
    1
    2
    3
    if(FALSE) {
    	"comments"
    }

工作路径

1
2
3
4
getwd()
	# 返回当前工作路径，默认`~/Documents`
setwd(/path/to/dir)
	# 设置当前工作路径

变量

  • R中有效的变量名称由字母、数字、点、下划线组成，变量名以 字母、后不跟数字的点开头
  • R中变量为动态类型，可多次更改变量数据类型
  • 变量无法被声明，在首次赋值时生成

赋值

1
2
3
4
5
6
7
8
9
10
var.1 = c(0, 1, 2, 3)
	# 不常用
var.2 <- c("learn", "R")
	# 常用方法
var .3 <<- c(3, 1, TRUE, 2+3i)
	# 特殊赋值符，可以扩展变作用域为“整个”工作空间
	
c(TRUE, 1) -> var.4
	# 右赋值符
c(TRUE, 2+3i) ->> var.5

搜索

ls函数可以搜索当前工作空间中所有可用变量

1
2
3
4
5
6
ls(
	pattern = "var_pattern",
	all.name = FALSE/TRUE
)
	# `pattern`：使用模式匹配变量名
	# `all.name`：开头变量默认隐藏，可通过设置参数展示

删除

rm函数可以删除变量

1
2
3
4
rm(var.3)

rm(list = ls())
	# 删除所有变量

数据导入

edit

1
2
3
4
5
6
7
8
9
10
11
mydata <- data.frame(
	age = numeric(0),
	gender = character(0),
	weight = numeric(0)
)
	# `numeric(0)`类似的赋值语句创建指定模式但不含数据变量
mydata <- edit(mydata)
	# `edit`会调用允许手动输入数据的文本编辑其
	# `edit`在副本上操作，需要重新给变量
fix(mydata)
	# `mydata <- edit(mydata)`等价写法，直接在原对象上操作

read.table

1
2
3
4
5
6
7
8
9
10
11
12
13
DF <- read.table(
	file(/path/to/file),
	header = TRUE/FALSE,
	sep = " \t\n\r"/",",
	row.names = c(),
	col.names = c("V1", "V2", ...)/c(str),
	na.strings = NULL/c(str)),
	colClasses = NULL/c("numeric", "character", "NULL"),
	quote = "'""/str,
	skip = 0/int,
	stringAsFactors = TRUE/FALSE,
	test = str
)

  • 说明：从带分隔符的文本文件中导入数据

  • 参数

    • header：第一行是否包含变量名
    • sep：分隔符，默认数个空格、tab、回车、换行
    • row.names：指定行标记符
    • col.names：指定DF对象列名
    • na.strings：表示缺失值的字符串向量，其包含字符串 读取时转为NA
    • colClasses：设置DF对象每列数据模式
      • “NULL”表示跳过
      • 长度小于列数时开始循环
      • 读取大型文本可以提高速度
    • quote：字符串划定界限，默认"'
    • StringAsFactor：标记字符向量是否转换为factor
      • colClasses优先级更高
      • 设为FALSE可以提升读取速度
    • text：读取、处理的字符串，而不是file

常用函数

1
2
3
4
5
6
7
8
9
print()
	# 浏览对象取值
str()
	# 查看对象结构
ls()
	# 管理对象
remove()
rm()
	# 删除指定对象

数据模式（类型）

  • 数据模式是指R存储数据的方式
  • 即从存储角度对R数据对象划分
  • class函数就是返回数据模式（类型）

Logical

只需要1byte存储

  • TRUE/T
  • FALSE/F

Integer

占用2-4byte

  • 2L、0L

Numeric

可进一步分

  • float占用4byte
  • double占用8byte

R中数值型数据默认为double

  • 12.3、4

Complex

  • comlplex：3+2i

Character

R中'、"对中的任何值视为字符串

  • '、"必须在开头、结尾成对存在
  • '、"结尾的字符串中，只能插入对方

paste

连接多个字符串

1
2
3
4
5
6
7
Chars = paste(
	...,
		# 要组合的任意数量变量
	sep = " ",
		# 分隔符
	collapse = NULL)
		# 消除两个字符串之间空格

format

将数字、字符串格式为特定样式

1
2
3
4
5
6
7
8
9
10
11
12
13
Chars = format(
	x([num, chars],
		# 向量
	digits(int),
		# 显示的总位数
	nsmall(int),
		# 小数点右边最小位数
	scientific=FALSE/TRUE,
		# `TRUE`则显示科学计数法
	width(int),
		# 在开始处填充空白来显示的最小宽度
	justify = c("left", "right", "centre", "none"))
		# 字符串显示位置

nchar

计算包括空格在内的字符串长度

1
2
3
int = nchar(
	x(chars)
)

toupper、tolower

改变字符串大小写

1
2
3
4
5
6
chars = toupper(
	x(chars)
)
chars = tolower(
	x(chars)
)

substring

获取字符串子串

1
2
3
4
5
6
chars = substring(
	x(chars),
	first(int),
	last(int)
)
	# 包括头尾
  • R对象是指可以赋值给变量的任何事物，包括常量、数据结构、 函数
  • 对象都拥有某种模式，描述对象如何存储
  • 对象拥有某个“类”，向print这样的泛型函数表明如何处理 此对象

Raw

  • raw：v <- charToRaw("Hello")（byte类型）

结构角度划分R对象

Vector

用于存储数值型、字符型、逻辑型数据的一维数组

  • 单个向量中的出数据必须拥有相同的类型、模式（数值型、字符 型、逻辑型）
  • R中没有标量，标量以单元素向量形式出现
1
2
3
4
5
6
7
8
9
10
apple <- c("red", "green", "yellow") 
apple[1]
	# 访问单个元素，从1开始
apple[1: 3]
	# 切片，闭区间
apple[7] = "seven"
	# 将值赋给某个向量、矩阵、数组或列表中一个不存在的元素时
		# R将自动扩展其以容纳新值，中间部分设为`NA`

is.vector(apple)

创建向量

1
2
3
4
5
6
7
8
9
10
11
12
rep(start: end, each=repeat_time)
	# 元素重复
rep(start: end, times=repeat_time)
	# 向量重复

seq(from=start, to=end, by=step)
	# 指定步长
seq(from=start, to=end, length=len)
	# 指定个数

vector(length=len)
	# 元素为`FALSE`

访问向量元素

1
2
3
4
5
6
7
a[1]
a[1:2]
a[c(1,3)]
a[c(T, F, T)]

a[-c(1:2)]
	# 负号不能用于逻辑向量

Matrix

二维数组：组织具有相同存储类型的一组变量

  • 每个元素都拥有相同的模式（数值型、字符型、逻辑型）

创建矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
mtx <- matrix(
	vector,
	nrow(int)
	ncol(int),
	byrow = FALSE/TRUE,
	dimnames = list(
		c(row_names),
		c(col_names)
	)
)

is.matrix()

cbind()
	# 将多个已有向量（列）合并为矩阵

矩阵信息

1
2
3
4
5
6
dim(mtx)
	# 显示矩阵行、列
colnames(mtx)
colnames(mtx[, col_start: col_end])
rownames(mtx)
ronnames(mtx[row_start: row_end, ])

访问矩阵元素

1
2


Array

类似于矩阵，但是维度可以大于2

  • 其中元素也只能拥有一种模式
1
2
3
4
5
arr <- array(
	vector,
	dimensions(c(int)),
	dimnames = c(dim_names)
)

Data.Frame

数据帧是表、二维数组类似结构

  • 不同的列可以包含不同的模式
  • 每列包含一个变量的值，每行包含来自每列的一组值
  • 数据帧的数据可是数字、因子、字符串类型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
df <- data.frame(
	col1(c()),
	col2(c()),
	...,
	row.names = coln
)
	# `row.names`：指定实例标识符，即index

emp.data <- data.frame(
	emp_id = c(1:5),
	emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
	salary = c(623.3,515.2,611.0,729.0,843.25),
	start_date = as.Date(c("2017-01-01", "2017-09-23",
		"2017-11-15", "2017-05-11", "2018-03-27")),
	stringsAsFactors = FALSE
)
	# 创建DF

统计性质

1
2
3
4
5
str(emp.data)
	# 可以获得DF结构

summary(emp.data)
	# 获得DF的统计摘要、性质

筛、删、减

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
emp.data.cols <- data.frame(
	emp.data$emp_name,
	emp.data$salary)
	# 列名称获取DF中特定列

emp.data.rows <- emp.data([1:2, ]
	# 行切片获取特定行

emp.data.rows_2 <- emp.data[c(3, 5), c(2, 4)]
	# 行、列list获取特定行、列

emp.data$dept <- c("IT", "Operations", "IT", "HR", "Finance")
	# 新列名添加新列

emp.newdata <- data.frame(
	emp_id = c(6: 8),
	emp_name = c("Rasmi","Pranab","Tusar"),
	salary = c(578.0,722.5,632.8), 
	start_date = as.Date(c("2013-05-21","2013-07-30","2014-06-17")),
	dept = c("IT","Operations","Fianance"),
	stringsAsFactors = FALSE
)
emp.finaldata <- rbind(emp.data, emp.newdata)
	# `rbind`将新DF同原DFconcat，达到添加新行

拼、接

rbind

结合两个DF对象行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
city <- c("Tampa", "Seattle", "Hartford", "Denver")
state <- c("FL", "WA", "CT", "CO")
zipcode <- c(33602, 98104, 06161, 80294)

address <- cbind(city, state, zipcode)
	# `cbind`连接多个向量创建DF

new.address <- data.frame(
	city = c("Lowry", "Charlotte"),
	state = c("CO", "FL"),
	zipcode = C("80230", "33949"),
	stringAsFactors = FALSE
)
	# 使用`data.fram`创建DF

all.address <- rbind(
	address,
	new.address
)
	# `rbind`结合两个DF的行
merge

根据两DF列进行merge

1
2
3
4
5
6
7
8
9
10
lirary(MASS)
	# 加载数据集

merged.Pima <- merge(
	x = Pima.te,
	y = Pima.tr,
	by.x = c("bp", "bmi"),
	by.y = c("bp", "bmi")
)
	# 根据DF某（些）列merge
melt、cast
1
2
3
4
5
6
7
8
9
10
11
12
13
library(MASS)
library(reshape2)
melton.ships <- melt(
	ships,
	id = c("type", "year")
)
	# `melt`将剩余列转换为`variable`、`value`标识

recasted.ship <- cast(
	molten.ship,
	type+year~variable,sum
)
	# 和`melt`相反，以某些列为“轴”合并

绑定

attach、detach
1
2
3
4
5
6
7
8
9
10
11
12
13
attach(emp.data)
	# `attach`可以将数据框加入R的搜索路径
	# 之后R遇到变量名之后，将检查搜索路径的数据框
	# 注意，如果之前环境中已经有df对象列同名变量，那么原始
		# 对象优先，不会被覆盖

	emp.data.cols.copy <- data.frame(
		emp_name,
		salary
	)
		# 否则需要之前一样使用`$`
detach(emp.data)
	# 将数据框从搜索路径移除
with
1
2
3
4
5
6
7
8
9
10
with(emp.data, {
	emp.data.cols.copy <<- data.frame(
		emp_name,
		salary
	)
})
	# `{}`中的语句都针对`emp.data`执行，如果只有一条语句，
		# 花括号可以省略
	# `with`语句内`<-`赋值仅在其作用于内生效，需要使用`<<-`
		# 特殊赋值符保存至“全局”变量中

Factor

分类变量、有序变量在R中称为因子，其决定了数据的分析方式、 如何进行视觉呈现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
fctr <- factor(
	vector(c(factors)),
	ordered = FALSE/TRUE,
	levels = c(ordered_unique_factors),
	labels = c(factor_labels)

	# `ordered`：默认不是有序变量
	# `levels`：指定factors的“排序”，确定映射的整数值，
		# 对于分类变量也可以设置
		# 没有在`levels`中显式指定的factor视为缺失
	# `labels`：设置各factor labels，输出则按照labels输出
		# 注意`labels`顺序必须和`levels`一致
		# 对数值型factor尤其有用
)
  • factor以整形向量的形式存储类别值
    • 整数取值范围为1~k，k为定性（分类、有序）变量中 唯一值个数
  • 同时一个由字符串（原始值）组成的内部向量将映射到这些整数
    • 分类变量：字符串映射的整数值由字母序决定
    • 有序变量：按字母序映射可能与逻辑顺序不一致，可以使用 参数levels指定顺序

List

一些对象、成分的有序集合

  • 允许整合若干（可能无关）的对象到单个对象下
  • 很多R函数结果运行结果以列表形式返回，由调用者决定使用 其中何种成分
1
2
3
4
5
6
7
8
9
10
11
12
13

l <- list(
	[name1 =]object1,
	[name2 =]object2,
	...
)
	# 可以给列表中的对象命名
	# 命名成分`l$name1`也可以正常运行


list1 <- list(c(2, 5, 3), 21, 3, sin)
print(list1)
print(class(list1))

运算符

算术运算符

算术操作符作用与向量的每个元素

1
2
3
4
5
6
7
8
9
10
11
12
13
v <- c(2, 5.5, 6)
t <- c(8, 3, 4)
print(v + t)
	# 算术操作符作用与向量的每个元素
print(v - t)
print(v * t)
print(v/t)
print(v %% t)
	# 向量求余
print(v %/% t)
	# 求商
print(v ^ t)
	# 指数运算

关系运算符

比较两个向量的相应元素，返回布尔值向量

1
2
3
4
5
6
7
8
9
v <- c(2, 5.5, 6, 9)
t <- c(8, 2.5, 14, 9)
print (v > t)
	# 比较两个向量的相应元素，返回布尔值向量
print (v < t)
print (v == t)
print (v != t)
print (v <= t)
print (v >= t)

逻辑运算符

只适用于逻辑、数字、复杂类型向量，所有大于1的数字被认为是 逻辑值TRUE

1
2
3
4
5
6
7
8
9
10
v <- c(3, 1, TRUE, 2+3i)
t <- c(4, 1, False, 2+3i)
print(v & t)
	# 比较两个向量相应元素，返回布尔值向量
print(v | t)
print(!v)

print(v && t)
	# 只考虑向量的第一个元素，输出单个bool值元素向量
print(v || t)

其他运算符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
t <- 2: 8
	# 为向量按顺序创建一系列数字

v1 <- 8
v2 <- 12
print (v1 %in% t)
print (v2 %in% t)
	# 标识元素是否属于向量

M = matrix(c(2, 6, 5, 1, 10, 4),
	nrow = 2,
	ncol = 3,
	byrow = TRUE)
t = M %*% t(M)
	# 矩阵相乘

R语句

条件

1
2
3
if
else
switch

循环

1
2
3
4
5
repeat
while
for
break
next

函数

1
2
3
4
5
func_name <- function(
	arg_1,
	arg_2,...){

}

R内置函数

1
2
3
print(seq(32, 44))
print(mean(25: 82))
print(sum(41: 68))

自定义参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
new.function_1 <- fucntion(){
	# 无参数函数
	for(i in 1: 5){
		print(i ^ 2)
	}
}
new.function_1()

new.function_2 <- function(a, b, c){
	# 有参数函数
	result <- a * b + c
	print(result)
}
new.function_2(5, 3, 11)
	# 按参数顺序调用函数
new.function_2(
	a = 11,
	b = 5,
	c = 3)
	# 按参数名称调用

new.function_3 <- function(a=3, b=6){
	# 含有默认参数函数
	result <- a * b
	print(result)
}
new.function_3
	# 无参数（使用默认参数）
new.function_3(9, 5)

函数功能延迟计算

1
2
3
4
5
6
7
new.function <- function(a, b){
	print(a ^ 2)
	print(a)
	print(b)
}
new.function(6)
	# 调用函数能部分执行成功，直到`print(b)`

包

R语言包是R函数、编译代码、样本数据的集合

  • 存储在R环境中名为library的目录下
  • 默认情况下，只有R安装时提供默认包可用，已安装的其他包 必须显式加载
1
2
3
4
5
6
7
8
.libPaths()
	# 获取包含R包的库位置

library()
	# 获取已安装所有软件包列表

search()
	# 获取当前R环境中加载的所有包

安装包

加载包

1
2
3
library("pkg_name",
	lib.loc=/path/to/library)
	# `lib.loc`参数默认应该就是`.libPaths`，一般不用设置
Posted Updated Algorithm44 minutes read (About 6539 words)

算法分析

基础

算法：一系列解决问题的明确指令，即对于符合一定规范的 输入，能够在有限时间内获得要求的输出

  • 算法每步都必须没有歧义
  • 必须确定算法所处理的输入的值域
  • 同一算法可以用几种不同的形式描述
  • 同一问题，可能存在几种不同的算法
  • 同问题的不同算法，可能基于不同的解题思路，速度也会不同

算法正确性证明

  • 对某些算法，正确性证明十分简单，对于另一些算法，可能十分 复杂
  • 证明正确性的一般方法是使用数学归纳法，因为算法的迭代过程 本身就符合其所需的一系列步骤
  • 根据特定输入追踪算法操作有意义，但是并不能证明算法的 正确性，只需要一个算法不能正确处理的输入实例就足够了
  • 对于近似算法，常常试图证明算法所产生的误差，不超出预定义 的误差

算法分析方向

  • 时间效率（time efficiency）：算法运行速度
  • 空间效率（space efficiency）：算法需要多少额外的存储空间
  • 简单性（simplicity）：取决于审视者的眼光
    • 简单的算法更容易理解、实现
    • 相应程序包含更少的bug
  • 一般性（generality）
    • 所解决问题的一般性
    • 所接受输入的一般性
  • 最优性（optimality）：与所解决问题的复杂度有关，与某算法 效率无关
  • 是否每个问题都能够用算法的方法来解决

非确定性

Deterministic Alogrithm

确定算法：利用问题解析性质，产生确定的有限、无限序列使其收敛 于全局最优解

  • 依某确定性策略搜索局部极小，试图跳跃已获得的局部极小而 达到某个全局最优点

  • 能充分利用问题解析性质，从计算效率高

Nondeterministic Algorithm

不确定算法，包括两个阶段，将判定问题的实例l作为其输入

  • 猜测（非确定）阶段：生成任意串S作为l候选解
  • 验证（确定）阶段：把l、S作为输入，，若S是l解输出是， 否则返回否或无法停止

  • 当选仅当对问题每个真实例，不确定算法会在某次执行中 返回是时，称算法能求解此问题

  • 即要求不确定算法对某个解至少能够猜中一次、验证正确性， 同时不应该将错误答案判定为是

  • Nondeterministic Polynominal Algorithm：验证阶段时间 效率是多项式级的不确定算法

分析框架

  • time complexity：算法运行速度
  • space complexity：算法需要的额外空间
    • 算法需要的额外空间已经不是需要重点关注的问题

影响因素

输入规模$n$

  • 几乎所有算法，对规模更大的输入需要运行更长时间，因此使用 输入规模作为参数很有价值

  • 在有些情况下，选择不同的参数表示输入规模有差别

  • 选择输入规模的度量单位还受到算法的操作细节影响

  • 和数字特性相关的算法，倾向于使用$n$的二进制位数 $b=\lfloor {log_{2}^{n}} \rfloor + 1$

其他因素

有些算法的运行时间不仅取决于输入规模，还取决于特定输入的细节

  • worst-case efficiency：最坏情况下的效率
  • best-case efficiency：最优情况下的效率
  • average-case efficiency
    • 平均效率的研究比最差、优效率研究困难很多
    • 可以将输入划分为几种类型，使得对同类实例，算法基本 执行次数相同，推导各类输入的概率分布，得到平均次数
  • amortized efficiency：应用于算法对同样的数据结构所执行 的一系列操作
    • 有些情况下，算法单次执行时间代价高，但是n次运行的 总运行时间明显优于单次执行最差效率 * n

衡量角度

运行时间

  • 使用时间标准的度量算法程序运行时间缺陷

    • 计算机速度
    • 程序实现质量
    • 编译器
    • 计时困难

  • 找到basic operation并计算其运行次数

    • 不依赖于其他无关因素
    • 对总运行时间贡献最大，不需要统计算法每步操作执行次数
    • 如：对排序基本操作为键比较，数学问题则是四则运算， 需要注意除法、乘法、加减法耗时依次减小

  • 时间估计

    • $c_{op}$：特定计算一个基本操作的执行时间
    • $C(n)$：算法执行基本操作的次数
    • $T(n)=c_{op}C(n)$：可以用于估算算法的执行时间
      • 需要小心使用
      • $C(n)$不包含非基本操作的信息，也只是估计的结果
      • $c_{op}$也是不可靠的估计值

Order of Growth

小规模输入运行时间差别不足以将高效算法与低效算法相区别， 对大规模输入忽略乘法常量，仅关注执行次数的order of growth 及其常数倍，即算法的渐进效率

  • 按照算法渐进效率进行分类的方法缺乏使用价值，因为没有指定 乘法常量的值

  • 但是对于实际类型输入，除了少数算法，乘法常量之间不会相差 悬殊，作为规律，即使是中等规模的输入，属于较优渐进 效率类型的算法也会比来自较差类型的算法效果好

  • 对数函数：增长慢，以至于可以认为，对数级操作次数的算法能 瞬间完成任何实际规模输入

  • 指数级：指数函数、阶乘函数
    • 需要指数级操作次数的算法只能用于解决规模非常小的问题

渐进效率

渐进符号

$O(g(n))$

  • 对于足够大的n，$t(n)$的上界由$g(n)$的常数倍确定，则 $t(n) \in O(g(n))$

  • 即存在大于0的常数$c$、非负整数$n_{0}$，使得

  • 增长次数小于等于$g(n) n \rightarrow \infty$ （及常数倍）的函数集合

$\Omega (g(n))$

  • 对于足够大的n，$t(n)$的下界由$g(n)$的常数倍确定，则 $t(n) \in \Omega(g(n))$

  • 即存在大于0的常数$c$、非负整数$n_{0}$，使得

  • 增长次数大于等于$g(n) n \rightarrow \infty$ （及常数倍）的函数集合

$\Theta (g(n))$

  • 对于足够大的n，$t(n)$的上、下界由$g(n)$的常数倍确定，则 $t(n) \in \Theta(g(n))$

  • 即存在大于0的常数$c{1}, c{2}$、非负整数$n_{0}$，使得

  • 增长次数等于$g(n) n \rightarrow \infty$（及常数倍） 的函数集合

极限比较增长次数

利用极限比较增长次数：比直接利用定义判断算法的增长次数方便， 可以使用微积分技术计算极限

基本渐进效率类型

类型 名称 注释
$1$ 常量 很少，效率最高
$log_{n}$ 对数 算法的每次循环都会消去问题规模的常数因子，对数算法不可能关注输入的每个部分
$n$ 线性 能关注输入每个部分的算法至少是线性运行时间
$nlog_{n}$ 线性对数 许多分治算法都属于此类型
$n^{2}$ 平方 包含两重嵌套循环的典型效率
$n^{3}$ 立方 包含三重嵌套循环的典型效率
$2^{n}$ 指数 求n个元素的所有子集
$n!$ 阶乘 n个元素集合的全排列

算法的数学分析

非递归算法

分析通用方案

  1. 决定表示输入规模的参数
  2. 找出算法的基本操作：一般位于算法最内层循环
  3. 检查算法基本操作执行次数是否只依赖于输入规模，如果和其他 特性有关，需要分别研究最差、最优、平均效率
  4. 建立算法基本操作执行次数的求和表达式（或者是递推关系）
  5. 利用求和运算的标准公式、法则建立操作次数的闭合公式，或 至少确定其增长次数

递归算法

用一个方程把squence的generic term和一个或多个其他项相关联， 并提供第一个项或前几项的精确值

  • recurrence：递推式
  • initial condition：序列起始值、递归调用结束条件
  • 求解：找到序列通项的精确公式满足递推式、初始条件，或者 证明序列不存在
  • general solution：满足递推方程所有解序列公式，通常 会包含参数
  • particular solution：满足给定递推方程的特定序列，通常 感兴趣的是满足初始条件的特解

递归求解方法

  • method of forward substituion：从序列初始项开始，使用 递推方程生成给面若干项，从中找出能用闭合公式表示的模式

    • 带入递推方程、初始条件验证
    • 数学归纳法证明

  • method of backward subsitution：从序列末尾开始，把序列 通项$x(n)$表示为$x(n-i)$的函数，使得i是初始条件之一， 再求和公式得到递推式的解

  • second-order linear recurrence with constant coefficients ：求解characteristic equation得到特征根得到通解

常见递推类型

decrease-by-one

减一法：利用规模为n、n-1的给定实例之间的关系求解问题

  • 减常数法特例
decrease-by-a-constant-factor

减常因子法：把规模为n的实例化简为规模为n/b的实例求解问题

divide-and-conquer

分治法：将给定实例划分为若干较小实例，对每个实例递归求解，如有必要， 再将较小实例的接合并为给定实例的一个解

平滑法则、主定理

  • eventually nondecreaing：$f(n)$在自然数上非负，若 $\exists n{0}, \forall n{2} > n{1} \geqslant n{0}, f(n{2}) > f(n{1})$， 则为最终非递减

  • smooth：$f(n)$在自然数上非负、最终非递减，若 $f(2n) \in \Theta(f(n))$，则平滑

    • 若$f(n)$平滑，则对任何整数b有$f(bn) \in \Theta(f(n))$
平滑法则

$T(n)$最终非递减，$f(n)$平滑，若$n=b^{k}(b>2)$时有 $T(n) \in \Theta(f(n))$，则$T(n) \in \Theta(f(n))$

主定理
  • 方便对分治法、减常因子法效率进行分析

$T(n)$最终非递减，满足递推式

若$f(n) \in \Theta(n^{d}), d \geqslant 0$，则

分析通用方案

  1. 决定衡量输入规模的参数
  2. 找出算法基本操作
  3. 检查算法基本操作执行次数是否只依赖于输入规模，如果和其他 特性有关，需要分别研究最差、最优、平均效率
  4. 建立算法基本操作执行次数的递推关系、相应初始条件
  5. 求解递推式，或至少确定其增长次数

算法时间效率极限

确定已知、未知算法效率极限

算法下界

算法下界是问题可能具有的最佳效率

  • 可以用于评价某问题具体算法效率

    • 不同问题算法直接比较无意义

  • 寻找问题的更优算法时，可以根据算法下界确定期望获得的改进

    • 若算法下界是紧密的，则改进至多不过是常数因子
    • 若算法下界和算法仍有差距，则可能存在更快算法，或者是 证明更好的下界

Trivial Lower Bound

平凡下界：任何算法只要要“读取”所有要处理的项、“写”全部 输出，对其计数即可得到平凡下界

  • 往往过小，用处不大

  • 确定问题中所有算法都必须要处理的输入也是个障碍

  • 例

    • 生成n个不同项所有排列的算法$\in \Omega(n!)$，且下界 是紧密的，因为好的排列算法在每个排列上时间为常数

    • 计算n次多项式值算法至少必须要处理所有系数，否则改变 任意系数多项式值改变，任何算法$\in \Omega(n)$

    • 计算两个n阶方阵乘积算法$\in Omega(n^2)$，因为任何 算法必须处理矩阵中$2n^2$个元素

Information-Theoretic Lower Bound

信息论下界：试图通过算法必须处理的信息量（比特数）建立 效率下界

  • 例

    • 猜整数中，整数的不确定信息量就是 $\lceil \log_2 n \rceil$（数字二进制位数）， n为整数上界

Adversary Lower Bound

敌手下界：敌手基于恶意、一致的逻辑，迫使算法尽可能多执行， 从而确定的为了保证算法正确性的下界

  • 恶意使得它不断把算法推向最消耗时间的路径
  • 一致要求它必须和已经做出的选择保持一致（按照一定规则）

  • 例

    • 猜整数中，敌手把1~n个数字作为可选对象，每次做出判断 后，敌手保留数字较多集合，使得最消耗时间、不违背之前 选择

    • 两个有序列表${a_i}, {b_j}$归并排序中，敌手使用规则： 当前仅当i < j时，对$a_i < b_j$返回真（设置列表值大小 可以达到），则任何算法必须比较2n-1次，否则交换未比较 元素归并错误

问题化简

问题Q下界已知，考虑将问题Q转换为下界未知问题P，得到P下界

  • 应该表明任意Q问题实例可以转换为P问题
  • 即问题Q应该是问题P的子集，正确的算法至少应该能解决Q问题

  • 许多问题复杂性不清楚，而对问题复杂度的直观判断和问题表现 形式相关，并不可靠

  • 常在问题化简中使用的已知下界问题

    |问题|下界|紧密性| |——-|——-|——-| |排序|$\Omega(nlogn)$|是| |有序数组查找|$\Omega(logn)$|是| |元素惟一性|$\Omega(nlogn)$|是| |n位整数乘法|$\Omega(n)$|未知| |n阶方程点乘|$\Omega(n^2)$|未知|

  • 例

    • 欧几里得最小生成树：使用元素唯一性问题作为下界已知 问题

      • 将n个实数映射为x轴上的n个点
      • 设T为此点集最小生成树，T必然包含一条最短边??#todo
      • 检查T是否包含长度为0的边即为元素惟一性

    • 任意矩阵A、B乘法：使用方阵乘法作为下界已知问题

      • 将A、B化成对称方阵进行计算

      • 乘积AB可以方便提取，而翻倍的矩阵乘法不会影响复杂性

决策树（二叉）

可以使用（二叉）决策树研究基于比较的算法性能

  • 每个非叶子节点代表一次键值比较

  • 叶子节点个数大于等于输出，不同叶子节点可以产生相同输出

  • 对于特定规模为n的输入，算法操作沿着决策树一条从根到叶子 节点完成，所以最坏情况下比较次数等于算法决策树高度

  • 如果树具有由输出数量确定叶子，则树必须由足够高度容纳叶子 ，即对于任何具有$l$个叶子，树高度 $h \leqslant \lceil log_2 l \rceil$，这也就是 信息论下界

线性表排序

任意n个元素列表排序输出数量等于$n!$，所以任何基于比较的排序 算法的二叉树高度，即最坏情况下比较次数

  • 归并排序、堆排序在最坏情况下大约必须要做$nlog_2n$次比较 ，所以其渐进效率最优

  • 也说明渐进下界$\lceil log_2n! \rceil$是紧密的 ，不能继续改进

    • 但这个只是基于二叉决策树的渐进下界，对于具体值估计 可能不准

    • 如$\lceil log_2 12! \rceil = 29$，而事实证明 12个元素排序30次比较是必要、充分的

  • 也可以使用决策树分析基于比较的排序算法的平均性能，即 决策树叶子节点平均深度

    • 基于排序的所有输出都不特殊的标准假设，可以证明平均 比较次数下界$C_{avg}(n) \geqslant log_2n!$

    • 这个平均是建立在所有输出都不特殊假设上，所以这个其实 应该是不同算法平均比较次数下界的上界

    • 对于单独排序算法，平均效率会明显好于最差效率

有序线性表查找

有序线性表查找最主要算法是折半查找，其在最坏情况下下效率 $C{worst}^{bs} = \lfloor log_2n \rfloor + 1 = \lceil log(n+1) \rceil$

  • 折半查找使用的三路比较（小于、等于、大于），可以使用 三叉查找树表示

    • 三叉查找树会有2n+1个节点：n个查找成功节点、n+1个查找 失败节点

    • 所以在最坏情况下，比较次数下界 $C_{worst}(n) \geqslant \lceil log_3{2n+1} \rceil$ 小于折半查找最坏情况下比较次数（渐进）

  • 然而，事实上可以删除三叉查找树中间子树（等于分支），得到 一棵二叉树

    • 非叶子节点同样表示三路比较，只是同时作为查找成功终点

    • 可以得到一个新的下界 $C_{worst}(n) \geqslant \lceil log_2{n+1} \rceil$

  • 更复杂的分析表明，标准查找假设下，折半查找平均情况比较 次数是最少的

    • 查找成功时$log_2n - 1$
    • 查找失败时$log_2(n+1)$

P、NP、完全NP问题

复杂性理论

  • 如果算法的最差时间效率$\in O(p(n))$，$p(n)$为问题输入 规模n的多项式函数，则称算法能在多项式时间内对问题求解

  • Tractable：易解的，可以在多项式时间内求解的问题

  • Intractable：难解的，不能在多项式内求解的问题

使用多项式函数理由

  • 无法保证在合理时间内对难解问题所有实例求解，除非问题实例 非常小

  • 对实用类型的算法而言，其多项式次数很少大于3，虽然多项式 次数相差很大时运行时间也会有巨大差别

  • 多项式函数具有方便的特性

    • 多项式加和、组合也为多项式

  • 多项式类型可以发展出Computational Complexity利用

    • 该理论试图对问题内在复杂性进行分类
    • 只要使用一种主要计算模型描述问题，并用合理编码方案 描述输入，问题难解性都是相同的

Decision Problem

判定问题：寻求一种可行的、机械的算法，能够对某类问题在有穷 步骤内确定是否具有某性质

  • Undecidable问题：不可判定问题，不能使用任何算法求解的 判定问题

    • 停机问题：给定程序、输入，判断程序对于输入停止还是 无限运行下去

  • Decidable问题：可判定问题，能用算法求解的问题

    • 可判定、难解问题存在，但非常少

    • 很多判定问题（或者可以转化为等价判定问题），既没有 找到多项式类型算法，也没有证明这样算法不存在，即无法 判断是否难解

P、NP问题

P问题

Polynomial类型问题

  • 非正式定义：易解的问题，即能够在多项式时间内求解的 问题（计算机范畴）

  • 正式定义：能够用确定性算法在多项式时间内求解的 判定问题

  • 多项式时间内求解：排除难解问题

  • 判定问题：很多重要问题可以化简为更容易研究的判断问题 ，虽然原始表达形式不是判定问题

NP问题

Nondeterministic Polynomial类型问题：可以用不确定多项式 算法求解的判定问题

  • NP问题虽然计算上对问题求解困难，但是在计算上判定待定结 是否解决问题是简单的：可以在多项式时间内完成

  • 大多数判断问题都是属于NP类型的

    • $P \subseteq NP$：如果问题属于P，在不确定算法验证 阶段忽略猜测

    • 还包括以下没有找到多项式算法、也没有证明算法不存在 的组合优化问题的判定版本

      • 哈密顿回路问题
      • 旅行商问题
      • 背包问题
      • 划分问题
      • 装箱问题
      • 图着色问题
      • 整数线性规划问题

  • $P \overset ? = NP$：P和NP问题是否一致，计算机科学理论 中最重要的未解之谜

    • P = NP意味着虽然没有找到，但能够在多项式时间内求解 许多组合优化问题确实存在

NPC问题

NP Complete问题

  • 属于NP问题种，和该类型其他问题难度一致
  • 证明问题属于NP问题比较简单
  • NP中其他任何问题（已知或未知）可以在多项式时间内化简为 NPC问题

  • 直接证明任何NP问题都可以在多项式时间内化简为当前问题 比较困难

  • 常常利用多项式规约特性，证明某个确定NPC问题可以 多项式规约为当前问题

  • 判定问题相互转换例

    • 哈密顿回路问题中图G映射加权图$G^{‘}$，G中存在边在 权重为1，不存在边权重为2，则哈密顿回路问题转换为$G^{‘}$ 是否存在长度不超过$|V|$的哈密顿回路，即旅行商问题的等价

  • NPC问题案例

    • CNF-Satisfied Problem：合取范式可满足性问题，首个 被发现NPC问题

    • 前面提到的著名NP问题都是NPC问题

      • 包括哈密顿回路问题？？？

  • 仅仅得到一个NPC问题的多项式确定算法，所有NP问题可以 在多项式时间内求解

    • 则$P = NP$

    • 即对于所有类型判定问题而言，检验待定解、在多项式时间 内求解在复杂性商没有本质区别

  • 而NPC问题可以被其他NP问题转换而来意味着，NPC问题目前不 存在对所有实例通用的多项式时间算法

NP-Hard问题

NP-Hard问题：所有NP问题都可以通过多项式规约到其

  • 不满足NPC问题第一个条件，可以不是NP问题

  • 其范围包含NPC问题，前述组合优化问题最优版本也是NP-Hard

  • 可以理解为：至少和NPC问题一样困难的问题

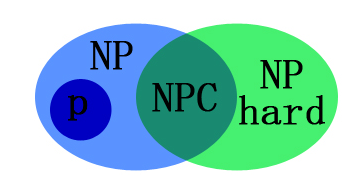
p_np_npc_nphard

Reference

Polynomially Reducible

判定问题$D_1$可以多项式规约为判定问题$D_2$，条件是存在 函数t可以把$D_1$的实例转换为$D_2$的实例，满足

  • t把$D_1$所有真实例映射为$D_2$真实例，把$D_1$所有假实例 映射为$D_2$假实例

  • t可以用多项式算法计算

CNF-Satisfied Problem

合取范式满足性问题：能否设置合取范式类型的布尔表达式中布尔 变量值，使得整个表达式值为真

  • 每个布尔表达式都可以表达为合取范式
Posted Updated Python / Keras14 minutes read (About 2173 words)

卷积层

Conv1D

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
keras.layers.convolutional.Conv1D(
	filters(int),
	kernel_size(int),
	strides=1,
	padding='valid',
	dilation_rate=1,
	activation=None,
	use_bias=True,
	kernel_initializer='glorot_uniform',
	bias_initializer='zeros',
	kernel_regularizer=None,
	bias_regularizer=None,
	activity_regularizer=None,
	kernel_constraint=None,
	bias_constraint=None
)

一维卷积层（即时域卷积）

  • 说明

    • 用以在一维输入信号上进行邻域滤波
    • 作为首层时，需要提供关键字参数input_shape
    • 该层生成将输入信号与卷积核按照单一的空域（或时域） 方向进行卷积
    • 可以将Convolution1D看作Convolution2D的快捷版

  • 参数

    • filters：卷积核的数目（即输出的维度）

    • kernel_size：整数或由单个整数构成的list/tuple， 卷积核的空域或时域窗长度

    • strides：整数或由单个整数构成的list/tuple，为卷积 步长

      • 任何不为1的strides均与任何不为1的dilation_rate 均不兼容

    • padding：补0策略

    • activation：激活函数

    • dilation_rate：整数或由单个整数构成的list/tuple， 指定dilated convolution中的膨胀比例

      • 任何不为1的dilation_rate均与任何不为1的strides 均不兼容

    • use_bias：布尔值，是否使用偏置项

    • kernel_initializer：权值初始化方法

      • 预定义初始化方法名的字符串
      • 用于初始化权重的初始化器（参考initializers）

    • bias_initializer：偏置初始化方法

      • 为预定义初始化方法名的字符串
      • 用于初始化偏置的初始化器

    • kernel_regularizer：施加在权重上的正则项，为 Regularizer对象

    • bias_regularizer：施加在偏置向量上的正则项

    • activity_regularizer：施加在输出上的正则项

    • kernel_constraints：施加在权重上的约束项

    • bias_constraints：施加在偏置上的约束项

  • 输入：形如(batch, steps, input_dim)的3D张量

  • 输出：形如(batch, new_steps, filters)的3D张量

    • 因为有向量填充的原因，steps的值会改变

Conv2D

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
keras.layers.convolutional.Conv2D(
	filters,
	kernel_size,
	strides=(1, 1),
	padding='valid',
	data_format=None,
	dilation_rate=(1, 1),
	activation=None,
	use_bias=True,
	kernel_initializer='glorot_uniform',
	bias_initializer='zeros',
	kernel_regularizer=None,
	bias_regularizer=None,
	activity_regularizer=None,
	kernel_constraint=None,
	bias_constraint=None
)

二维卷积层，即对图像的空域卷积

  • 说明

    • 该层对二维输入进行滑动窗卷积
    • 当使用该层作为第一层时，应提供

  • 参数

    • filters：卷积核的数目（即输出的维度）

    • kernel_size：单个整数或由两个整数构成的list/tuple， 卷积核的宽度和长度

      • 如为单个整数，则表示在各个空间维度的相同长度

    • strides：单个整数或由两个整数构成的list/tuple， 卷积的步长

      • 如为单个整数，则表示在各个空间维度的相同步长
      • 任何不为1的strides均与任何不为1的dilation_rate 均不兼容

    • padding：补0策略

    • activation：激活函数

    • dilation_rate：单个或两个整数构成的list/tuple， 指定dilated convolution中的膨胀比例

      • 任何不为1的dilation_rate均与任何不为1的strides 均不兼容

  • 输入：(batch, channels, rows, cols) （”channels_first”）4D张量

  • 输出：(batch, filters, new_rows, new_cols) （”channels_first”）4D张量

    • 输出的行列数可能会因为填充方法而改变

SeparableConv2D

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
keras.layers.convolutional.SeparableConv2D(
	filters,
	kernel_size,
	strides=(1, 1),
	padding='valid',
	data_format=None,
	depth_multiplier=1,
	activation=None,
	use_bias=True,
	depthwise_initializer='glorot_uniform',
	pointwise_initializer='glorot_uniform',
	bias_initializer='zeros',
	depthwise_regularizer=None,
	pointwise_regularizer=None,
	bias_regularizer=None,
	activity_regularizer=None,
	depthwise_constraint=None,
	pointwise_constraint=None,
	bias_constraint=None
)

该层是在深度方向上的可分离卷积。

  • 说明

    • 首先按深度方向进行卷积（对每个输入通道分别卷积）
    • 然后逐点卷积，将上步卷积结果混合到输出通道中
    • 直观来说，可分离卷积可以看做讲一个卷积核分解为两个小 卷积核，或看作Inception模块的一种极端情况

  • 参数

    • depth_multiplier：按深度卷积的步骤中，每个输入通道 使用（产生）多少个输出通道

    • depthwise_regularizer：按深度卷积的权重上的正则项

    • pointwise_regularizer：按点卷积的权重上的正则项

    • depthwise_constraint：按深度卷积权重上的约束项

    • pointwise_constraint：在按点卷积权重的约束项

  • 输入：(batch, channels, rows, cols)4DT （”channels_first”)

  • 输出：(batch, filters, new_rows, new_cols)4DTK （”channels_first”）

    • 输出的行列数可能会因为填充方法而改变

Conv2DTranspose

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
keras.layers.convolutional.Conv2DTranspose(
	filters,
	kernel_size,
	strides=(1, 1),
	padding="valid",
	output_padding=None/int/tuple,
	data_format=None,
	activation=None,
	use_bias=True,
	kernel_initializer="glorot_uniform",
	bias_initializer="zeros",
	kernel_regularizer=None,
	bias_regularizer=None,
	activity_regularizer=None,
	kernel_constraint=None,
	bias_constraint=None
)

该层是反卷积操作（转置卷积）

Conv3D

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
keras.layers.convolutional.Conv3D(
	filters,
	kernel_size,
	strides=(1, 1, 1),
	padding='valid',
	data_format=None,
	dilation_rate=(1, 1, 1),
	activation=None,
	use_bias=True,
	kernel_initializer='glorot_uniform',
	bias_initializer='zeros',
	kernel_regularizer=None,
	bias_regularizer=None,
	activity_regularizer=None,
	kernel_constraint=None,
	bias_constraint=None
)

三维卷积对三维的输入（视频）进行滑动窗卷积

  • 输入：(batch, channels, conv_dim1, conv_dim2, conv_dim3) 5D张量（”channnels_first”）

Cropping1D

1
2
3
keras.layers.convolutional.Cropping1D(
	cropping=(1, 1)/tuple/int
)

在时间轴上对1D输入（即时间序列）进行裁剪

  • 参数

    • cropping：指定在序列的首尾要裁剪掉多少个元素
      • 单值表示首尾裁剪相同

  • 输入：(batch, axis_to_crop, features)的3DT

  • 输出：(batch, cropped_axis, features)的3DT

Cropping2D

1
2
3
4
keras.layers.convolutional.Cropping2D(
	cropping=((0, 0), (0, 0)),
	data_format=None
)

对2D输入（图像）进行裁剪

  • 说明

    • 将在空域维度，即宽和高的方向上裁剪

  • 参数

    • cropping：长为2的整数tuple，分别为宽和高方向上头部 与尾部需要裁剪掉的元素数
      • 单值表示宽高、首尾相同
      • 单元组类似

  • 输入：(batch, rows, cols, channels)4DT（”channels_last”）

  • 输出：(batch, cropped_rows, cropped_cols, channels)

1
2
3
4
5
6
7
8
	# Crop the input 2D images or feature maps
model = Sequential()
model.add(Cropping2D(cropping=((2, 2), (4, 4)),
                     input_shape=(28, 28, 3)))
	# now model.output_shape == (None, 24, 20, 3)
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Cropping2D(cropping=((2, 2), (2, 2))))
	# now model.output_shape == (None, 20, 16, 64)

Cropping3D

1
2
3
4
keras.layers.convolutional.Cropping3D(
	cropping=((1, 1), (1, 1), (1, 1)),
	data_format=None
)

对3D输入（空间、时空）进行裁剪

  • 参数

    • cropping：长为3的整数tuple，分别为三个方向上头部 与尾部需要裁剪掉的元素数

  • 输入：(batch, depth, first_axis_to_crop, second_axis_to_crop, third_axis_to_crop) （”channels_first”）

  • 输出：(batch, depth, first_cropped_axis, second_cropped_axis, third_cropped_axis)

UpSampling1D

1
2
3
keras.layers.convolutional.UpSampling1D(
	size=2/integer
)

在时间轴上，将每个时间步重复size次

  • 参数

    • size：轴上采样因子

  • 输入：(batch, steps, features)的3D张量

  • 输出：(batch, upsampled_steps, feature)的3D张量

UpSampling2D

1
2
3
4
keras.layers.convolutional.UpSampling2D(
	size=(2, 2)/tuple/int,
	data_format=None
)

将数据的行和列分别重复size[0]和size[1]次

  • 参数

    • size：分别为行和列上采样因子

  • 输入：(batch, channels, rows, cols)的4D张量 （”channels_first”）

  • 输出：(batch, channels, upsampled_rows, upsampled_cols)

UpSampling3D

1
2
3
4
keras.layers.convolutional.UpSampling3D(
	size=(2, 2, 2)/tuple/int,
	data_format=None
)

将数据的三个维度上分别重复size次

  • 说明

    • 本层目前只能在使用Theano为后端时可用

  • 参数

    • size：代表在三个维度上的上采样因子

  • 输入：(batch, dim1, dim2, dim3, channels)5DT （”channels_last”）

  • 输出：(batch, upsampled_dim1, upsampled_dim2, upsampled_dim3, channels)

ZeroPadding1D

1
2
3
keras.layers.convolutional.ZeroPadding1D(
	padding=1/int
)

对1D输入的首尾端（如时域序列）填充0

  • 说明

    • 以控制卷积以后向量的长度

  • 参数

    • padding：整数，在axis 1起始和结束处填充0数目

  • 输入：(batch, axis_to_pad, features)3DT

  • 输出：(batch, paded_axis, features)3DT

ZeroPadding2D

1
2
3
4
keras.layers.convolutional.ZeroPadding2D(
	padding=(1, 1)/tuple/int,
	data_format=None
)

对2D输入（如图片）的边界填充0

  • 说明

    • 以控制卷积以后特征图的大小

  • 参数

    • padding：在要填充的轴的起始和结束处填充0的数目

ZeroPadding3D

1
2
3
4
keras.layers.convolutional.ZeroPadding3D(
	padding=(1, 1, 1),
	data_format=None
)

将数据的三个维度上填充0

  • 说明
    • 本层目前只能在使用Theano为后端时可用

结束处填充0的数目

ZeroPadding3D

1
2
3
4
keras.layers.convolutional.ZeroPadding3D(
	padding=(1, 1, 1),
	data_format=None
)

将数据的三个维度上填充0

  • 说明
    • 本层目前只能在使用Theano为后端时可用

?时可用

Posted Updated Python / Keras4 minutes read (About 578 words)

Layers 总述

Layer方法

所有的Keras层对象都有如下方法：

  • layer.get_weights()：返回层的权重NDA

  • layer.set_weights(weights)：从NDA中将权重加载到该层中 ，要求NDA的形状与layer.get_weights()的形状相同

  • layer.get_config()：返回当前层配置信息的字典，层也可以 借由配置信息重构

  • layer.from_config(config)：根据config配置信息重构层

    1
    2
    3
    layer = Dense(32)
    config = layer.get_config()
    reconstructed_layer = Dense.from_config(config)
    1
    2
    3
    4
    5
    from keras import layers

    config = layer.get_config()
    layer = layers.deserialize({'class_name': layer.__class__.__name__,
    							'config': config})

非共享层

如果层仅有一个计算节点（即该层不是共享层），则可以通过下列 方法获得

  • 输入张量：layer.input
  • 输出张量：layer.output
  • 输入数据的形状：layer.input_shape
  • 输出数据的形状：layer.output_shape

共享层

如果该层有多个计算节点（参考层计算节点和共享层）

  • 输入张量：layer.get_input_at(node_index)
  • 输出张量：layer.get_output_at(node_index)
  • 输入数据形状：layer.get_input_shape_at(node_index)
  • 输出数据形状：layer.get_output_shape_at(node_index)

参数

shape类型

  • batch_size

    • batch_size在实际数据输入中为首维（0维）
    • shape类型参数传递的tuple中一般不包括batch_size维度
    • 输出时使用None表示(batch_size,...)

  • time_step

    • 对时序数据，time_step在实际数据输入中第二维（1维）
input_shape

  • 是Layer的初始化参数，所有Layer子类都具有

  • 如果Layer是首层，需要传递该参数指明输入数据形状，否则 无需传递该参数

    • 有些子类有类似于input_dim等参数具有input_shape 部分功能

  • None：表示该维度变长

输入、输出

  • channels/depth/features：时间、空间单位上独立的数据， 卷积应该在每个channal分别“独立”进行

    • 对1维时序（时间），channels就是每时刻的features
    • 对2维图片（空间），channels就是色彩通道
    • 对3维视频（时空），channels就是每帧色彩通道
    • 中间数据，channnels就是每个filters的输出

  • 1D：(batch, dim, channels)（channels_last）

  • 2D：(batch, dim_1, dim_2, channels) （channels_last）

  • 3D：(batch, dim_1, dim_2, dim_3, channels) （channels_last）

Posted Updated Python / Keras3 minutes read (About 472 words)

高级激活层

LeakyReLU

1
keras.layers.LeakyReLU(alpha=0.3)

带泄漏的修正线性单元。

  • 返回值：当神经元未激活时，它仍可以赋予其一个很小的梯度

    • x < 0：alpha * x
    • x >= 0：x

  • 输入尺寸

    • 可以是任意的。如果将该层作为模型的第一层，需要指定 input_shape参数（整数元组，不包含样本数量的维度）

  • 输出尺寸：与输入相同

  • 参数

    • alpha：float >= 0，负斜率系数。

  • 参考文献

PReLU

1
2
3
4
5
6
keras.layers.PReLU(
	alpha_initializer='zeros',
	alpha_regularizer=None,
	alpha_constraint=None,
	shared_axes=None
)

参数化的修正线性单元。

  • 返回值

    • x < 0：alpha * x
    • x >= 0：x

  • 参数

    • alpha_initializer: 权重的初始化函数。
    • alpha_regularizer: 权重的正则化方法。
    • alpha_constraint: 权重的约束。
    • shared_axes: 激活函数共享可学习参数的轴。 如果输入特征图来自输出形状为 (batch, height, width, channels) 的2D卷积层，而且你希望跨空间共享参数，以便每个滤波 器只有一组参数，可设置shared_axes=[1, 2]

  • 参考文献

ELU

1
keras.layers.ELU(alpha=1.0)

指数线性单元

ThresholdedReLU

1
keras.layers.ThresholdedReLU(theta=1.0)

带阈值的修正线性单元。

Softmax

1
keras.layers.Softmax(axis=-1)

Softmax激活函数

  • 参数
    • axis: 整数，应用 softmax 标准化的轴。

ReLU

1
keras.layers.ReLU(max_value=None)

ReLU激活函数

  • 参数
    • max_value：浮点数，最大的输出值。
Posted Updated Python / Keras11 minutes read (About 1690 words)

常用层

常用层对应于core模块，core内部定义了一系列常用的网络层，包括 全连接、激活层等

Dense层

1
2
3
4
5
6
7
8
9
10
11
12
keras.layers.core.Dense(
	units,
	activation=None,
	use_bias=True,
	kernel_initializer='glorot_uniform',
	bias_initializer='zeros',
	kernel_regularizer=None,
	bias_regularizer=None,
	activity_regularizer=None,
	kernel_constraint=None,
	bias_constraint=None
)

Dense就是常用的全连接层

  • 用途：实现运算$output = activation(dot(input, kernel)+bias)$

    • activation：是逐元素计算的激活函数
    • kernel：是本层的权值矩阵
    • bias：为偏置向量，只有当use_bias=True才会添加

  • 参数

    • units：大于0的整数，代表该层的输出维度。

    • activation：激活函数

      • 为预定义的激活函数名（参考激活函数）
      • 逐元素（element-wise）的Theano函数
      • 不指定该参数，将不会使用任何激活函数 （即使用线性激活函数：a(x)=x）

    • use_bias: 布尔值，是否使用偏置项

    • kernel_initializer：权值初始化方法

      • 预定义初始化方法名的字符串
      • 用于初始化权重的初始化器（参考initializers）

    • bias_initializer：偏置向量初始化方法

      • 为预定义初始化方法名的字符串
      • 用于初始化偏置向量的初始化器（参考initializers）

    • kernel_regularizer：施加在权重上的正则项，为 Regularizer对象

    • bias_regularizer：施加在偏置向量上的正则项，为 Regularizer对象

    • activity_regularizer：施加在输出上的正则项，为 Regularizer对象

    • kernel_constraints：施加在权重上的约束项，为
      Constraints对象

    • bias_constraints：施加在偏置上的约束项，为 Constraints对象

  • 输入

    • 形如(batch_size, ..., input_dim)的NDT，最常见情况 为(batch_size, input_dim)的2DT
    • 数据的维度大于2，则会先被压为与kernel相匹配的大小

  • 输出

    • 形如(batch_size, ..., units)的NDT，最常见的情况为 $(batch_size, units)$的2DT

Activation层

1
2
3
4
keras.layers.core.Activation(
	activation,
	input_shape
)

激活层对一个层的输出施加激活函数

  • 参数

    • activation：将要使用的激活函数
      • 预定义激活函数名
      • Tensorflow/Theano的函数（参考激活函数）

  • 输入：任意，使用激活层作为第一层时，要指定input_shape

  • 输出：与输入shape相同

Dropout层

1
2
3
4
5
keras.layers.core.Dropout(
	rate,
	noise_shape=None,
	seed=None
)

为输入数据施加Dropout

  • 参数

    • rate：0~1的浮点数，控制需要断开的神经元的比例

    • noise_shape：整数张量，为将要应用在输入上的二值 Dropout mask的shape

    • seed：整数，使用的随机数种子

  • 输入

    • 例：(batch_size, timesteps, features)，希望在各个 时间步上Dropout mask都相同，则可传入 noise_shape=(batch_size, 1, features)

Flatten层

1
keras.layers.core.Flatten()

Flatten层用来将输入“压平”，把多维的输入一维化

  • 常用在从卷积层到全连接层的过渡
  • Flatten不影响batch的大小。
1
2
3
4
5
6
7
8
model = Sequential()
model.add(Convolution2D(64, 3, 3,
            border_mode='same',
            input_shape=(3, 32, 32)))
	# now: model.output_shape == (None, 64, 32, 32)

model.add(Flatten())
	# now: model.output_shape == (None, 65536)

Reshape层

1
2
3
4
keras.layers.core.Reshape(
	target_shape,
	input_shape
)

Reshape层用来将输入shape转换为特定的shape

  • 参数

    • target_shape：目标shape，为整数的tuple，不包含样本 数目的维度（batch大小）
      • 包含-1表示推断该维度大小

  • 输入：输入的shape必须固定（和target_shape积相同）

  • 输出：(batch_size, *target_shape)

  • 例

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    model = Sequential()
    model.add(Reshape((3, 4), input_shape=(12,)))
    	# now: model.output_shape == (None, 3, 4)
    	# note: `None` is the batch dimension

    model.add(Reshape((6, 2)))
    	# now: model.output_shape == (None, 6, 2)

    	# also supports shape inference using `-1` as dimension
    model.add(Reshape((-1, 2, 2)))
    	# now: model.output_shape == (None, 3, 2, 2)

Permute层

1
2
3
keras.layers.core.Permute(
	dims(tuple)
)

Permute层将输入的维度按照给定模式进行重排

  • 说明

    • 当需要将RNN和CNN网络连接时，可能会用到该层。

  • 参数

    • dims：指定重排的模式，不包含样本数的维度（即下标 从1开始）

  • 输出shape

    • 与输入相同，但是其维度按照指定的模式重新排列

  • 例

    1
    2
    3
    model = Sequential()
    model.add(Permute((2, 1), input_shape=(10, 64)))
    	# now: model.output_shape == (None, 64, 10)

RepeatVector层

1
2
3
keras.layers.core.RepeatVector(
	n(int)
)

RepeatVector层将输入重复n次

  • 参数

    • n：整数，重复的次数

  • 输入：形如(batch_size, features)的张量

  • 输出：形如(bathc_size, n, features)的张量

  • 例

    1
    2
    3
    4
    5
    6
    model = Sequential()
    model.add(Dense(32, input_dim=32))
    	# now: model.output_shape == (None, 32)

    model.add(RepeatVector(3))
    	# now: model.output_shape == (None, 3, 32)

Lambda层

1
2
3
4
5
6
keras.layers.core.Lambda(
	function,
	output_shape=None,
	mask=None,
	arguments=None
)

对上一层的输出施以任何Theano/TensorFlow表达式

  • 参数

    • function：要实现的函数，该函数仅接受一个变量，即 上一层的输出

    • output_shape：函数应该返回的值的shape，可以是一个 tuple，也可以是一个根据输入shape计算输出shape的函数

    • mask: 掩膜

    • arguments：可选，字典，用来记录向函数中传递的其他 关键字参数

  • 输出：output_shape参数指定的输出shape，使用TF时可自动 推断

  • 例

    1
    2
    model.add(Lambda(lambda x: x ** 2))
    	# add a x -> x^2 layer
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    # add a layer that returns the concatenation
    # of the positive part of the input and
    # the opposite of the negative part

    def antirectifier(x):
    	x -= K.mean(x, axis=1, keepdims=True)
    	x = K.l2_normalize(x, axis=1)
    	pos = K.relu(x)
    	neg = K.relu(-x)
    	return K.concatenate([pos, neg], axis=1)

    def antirectifier_output_shape(input_shape):
    	shape = list(input_shape)
    	assert len(shape) == 2  # only valid for 2D tensors
    	shape[-1] *= 2
    	return tuple(shape)

    model.add(Lambda(antirectifier,
    		 output_shape=antirectifier_output_shape))

ActivityRegularizer层

1
2
3
4
keras.layers.core.ActivityRegularization(
	l1=0.0,
	l2=0.0
)

经过本层的数据不会有任何变化，但会基于其激活值更新损失函数值

  • 参数
    • l1：1范数正则因子（正浮点数）
    • l2：2范数正则因子（正浮点数）

Masking层

1
keras.layers.core.Masking(mask_value=0.0)

使用给定的值对输入的序列信号进行“屏蔽”

  • 说明

    • 用以定位需要跳过的时间步
    • 对于输入张量的时间步，如果输入张量在该时间步上都等于 mask_value，则该时间步将在模型接下来的所有层 （只要支持masking）被跳过（屏蔽）。
    • 如果模型接下来的一些层不支持masking，却接受到masking 过的数据，则抛出异常

  • 输入：形如(samples,timesteps,features)的张量

  • 例：缺少时间步为3和5的信号，希望将其掩盖
    • 方法：赋值x[:,3,:] = 0., x[:,5,:] = 0.
    • 在LSTM层之前插入mask_value=0.的Masking层
      1
      2
      3
      model = Sequential()
      model.add(Masking(mask_value=0., input_shape=(timesteps, features)))
      model.add(LSTM(32))

.`的Masking层 

1
2
3
model = Sequential()
model.add(Masking(mask_value=0., input_shape=(timesteps, features)))
model.add(LSTM(32))

```

Posted Updated Python / Keras2 minutes read (About 229 words)

LocallyConnceted 局部连接层

LocallyConnnected和Conv差不多，只是Conv每层共享卷积核， 这里不同位置卷积核独立

LocallyConnected1D层

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
keras.layers.local.LocallyConnected1D(
	filters,
	kernel_size,
	strides=1,
	padding="valid",
	data_format=None,
	activation=None,
	use_bias=True,
	kernel_initializer="glorot_uniform",
	bias_initializer="zeros",
	kernel_regularizer=None,
	bias_regularizer=None,
	activity_regularizer=None,
	kernel_constraint=None,
	bias_constraint=None
)

类似于Conv1D，单卷积核权重不共享

LocallyConnected2D层

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
keras.layers.local.LocallyConnected2D(
	filters,
	kernel_size,
	strides=(1, 1),
	padding="valid",
	data_format=None,
	activation=None,
	use_bias=True,
	kernel_initializer="glorot_uniform",
	bias_initializer="zeros",
	kernel_regularizer=None,
	bias_regularizer=None,
	activity_regularizer=None,
	kernel_constraint=None,
	bias_constraint=None
)

类似Conv2D，区别是不进行权值共享

  • 说明
    • 输出的行列数可能会因为填充方法而改变
  • 例
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    model = Sequential()
    model.add(LocallyConnected2D(64, (3, 3), input_shape=(32, 32, 3)))
    	# apply a 3x3 unshared weights convolution with 64 output filters on a 32x32 image
    	# with `data_format="channels_last"`:
    	# now model.output_shape == (None, 30, 30, 64)
    	# notice that this layer will consume (30*30)*(3*3*3*64) + (30*30)*64 parameters

    model.add(LocallyConnected2D(32, (3, 3)))
    	# now model.output_shape == (None, 28, 28, 32)
    	# add a 3x3 unshared weights convolution on top, with 32 output filters:

Categories

Follow

Recents

Advertisement

follow.it

×