算法分析
基础
算法:一系列解决问题的明确指令,即对于符合一定规范的 输入,能够在有限时间内获得要求的输出
- 算法每步都必须没有歧义
- 必须确定算法所处理的输入的值域
- 同一算法可以用几种不同的形式描述
- 同一问题,可能存在几种不同的算法
- 同问题的不同算法,可能基于不同的解题思路,速度也会不同
算法正确性证明
- 对某些算法,正确性证明十分简单,对于另一些算法,可能十分 复杂
- 证明正确性的一般方法是使用数学归纳法,因为算法的迭代过程 本身就符合其所需的一系列步骤
- 根据特定输入追踪算法操作有意义,但是并不能证明算法的 正确性,只需要一个算法不能正确处理的输入实例就足够了
- 对于近似算法,常常试图证明算法所产生的误差,不超出预定义 的误差
算法分析方向
- 时间效率(time efficiency):算法运行速度
- 空间效率(space efficiency):算法需要多少额外的存储空间
- 简单性(simplicity):取决于审视者的眼光
- 简单的算法更容易理解、实现
- 相应程序包含更少的bug
- 一般性(generality)
- 所解决问题的一般性
- 所接受输入的一般性
- 最优性(optimality):与所解决问题的复杂度有关,与某算法 效率无关
- 是否每个问题都能够用算法的方法来解决
非确定性
Deterministic Alogrithm
确定算法:利用问题解析性质,产生确定的有限、无限序列使其收敛 于全局最优解
依某确定性策略搜索局部极小,试图跳跃已获得的局部极小而 达到某个全局最优点
能充分利用问题解析性质,从计算效率高
Nondeterministic Algorithm
不确定算法,包括两个阶段,将判定问题的实例l作为其输入
- 猜测(非确定)阶段:生成任意串S作为l候选解
- 验证(确定)阶段:把l、S作为输入,,若S是l解输出是, 否则返回否或无法停止
当选仅当对问题每个真实例,不确定算法会在某次执行中 返回是时,称算法能求解此问题
即要求不确定算法对某个解至少能够猜中一次、验证正确性, 同时不应该将错误答案判定为是
Nondeterministic Polynominal Algorithm:验证阶段时间 效率是多项式级的不确定算法
分析框架
- time complexity:算法运行速度
- space complexity:算法需要的额外空间
- 算法需要的额外空间已经不是需要重点关注的问题
影响因素
输入规模$n$
几乎所有算法,对规模更大的输入需要运行更长时间,因此使用 输入规模作为参数很有价值
在有些情况下,选择不同的参数表示输入规模有差别
选择输入规模的度量单位还受到算法的操作细节影响
和数字特性相关的算法,倾向于使用$n$的二进制位数 $b=\lfloor {log_{2}^{n}} \rfloor + 1$
其他因素
有些算法的运行时间不仅取决于输入规模,还取决于特定输入的细节
- worst-case efficiency:最坏情况下的效率
- best-case efficiency:最优情况下的效率
- average-case efficiency
- 平均效率的研究比最差、优效率研究困难很多
- 可以将输入划分为几种类型,使得对同类实例,算法基本 执行次数相同,推导各类输入的概率分布,得到平均次数
- amortized efficiency:应用于算法对同样的数据结构所执行
的一系列操作
- 有些情况下,算法单次执行时间代价高,但是n次运行的 总运行时间明显优于单次执行最差效率 * n
衡量角度
运行时间
使用时间标准的度量算法程序运行时间缺陷
- 计算机速度
- 程序实现质量
- 编译器
- 计时困难
找到basic operation并计算其运行次数
- 不依赖于其他无关因素
- 对总运行时间贡献最大,不需要统计算法每步操作执行次数
- 如:对排序基本操作为键比较,数学问题则是四则运算, 需要注意除法、乘法、加减法耗时依次减小
时间估计
- $c_{op}$:特定计算一个基本操作的执行时间
- $C(n)$:算法执行基本操作的次数
- $T(n)=c_{op}C(n)$:可以用于估算算法的执行时间
- 需要小心使用
- $C(n)$不包含非基本操作的信息,也只是估计的结果
- $c_{op}$也是不可靠的估计值
Order of Growth
小规模输入运行时间差别不足以将高效算法与低效算法相区别, 对大规模输入忽略乘法常量,仅关注执行次数的order of growth 及其常数倍,即算法的渐进效率
按照算法渐进效率进行分类的方法缺乏使用价值,因为没有指定 乘法常量的值
但是对于实际类型输入,除了少数算法,乘法常量之间不会相差 悬殊,作为规律,即使是中等规模的输入,属于较优渐进 效率类型的算法也会比来自较差类型的算法效果好
对数函数:增长慢,以至于可以认为,对数级操作次数的算法能 瞬间完成任何实际规模输入
- 指数级:指数函数、阶乘函数
- 需要指数级操作次数的算法只能用于解决规模非常小的问题
渐进效率
渐进符号
$O(g(n))$
对于足够大的n,$t(n)$的上界由$g(n)$的常数倍确定,则 $t(n) \in O(g(n))$
即存在大于0的常数$c$、非负整数$n_{0}$,使得
增长次数小于等于$g(n) n \rightarrow \infty$ (及常数倍)的函数集合
$\Omega (g(n))$
对于足够大的n,$t(n)$的下界由$g(n)$的常数倍确定,则 $t(n) \in \Omega(g(n))$
即存在大于0的常数$c$、非负整数$n_{0}$,使得
增长次数大于等于$g(n) n \rightarrow \infty$ (及常数倍)的函数集合
$\Theta (g(n))$
对于足够大的n,$t(n)$的上、下界由$g(n)$的常数倍确定,则 $t(n) \in \Theta(g(n))$
即存在大于0的常数$c{1}, c{2}$、非负整数$n_{0}$,使得
增长次数等于$g(n) n \rightarrow \infty$(及常数倍) 的函数集合
极限比较增长次数
利用极限比较增长次数:比直接利用定义判断算法的增长次数方便, 可以使用微积分技术计算极限
基本渐进效率类型
| 类型 | 名称 | 注释 |
|---|---|---|
| $1$ | 常量 | 很少,效率最高 |
| $log_{n}$ | 对数 | 算法的每次循环都会消去问题规模的常数因子,对数算法不可能关注输入的每个部分 |
| $n$ | 线性 | 能关注输入每个部分的算法至少是线性运行时间 |
| $nlog_{n}$ | 线性对数 | 许多分治算法都属于此类型 |
| $n^{2}$ | 平方 | 包含两重嵌套循环的典型效率 |
| $n^{3}$ | 立方 | 包含三重嵌套循环的典型效率 |
| $2^{n}$ | 指数 | 求n个元素的所有子集 |
| $n!$ | 阶乘 | n个元素集合的全排列 |
算法的数学分析
非递归算法
分析通用方案
- 决定表示输入规模的参数
- 找出算法的基本操作:一般位于算法最内层循环
- 检查算法基本操作执行次数是否只依赖于输入规模,如果和其他 特性有关,需要分别研究最差、最优、平均效率
- 建立算法基本操作执行次数的求和表达式(或者是递推关系)
- 利用求和运算的标准公式、法则建立操作次数的闭合公式,或 至少确定其增长次数
递归算法
用一个方程把squence的generic term和一个或多个其他项相关联, 并提供第一个项或前几项的精确值
- recurrence:递推式
- initial condition:序列起始值、递归调用结束条件
- 求解:找到序列通项的精确公式满足递推式、初始条件,或者 证明序列不存在
- general solution:满足递推方程所有解序列公式,通常 会包含参数
- particular solution:满足给定递推方程的特定序列,通常 感兴趣的是满足初始条件的特解
递归求解方法
method of forward substituion:从序列初始项开始,使用 递推方程生成给面若干项,从中找出能用闭合公式表示的模式
- 带入递推方程、初始条件验证
- 数学归纳法证明
method of backward subsitution:从序列末尾开始,把序列 通项$x(n)$表示为$x(n-i)$的函数,使得i是初始条件之一, 再求和公式得到递推式的解
second-order linear recurrence with constant coefficients :求解characteristic equation得到特征根得到通解
常见递推类型
decrease-by-one
减一法:利用规模为n、n-1的给定实例之间的关系求解问题
- 减常数法特例
decrease-by-a-constant-factor
减常因子法:把规模为n的实例化简为规模为n/b的实例求解问题
divide-and-conquer
分治法:将给定实例划分为若干较小实例,对每个实例递归求解,如有必要, 再将较小实例的接合并为给定实例的一个解
平滑法则、主定理
eventually nondecreaing:$f(n)$在自然数上非负,若 $\exists n{0}, \forall n{2} > n{1} \geqslant n{0}, f(n{2}) > f(n{1})$, 则为最终非递减
smooth:$f(n)$在自然数上非负、最终非递减,若 $f(2n) \in \Theta(f(n))$,则平滑
- 若$f(n)$平滑,则对任何整数b有$f(bn) \in \Theta(f(n))$
平滑法则
$T(n)$最终非递减,$f(n)$平滑,若$n=b^{k}(b>2)$时有 $T(n) \in \Theta(f(n))$,则$T(n) \in \Theta(f(n))$
主定理
- 方便对分治法、减常因子法效率进行分析
$T(n)$最终非递减,满足递推式
若$f(n) \in \Theta(n^{d}), d \geqslant 0$,则
分析通用方案
- 决定衡量输入规模的参数
- 找出算法基本操作
- 检查算法基本操作执行次数是否只依赖于输入规模,如果和其他 特性有关,需要分别研究最差、最优、平均效率
- 建立算法基本操作执行次数的递推关系、相应初始条件
- 求解递推式,或至少确定其增长次数
算法时间效率极限
确定已知、未知算法效率极限
算法下界
算法下界是问题可能具有的最佳效率
可以用于评价某问题具体算法效率
- 不同问题算法直接比较无意义
寻找问题的更优算法时,可以根据算法下界确定期望获得的改进
- 若算法下界是紧密的,则改进至多不过是常数因子
- 若算法下界和算法仍有差距,则可能存在更快算法,或者是 证明更好的下界
Trivial Lower Bound
平凡下界:任何算法只要要“读取”所有要处理的项、“写”全部 输出,对其计数即可得到平凡下界
往往过小,用处不大
确定问题中所有算法都必须要处理的输入也是个障碍
例
生成n个不同项所有排列的算法$\in \Omega(n!)$,且下界 是紧密的,因为好的排列算法在每个排列上时间为常数
计算n次多项式值算法至少必须要处理所有系数,否则改变 任意系数多项式值改变,任何算法$\in \Omega(n)$
计算两个n阶方阵乘积算法$\in Omega(n^2)$,因为任何 算法必须处理矩阵中$2n^2$个元素
Information-Theoretic Lower Bound
信息论下界:试图通过算法必须处理的信息量(比特数)建立 效率下界
例
- 猜整数中,整数的不确定信息量就是 $\lceil \log_2 n \rceil$(数字二进制位数), n为整数上界
Adversary Lower Bound
敌手下界:敌手基于恶意、一致的逻辑,迫使算法尽可能多执行, 从而确定的为了保证算法正确性的下界
- 恶意使得它不断把算法推向最消耗时间的路径
- 一致要求它必须和已经做出的选择保持一致(按照一定规则)
例
猜整数中,敌手把1~n个数字作为可选对象,每次做出判断 后,敌手保留数字较多集合,使得最消耗时间、不违背之前 选择
两个有序列表${a_i}, {b_j}$归并排序中,敌手使用规则: 当前仅当i < j时,对$a_i < b_j$返回真(设置列表值大小 可以达到),则任何算法必须比较2n-1次,否则交换未比较 元素归并错误
问题化简
问题Q下界已知,考虑将问题Q转换为下界未知问题P,得到P下界
- 应该表明任意Q问题实例可以转换为P问题
- 即问题Q应该是问题P的子集,正确的算法至少应该能解决Q问题
许多问题复杂性不清楚,而对问题复杂度的直观判断和问题表现 形式相关,并不可靠
常在问题化简中使用的已知下界问题
|问题|下界|紧密性| |——-|——-|——-| |排序|$\Omega(nlogn)$|是| |有序数组查找|$\Omega(logn)$|是| |元素惟一性|$\Omega(nlogn)$|是| |n位整数乘法|$\Omega(n)$|未知| |n阶方程点乘|$\Omega(n^2)$|未知|
例
欧几里得最小生成树:使用元素唯一性问题作为下界已知 问题
- 将n个实数映射为x轴上的n个点
- 设T为此点集最小生成树,T必然包含一条最短边??#todo
- 检查T是否包含长度为0的边即为元素惟一性
任意矩阵A、B乘法:使用方阵乘法作为下界已知问题
将A、B化成对称方阵进行计算
乘积AB可以方便提取,而翻倍的矩阵乘法不会影响复杂性
决策树(二叉)
可以使用(二叉)决策树研究基于比较的算法性能
每个非叶子节点代表一次键值比较
叶子节点个数大于等于输出,不同叶子节点可以产生相同输出
对于特定规模为n的输入,算法操作沿着决策树一条从根到叶子 节点完成,所以最坏情况下比较次数等于算法决策树高度
如果树具有由输出数量确定叶子,则树必须由足够高度容纳叶子 ,即对于任何具有$l$个叶子,树高度 $h \leqslant \lceil log_2 l \rceil$,这也就是 信息论下界
线性表排序
任意n个元素列表排序输出数量等于$n!$,所以任何基于比较的排序 算法的二叉树高度,即最坏情况下比较次数
归并排序、堆排序在最坏情况下大约必须要做$nlog_2n$次比较 ,所以其渐进效率最优
也说明渐进下界$\lceil log_2n! \rceil$是紧密的 ,不能继续改进
但这个只是基于二叉决策树的渐进下界,对于具体值估计 可能不准
如$\lceil log_2 12! \rceil = 29$,而事实证明 12个元素排序30次比较是必要、充分的
也可以使用决策树分析基于比较的排序算法的平均性能,即 决策树叶子节点平均深度
基于排序的所有输出都不特殊的标准假设,可以证明平均 比较次数下界$C_{avg}(n) \geqslant log_2n!$
这个平均是建立在所有输出都不特殊假设上,所以这个其实 应该是不同算法平均比较次数下界的上界
对于单独排序算法,平均效率会明显好于最差效率
有序线性表查找
有序线性表查找最主要算法是折半查找,其在最坏情况下下效率 $C{worst}^{bs} = \lfloor log_2n \rfloor + 1 = \lceil log(n+1) \rceil$
折半查找使用的三路比较(小于、等于、大于),可以使用 三叉查找树表示
三叉查找树会有2n+1个节点:n个查找成功节点、n+1个查找 失败节点
所以在最坏情况下,比较次数下界 $C_{worst}(n) \geqslant \lceil log_3{2n+1} \rceil$ 小于折半查找最坏情况下比较次数(渐进)
然而,事实上可以删除三叉查找树中间子树(等于分支),得到 一棵二叉树
非叶子节点同样表示三路比较,只是同时作为查找成功终点
可以得到一个新的下界 $C_{worst}(n) \geqslant \lceil log_2{n+1} \rceil$
更复杂的分析表明,标准查找假设下,折半查找平均情况比较 次数是最少的
- 查找成功时$log_2n - 1$
- 查找失败时$log_2(n+1)$
P、NP、完全NP问题
复杂性理论
如果算法的最差时间效率$\in O(p(n))$,$p(n)$为问题输入 规模n的多项式函数,则称算法能在多项式时间内对问题求解
Tractable:易解的,可以在多项式时间内求解的问题
Intractable:难解的,不能在多项式内求解的问题
使用多项式函数理由
无法保证在合理时间内对难解问题所有实例求解,除非问题实例 非常小
对实用类型的算法而言,其多项式次数很少大于3,虽然多项式 次数相差很大时运行时间也会有巨大差别
多项式函数具有方便的特性
- 多项式加和、组合也为多项式
多项式类型可以发展出Computational Complexity利用
- 该理论试图对问题内在复杂性进行分类
- 只要使用一种主要计算模型描述问题,并用合理编码方案 描述输入,问题难解性都是相同的
Decision Problem
判定问题:寻求一种可行的、机械的算法,能够对某类问题在有穷 步骤内确定是否具有某性质
Undecidable问题:不可判定问题,不能使用任何算法求解的 判定问题
- 停机问题:给定程序、输入,判断程序对于输入停止还是 无限运行下去
Decidable问题:可判定问题,能用算法求解的问题
可判定、难解问题存在,但非常少
很多判定问题(或者可以转化为等价判定问题),既没有 找到多项式类型算法,也没有证明这样算法不存在,即无法 判断是否难解
P、NP问题
P问题
Polynomial类型问题
非正式定义:易解的问题,即能够在多项式时间内求解的 问题(计算机范畴)
正式定义:能够用确定性算法在多项式时间内求解的 判定问题
多项式时间内求解:排除难解问题
判定问题:很多重要问题可以化简为更容易研究的判断问题 ,虽然原始表达形式不是判定问题
NP问题
Nondeterministic Polynomial类型问题:可以用不确定多项式 算法求解的判定问题
NP问题虽然计算上对问题求解困难,但是在计算上判定待定结 是否解决问题是简单的:可以在多项式时间内完成
大多数判断问题都是属于NP类型的
$P \subseteq NP$:如果问题属于P,在不确定算法验证 阶段忽略猜测
还包括以下没有找到多项式算法、也没有证明算法不存在 的组合优化问题的判定版本
- 哈密顿回路问题
- 旅行商问题
- 背包问题
- 划分问题
- 装箱问题
- 图着色问题
- 整数线性规划问题
$P \overset ? = NP$:P和NP问题是否一致,计算机科学理论 中最重要的未解之谜
- P = NP意味着虽然没有找到,但能够在多项式时间内求解 许多组合优化问题确实存在
NPC问题
NP Complete问题
- 属于NP问题种,和该类型其他问题难度一致
- 证明问题属于NP问题比较简单
- NP中其他任何问题(已知或未知)可以在多项式时间内化简为 NPC问题
直接证明任何NP问题都可以在多项式时间内化简为当前问题 比较困难
常常利用多项式规约特性,证明某个确定NPC问题可以 多项式规约为当前问题
判定问题相互转换例
- 哈密顿回路问题中图G映射加权图$G^{‘}$,G中存在边在 权重为1,不存在边权重为2,则哈密顿回路问题转换为$G^{‘}$ 是否存在长度不超过$|V|$的哈密顿回路,即旅行商问题的等价
NPC问题案例
CNF-Satisfied Problem:合取范式可满足性问题,首个 被发现NPC问题
前面提到的著名NP问题都是NPC问题
- 包括哈密顿回路问题???
仅仅得到一个NPC问题的多项式确定算法,所有NP问题可以 在多项式时间内求解
则$P = NP$
即对于所有类型判定问题而言,检验待定解、在多项式时间 内求解在复杂性商没有本质区别
而NPC问题可以被其他NP问题转换而来意味着,NPC问题目前不 存在对所有实例通用的多项式时间算法
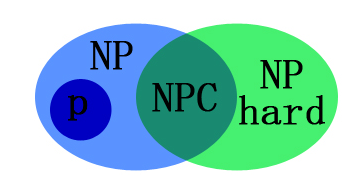
NP-Hard问题
NP-Hard问题:所有NP问题都可以通过多项式规约到其
不满足NPC问题第一个条件,可以不是NP问题
其范围包含NPC问题,前述组合优化问题最优版本也是NP-Hard
可以理解为:至少和NPC问题一样困难的问题
Reference
Polynomially Reducible
判定问题$D_1$可以多项式规约为判定问题$D_2$,条件是存在 函数t可以把$D_1$的实例转换为$D_2$的实例,满足
t把$D_1$所有真实例映射为$D_2$真实例,把$D_1$所有假实例 映射为$D_2$假实例
t可以用多项式算法计算
CNF-Satisfied Problem
合取范式满足性问题:能否设置合取范式类型的布尔表达式中布尔 变量值,使得整个表达式值为真
- 每个布尔表达式都可以表达为合取范式

