Posted 2021-07-12Updated 2021-07-19Math Mixin / Statisticsa few seconds read (About 111 words)

统计量

统计量：统计理论中对数据进行分析、检验的变量

传统的统计量具有显式解析表达式
- 均值：数据之和除数量
- 中位数：数据中间者
统计量同样可以理解为和数据相关优化问题的解
- 均值：离差平方和最小
- 中位数：划分均匀
- 优化问题目标本身也是统计量

Posted 2021-07-12Updated 2021-07-12Math Mixin / Statistics7 minutes read (About 1069 words)

统计量 - 衍生特征

Odds/Odds Ratio

Odds：几率/优势，事件发生与不发生的概率比值
- $p$：事件发生概率
Odds Ratio：优势比，两组事件 odds 的比值
$OR = \frac {odds_1} {odds_0}$

WOE 值

WOE 值：将预测变量（二分类场景中）集中度作为分类变量编码的数值

$\begin{align*} WOE_i & = log(\frac {\%B_i} {\%G_i}) \\ & = log(\frac {\#B_i / \#B_T} {\#G_i / \#G_T}) \\ & = log(\frac {\#B_i / \#G_i} {\#B_T / \#G_T}) \\ & = log(\frac {\#B_i} {\#G_i}) - log(\frac {\#B_T} {\#G_T}) \\ & = log(\frac {\#B_i / ({\#B_i + \#G_i})} {\#G_i / (\#B_i + \#G_i)}) - log(\frac {\#B_T} {\#G_T}) \\ & = log(odds_i) - log(odds_T) \end{align*}$

$\%B_i, \%G_i$：分类变量取第 $i$ 值时，预测变量为 B 类、G 类占所有 B 类、G 类比例

$#B_i, #B_T$：分类变量取第 $i$ 值时预测变量为 B 类数量，所有 B 类总数量

$#G_i, #G_T$：分类变量取第 $i$ 值时预测变量为 G 类数量，所有 G 类样本总数量

$odds_i$：分类变量取第 $i$ 值时，预测变量取 B 类优势

$odds_T$：所有样本中，预测变量取 B 类优势

其中 $log$ 一般取自然对数

WOE 编码是有监督的编码方式，可以衡量分类变量各取值中
- B 类占所有 B 类样本比例、G 类占所有 G 类样本比例的差异
- B 类、G 类比例，与所有样本中 B 类、G 类比例的差异
WOE 编码值能体现分类变量取值的预测能力，变量各取值 WOE 值方差越大，变量预测能力越强
- WOE 越大，表明该取值对应的取 B 类可能性越大
- WOE 越小，表明该取值对应的取 G 类可能性越大
- WOE 接近 0，表明该取值预测能力弱，对应取 B 类、G 类可能性相近

OR与WOE线性性

$\begin{align*} log(OR_{j,i}) &= log(odds_i) - log(odds_j) \\ &= WOE_i - WOE_j \end{align*}$

即：预测变量对数优势值与 WOE 值呈线性函数关系
- 预测变量在取 $i,j$ 值情况下，预测变量优势之差为取 $i,j$ 值的 WOE 值之差
- WOE 值编码时，分类变量在不同取值间跳转时类似于线性回归中数值型变量
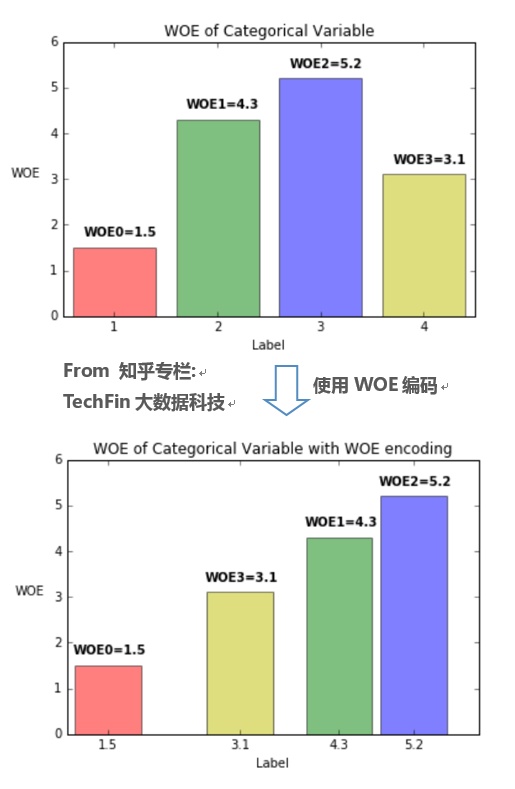
考虑到对数优势的数学形式，单变量 LR 模型中分类型变量 WOE 值可以类似数值型变量直接入模
- 当然，WOE 值编码在多元 LR 中无法保证单变量分类情况下的线性
- 或者说多变量 LR 中个变量系数值不一定为 1
- 在基于单变量预测能力优秀在多变量场合也优秀的假设下，WOE 值编码（IV 值）等单变量分析依然有价值

Bayes Factor、WOE 编码、多元 LR

$\begin{align*} ln(\frac {P(Y=1|x_1,x_2,\cdots,x_D)} {P(Y=0|x_1,x_2,\cdots,x_D)}) &= ln(\frac {P(Y=1)} {P(Y=0)}) \\ & \overset {conditionally independent} {=} ln (\frac {P(Y=1)} {P(Y=0)}) + \sum_{i=1}^D ln(\frac {P(x_i|Y=1)} {P(x_i|Y=0)}) \\ ln(\frac {P(Y=1|x_1,x_2,\cdots,x_D)} {P(Y=0|x_1,x_2,\cdots,x_D)}) & \overset {semi} {=} ln (\frac {P(Y=1)} {P(Y=0)}) + \sum_{i=1}^D \beta_i ln(\frac {P(x_i|Y=1)} {P(x_i|Y=0)}) \end{align*}$

$\frac {P(x_i|Y=1)} {P(x_i|Y=0)}$：贝叶斯因子，常用于贝叶斯假设检验

Naive Bayes 中满足各特征 $X$ 关于 $Y$ 条件独立的强假设下，第二个等式成立
Semi-Naive Bayes 中放宽各特征关于 $Y$ 条件独立假设，使用权重体现变量相关性，此时则可以得到多元 LR 的预测变量取值对数 OR 形式
- 则多元 LR 场景中，WOE 值可以从非完全条件独立的贝叶斯因子角度理解

IV 值

$\begin{align*} IV_i &= (\frac {\#B_i} {\#B_T} - \frac {\#G_i} {\#G_T}) * WOE_i \\ &= (\frac {\#B_i} {\#B_T} - \frac {\#G_i} {\#G_T}) * log(\frac {\#B_i / \#B_T} {\#G_i / \#G_T}) \\ IV &= \sum IV_i \end{align*}$

$IV_i$：特征 $i$ 取值 IV 值

$IV$：特征总体 IV 值

特征总体的 IV 值实际上是其各个取值 IV 值的加权和
- 类似交叉熵为各取值概率的加权和

Posted 2021-07-12Updated 2021-07-12Math Mixin / Statistics16 minutes read (About 2441 words)

统计量 - 熵

Entropy

（信息）熵：在概率分布上对复杂程度/多样性/不确定性/混乱程度的度量

$\begin{align*} HOD(X) & = -E_P log P(x) \\ & = \sum_d^D P(x_d) log \frac 1 {P(x_d)} \\ & = - \sum_d^D p_d log p_d \\ \end{align*}$

$p_d$：随机变量各取值对应概率

事件 $i$ 发生概率 $p_d=0$：约定 $p_d log(p_d)$ 为 0

其中 $log$ 以 2 为底，单位为 bit，以 $e$ 为底，单位为 nat

信息论中，熵越高能传输越多信息
- 可携带的信息量 = 单位消息熵 * 消息长度
- 熵衡量系统复杂程度，提高系统确定性即削弱系统多样性，降低熵
概率分布包含的信息即其复杂程度（可能取值数量）
- 考虑按照 $(p_1,\cdots,p_D)$ 分布、长度为 $N$ 的随机变量序列，其可能排列数为 $\frac {N!} {\prod_d^D (p_d N)!}$
- 则根据 Stirling 公式有
  $\begin{align*} log (\frac {N!} {\prod_d^D (p_d N)!}) & = log(N!) - \sum_d^D log((p_d N)!) \\ & \overset {\lim_{N \rightarrow \infty}} = log(\sqrt {2\pi N} ({\frac N e})^N) + \sum_d^D log(\sqrt {2\pi p_dN} ({\frac {p_dN} e})^{p_dN}) \\ & = log(\sqrt {2\pi N}) + N(logN-1) - \sum_d^D log(\sqrt {2\pi p_dN}) - \sum_d^D p_dN (log(p_dN) - 1) \\ & = log(\sqrt {2\pi N} + \sum_d^D log(\sqrt {2\pi p_dN})) + N \sum_d^D p_d log p_d \\ & \approx N \sum_d^D p_d log p_d \end{align*}$
- 则长度为 $N$ 的随机变量串的多样性、信息量为 $H * N$，其中 $H=\sum_d^D p_d log p_d$ 概率分布的信息熵
某个事件包含的信息可以用编码长度理解
- 对概率 $p$ 事件，编码 $1/p$ 个需编码（2进制编码）长度 $log_2 \frac 1 p$
- 则概率 $p$ 事件包含信息量可以定义为 $log \frac 1 p$，即事件包含的信息量可用表示事件需要编码的长度表示（底数则取决于编码元，只影响系数）
- 则整个随机变量的信息为各事件信息量加权和
熵可以视为变量取值概率的加权和
- 只依赖随机变量 $X$ 的分布，与其取值无关，可将其记为 $H(P)$
- 由定义 $0 \leq H(P) \leq log_2 k$
  - $H(p) = 0$：$\exists j, p_j=1$，随机变量只能取一个值，无不确定性
  - $H(p) = log k$：$\forall j, p_j=1/k$，随机变量在任意取值概率相等，不确定性最大

empirical entropy：经验熵，熵中的概率由数据估计时（尤极大似然估计）

参考链接

https://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)

https://zhuanlan.zhihu.com/p/27876027

https://zhuanlan.zhihu.com/p/73710585

Stirling 公式即用积分近似计算 $\sum logn$：https://zhuanlan.zhihu.com/p/143992660

熵的性质

对称性：事件取值不影响熵
极值性
- 所有符号有同等机会出现的情况下，熵达到极大（琴生不等式）
  $\begin{align*} H(X) & = E[log(\frac 1 {P(X)})] \leq log(E[\frac 1 {P(x)}]) & = log(n) \end{align*}$
- 仅有一个符号确定出现的情况下，熵达到极小 0
Continuity连续性：度量连续，概率微小变化只能引起熵微小变化
Normalization规范化：$H_2(\frac 1 2, \frac 1 2) = 1$
Grouping组合法则/可加和性：熵与过程如何划分无关（此即要求熵形式为对数）
- 若子系统间相互作用已知，则可以通过子系统熵值计算系统整体熵
  - $X_1,\cdots,X_K$：$K$ 个子系统，可以理解为将随机变量 $X$ 划分为 $K$ 种情况
  - $H(X_1,\cdots,X_K)$：子系统相互作用熵
  - 子系统相互作用熵可以认为是，通过已知信息消除的多样性（即信息增益）
  - 子系统熵之和则是利用已知信息消除多样性之后，系统剩余混乱程度
- 一般的，两个事件 $X,Y$ 熵满足以下计算关系
  $\begin{align*} H(X, Y) & = H(X) + H(Y|X) \\ & = H(Y) + H(X|Y) \\ & \leqslant H(X) + H(Y) \\ H(X|Y) & \leqslant H(X) \\ \end{align*}$
- 特别的，若事件 $X, Y$ 相互独立
  $\begin{align*} H(X|Y) &= H(X) \\ H(X, Y) &= H(X) + H(Y) \end{align*}$

满足以上特性的熵定义必然为如下形式

$$
-K \sum P(x)log(P(x))
$$

在热力学、信息论等领域，熵有多种不同定义，满足熵性质的测度泛函，只能具有（Shannon 熵和 Hartley 熵）或（von Neumann 熵和 Shannon 熵）线性组合的函数形式，若不要求满足组合法则，还有 Tsallis 熵等

Conditinal Entropy

条件熵：随机变量 $X$ 给定条件下，随机变量 $Y$ 的条件概率分布的熵对 $X$ 的数学期望

$\begin{align*} H(Y|X) & = \sum_{i=1}^N p_i H(Y|X=x_i) \\ H(Y|x=x_i) & = - \sum_j P(y_j|x_i) log P(y_j|x_i) \end{align*}$

$P(X=xi, Y=y_j)=p{i,j}$：随机变量 $(X,Y)$ 联合概率分布

$p_i=P(X=x_i)$

$H(Y|X=x_i)$：后验熵

特别的，考虑数据集 $D$ 被分为 $D_1,\cdots,D_m$，条件经验熵可计算如下
$\begin{align*} H(D|A) & = \sum_{m=1}^M \frac {|D_m|} {|D|} H(D_m) \\ & = -\sum_{m=1}^M \frac {|D_m|} {|D|} \sum_{k=1}^K \frac {|D_{m,k}|} {|D_m|} log_2 \frac {|D_{m,k}|} {|D_m|} \end{align*}$

postorior entropy：后验熵，随机变量 $X$ 给定条件下，随机变量 $Y$ 的条件概率分布的熵

empirical conditional entropy：经验条件熵，概率由数据估计

Infomation Gain/Mutual Infomation

互信息/信息增益：（经验）熵与（经验）条件熵之差

$\begin{align*} g(Y|X) & = H(Y) - H(Y|X) \\ & = \sum_{x \in X} \sum_{y \in Y} P(x,y) log \frac {P(x,y)} {P(x)P(y)} \end{align*}$

与数据集具体分布有关、与具体取值无关
- 绝对大小同易受熵影响，（经验）熵较大时，互信息也相对较大
- 由于误差存在，分类取值数目较多者信息增益较大
可衡量变量 $X$ 对 $Y$ 预测能力、减少不确定性的能力
- 信息增益越大，变量之间相关性越强，自变量预测因变量能力越强
- 只能考察特征对整个系统的贡献，无法具体到特征某个取值
- 只适合作全局特征选择，即所有类使用相同的特征集合

Infomation Gain Ratio

信息增益比：信息增益对原始信息熵的比值

$\begin{align*} g_R(Y|X) & = \frac {g(Y|X)} {H(X)} \end{align*}$

考虑熵大小，减弱熵绝对大小的影响

Cross Entropy

信息论：基于相同事件测度的两个概率分布 $P, Q$，基于非自然（相较于真实分布 $P$）概率分布 $Q$ 进行编码，在事件集合中唯一标识事件所需 bit

概率论：概率分布 $P, Q$ 之间差异

$\begin{align*} H(P, Q) & = E_P[-log Q] = \left \{ \begin{array}{l} -\sum_{X} P(x) logQ(x), & 离散分布 \\ -\int_X P(x) log(Q(x)) d(r(x)), & 连续分布 \end{array} \right. \\ & = H(P) + D_{KL}(P||Q) \end{align*}$

$P(x), Q(x)$：概率分布（密度）函数

$r(x)$：测度，通常是 $Borel \sigma$ 代数上的勒贝格测度

$D_{KL}(P||Q)$：$P$ 到 $Q$ 的 KL 散度（$P$ 相对于 $Q$ 的相对熵）

信息论中，交叉熵可以看作是信息片段在错误分布 $Q$ 分布下的期望编码长度
- 信息实际分布实际为 $P$，所以期望基于 $P$

交叉熵是常用的损失函数：效果等价于 KL 散度，但计算方便

sigmoid 激活函数时：相较于二次损失，收敛速度更快

Entropy 衍生指标

Kullback-Leibler Divergence

KL 散度/相对熵：衡量概率分布 $P, Q$ 之间差异的量化指标

$\begin{align*} D_{KL}(P||Q) & = E_P[(-log Q(x)) - (-log P(x))] \\ & = E_P[log P(x) - log Q(x)] \\ & = \sum_{d=1}^D P(x_d) (log P(x_d) - log Q(x_d)) \\ & = \sum_{d=1} P(x_d) log \frac {P(x_d)} {Q(x_d)} \end{align*}$

KL 散度含义
- 原始分布 $P$、近似分布 $Q$ 之间对数差值期望
- 若使用观察分布 $Q$ 描述真实分布 $P$，还需的额外信息量
KL 散度不对称，分布 $P$ 度量 $Q$、$Q$ 度量 $P$ 损失信息不同
- 从计算公式也可以看出
- KL散度不能作为不同分布之间距离的度量

Population Stability Index

PSI：衡量分布 $P, Q$ 之间的差异程度

$\begin{align*} PSI &= \sum_d^D (P_d - Q_d) * log \frac {P_d} {Q_d} \\ &= \sum_d^D P_d log \frac {P_d} {Q_d} + \sum_d^D Q_d log \frac {Q_d} {P_d} \\ &= D_{KL}(P||Q) + D_{KL}(Q||P) \end{align*}$

是 KL 散度的对称操作
- 更全面的描述两个分布的差异

Gini 指数

基尼指数：可视为信息熵的近似替代

$\begin{align*} Gini(p) & = \sum_{k=1}^K p_k(1-p_k) \\ & = 1 - \sum_{k=1}^K p_k^2 \end{align*}$

$p$：概率分布

异质性最小：Gini 系数为 0

异质性最大：Gini 系数为 $1 - \frac 1 k$

Gini 指数度量分布的不纯度
- 包含类别越多，Gini 指数越大
- 分布越均匀，Gini 指数越大

熵较 Gini 指数对不纯度判罚更重

gini_entropy_error_rate_in_binary_classification

经济学领域的 Gini 系数更类似 AUC 值

与 Entropy 关系

$\begin{align*} H(X) & = -E_P log P(x) \\ & = - \sum_i^N p_i log p_i \\ & = - \sum_i^N p_i (log (1 + (p_i-1))) \\ & = - \sum_i^N p_i (p_i - 1 + \xi(p_i^{'}-1)) \\ & \approx 1 - \sum_i^N p_i^2 \end{align*}$

Gini 指数可以视为是熵在 1 附近的一阶泰勒展开近似

条件 Gini 指数

$Gini(Y|X) = \sum_{k=1}^K P(X=x_k)Gini(Y|X=x_k)$

性质类似信息增益

Posted 2021-07-12Updated 2021-07-12Math Mixin / Statistics9 minutes read (About 1370 words)

统计量 - 相关

Pearson 积矩相关系数

$\rho_{X,Y} = \frac {cov(X, Y)} {\sigma_X \sigma_Y}$

$cov(X, Y)$：变量 $X, Y$ 协方差

$\sigma_X, \sigma_Y$：变量 $X, Y$ 方差

Pearson 积矩相关系数取值范围为 $[-1, 1]$
- $1, -1$ 分别表示变量成正线性、负线性函数关系

显著性检验

Fisher 变换

$z = \frac 1 2 ln(\frac {1+r} {1-r}) = arctanh(r)$

$z$：Pearson 积矩相关系数的 Fisher 变换

$r$：样本的 Pearson 积矩相关系数值

当 $(X, Y)$ 为二元正态分布时，$z$ 近似正态分布
- 均值：$\frac 1 2 ln(\frac {1+\rho} {1-\rho})$
- 标准差：$\frac 1 {\sqrt {N - 3}}$

基于数学的近似方法

$t = r \sqrt{\frac {N - 2} {1 - r^2}}$

当 $(X, Y)$ 为二元正态分布且不相关时，$t$ 服从自由度为 $n-2$的 t-分布

Spearman 秩相关系数

$\begin{align*} \rho_{X, Y} & = \frac {cov(Rank(X) - Rank(Y))} {\sigma_{Rank(X)} \sigma_{Rank(Y)}} \\ & = 1 - \frac {6 \sum_i^N d_i^2} {N(N^2-1)} \\ \end{align*}$

$Rank(X), Rank(Y)$：变量 $X, Y$ 的秩（应同序）（相同值秩取均值）

$d_i$：变量对 $X, Y$ 中，二者秩差值

Spearman 秩相关系数被定义为变量秩的 Pearson 相关系数

Spearman 秩相关系数也可以使用 Fisher 变换检验显著性

Kendell 秩相关系数

$\begin{align*} \tau_a &= \frac {N_c - N_d} {N_0} \\ \tau_b &= \frac {N_c - N_d} {\sqrt{(N_0 - N_X)(N_0 - N_Y)}} \\ \tau_c &= \frac {2(N_c - N_d)} {N^2 \frac {M-1} M} \end{align*}$

$N_0 = \frac {N(N-1)} 2$：变量对数量

$N_c, N_d$：变量对 $X, Y$ 中有序对数量、无序对数量

$N_X, N_Y$：变量对 $X, Y$ 中 $X$ 取值、$Y$ 取值相同对数量

$M$：变量 $X, Y$ 中较小取值数量者取值数量

Kendell 秩相关系数取值范围同样为 $[-1, 1]$
- -1 仅在变量 $X, Y$ 取值完全反向取到
$\tau_a$ 是 $\tau_b$ 在变量不存在取值相同时的特例
$\tau_c$ 适合“层级”数据，即两个变量取值类似划分、内部细分

||A|B|C| |——-|——-|——-|——-| |I-1|30|0|0| |I-2|30|0|0| |II-1|0|30|0| |II-1|0|30|0| |III-2|0|0|30| |III-2|0|0|30|
- 对以上数据，$\tau_b$ 取值在 0.9 附近，而 $\tau_c$ 取 1

有序对：对 $(X_i, Y_i), (X_j, Y_j)$，满足 $X_i < X_j, Y_i < Y_j$ 或 $X_i > X_j,Y_i > Y_j$ 则为有序对

无序对：对$(X_i, Y_i), (X_j, Y_j)$，满足 $X_i < X_j, Y_i > Y_j$ 或 $X_i > X_j, Y_i < Y_j$ 则为无序对

卡方统计量

卡方统计量：通过观察实际与理论值的偏差确定理论正确与否

$\chi^2 = \sum \frac {(A - E)^2} E$

$A$：自变量、因变量组合对应频数观察值

$E$：自变量、因变量组合对应频数期望值

将模型预测结果视为实际分布、先验分布（均匀分布）视为理论分布
卡方检验：检验定性变量之间相关性，假设两个变量确实独立，观察实际值、理论值偏差程度判断变量之间相关性
- 若偏差足够小，认为误差是自然的样本误差，两者确实独立
- 若偏差大到一定程度，误差不可能由偶然、测量精度导致，认为两者相关
若模型预测结果同先验分布差别很大，说明模型有效，且卡方统计量值越大表示预测把握越大

特点

由于随机误差存在，卡方统计量容易
- 夸大频数较小的特征影响
- 相应的，取值数较少（各取值频数相对而言可能较大）特征影响容易被低估

分布证明

考虑随机变量 $X=(x_1,\cdots,x_D)$ 服从 Multinomial 分布，分布参数为 $n, p=(p_1,\cdots,p_D)$
考虑服从理论分布的随机变量 $X$ 协方差矩阵
$\begin{align*} \Sigma = Cov(X) &= \begin{bmatrix} np_1(1-p_1) & -np_1p_2 & \cdots & -np_1p_D \\ np_2p_1 & -np_2(1-p_2) & \cdots & -np_2p_D \\ \vdots & \vdots & \ddots & \vdots \\ -np_Dp_1 & -np_Dp_2 & \cdots & np_D(1-p_D) \end{bmatrix} \\ &= n\begin{bmatrix} p_1 & 0 & \cdots & 0 \\ 0 & p_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & p_D \end{bmatrix} - npp^T \\ \end{align*}$
则由中心极限定理有，如下依分布收敛的结论
$\begin{align*} \frac {(X - np)} {\sqrt n} & \overset {D} {\rightarrow} N(0,\Sigma) \\ \end{align*}$
考虑服从理论分布的随机变量 $X$ 的 $\chi^2$ 参数
$\begin{align*} \chi^2 &= \frac 1 n (X-np)^T D^2 (X-np) \\ D &= \begin{bmatrix} \frac 1 {\sqrt {p_1}} & 0 & \cdots & 0 \\ 0 & \frac 1 {\sqrt {p_2}} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \frac 1 {\sqrt {p_D}} \end{bmatrix} \end{align*}$
并由连续映射定理可以得到 $D\frac {x-np} {\sqrt n}$ 分布，且其协方差矩阵 $\Sigma_0$ 满足
$\begin{align*} D\frac {x-np} {\sqrt n} & \overset {D} {\rightarrow} N(0, D \Sigma D^T) \\ \Sigma_0 &= D \Sigma D^T \\ \Sigma_0^2 &= (E - \sqrt p {\sqrt p}^T)(E - \sqrt p {\sqrt p}^T) = \Sigma_0 \\ \end{align*}$
由以上，$\Sigma_0$ 仅有特征值 0，1
- 特征值 0 对应特征向量有且仅有 $\sqrt p$
- 特征值 1 对应特征向量有 $D-1$ 个
则 $\chi^2$ 统计量依分布收敛于自由度为 $D-1$ 的卡方分布
$\begin{align*} \chi^2 &= \sum_{d=1}^D \frac {(x_d - np_d)^2} {np_d} \overset {D} {\rightarrow} \chi_{D-1} \end{align*}$
可据此构造统计量进行卡方检验，检验实际值实际分布频率 $(a_1,\cdots,a_D)$ 是否符合该分布
- 构造卡方统计量 $\chi^2 = \sum_{d=1}^D \frac {(x_d - na_d)^2} {na_d}$
- 则卡方统计量在随机变量满足多项分布情况下依分布收敛于自由度为 $D-1$ 的卡方分布

https://www.zhihu.com/question/309694332/answer/952401910

https://zhuanlan.zhihu.com/p/198864907

Posted 2019-07-14Updated 2021-08-04Math Mixin / Statistics13 minutes read (About 2022 words)

常用统计量

混淆矩阵

对比实际类别值、预测类别值，编制混淆矩阵
基于混淆矩阵，计算各类错判率、总错判率（总错判率会受到数据不平衡性的影响）

真实情况\预测结果	正例	反例
正例	TP（真正例）	FN（假反例）
反例	FP（假正例）	TN（真反例）

confusion_matrix

F-Measure

F-测度：准率率和召回率综合值，越大越好

$F-measure = \frac {(\beta^2 + 1) * P * R} {\beta^2 * P + R}$

$P = \frac {TP} {TP+FP}$：查准率、精确率

$R = \frac {TP} {TP+FN}$：查全率、召回率、覆盖率

F1 值

F1值：$\beta=1$ 时的 F测度

$\begin{align*} \frac {1} {F_{1}} &= \frac {1} {2} \left( \frac {1} {P} + \frac {1} {R} \right) \\ \Rightarrow F_{1} &= \frac {2 * P * R} {P + R} = \frac {2 * TP} {样例总数 + TP - TN} \end{align*}$

TPR、FPR

TPR、FPR 可视为对 TP、FP 用样本数量归一化的结果
- 样本全体中正、负样本数量往往差距很大，直接比较 TP、FP 不合理
- 考虑使用样本正、负数量归一化，即计算正比例 TPR、负比例 FPR
TPR 越高越好，FPR 越低越好，但是这两个指标相互制约，两者同时增加、减小
- 模型倾向于将样本 判定为 为正例，则 TP、FP 同时增加，TPR、FPR 同时变大
- 即模型取不同阈值，会产生正相关的 TPR、FPR 的点列

Recevier Operating Characteristic Curve

ROC 曲线：不同 正样本概率 划分阈值下 TPR、FPR 绘制的折线/曲线

$TPR = \frac {TP} {TP+FN} \\ FPR = \frac {FP} {FP+TN}$

ROC 曲线即以 FPR 为横坐标、TPR 为正坐标绘制曲线
- FPR 接近 1 时，TPR 也接近 1，这是不可避免的
- 而 FPR 接近 0 时，TPR 越大越好
- 所以模型 ROC 曲线下方面积越大，模型判断正确效果越好
理解
- 将正负样本的正样本概率值分别绘制在 x=1、x=-1 两条直线上
- 阈值即为 y=threshold 直线
- TPR、FPR 则为 x=1、x=-1 两条直线在阈值直线上方点数量，与各直线上所有点数量比值

Accuracy

准确率、误分率：评价分类器性能一般指标

$\begin{align*} acc & = \frac 1 N sign(y_i = \hat y_i) \\ & = \frac {TP+TN} N \\ mis & = 1 - acc \end{align*}$

$y_i$：第 $i$ 样本实际类别

$\hat y_i$：第 $i$ 样本预测类别

$N$：样本数量

对给定测试集，分类器正确分类样本数与总样本数比值
即 0-1 损失函数时经验风险

Top PR

头部准召：评估模型头部性能

$pr_{top} = \frac {TP_{top}} {TOP}$

$TOP$：指定的头部数量

$TP_{top}$：头部中正例数量（正例指已知原 $TOP$ 样本）

Area Under Curve

AUC 值：ROC 曲线下方面积，越大越好

AUC 值实际含义：随机抽取一对正、负样本，对其中正样本的正样本预测概率值、大于负样本的正样本预测概率值的概率
- $=1$：完美预测，存在一个阈值可以让模型 TPR 为 1，FPR 为 0
- $(0.5, 1)$ ：优于随机预测，至少存在某个阈值，模型 $TPR > FPR$
- $=0.5$：同随机预测，无价值
- $[0, 0.5)$：差于随机预测，但是可以反向取预测值

AUC 计算

绘制 ROC 曲线，计算曲线下面积
- 给定一系列阈值（最精确时为样本数量），分别计算 TPR、FPR
- 根据 TPR、FPR 计算 AUC
正负样本分别配对，计算正样本预测概率大于负样本比例
- $M, N$：正、负样本数量
Mann-Witney U 检验：即正、负样本分别配对的简化公式
- $Pos$：正样本集合
- $rank(i)$：样本 $i$ 的按正样本概率排序的秩（对正样本概率值相同样本，应将秩加和求平均保证其秩相等）

Weighted-AUC

WAUC：给 每个样本 赋权，计算统计量时考虑样本权重

FPR、TPR 绘图
- $WTPR, WFPR$：加权 TPR、加权 FPR
- $\hat y_i$：样本预测类别
- $w_i$：样本权重
Mann-Witney U 检验：考虑其意义，带入权重即可得
- $rank_{pos}(i)$：正样本内部排序，样本$i$秩
- $Neg$：负样本集合

多分类 AUC

Micro-AUC：将每个类别视为样本标签，计算全体样本的正标签、负标签的 AUC

$n$ 个样本的 $m$ 维标签展平，则其中有 $n$ 个正样本、$n * (m-1)$ 个负样本
$n$ 个样本的 $m$ 个分类器共 $n * m$ 个得分展平
使用以上预测得分、标签计算 AUC

# one-vs-rest分类器得分
y_score = classifer.transform(X_test)
# 展平后计算fpr、tpr
fpr_micro, tpr_micro, threshhold_micro = \
	skilearn.metrics.roc_curve(y_test.ravel(), y_score.ravel())
# 利用fpr、tpr计算auc
auc_micro = skilearn.metrics.auc(fpr_micro, tpr_micro)

# 等价于直接调用
auc_micro = skilearn.metrics.roc_auc_score(y_test, y_score, average="micro")

Macro-AUC：对各类别，分别以计算 ROC 曲线（即 TPR、FPR），计算平均 ROC 曲线得到 AUC

对各类别分别计算 TPR、FPR，共 $m$ 组 TPR、FPR

平均合并 TPR、FPR，计算 AUC

方法1：合并 FPR、去除重复值，使用 $m$ 组 TPR、FPR 分别求合并后 FPR 插值

# 分别计算各类别fpr、tpr
fprs, tprs = [0] * n_classes, [0] * n_classes
for idx in range(n_classes):
	fprs[idx], tprs[idx], _ = sklearn.metrics.ruc_curve(
		y_test[:, i], y_score[:, i])
# 合并fpr
all_fpr = np.unique(np.concatenate(fprs))
mean_tpr = np.zeros_like(all_fpr)
# 计算合并后fpr插值
for idx in range(n_classes):
	mean_tpr += scipy.interp(all_fpr, fpr[idx], tpr[idx])
mean_tpr /= n_classes
auc_macro = sklearn.metrics.auc(all_fpr, mean_tpr)

# 但是和以下结果不同
auc_macro = sklearn.metrics.roc_auc_score(fprs)

以上分类器均为 one-vs-rest 分类器，$m$ 个类别则 $m$ 个分类器、每个样本 $m$ 个得分

Kolmogorov-Smirnov 统计量

KS 值：刻画区分正负样本能力

$KS = max \{|TPR - FPR|\}$

KS 值体现 最理想情况 下，对正负样本区分能力
- 即 ROC 曲线与 $TPR = FPR$ 直线的最远距离

Squared Error

Mean Squared Error

MSE：均方误差（偏差）

$MSE = \frac 1 n \sum_{i=1}^{n} (y_{i} - \hat{y_{i}})^{2}$

Mean Absolute Error

MAE：平均绝对误差

$MAE = \frac 1 n \sum_{i=1}^n |y_i - \hat {y_i}|$

Mean Absolute Percentage Error

MAPE：平均绝对百分比误差

$MAPE = \frac 1 n \sum_{i=1}^n |\frac {y_i - \hat {y_i}} {y_i}|$

Symmetric Mean Absolute Percentage Error

SMAPE：对称平均绝对百分比误差

$MAPE = \frac 1 n \sum_{i=1}^n |\frac {y_i - \hat {y_i}} {(|y_i| + |\hat {y_i}|) / 2}|$

$R^2$

$\begin{align*} R^2 & = 1 - \frac {SSE} {SST} = \frac {SSR} {SST} \\ R^2_{adj} & = 1 - \frac {1 - R^2} {n - p - 1} \end{align*}$

$n, p$：样本量、特征数量

$SSE$：残差平方和

$SSR$：回归平方和、组内平方和

$SST$：离差平方和

$R^2_{adj}$：调整的$R^2$

Akaike Information Criterion

AIC ：赤池信息准则

$\begin{align*} AIC & = -2log(L(\hat \theta, x)) + 2p \\ & = nln(SSE/n) + 2p \end{align*}$

$n, p$：样本量、特征数量

$\theta$：带估参数

$L(\theta, x)$：似然函数

$SSE$：残差平方和

Bayesian Information Criterion

BIC：贝叶斯信息准则

$\begin{align*} BIC & = -2log(L(\hat \theta, x)) + ln(n)p \\ & = nln(SSE/n) + ln(n)p \end{align*}$

$C_p$

$\begin{align*} C_p & = \frac {SSE} {\hat {\sigma^2}} - n + 2p \\ & = (n - m - 1) \frac {SSE_p} {SSE_m} - n + 2p \end{align*}$

$p$：选模型特征子集中特征数量

$m$：所有特征数量

$SSE_p$：选模型中残差平方和

$SSE_m$：全模型中残差平方和

统计量

统计量