Feature Selection

特征选择：从特征集合中选择最具统计意义的特征子集

• 特征分类

  • relevant feature：相关特征，对当前学习任务有用的属性、特征
    • 特征选择最重要的是确保不丢失重要特征
  • irrelevant feature：无关特征，对当前学习任务无用的属性、特征
  • redundant feature：冗余特征，包含的信息可以由其他特征中推演出来
    • 冗余特征通常不起作用，剔除可以减轻模型训练负担
    • 若冗余特征恰好对应完成学习任务所需要的中间概念，则是有益的，可以降低学习任务的难度

• 特征选择会降低模型预测能力，因为被剔除特征中可能包含有效信息

  • 保留尽可能多特征，模型性能会提升，模型更复杂、计算复杂度同样提升
  • 剔除尽可能多特征，模型性能会下降，模型更简单、降低计算复杂度

• 特征选择原因

  • 维数灾难问题：仅需要选择一部分特征构建模型，可以减轻 维数灾难问题，从此意义上特征选择和降维技术有相似动机
  • 剔除无关特征可以降低学习任务难度，简化模型、降低计算复杂度

• 特征选择方法可以分解为

  • 特征子集搜索
  • 特征子集评价：能判断划分之间差异的机制都能作为特征子集的准则

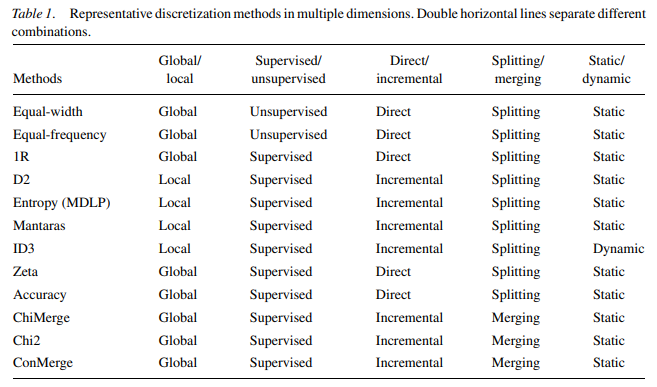
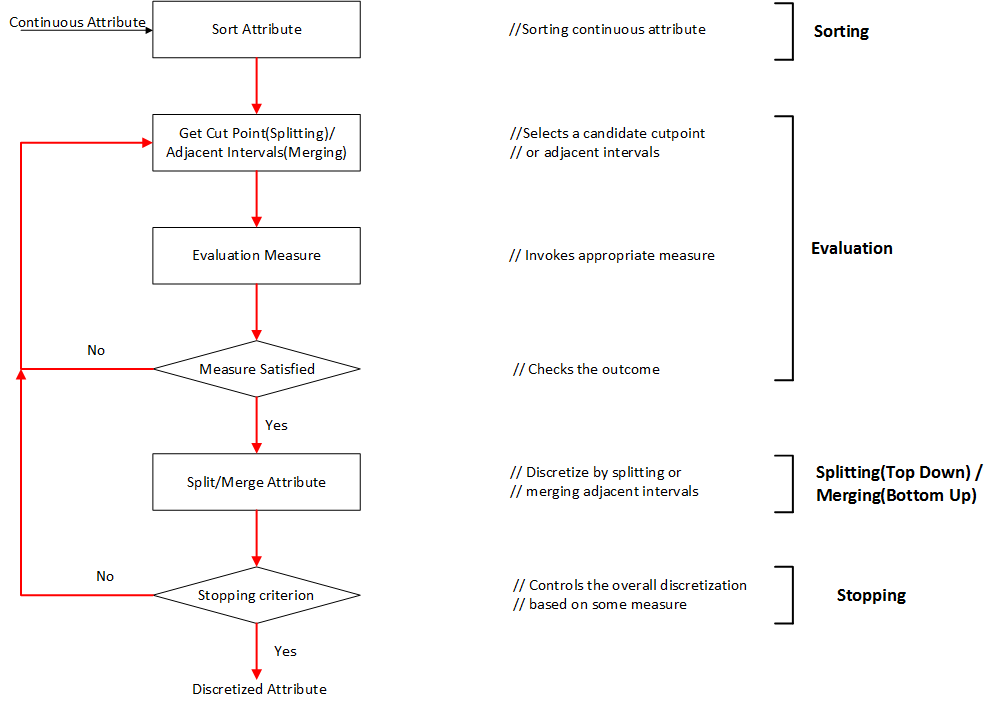
特征选择过程

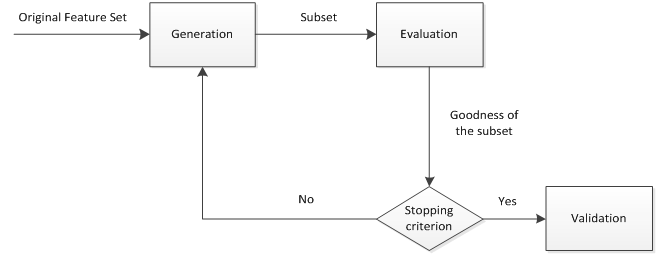
• generation procedure：产生过程，搜索特征子集
• evaluation function：评价函数，评价特征子集优劣
• stopping criterion：停止准则，与评价函数相关的阈值，评价函数达到与阈值后可以停止搜索
• validation procedure：验证过程，在验证数据集上验证选择特征子集的有效性

特征子集搜索

• 遍历：从初始特征集合选择包含所有重要信息的特征子集

  • 适合没有先验（问题相关领域）知识的情况
  • 特征数量稍多会出现组合爆炸

• 迭代：产生候选子集、评价优劣，基于评价结果产生下个候选子集

  • 不断迭代，直至无法找到更好的后续子集
  • 需要评价得子集数量较少
  • 可能无法找到最优子集

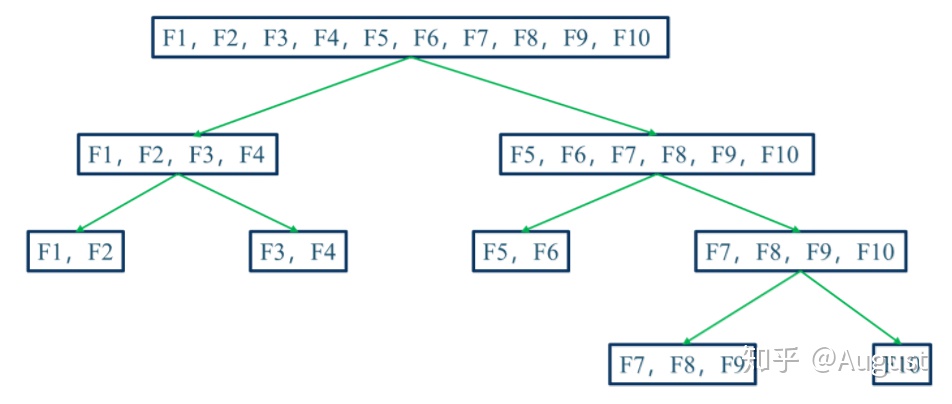
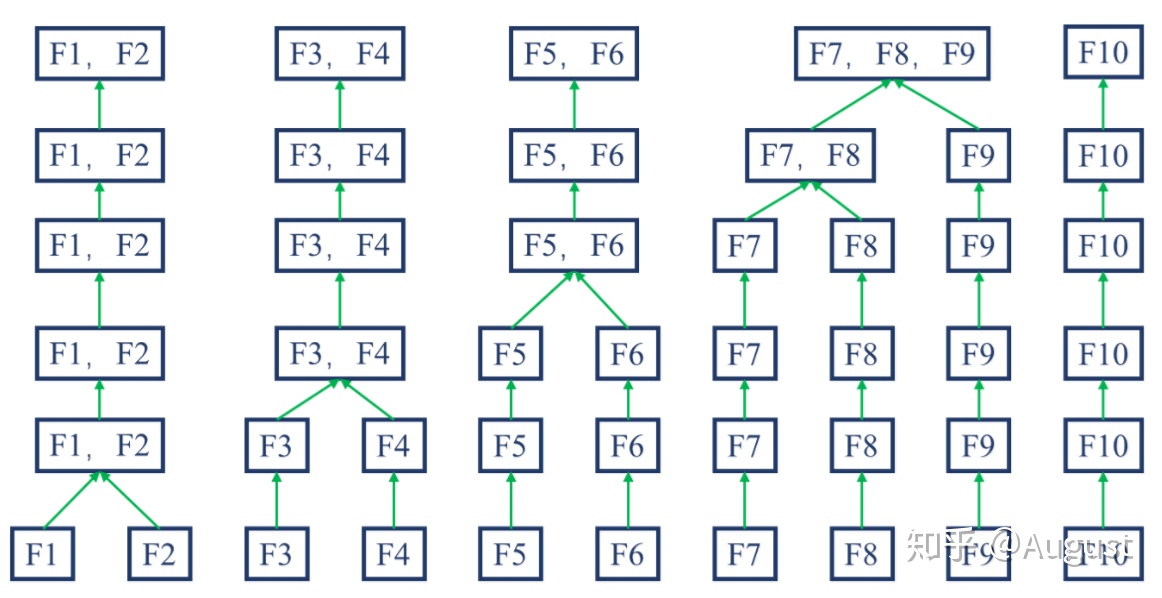
迭代搜索

• 给定特征 $A={A_1, A_2, \cdots, A_d}$，将每个特征视为候选子集（每个子集只有一个元素），对 $d$ 个候选子集进行评价

• 在上轮选定子集中加入特征，选择包含两个特征的最优候选子集

• 假定在 $k+1$ 轮时，最优特征子集不如上轮最优的特征子集，则停止生成候选子集，将上轮选定特征子集作为特征选择结果

• Forward Feature Elimination：前向特征选择，逐渐增加相关特征
• Backward Feature Elimination：后向特征选择，从完整特征集合开始，每次尝试去掉无关特征，逐渐剔除特征
• Bidirectional Feature Elimination：双向特征选择，结合前向、后向搜索

  • 每轮逐渐增加选定的相关特征，特征在后续迭代中确定不会被去除，同时减少无关特征

特征子集评价

特征子集评价：能判断划分之间差异的机制都能作为特征子集的选择准则

• 方差

  • 方差越大，特征对预测值区分能力越强

• 相关系数

  • Pearson 积矩相关系数
  • Kendell 秩相关系数
  • Spearman 秩相关系数
  • 卡方统计量

• 距离指标

• 划分增益

  • Gini 指数
  • IG 信息增益/互信息
  • 信息增益比

• 排序指标

  • AUC

特征问题定位

• 模型出现过拟合问题时，可能是特征工程步骤中出现信息泄露（数据穿越、标签入特征），一般通过单变量特征评价指标定位有问题的特征

• 数据泄露涉及的特征的定位（经验）
  • 线性模型
    • 单变量 AUC 值：超过 0.8 则高度可疑
  • 非线性模型（树）
    • 基于信息增益的特征重要性

Filter

过滤式：对数据集进行的特征选择过程与后续学习器无关，即设计统计量过滤特征，不考虑后续学习器问题

• 通过分析特征子集内部特点衡量特征优劣，描述自变量、目标变量的关联

• 特点

  • 时间效率高
  • 对过拟合问题较稳健
  • 倾向于选择单个、冗余特征，没有考虑特征之间相关性

单特征过滤

单特征过滤：直接选择合适特征子集评价标准处理各特征，选择满足要求特征

Relief: Relavant Features

Relief 方法：设置相关统计量度量特征重要性

• 特征子集对应统计量中每个分量对应一个初始特征，特征子集重要性由子集中每个特征对应的相关统计量分量之和决定

• 特征选择方法

  • 指定阈值 $k$：选择比 $k$ 大的相关统计量分量对应特征
  • 指定特征个数 $m$：选择相关统计量分量最大的 $m$ 个特征

• 只适合二分类问题，扩展变体 Relief-F 可以处理多分类问题

Wrapper

包裹式：把最终要使用的学习器性能作为特征子集评价标准，为给定学习器选择最有利其性能、特化的特征子集

• 优点
  • 直接针对特定学习器进行优化
  • 考虑了特征之间的关联性，通常训练效果较过滤式好
• 缺点
  • 特征选择过程中需要多次训练学习器，计算效率较低
  • 观测数据较少时容易过拟合

Las Vegas Wrapper

LVW：在 Las Vegas Method 框架下使用随机策略进行子集搜索，以最终分类器误差作为特征子集评价标准

• 包含停止条件控制参数T，避免每次子集评价训练特征子集开销过大
• 若初始特征数量很多、T设置较大、每轮训练时间较长，算法执行很长时间都不会停止
  • LVM 可能无法得到解（拉斯维加斯算法本身性质）

递归特征消除法

递归特征消除法：使用基模型进行多轮训练，每轮训练消除若干权值系数的特征，再基于特征集进行下一轮训练

Stepwise变量选择

• 前向变量选择
• 后向变量选择
• 前向-后向变量选择
• 最优子集选择

Embedded

嵌入式：将特征选择、学习器训练过程融合，在同一优化过程中同时完成，即学习器训练过程中自动进行特征选择

• 优点：兼具筛选器、封装器的优点
• 缺点：需要明确好的选择

正则化约束

$L_1$、$L_2$ 范数：主要用于线性回归、逻辑回归、SVM 等算法

• Ridge：$L_2$ 范数
• Lasso：$L_1$ 范数
  • 除降低过拟合风险，还容易获得稀疏解
  • 参数 $\lambda$ 越大，稀疏性越大，被选择特征越少
• SVM、逻辑回归
  • 超参参数范数权重越大，稀疏性越大，被选择特征越少

决策树

决策树思想：决策树自上而下选择分裂特征就是特征选择

• 所有树结点划分属性根据先后顺序组成的集合就是选择出来的特征子集

• 参见ml_models/unlinear_models/decision_tree

神经网络

神经网络：训练时同时处理贡献度问题，不重要特征权重被剔除

Feature Extraction/Feature Construction

特征提取/构建：把原始数据中转换为具有物理、统计学意义特征，构建新的人工特征

• 主观要求高

  • 对问题实际意义、相关领域有研究：思考问题形式、数据结构
  • 对数据敏感：需要观察原始数据
  • 分析能力强

• 目的：自动构建新特征

  • 信号表示：抽取后特征尽可能丢失较少信息
  • 信号分类：抽取后特征尽可能提高分类准确率

• 方法

  • 组合属性：混合属性创建新特征
  • 切分属性：分解、切分原有特征创建新特征，如将时间戳分割为日期、上下午

• 特征工程和复杂模型在某些方便不冲突

  • 虽然很多复炸模型能够学习复杂规律，类似自行构造特征
  • 但是考虑到计算资源、特征数量、学习效率，人工经验构造衍生特征是必要且有益的

• 特征选择：表示出每个特征对于模型构建的重要性
• 特征提取：有时能发现更有意义的特征属性
• 有时从额外划分特征构建，其相较于特征提取，需要人为的手工构建特征，偏经验、规则

通用特征提取

数值型

• 幅度调整：提高 SGD 收敛速度
  • 归一化
  • 标准化
• 数据变换
  • 数据标准化（参见 data_preprocessing）
  • 二阶、三阶变换
• 数据离散化：连续值分段
  • 等距切分：各类分布不均
  • 分位数切分：各类分布均匀，但异质性不均
• 平方、开根：增加非线性化

分类型

• one-hot 编码：赋予各特征等权
• hash 技巧：针对文本类别数据，统计文本词表、倾向
• 多分类转二分类：输入变量类别合并，超类
  • twoing 策略：使两个超类差异足够大的合并点（分割点）
  • ordering 策略：对有序类型，只有两个连续基类才能合并

统计型

• 统计特征
  • 跨记录聚集：特征取值在样本全体中的情况
    • 分位线
    • 比例
    • 次序
    • count（出现次数）
    • 均值
    • 方查
  • 记录内聚合：属于同记录的同类特征统计指标
    • 均值
    • 方查
• 时序特征
  • 视为连续型：持续时间、间隔时间
  • 视为离散值：一年中某些时间段

组合特征

• 特征拼接：GBDT 生成特征组合路径
• 特征冲突验证：匹配、等于、不等于
• 关联特征：图传播
  • 依赖于内部、外部关联图数据，如：
    • 账户作为节点：已能确认正、负例样本
    • 交易、社会关系作为边
    • 交易频次、金额作为权重
  • 图传播可以考虑多次传播，即考虑前一次的传播结果中置信度较高者作为下次的起始节点
• 特征交叉衍生：探索的范围较大，人工特征交叉衍生时建议最后考虑，根据经验：
  • 优先从单变量评价指标较好的特征开始
  • 连续特征内部可能会做交叉衍生
  • 但离散特征内部往往不做交叉衍生
    • one-hot 后特征对应维数较大
    • 单个维度信息量不多，交叉后维数爆炸，不适合某些模型，如：树模型
  • 从离散、连续特征中 分别选择 进行交叉
    • 交叉方式：连续特征为记录内聚合特征时，按离散特征分组聚合
    • 优先考虑此种交叉衍生

降维

Principal Component Analysis

PCA：主成分分析，找到数据中主成分，用主成分来表征原始数据，达到降维目的

• 思想：通过坐标轴转换，寻找数据分布的最优子空间
  • 特征向量可以理解为坐标转换中新坐标轴方向
  • 特征值表示对应特征向量方向上方差
    • 特征值越大、方差越大、信息量越大
    • 抛弃较小方差特征
• PCA缺陷：线性降维方法
  • KPCA：核主成分分析，核映射对PCA进行扩展
  • 流形映射降维方法：等距映射、局部线性嵌入、拉普拉斯 特征映射

步骤

• 对样本数据进行中心化处理（和统计中处理不同）
• 求样本协方差矩阵
• 对协方差矩阵进行特征值分解，将特征值从大至小排列
• 取前p个最大特征值对应特征向量作为新特征，实现降维

Linear Discriminant Analysis

LDA：线性判别分析，寻找投影方向，使得投影后样本尽可能按照 原始类别分开，即寻找可以最大化类间距离、最小化类内距离的方向

• 相较于PCA，LDA考虑数据的类别信息，不仅仅是降维，还希望 实现“分类”

• 优点：相较于PCA

  • LDA更适合处理带有类别信息的数据
  • 模型对噪声的稳健性更好

• 缺点

  • 对数据分布有很强假设：各类服从正太分布、协方差相等， 实际数据可能不满足
  • 模型简单，表达能力有限，但可以通过核函数扩展LDA处理 分布比较复杂的数据

• Fisher判别分析

Independent Component Analysis

ICA：独立成分分析，寻找线性变换$z=Wx$，使得$z$各特征分量 之间独立性最大

• 思想
  • 假设随机信号$x$服从模型 $$x = As$$

    • $s$：未知源信号，分量相互独立
    • $A$：未知混合矩阵

  • ICA通过观察$x$估计混合矩阵$A$、源信号$s$，认为源信号 携带更多信息

• 若原信号非高斯，则分解唯一，否则可能有无穷多分解
• 因子分析，也称Blind Source Separation（盲源分离）

算法

• 大多数ICA算法需要进行数据预处理：先用PCA得到主成分$Y$， 再把各个主成分各分量标准化得到$Z$满足

  • $Z$各分量不相关
  • $Z$各分量方差为1

• FastICA算法：寻找方向$w$使得随机变量$w^T z$某种 “非高斯性”度量最大化

  • 四阶矩

图像特征提取

• 提取边缘、尺度不变特征变换特征

• 以下是传统的图像特征提取方法，现在应该都是CNN进行特征 提取、分类
• 详情参见machine_learning/cv

LBP特征

• Sobel Operator
• Laplace Operator
• Canny Edge Detector

基于角点

• Moravec
• Harris
• GoodFeaturesToTrack
• FAST

基于尺度空间

• Scale-Invariant Feature Transform
• Speeded Up Robust Feature
• Brief
• Oriented Brief

HOG特征

方向梯度直方图特征：通过计算、统计图像局部区域梯度方向直方图 实现特征描述

步骤

• 归一化处理：图像转换为灰度图像，再利用伽马校正实现
  • 提高图像特征描述对光照、环境变量稳健性
  • 降低图像局部阴影、局部曝光、纹理失真
  • 尽可能抵制噪声干扰
• 计算图像梯度
• 统计梯度方向
• 特征向量归一化（块内）
  • 克服光照不均匀变化及前景、背景对比差异
• 生成特征向量

文本特征提取

• 具体参见ml_specification/natural_language_processing/#todo

词袋模型

词袋模型：将文本以词为单位切分token化

• 文章可以表示为稀疏长向量，向量每个维度代表一个单词

  • 针对有序语句，将单词两两相连
  • 维度权重反映单词在原文章中重要程度
    • 通常使用TF-IDF统计量表示词权重

• TF-IDF

  $$\begin{align*} TF-IDF(t, d) & = TF(t, d) * IDF(t) \\ IDF(t) & = log \frac {文章总数} {包含单词t的文章总数 + 1} \end{align*}$$

  • $TF(t, d)$：单词$t$在文档$d$中出现的频率
  • $IDF(t)$：逆文档频率，衡量单词对表达语义的重要性

    • 若单词在多篇文章中出现过，则可能是通用词汇，对区分 文章贡献较小，$IDF(t)$较小、权重较小

N-gram模型

N-gram模型：将连续出现的$n, n \leq N$个词组成的词组N-gram 作为单独特征放到向量中

• 相较于词袋模型，考虑单词组合意义
• word stemming：将不同词性单词统一为同一词干形式
  • 同一个词可能有多种词性变化，却拥有相同含义

Word-Embedding模型

词嵌入模型：将每个词都映射为低维空间上的稠密向量

• Word2Vec：常用词嵌入模型，底层神经网络

  • Continuous Bag of Words：根据上下文词语预测当前词 生成概率
  • Skip-gram：根据当前词预测上下文中各个词的生成概率

• 实际上直接使用矩阵作为源文本特征作为输入进行训练，难以 得到好结果，往往需要提取、构造更高层特征

参数初始化

• 合适参数初始化可以加速模型训练

  • 避免反向传播的梯度信息被放大、缩小
  • 导致出现梯度爆炸、消失

• 参数初始化值满足如下条件，则训练过程中能较好防止梯度信号被放缩

  $$\begin{align*} E(a^{(l-1)}) & = E(a^{(l)}) \\ Var(a^{(l-1)}) & = Var(a^{(l)}) \end{align*}$$
  • 激活值均值为 0
  • 每层激活值方差保持一致

常数（零值）初始化

常数初始化：将所有权值初始化为常数

• 任意常数初始化方法性能都不好，甚至无法训练

  • 反向传播算法更新参数时，各参数各维度导数一致、更新后权值一致
  • 各神经元在演化过程中对称，无法学习不同特征，退化为单神经元

• 在激活函数选择线性激活函数时

  • 过大的初始化权重可能导致梯度爆炸
  • 过小的初始化值可能导致梯度消失

随机初始化

随机初始化：随机生成参数

• 权重 $W$：均值 0、方差 1 的正态分布生成，并乘以较小常数（如：0.01）

  • 权值被初始化不同值，解决零值初始化存在网络退化问题
  • 但较小权值可能导致梯度弥散，无法学习

• 偏置 $b$：初始化为 0

  • 帮助变换系统初始处于线性域，加快梯度传播

Xavier 初始化

Xavier 初始化：适合 tanh 激活函数的参数初始化方式

$$Var(W^{(l)}) = \frac 2 {n^{(l-1)} + n^{(l)}}$$

• $n^{(l)}$：第 $l$ 层神经元数量

He 初始化

He 初始化：适合 ReLU 激活函数的参数初始化方式

$$Var(W^{(l)}) = \frac 1 {n^{(l)}}$$

• 基于 Xavier 初始化在 ReLU 上的改进，实际中二者都可以使用

超参搜索

Random Search

Grid Search

Bayesian Optimization

数据抽样

• 抽样作用

  • 提高速度、效率，将精力放在建立模型、选择模型上
  • 帮助分析特殊性问题：有些问题涉及到破坏性试验，抽取产品的一部分做耐用性实验经济有效
  • 降低成本：合理抽样可以保证在大部分信息不丢失情况下，降低数据采集、社会调查成本

• 从效率、成本角度看，适当、合理抽样有必要

  • 数据越多信息越丰富、数据量尽量多为好
  • 抽样可以降低求解的时空代价，但是可能会丢失部分信息，可能会使分析结果产生偏差
  • 在分析阶段，若抽样误差能够接受，完全可以抽样

• 样本应能充分代表总体

  • 一般样本容量越大，和总体的相似程度越高，样本质量越高
  • 但大样本不等于总体：理论上再大的局部抽样也不如随机抽样有代表性

样本评价

• 样本容量、样本质量是衡量抽样样本的两个最重要因素
  • 样本容量：抽样过程中抽取的样本数
  • 样本质量：衡量抽样样本的代表性

样本质量

样本质量：抽样样本与整体的相似性

$$\begin{align*} J(S, D) & = \frac {1} {D} \sum_{k=1}^{r} J_{k}(S, D) \\ J_{k}(S, D) & = \sum_{j=1}^{N_k}(P_{Sj} - P_{Dj}) log \frac {P_{Sj}} {P_{Dj}} \\ Q(s) & = exp(-J) \end{align*}$$

• $D$：数据集，包含 $r$ 个属性
• $S$：抽样样本集
• $J_k=J(S, D)$：Kullblack-Laible 散度，数据集 $S$、$D$ 在属性 $k$ 上偏差程度，越小偏差越小
• $Q(S) \in [0, 1]$：抽样集 $S$ 在数据集 $D$ 中的质量，越大样本集质量越高

• 若整体 $D$ 分布稀疏，容易得到 $S$ 在某些数据点观测值数为 0，得到 $I(S, D) \rightarrow infty$

  • 可以把该点和附近的点频率进行合并，同时调整总体频率分布
  • 过度合并会导致无法有效衡量数据集局部差异性

• 对于连续型变量

  • 可以把变量进行适当分组：粗糙，不利于刻画数据集直接的局部差异
  • 计算数据集各个取值点的非参估计，如核估计、最近邻估计等，再在公式中用各自的非参估计代替相应频率，计算样本质量

• 数据包含多个指标时

  • 可以用多个指标的平均样本质量衡量整体样本质量
  • 也可以根据指标重要程度，设置不同的权重

样本容量

• 样本容量是评价样本的另一个重要维度
  • 样本量大、质量好、准确性高，但计算效率低
  • 样本质量差、准确性低、计算效率高
  • 样本质量提高不是线性的，高位样本容量上，边际效用往往较低
  • 同一样本容量的不同样本的样本质量也会有差异，即样本质量不是样本容量的单调函数，包含随机扰动

Statistical Optimal Sample Size

SOSS：统计最优样本数

• 输入：数据集 $D$，包含 $N$ 个实例

• 根据某种抽样方法，随机产生 $R$ 个样本容量分别为 $n_i, n_i \in [1, N]$ 的样本 $S$

  • $n_i$ 取值较小处应密度比较大，因为随着 $n_i$ 增加，样本质量趋近 1，不需要太多样本
  • 可以考虑使用指数序列产生在较大值处稀疏的序列作为 $n_i$ 序列的取值

• 计算每个样本 $S$ 在数据集 $D$ 中的样本质量 $Q$

  • 并计算各个样本容量对应的样本质量均值 $\bar {Q_{n}}$
  • 绘制曲线 $(n, \bar {Q_{n}})$

• 根据给定的样本质量要求，在样本容量对应样本质量的曲线上确定近似的最优样本容量

测试集、训练集

• 测试集、训练集划分逻辑前提

  • 在样本量足够的情况下，减少部分样本量不会影响模型精度
  • 模型评价需要使用未参与建模数据验证，否则可能夸大模型效果

• 测试集、训练集划分作用

  • 测试集直接参与建模，其包含信息体现在模型中
  • 训练集仅仅用于评价模型效果，其包含信息未被利用，
  • 因此，若无评价、对比模型需求，或有其他无需划分测试集即可评价模型，则划分测试集无意义

测试集、训练集划分

Hold Out

旁置法：将样本集随机划分为训练集、测试集，只利用训练集训练 模型

• 适合样本量较大的场合
  • 减少部分训练数据对模型精度影响小
  • 否则大量样本未参与建模，影响模型精度
• 常用划分比例
  • 8:2
  • 7:3
• 旁置法建立模型可直接作为最终输出模型
  • 旁置法一般只建立一个模型
  • 且使用旁置法场合，模型应该和全量数据训练模型效果差别不大

N-fold Cross Validation

N 折交叉验证：将数据分成N份，每次将其中一份作为测试样本集， 其余N-1份作为训练样本集

• N折交叉验证可以视为旁置法、留一法的折中

  • 克服了旁置法中测试样本选取随机性的问题：每个样本都 能作为测试样本
  • 解决了留一法计算成本高的问题：重复次数少

• 典型的“袋外验证”

  • 袋内数据（训练样本）、袋外数据（测试样本）分开

• N折交叉验证会训练、得到N个模型，不能直接输出

  • 最终应该输出全量数据训练的模型
  • N折建立N次模型仅是为了合理的评价模型效果，以 N 个模型的评价指标（均值）作为全量模型的评价

Leave-One-Out Cross Validation

留一法：每次选择一个样本作为测试样本集，剩余 n-1 个观测值作为训练样本集，重复 n 次计算模型误差

• 可以看作是 N 折交叉验证的特例

数据泄露

• 特征泄露：训练过程中使用有包含有上线之后无法获取的数据

  • 时序数据中数据穿越：使用未来数据训练模型，模型将学习不应获取的未来信息

• 记录泄露/训练数据泄露：切分数据集时训练集包含了测试集中部分数据

  • 会导致评估指标失真

样本重抽样

Bootstrap

重抽样自举：有放回的重复抽样，以模拟多组独立样本

• 对样本量为 $n$ 的样本集 $S$
• 做$k$次有放回的重复抽样
  • 每轮次抽取 $n$ 个样本
  • 抽取得到样本仍然放回样本集中
• 得到 $k$ 个样本容量仍然为 $n$ 的随机样本 $S_i，(i=1,2,…,k)$

过采样

• over-sampling：过采样，小类数据样本增加样本数量

• synthetic minority over-sampling technique：过采样算法，构造不同于已有样本小类样本
  • 基于距离度量选择小类别下相似样本
  • 选择其中一个样本、随机选择一定数据量邻居样本
  • 对选择样本某属性增加噪声，构造新数据

SMOTE

Borderline-SMOTE

欠采样

• under-sampling：欠采样，大类数据样本减少样本数量

数值化：分类->数值

Ordinal Encoding

序号编码：使用一位序号编码类别

• 一般用于处理类别间具有大小关系的数据
  • 编码后依然保留了大小关系

One-hot Encoding

独热编码：采用N位状态位对N个可能取值进行编码

• 一般用于处理类别间不具有大小关系的特征

• 独热编码后特征表达能力变差，特征的预测能力被人为拆分为多份

  • 通常只有部分维度是对分类、预测有帮助，需要借助特征选择降低维度

• 在经典统计中，为避免完全多重共线性，状态位/哑变量会比取值数量少 1

优点

• 能处理非数值属性
• 一定程度上扩充了特征
• 编码后向量时稀疏向量：可以使用向量的稀疏存储节省空间
• 能够处理缺失值：高维映射方法中增加维度表示缺失

缺点

• k-NN 算法：高维空间两点间距离难以有效衡量

• 逻辑回归模型：参数数量随维度增加而增大，增加模型复杂度，容易出现过拟合

• 决策树模型

  • 产生样本切分不平衡问题，切分增益非常小
    • 每个特征只有少量样本是 1，大量样本是 0
    • 较小的拆分样本集占总体比例太小，增益乘以所占比例之后几乎可以忽略
    • 较大拆分样本集的几乎就是原始样本集，增益几乎为 0
  • 影响决策树的学习
    • 决策树依赖数据统计信息，独热编码将数据切分到零散小空间上，统计信息不准确、学习效果差
    • 独热编码后特征表达能力边人为拆分，与其他特征竞争最优划分点失败，最终特征重要性会比实际值低

Binary Encoding

二进制编码：先用序号编码给每个类别赋予类别 ID，然后将类别 ID 对应二进制编码作为结果

• 本质上利用二进制类别 ID 进行哈希映射，得到 0/1 特征向量
• 特征维度小于独热编码，更节省存储空间

Weight of Evidence Encoding

WOE 编码：以分类变量各取值的 WOE 值作为编码值

$$\begin{align*} WOE_i & = log(\frac {\%B_i} {\%G_i}) \\ & = log(\frac {\#B_i / \#B_T} {\#G_i / \#G_T}) \end{align*}$$

• $\%B_i, \%G_i$：分类变量取第 $i$ 值时，预测变量为 B 类、G 类占所有 B 类、G 类比例
• $#B_i, #B_T$：分类变量取第 $i$ 值时，预测变量为 B 类占所有 B 类样本比例
• $#G_i, #G_T$：分类变量取第 $i$ 值时，预测变量为 G 类占所有 G 类样本比例

• WOE 编码是有监督的编码方式，可以衡量分类变量各取值中

  • B 类占所有 B 类样本比例、G 类占所有 G 类样本比例的差异
  • B 类、G 类比例，与所有样本中 B 类、G 类比例的差异

• WOE 编码值能体现分类变量取值的预测能力，变量各取值 WOE 值方差越大，变量预测能力越强

  • WOE 越大，表明该取值对应的取 B 类可能性越大
  • WOE 越小，表明该取值对应的取 G 类可能性越大
  • WOE 接近 0，表明该取值预测能力弱，对应取 B 类、G 类可能性相近

优势

• 相较于 one-hot 编码

  • 特征数量不会增加，同时避免特征过于稀疏、维度灾难
  • 避免特征筛选过程中，一部分特征取值被筛选，一部分被遗弃，造成特征不完整
  • 将特征规范到同一尺度的数值变量，同时也便于分析特征间相关性

• 在 LR 模型中，WOE 编码线性化赋予模型良好的解释性

  • WOE 编码本身即可反应特征各取值贡献
  • 可以用于给评分卡模型中各分箱评分

分类化/离散化：数值->分类

• 分类型变量本质上无法建模，因为取值从含义上无法进行数值计算
• 将数值型映射为分类型，往往只是中间步骤，最终会将分类型取值映射回数值型

• 若分箱数量为 2，也被成为是二元化/布尔化

离散化综述

• 模型使用离散特征、连续特征，是“海量离散特征+简单模型”、“少量连续特征+复杂模型”的权衡

  • 海量离散特征+简单模型：难点在于特征工程，成功经验可以推广，可以多人并行研究
  • 少量连续特征+复杂模型：难点在于模型调优，不需要复杂的特征工程

• 一般的，连续特征对预测结果影响不会突变，合理的离散化不应造成大量信息丢失

  • 且若特征存在突变，模型将难以拟合（线性模型尤其）
  • 反而更应该离散化为多个分类特征，方便引入非线性

• 事实上，根据Cover定理，离散化增加特征维度类似于投影至高维，更可能得到较优模型（也更容易过拟合）

  • 极限角度，对所有特征、取值均离散化，则可以得到完全可分模型（除特征完全一样分类不同）

描述角度

• supervised vs. unsupervised：是否使用分类信息指导离散化过程

  • 无监督
    • 如：等距、等频划分
    • 无法较好的处理异常值、不均匀分布
  • 有监督
    • 利用分类信息寻找合适切分点、间隔
    • 根据使用分类信息的方式有许多种

• dynamic vs. static：离散化、分类是否同时进行

• global vs. local：在特征空间的局部还是全局进行离散化

• spliting vs. merging/top-down vs. bottom-up：自顶向下划分还是自底向上合并

• direct vs. incremental：直接根据超参数确定分箱数量还是逐步改善直到中止准则

典型过程

• sort：排序
• evaluate：评估分割点
• split or merge：划分、合并
• stop：停止离散化

评价

• Simplicity：可用切分点数量衡量简单性
• Consistency：可以通过最小不一致数量衡量一致性
  • 不一致：样本具有相同的特征取值，但分类不同
  • 分箱最小不一致数量则为，箱内样本数量减最大类别数量
• Accuracy：可通过分类器进行交叉验证的准确率衡量

优势

• 方便工业应用、实现

  • 离散特征的增加、减少容易，方便模型迭代
  • 特征离散化处理缺失值、异常值更方便，可直接将其映射为某取值
  • 数值化后可指定取值类型，如：one-hot编码为为稀疏向量
    • 內积速度快
    • 存储方便
    • 容易扩展

• 方便引入历史经验

  • 可以自由调整离散化结果，结合机器学习和历史经验得到最终的离散化结果

• 模型更稳健

  • 模型不再拟合特征具体值，而是拟合某个概念，能够对抗数据扰动，更稳健
  • 对异常数据鲁棒性更好，降低模型过拟合风险
  • 某些场合需要拟合参数值更少，降低模型复杂度

• （引入）非线性提升模型表达能力

  • 利用经验、其他信息将数值特征分段，相当于引入非线性，提升线性模型表达能力
  • 方便引入交叉特征，提升模型表达能力

适合场景

• 离散化特征更适合 LR 等线性模型

  • 如下离散化优势：方便引入非线性等
  • 模型中所有特征都会被考虑，考虑细节、个体（包括 $L_1$ 范数也是被考虑后剔除）

• GBDT 等树、抽样模型则不适合

  • 特征离散化后，由于抽样误差的存在，可能存在某些离散特征对样本预测能力非常强，非线性模型容易给这些特征更大权重，造成过拟合
    • 如：刚好抽取的 1000 个样本中某离散特征取值为 1 者全为正样本
  • 树模型每次使用一个特征划分节点，特征数量较多不利于模型训练
    • 若单个离散化特征预测能力不强，由于树深度限制，只有少量特征被作为划分依据，模型可能不收敛、表达能力更差
    • 若单个离散化特征预测能力强，连续特征也应该也有较好效果

无监督

• 无监督分箱仅仅考虑特征自身数据结构，没有考虑特征与目标之间的关系

等频/等距/经验分箱

• 分箱逻辑

  • 等频分箱：排序后按数量等分
    • 避免离散化后特征仍然为长尾分布、大量特征集中在少量组内
    • 对数据区分能力弱
  • 等距分箱：取值范围等分
  • 经验分箱

• 分箱数量、边界超参需要人工指定

  • 根据业务领域经验指定
  • 根据模型指定：根据具体任务训练分箱之后的数据集，通过超参数搜索确定最优分桶数量、边界

• 分箱经验、准则

  • 若组距过大，组内属性取值差距过大
    • 逻辑上分类不能够代表组内全部样本，组内取值影响可能完全不同
  • 若组距过小，组内样本过少
    • 随机性太强，不具备统计意义上说服力
    • 特征影响跳变过多

聚类分箱

• K-Means 聚类
• 层次聚类

• 聚类过程中需要保证分箱有序

有监督

Binning：1R 分箱

• 分箱逻辑、步骤
  • 将样本排序，从当前位置开始
    • 初始化：以允许的最少样本作为一箱，将箱内最多类别作为箱标签
    • 扩展：若下个样本类别与箱标签相同，则划至箱内
  • 重复以上，得到多个分箱
  • 将相邻具有相同标签的箱合并，得到最终分箱结果

Splitting

• 基于信息熵的 split，具体划分依据如下
  • ID3：信息增益
  • C4.5：信息增益比
  • D2：
  • Minimum Description Length Principle：描述长度

Merge分箱

• 基于依赖相关的 merge，具体划分依据如下
  • Chimerge：使用卡方值衡量两个相邻区间是否具有类似分布，若具有类似分布则将其合并

具体算法

• 输入：目标分箱数量 $N$
• 初始化
  • 将变量升序排列
  • 为减少计算量，若初始分箱数量大于阈值 $N_{max}$，则利用等频分箱进行粗分箱
  • 缺失值单独作为一个分箱
• 合并区间
  • 计算每对相邻区间的卡方值
  • 将卡方值最小区间合并
  • 重复以上直至分箱数量不大于 $N$
• 分箱后处理
  • 合并纯度为 1（只含有某类样本）的分箱
  • 删除某类样本占比超过 95% 的分箱
  • 若缺失值分箱各类样本占比同非缺失值分箱，则合并

Internal Covariate Shift

ICS：由于网络参数变化，引起内部节点（输入）数据分布发生变化的过程

• 网络中层与层之间高度耦合，具有强关联性

  • 网络中任意层都可以视为单独网络
  • 上层输入可视为作为当前层外部输入

• 随训练进行，网络中参数不断发生改变

  • 任意层中参数变化会导致之后层输入发生改变
  • 高层需要不断适应输入分布的改变，即其输入分布性质影响 该层训练
  • 由此导致模型训练困难

负面影响

• 上层网络需要不断调整输入适应数据分布变换，降低网络学习 效率

• 输入数据量级不稳定、各维度数据量级差距不稳定

  • 降低学习效率
    • 小量级维度参数要求更小的学习率
    • 否则参数可能在最优解附近反复波动
  • 容易出现梯度消失，难以训练饱和非线性模型
    • 大量级维度训练过程中容易陷入梯度饱和区，参数更新 速度慢，减缓网络收敛速度
    • 训练过程中参数更新更有可能使得输入移向激活函数 饱和区
    • 且该效应随着网络深度加深被进一步放大
  • 参数初始化需要更复杂考虑

• 还可以使用非饱和激活函数ReLU等避免陷入梯度饱和区

Batch Normalization

Batch Normalization：规范化batch数据，使样本各维度 标准化，即均值为0、方差为1

$$\begin{align*} \y & = BN_{\gamma, \beta}(z) = \gamma \odot \hat z + \beta \\ \hat z & = \frac {z - E(z)} {\sqrt {Var(z) + \epsilon}} \end{align*}$$

• $B$：mini-batch
• $z, y$：某层输入向量、规范化后输入向量 （即以个神经元中激活前标量值$z=Wx+b$为一维）
• $\odot$：逐元素乘积
• $E(x)$：均值使用移动平均均值
• $Var(x)$：方差使用移动平均无偏估计
• $\gamma, \beta$：待学习向量，用于恢复网络的表示能力
• $\epsilon$：为数值计算稳定性添加

• BN可以视为whitening的简化

  • 简化计算过程：避免过高的运算代价、时间
  • 保留数据信息：未改变网络每层各特征之间相关性

• BN层引入可学习参数$\gamma, \beta$以恢复数据表达能力

  • Normalization操作缓解了ICS问题，使得每层输入稳定 ，也导致数据表达能力的缺失
  • 输入分布均值为0、方差为1时，经过sigmoid、tanh激活 函数时，容易陷入其线性区域
  • $\gamma = \sqrt {Var(z)}, \beta = E(z)$时为等价变换 ，并保留原始输入特征分布信息

• Whitening：白化，对输入数据变换使得各特征同均值、 同方向、不相关，可以分为PCA白化、ZCA白化

训练

• 规范化在每个神经元内部非线性激活前$z=Wu$进行，而不是 [也]在上一层输出$u$上进行，即包含BN最终为

  $$z = act(BN(Wu))$$

  • $act$：激活函数
  • 偏置$b$：可以被省略，BN中减去均值

  • $u$的分布形状可以在训练过程中改变
  • 而$u$两次正则化无必要
  • $z=Wu$分布更可能对称、稠密、类似高斯分布

• 以batch统计量作为整体训练样本均值、方差估计

  • 每层均需存储均值、方差的移动平均统计量用于测试时 归一化测试数据

• 对卷积操作，考虑卷积特性，不是只为激活函数（即卷积核） 学习$\gamma, \beta$，而是为每个feature map学习 （即每个卷积核、对每个特征图层分别学习）

预测

• 预测过程中各参数（包括均值、方差）为定值，BN仅仅对数据 做了线性变换

  • 使用训练总体的无偏统计量对测试数据归一化 （训练时存储）

    $$\begin{align*} \mu_{test} & = E(\mu_{batch}) \\ \sigma^2_{test} = \frac m {m-1} E(\sigma^2_{batch}) \end{align*}$$

  • 还可以使用样本指数加权平均统计量

用途

• BN通过规范化输入数据各维度分布减少ICS，使得网络中每层 输入数据分布相对稳定

• 实现网络层与层之间的解耦

  • 方便迁移学习
  • 加速模型学习速度：后层网络无需不断适应输入分布变化， 利于提高神经网络学习速度

• 降低模型对网络超参数、初始值敏感度，使得网络学习更加稳定

  • 简化调参过程
  • 允许使用更大的学习率提高学习效率
  $$\begin{align*} BN(Wu) & = BN((aW)u) \\ \frac {\partial BN(aWu)} {\partial u} & = \frac {\partial BN(Wu)} {\partial u} \\ \frac {BN(aWu)} {\partial aW} & = \frac 1 a \frac {\partial BN(Wu)} {\partial W} \end{align*}$$

  • $a$：假设某层权重参数变动$a$倍

  • 激活函数函数输入不受权重$W$放缩影响
  • 梯度反向传播更稳定，权重$W$的Jacobian矩阵将包含接近 1的奇异值，保持梯度稳定反向传播

• 允许网络使用饱和激活函数（sigmoid、tanh等），而不至于 停滞在饱和处，缓解梯度消失问题

  • 深度网络的复杂性容易使得网络变化积累到上层网络中， 导致模型容易进入激活函数梯度饱和区

• 有正则化作用，提高模型泛化性能，减少对Dropout的需求

  • 不同batch均值、方差有所不同，为网络学习过程增加随机 噪声
  • 与Dropout关闭神经元给网络带来噪声类似，一定程度上 有正则化效果

Layer Normalization

层归一化：假设非线性激活前的输入随机变量分布接近，可以直接 基于每层所有非线性激活前输入估计均值、方差

$$\begin{align*} \mu^l & = \frac 1 H \sum_{i=1}^H h_i^l \\ \sigma^l &= \sqrt {\frac 1 H \sum_{i=1}^H (h_i^l - \mu^l)^2} \\ h^l & = W^l x^{l-1} + b^l \\ LN(h^l) & = \frac {g^l} {\sigma^l} \odot (h^l - \mu^l) + b^l \\ x^l & = g(LN(h^l)) \end{align*}$$

• $h^l$：第$l$隐层激活前值
• $\mu^l, \sigma^l$：第$l$隐层对应LN均值、方差 （标量，是同层神经元激活前值统计量）

• 相对于BN，其适应范围更广

  • 循环神经网络中，BN无法处理长于训练序列的测试序列
  • BN无法应用到在线学习、超大分布式模型任务，此时训练 batch较小，计算的均值、方差无法有效代表训练总体

• LN假设非线性激活前输入随机变量分布接近，而CNN网络中图像 边缘对应kernel大量隐藏单元未被激活，假设不成立，所以 CNN网络中LN效果没有BN效果好

指数类

Sigmoid

将实数映射到(0, 1)区间

$$sigmoid(z) = \frac 1 {1+e^{-z}}$$

• $z= wx+b$

• 用途

  • 隐层神经元输出
  • 二分类输出

• 缺点

  • 激活函数计算量大，BP算法求误差梯度时，求导涉及除法
  • 误差反向传播时容易出现梯度消失
  • 函数收敛缓慢

Hard_Sigmoid

计算速度比sigmoid激活函数快

$$hard_signmoid(z) = \left \{ \begin {array} {l} 0 & z < -2.5 \\ 1 & z > 2.5 \\ 0.2*z + 0.5 & -2.5 \leq z \leq 2.5 \\ \end {array} \right.$$

• $z= wx+b$

Softmax

主要用于多分类神经网络输出

$$softmax(z_i) = \frac {e^{z_i}} {\sum_{k=1}^K e^{z_k}}$$

• $z_i = w_i x + b_i$：$(w_i, b_i)$组数同分类数量，和输入 $x$维度无关

• $K$：分类数目

• 工程意义：指数底

  • 可导$max$：拉开数值之间差距
  • 特征对输出结果为乘性：即$z_i$中输入增加会导致输出 随对应权重倍数增加
  • 联合交叉熵损失避免导数溢出，提高数值稳定性

• 理论意义：概率论、最优化

  • softmax符合最大熵原理
  • 假设各标签取值符合多元伯努利分布，而softmax是其 link functiond的反函数#todo
  • 光滑间隔最大函数

• Softmax回归参数$(w_i, b_i$$冗余，可以消去一组

Softplus

$$softplus(z) = log(exp(z)+1)$$

• $z = wx + b$

Tanh

双曲正切函数

$$\begin{align*} tanh(z) & = \frac {sinhz} {coshz} \\ & = \frac {e^z - e^{-z}} {e^z + e^{-z}} \\ \end{align*}$$

• $z = wx + b$
• $\frac{\partial tanh(z)}{\partial z} = (1 - tanh(z))^2$ ：非常类似普通正切函数，可以简化梯度计算

线性类

Softsign

$$softsign(z) = \frac z {abs(z) + 1)}$$

ReLU

Rectfied Linear Units：修正线性单元

$$relu(z, max) = \left \{ \begin{array} {l} 0 & z \leq 0 \\ z & 0 < x < max \\ max & z \geq max \\ \end {array} \right.$$

LeakyReLU

Leaky ReLU：带泄露的修正线性

$$relu(z, \alpha, max) = \left \{ \begin {array} {l} \alpha z & z \leq 0 \\ z & 0 < z < max \\ max & z \geq max \\ \end {array} \right.$$

• $\alpha$：超参，建议取0.01

• 解决了$z < 0$时进入死区问题，同时保留了ReLU的非线性特性

Parametric ReLU

PReLU：参数化的修正线性

$$prelu(z) = \left \{ \begin{array} {l} \alpha z & z < 0 \\ z & z> 0 \\ \end{array} \right.$$

• $\alpha$：自学习参数（向量），初始值常设置为0.25，通过 momentum方法更新

ThreshholdReLU

带阈值的修正线性

$$threshhold_relu(z, theta)= \left \{ \begin{array} {l} z & z > theta \\ 0 & otherwise \\ \end{array} \right.$$

Linear

线性激活函数：不做任何改变

线性指数类

Exponential Linear Unit

Elu：线性指数

$$elu(z, \alpha) = \left \{ \begin{array} {l} z & z > 0 \\ \alpha (e^z - 1) & x \leqslant 0 \\ \end{array} \right.$$

• $\alpha$：超参

• $x \leq 0$时，$f(x)$随$x$变小而饱和
  • ELU对输入中存在的特性进行了表示，对缺失特性未作定量 表示

• 网络深度超超过5层时，ELU相较ReLU、LReLU学习速度更快、 泛化能力更好

Gausssion Error Liear Unit

GELU：ReLU的可导版本

Selu

可伸缩指数线性激活：可以两个连续层之间保留输入均值、方差

• 正确初始化权重：lecun_normal初始化
• 输入数量足够大：AlphaDropout
• 选择合适的$\alpha, scale$值

$$selu(z) = scale * elu(z, \alpha)$$

梯度消失

激活函数导数太小（$<1$），压缩误差（梯度）变化

Dropout

Dropout：训练时根据随机隐藏部分神经元、对应连接边避免 过拟合

固定概率丢弃

Dropout最简单方法：设置固定概率p，对每个神经元以概率p判定 是否需要保留

$$\begin{align*} y & = f(W * d(x) + b) \\ d(x) & = \left \{ \begin{array}{l} m \odot x, & 训练阶段 px, & 测试阶段 \end{array} \right. \end{align*}$$

• $d(x)$：丢弃函数
• $m \in {0, 1}^d$：丢弃掩码，通过概率为p的伯努利 分布随机生成

• $p$可以设置为0.5，对大部分网络、任务比较有效

  • 此时随机生成多的网络最具多样性

• 训练时

  • 激活神经元数量为原来的p倍
  • 每个batch分别进行drop，相当于对每个batch都有独特网络

• 测试时

  • 所有神经元都被激活，造成训练、测试时网络输出不一致， 需将每个神经元输出乘p避免
  • 也相当于把不同网络做平均

• 在预测时，类似bagging技术将多个模型组合

  • 只是类似，各个drop后的子网并不独立，在不同子网中相同 神经元的权重相同
  • 多个模型组合组合可以一定程度上抵消过拟合
  • 因为在训练时子网中部分神经元被drop，剩余部分权重相较 完全网络有$\frac 1 {1-p}$，所以在完整网络中，各部分 权重需要$ * (1-p)$

• 讲道理应该是隐藏部分神经元而不是连接，否则会使神经元偏向 某些输入，还不如隐藏部分神经元，这样可以让神经元随机降低 样本权重，理论上能减弱过拟合

丢弃方法

• 输入层神经元丢弃率更接近1，使得输入变化不会太大

  • 输入层神经元丢失时，相当于给数据增加噪声，提高网络 稳健性

• 循环神经网络丢弃

  • 不能直接丢弃隐状态，会损害循环网络在时间维度上的记忆 能力
  • 简单方法：可以考虑对非循环连接进行随机丢弃
  • 变分丢弃法：根据贝叶斯对丢弃法是对参数的采样解释， 采样参数需要每个时刻保持不变
    • 需要对参数矩阵的每个元素随机丢弃
    • 所有时刻使用相同的丢弃掩码

解释

• 集成学习解释

  • 每次丢弃，相当于从原网络采样得到子网络
  • 每次迭代，相当于训练不同的子网络，共享原始网络参数
  • 最终网络可以近似看作是集成了指数个不同网络的组合模型

• 贝叶斯学习解释

  • 对需要学习的网络$y = f(x, \theta)$，贝叶斯学习假设 参数$\theta$为随机向量

  • 设先验分布为$q(\theta)$，贝叶斯方法预测为

    $$\begin{align*} E_{q(\theta)}[y] & = \int_q f(x, \theta) q(\theta) d\theta \\ & \approx \frac 1 M \sum_{m=1}^M f(x, \theta_m) \end{align*}$$

  • $f(x, \theta_m)$：第$m$次应用丢弃方法的网络
  • $\theta_m$：对全部参数的采样

数据说明

数据模式

• 结构化数据：行数据，可用二维表逻辑表达数据逻辑、存储在数据库中

  • 可以看作是关系型数据库中一张表
  • 行：记录、元组，表示一个样本信息
  • 列：字段、属性，有清晰定义

• 非结构化数据：相对于结构化数据而言，不方便用二维逻辑表达的数据

  • 包含信息无法用简单数值表示
    • 没有清晰列表定义
    • 每个数据大小不相同
  • 研究方向
    • 社交网络数据
    • 文本数据
    • 图像、音视频
    • 数据流
  • 针对不同类型数据、具体研究方面有不同的具体分析方法，不存在普适、可以解决所有具体数据的方法

• 半结构化数据：介于完全结构化数据、完全无结构数据之间的数据

  • 一般是自描述的，数据结构和内容混合、没有明显区分
  • 树、图（XML、HTML 文档也可以归为半结构化数据）

• 结构化数据：先有结构、再有数据
• 半结构化数据：先有数据、再有结构

数据拼接

• 利用外键拼接不同来源的数据时，注意不同数据间粒度差异
  • 外键低于问题标签粒度时，考虑对数据作聚合操作再拼接
    • 保证拼接后用于训练的记录粒度和问题一致
    • 避免维度爆炸
    • 各数据来源数据厚薄不同，会改变数据分布
  • 外键高于、等于目标粒度时，可考虑直接直接连接

数据问题

稀疏特征

• 产生原因
  • 数据缺失
  • 统计数据频繁 0 值
  • 特征工程技术，如：独热编码

缺失值

产生原因

• 信息暂时无法获取、成本高
• 信息被遗漏
• 属性不存在

缺失值影响

• 建模将丢失大量有用信息
• 模型不确定性更加显著、蕴含规则更难把握
• 包含空值可能使得建模陷入混乱，导致不可靠输出

缺失利用

• 直接使用含有缺失值特征：有些方法可以完全处理、不在意缺失值

  • 分类型变量可以将缺失值、异常值单独作为特征的一种取值
  • 数值型变量也可以离散化，类似分类变量将缺失值单独分箱

• 删除含有缺失值特征

  • 一般仅在特征缺失率比较高时才考虑采用，如缺失率达到 90%、95%

插值补全

• 非模型补全缺失值

  • 均值、中位数、众数
  • 同类/前后均值、中位数、众数
  • 固定值
  • 矩阵补全
  • 最近邻补全：寻找与样本最接近样本相应特征补全

• 手动补全：根据对所在领域理解，手动对缺失值进行插补

  • 需要对问题领域有很高认识理解
  • 缺失较多时费时、费力

• 建模预测：回归、决策树模型预测

  • 若其他特征和缺失特征无关，预测结果无意义
  • 若预测结果相当准确，缺失属性也没有必要纳入数据集

• 多重插补：认为待插补值是随机的

  • 通常估计处待插补值
  • 再加上不同噪声形成多组可选插补值
  • 依据某准则，选取最合适的插补值

• 高维映射：one-hot 编码增加维度表示某特征缺失

  • 保留所有信息、未人为增加额外信息
  • 可能会增加数据维度、增加计算量
  • 需要样本量较大时效果才较好

• 压缩感知：利用信号本身具有的稀疏性，从部分观测样本中恢复原信号

  • 感知测量阶段：对原始信号进行处理以获得稀疏样本表示
    • 傅里叶变换
    • 小波变换
    • 字典学习
    • 稀疏编码
  • 重构恢复阶段：基于稀疏性从少量观测中恢复信号

异常值

• 异常值/离群点：样本中数值明显偏离其余观测值的个别值

异常值分析：检验数据是否有录入错误、含有不合常理的数据

非模型异常值检测

• 简单统计

  • 观察数据统计型描述、散点图
  • 箱线图：利用箱线图四分位距对异常值进行检测

• $3\sigma$ 原则：取值超过均值 3 倍标准差，可以视为异常值

  • 依据小概率事件发生可能性“不存在”
  • 数据最好近似正态分布

模型异常值检测

• 基于模型预测：构建概率分布模型，计算对象符合模型的概率，将低概率对象视为异常点

  • 分类模型：异常点为不属于任何类的对象
  • 回归模型：异常点为原理预测值对象
  • 特点
    • 基于统计学理论基础，有充分数据和所用的检验类型知识时，检验可能非常有效
    • 对多元数据，可用选择少，维度较高时，检测效果不好

• 基于近邻度的离群点检测：对象离群点得分由其距离 k-NN 的距离确定

  • k 取值会影响离群点得分，取 k-NN 平均距离更稳健
  • 特点
    • 简单，但时间复杂度高 $\in O(m^2)$，不适合大数据集
    • 方法对参数 k 取值敏感
    • 使用全局阈值，无法处理具有不同密度区域的数据集

• 基于密度的离群点检测

  • 定义密度方法
    • k-NN 分类：k 个最近邻的平均距离的倒数
    • DSSCAN 聚类中密度：对象指定距离 d 内对象个数
  • 特点
    • 给出定量度量，即使数据具有不同区域也能很好处理
    • 时间复杂度 $\in O^(m^2)$，对低维数据使用特点数据结构可以达到 $\in O(mlogm)$
    • 参数难以确定，需要确定阈值

• 基于聚类的离群点检测：不属于任何类别簇的对象为离群点

  • 特点
    • （接近）线性的聚类技术检测离群点高度有效
    • 簇、离群点互为补集，可以同时探测
    • 聚类算法本身对离群点敏感，类结构不一定有效，可以考虑：对象聚类、删除离群点再聚类
    • 检测出的离群点依赖类别数量、产生簇的质量

• One-class SVM

• Isolation Forest

异常值处理

• 删除样本

  • 简单易行
  • 观测值很少时，可能导致样本量不足、改变分布

• 视为缺失值处理

  • 作为缺失值不做处理
  • 利用现有变量信息，对异常值进行填补
  • 全体/同类/前后均值、中位数、众数修正
  • 将缺失值、异常值单独作为特征的一种取值

• 很多情况下，要先分析异常值出现的可能原因，判断异常值是否为真异常值

类别不平衡问题

创造新样本

• 对数据集重采样

  • 尝试随机采样、非随机采样
  • 对各类别尝试不同采样比例，不必保持 1:1 违反现实情况
  • 同时使用过采样、欠采样

• 属性值随机采样

  • 从类中样本每个特征随机取值组成新样本
  • 基于经验对属性值随机采样
  • 类似朴素贝叶斯方法：假设各属性之间相互独立进行采样，但是无法保证属性之前的线性关系

• 对模型进行惩罚

  • 类似 AdaBoosting：对分类器小类样本数据增加权值
  • 类似 Bayesian分类：增加小类样本错分代价，如：penalized-SVM、penalized-LDA
  • 需要根据具体任务尝试不同惩罚矩阵

新角度理解问题

• 将小类样本视为异常点：问题变为异常点检测、变化趋势检测

  • 尝试不同分类算法
  • 使用 one-class 分类器

• 对问题进行分析，将问题划分为多个小问题

  • 大类压缩为小类
  • 使用集成模型训练多个分类器、组合

• 需要具体问题具体分析

模型评价

• 尝试其他评价指标：准确度在不平衡数据中不能反映实际情况
  • 混淆矩阵
  • 精确度
  • 召回率
  • F1 得分
  • ROC 曲线
  • Kappa

数据量缺少

图片数据扩充

Data Agumentation：根据先验知识，在保留特点信息的前提下，对原始数据进行适当变换以达到扩充数据集的效果

• 对原始图片做变换处理

  • 一定程度内随机旋转、平移、缩放、裁剪、填充、左右翻转，这些变换对应目标在不同角度观察效果
  • 对图像中元素添加噪声扰动：椒盐噪声、高斯白噪声
  • 颜色变换
  • 改变图像亮度、清晰度、对比度、锐度

• 先对图像进行特征提取，在特征空间进行变换，利用通用数据 扩充、上采样方法

  • SMOTE

• Fine-Tuning 微调：直接接用在大数据集上预训练好的模型，在小数据集上进行微调

  • 简单的迁移学习
  • 可以快速寻外效果不错针对目标类别的新模型

特征缩放

• 正则化：针对单个样本，将每个样本缩放到单位范数
• 归一化：针对单个属性，需要用到所有样本在该属性上值

Normalizaion

归一化/标准化：将特征/数据缩放到指定大致相同的数值区间

• 某些算法要求数据、特征数值具有零均值、单位方差
• 消除样本数据、特征之间的量纲/数量级影响
  • 量级较大属性占主导地位
  • 降低迭代收敛速度：梯度下降时，梯度方向会偏离最小值，学习率必须非常下，否则容易引起宽幅震荡
  • 依赖样本距离的算法对数据量机敏感

• 决策树模型不需要归一化，归一化不会改变信息增益（比），Gini 指数变化

Min-Max Scaling

线性函数归一化：对原始数据进行线性变换，映射到 $[0, 1]$ 范围

$$X_{norm} = \frac {X - X_{min}} {X_{max} - X_{min}}$$

• 训练集、验证集、测试集都使用训练集归一化参数

Z-Score Scaling

零均值归一化：将原始数据映射到均值为 0，标准差为 1 的分布上

$$Z = \frac {X - \mu} {\sigma}$$

其他一些变换方式

• 对数变换：$X^{‘} = lg(X)$
• 反余切函数变换：$X^{‘} = \frac {2 arctan(x)} {\pi}$
• Sigmoid 变换：$X^{‘} = \frac 1 {1 + e^{-x}}$
• 模糊向量变：$X^{‘} = \frac 1 2 + \frac 1 2 sin \frac {X - \frac{max(X) - min(X)} 2} {max(X) - min(X)} * \pi$

Regularization

正则化：将样本/特征某个范数缩放到单位 1

$$\begin{align*} \overrightarrow x_i & = ( \frac {x_i^{(1)}} {L_p(\overrightarrow x_i)}, \frac {x_i^{(2)}} {L_p(\overrightarrow x_i)}, \cdots, \frac {x_i^{(d)}} {L_p(\overrightarrow x_i)})^T \\ L_p(\overrightarrow x_i) & = (|x_i^{(1)}|^p + |x_i^{(2)}|^p + \cdots + |x_i^{(d)}|^p)^{1/p} \end{align*}$$

• $L_p$：样本的 $L_p$ 范数

• 使用内积、二次型、核方法计算样本之间相似性时，正则化很有用

综述

• 特征工程：对原始数据进行工程处理，将其提炼为特征，作为输入供算法、 模型使用

  • 本质上：表示、展示数据的过程
  • 目的：去除原始数据中的杂质、冗余，设计更高效的特征以刻画求解的 问题、预测模型之间的关系
    • 把原始数据转换为可以很好描述数据特征
    • 建立在其上的模型性能接近最优
  • 方式：利用数据领域相关知识、人为设计输入变量

• 数据、特征决定了机器学习的上限，模型、算法只是逼近上限，特征越好

  • 模型选择灵活性越高：较好特征在简单模型上也能有较好 效果，允许选择简单模型
  • 模型构建越简单：较好特征即使在超参不是最优时效果也 不错，不需要花时间寻找最优参数
  • 模型性能越好
    • 排除噪声特征
    • 避免过拟合
    • 模型训练、预测更快

• 特征工程要：小步快跑、多次迭代

  • 便于及时发现问题、定位问题，如：数据穿越