Convolutional

卷积：卷积区域逐点乘积、求和作为卷积中心取值

• 用途：

  • 提取更高层次的特征，对图像作局部变换、但保留局部特征
  • 选择和其类似信号、过滤掉其他信号、探测局部是否有相应模式，如
    • sobel 算子获取图像边缘

• 可变卷积核与传统卷积核区别

  • 传统卷积核参数人为确定，用于提取确定的信息
  • 可变卷积核通过训练学习参数，以得到效果更好卷积核

• 卷积类似向量内积

特点

• 局部感知：卷积核所覆盖的像素只是小部分、局部特征

  • 类似于生物视觉中的 receptive field

• 多核卷核：卷积核代表、提取某特征，多各卷积核获取不同特征

• 权值共享：给定通道、卷积核，共用滤波器参数

  • 卷积层的参数取决于：卷积核、通道数
  • 参数量远小于全连接神经网络

• receptive field：感受野，视觉皮层中对视野小区域单独反应的神经元

  • 相邻细胞具有相似和重叠的感受野
  • 感受野大小、位置在皮层之间系统地变化，形成完整的视觉空间图

发展历程

• 1980 年 neocognitron 新认知机提出
  • 第一个初始卷积神经网络，是感受野感念在人工神经网络首次应用
  • 将视觉模式分解成许多子模式（特征），然后进入分层递阶式的特征平面处理

卷积应用

Guassian Convolutional Kernel

高斯卷积核：是实现 尺度变换 的唯一线性核

$$\begin{align*} L(x, y, \sigma) & = G(x, y, \sigma) * I(x, y) \\ G(x, y, \sigma) & = \frac 1 {2\pi\sigma^2} exp\{\frac {-((x-x_0)^2 + (y-y_0)^2)} {2\sigma^2} \} \end{align*}$$

• $G(x,y,\sigma)$：尺度可变高斯函数
• $I(x,y)$：放缩比例，保证卷积核中各点权重和为 1
• $(x,y)$：卷积核中各点空间坐标
• $\sigma$：尺度变化参数，越大图像的越平滑、尺度越粗糙

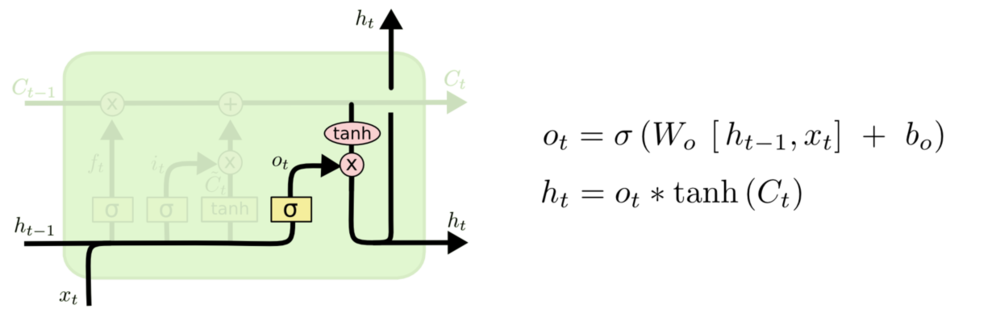
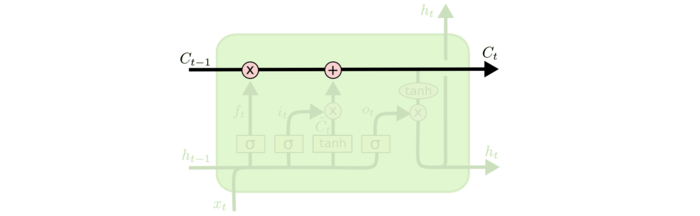
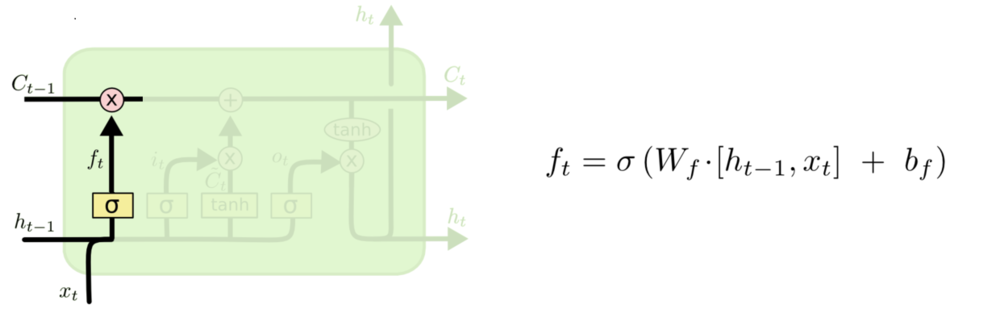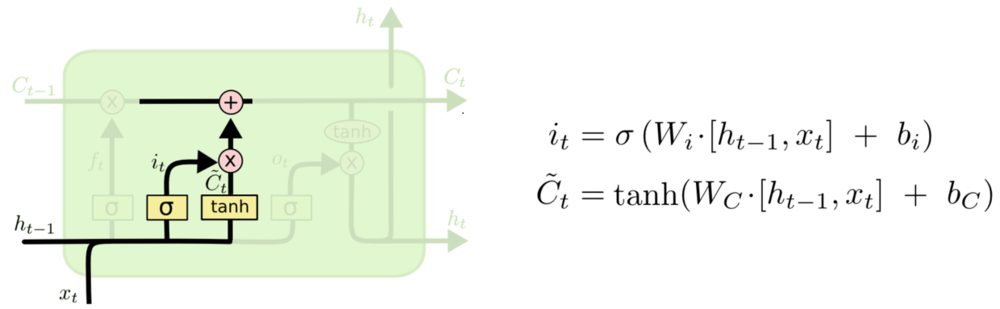Attention Machanism

注意力机制：将query、key-value映射至输出的权重生成机制

$$Attention(Q, K, V) = \phi(f_{Att}(Q, K), V)$$

• $V_{L d_v}$：value矩阵，*信息序列矩阵
• $K_{L * d_k}$：key矩阵，大部分情况即为$V$
• $Q_{L * d_k}$：query矩阵，其他环境信息
• $L, d_k, d_v$：输入序列长度、key向量维度、value向量维度
• key、value向量为$K, V$中行向量

• 合理分配注意力，优化输入信息来源

  • 给重要特征分配较大权
  • 不重要、噪声分配较小权

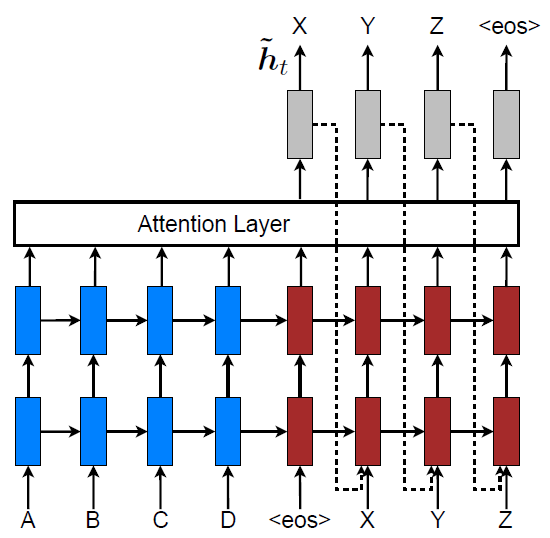
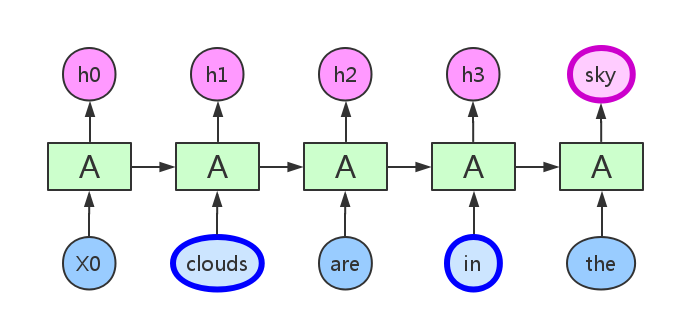
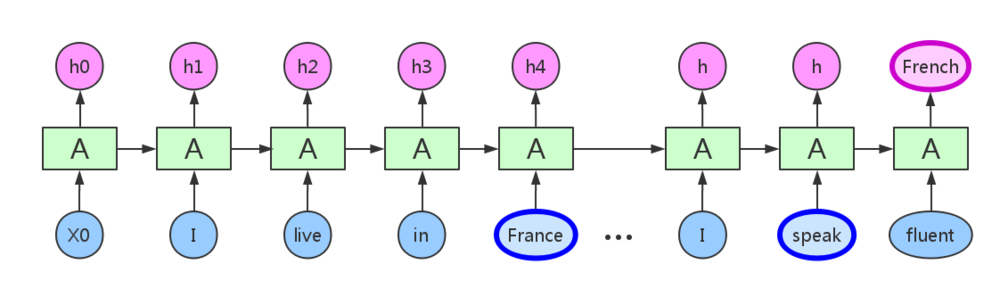
• 在不同模型间学习对齐

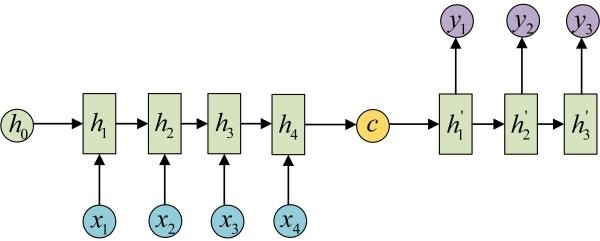
  • attention机制常联合Seq2Seq结构使用，通过隐状态对齐
  • 如：图像至行为、翻译

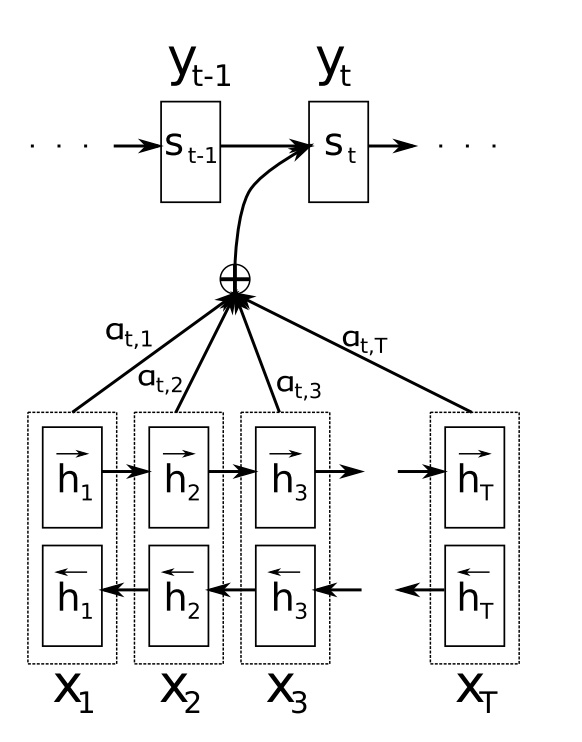
Attention Model

• Attenion机制一般可以细化如下

$$\begin{align*} c_t & = \phi(\alpha_t, V) \\ \alpha_{t} & = softmax(e_t) \\ & = \{ \frac {exp(e_{t,j})} {\sum_{k=1}^K exp(e_{t,k})} \} \\ e_t & = f_{Att}(K, Q) \end{align*}$$

• $c_t$：context vector，注意力机制输出上下文向量
• $e_{t,j}$：$t$时刻$i$标记向量注意力得分
• $\alpha_{t,i}$：$t$时刻$i$标记向量注意力权重
• softmax归一化注意力得分

• $f_{Att}$：计算各标记向量注意力得分

  • additive attention
  • multiplicative/dot-product attention：
  • local attention

  • 其参数需联合整个模型训练、输入取决于具体场景

• $\phi_{Att}$：根据标记向量注意力权重计算输出上下文向量

  • stochastic hard attention
  • deterministic soft attention

• $Q$可能包括很多信息

  • Decoder结构输出、Encoder结构输入
  • $W$待训练权重矩阵
  • LSTM、RNN等结构隐状态

Additive Attention

• 单隐层前馈网络（MLP）

  $$e_{t,j} = v_a^T f_{act}(W_a [h_{t-1}; g_j])$$

  • $h_{t-1}$：输出结构隐状态
  • $g_j$：输入结构隐状态
  • $W_a, v_a$：待训练参数
  • $f_{act}$：激活函数$tanh$、$ReLU$等

Multiplicative/Dot-product Attention

$$e_{t,j} = \left \{ \begin{array}{l} h_{t-1}^T g_j, & dot \\ h_{t-1}^T W_a g_j, & general \\ W_a h_{t-1}, & location \end{array} \right.$$

• 相较于加法attention实际应用中更快、空间效率更高 （可以利用高度优化的矩阵乘法运算）

• MLP
• 內积形式

Tricks

• 将输出作为输入引入，考虑上一次输出影响

  

• Scaled Dot-Product Attention

  $$f_{Att} = \frac {Q K^T} {\sqrt{d_k}}$$
  • 避免內积随着key向量维度$d_k$增大而增大，导致softmax 中梯度过小

Stochastic Hard Attention

hard attention：随机抽取标记向量作为注意力位置

• 注意力位置视为中间one-hot隐向量，每次只关注某个标记向量

• 模型说明

  • $f_{Att}$为随机从标记向量$a$中抽取一个
  • $\alpha$视为多元伯努利分布参数，各分量取值表示对应 标记向量被抽中概率，此时上下文向量也为随机变量

$$\begin{align*} p(s_{t,i}=1) & = \alpha_{t,i} \\ c_t & = V s \end{align*}$$

• $s$：注意力位置，中间隐one-hot向量，服从$\alpha$指定的 多元伯努利分布
• $h_i$：第$i$上下文向量

参数训练

• 参数$\alpha$不可导、含有中间隐变量$s$，考虑使用EM算法 思想求解

  $$\begin{align*} log p(y) & = log \sum_s p(s) p(y|s) \\ & \geq \sum_s p(s) log p(y|s) := L_s \\ \frac {\partial L_s} {\partial W} & = \sum_s [ \frac {\partial p(s)} {\partial W} + \frac 1 {p(y|s)} \frac {\partial p(y|s)} {\partial W}] \\ & = \sum_s p(s) [\frac {\partial log p(y|s)} {\partial W} + log p(y|s) \frac {\partial log p(s|a)} {\partial W}] \end{align*}$$

  • $L_s$：原对数似然的函数的下界，以其作为新优化目标
  • $W$：参数

• 用蒙特卡罗采样方法近似求以上偏导

  • $s$按多元伯努利分布抽样$N$次，求$N$次偏导均值

    $$\frac {\partial L_s} {W} \approx \frac 1 N \sum_{n=1}^N [\frac {\partial log p(y|\tilde s_n)} {\partial W} + log p(y|\tilde s_n) \frac {\partial log p(\tilde s_n|a)} {\partial W}]$$

    • $\tilde s_n$：第$n$次抽样结果

  • 可对$p(y|\tilde s_n)$进行指数平滑减小估计方差

Deterministic Soft Attention

soft attention：从标记向量估计上下文向量期望

• 考虑到所有上下文向量，所有标记向量加权求和上下文向量
• 模型说明
  • $f_{Att}$计算所有标记向量注意力得分
  • $\alpha$可视为个标记向量权重

$$E_{p(s_t)} [c_t] = \sum_{i=1}^L \alpha_{t,i} a_i$$

• 模型光滑可微：可直接用反向传播算法训练

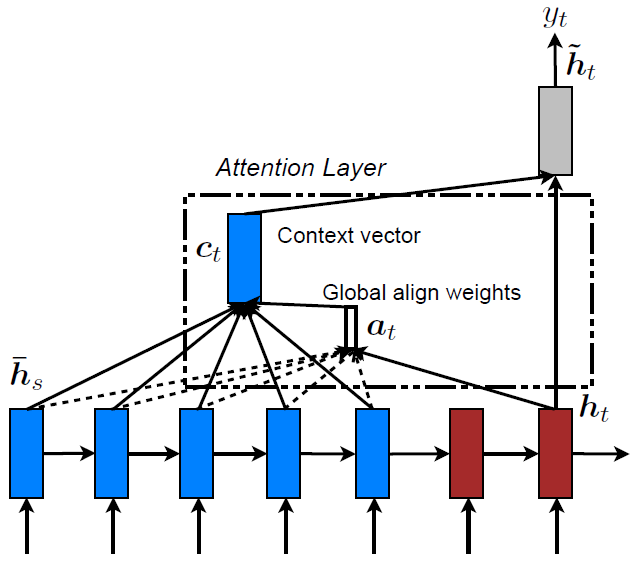
Local Attention

local attention：从所有标记向量中选取部分计算soft attention

• 可以视为hard、soft attention结合
  • hard attention选取标记向量子区间，避免噪声干扰
  • soft attention加权求和，方便训练

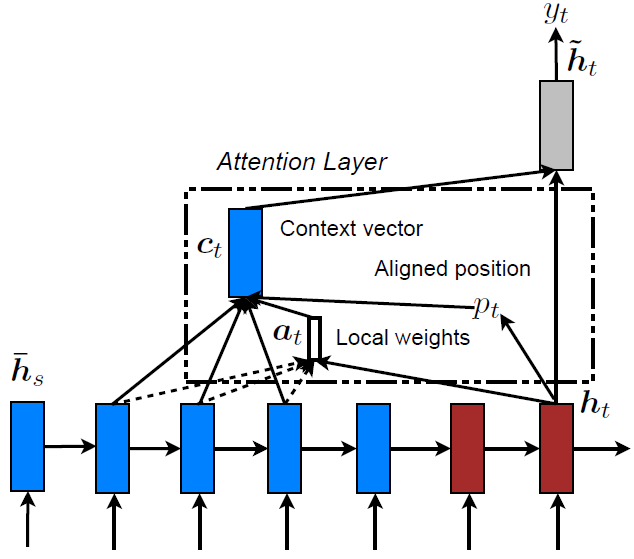
子区间选取

• 为目标$t$选取对齐位置$p_t$，得到子区间$[p_t-D, p_t+D]$ （$D$为经验选取）

• monotonic alignment：直接设置$p_t=t$

• predictive alignment：

  $$p_t = S sigmoid(v_p^T tanh(W_p h_t))$$

  • $W_p, v_p$：待学习参数

• 可以使用高斯分布给注意力权重加权，强化$p_t$附近标记向量 （根据经验可以设置$\sigma = \frac D 2$） $$\alpha_{t,j} = softmax(e_{t,j}) exp(-\frac {(j - p_t)^2} {2\sigma^2})$$

Self Attention

Self Attention/Intra-Attention：关联同一序列内不同位置、 以学习序列表示的attenion机制

• 类似卷积、循环结构

  • 将不定长的序列映射为等长的另一序列
  • 从序列中提取高层特征

• 特点

  • 类似卷积核，多个self attention可以完全并行
  • 无需循环网络多期传递信息，输入序列同期被处理
  • 可使用local attention机制限制计算复杂度

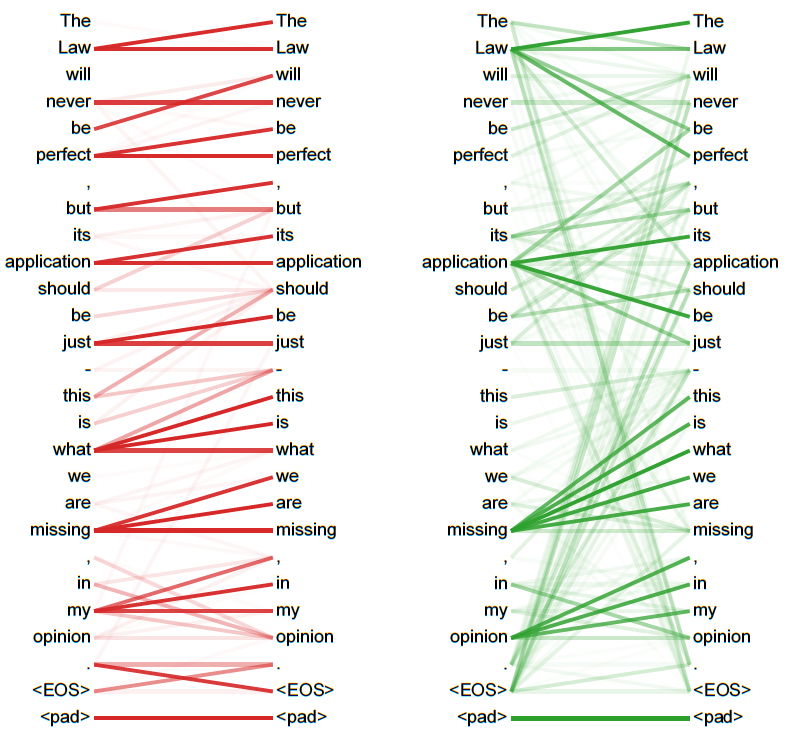
Multi-Head Attention

Multi-Head Attention：从相同输入、输出序列学习多个 attention机制

$$\begin{align*} MultiHead(X) & = Concat(head1, ..., head_h) W^O \\ head_i & = Attention(QW_i^Q, KW_i^K, VW_i^V) \end{align*}$$

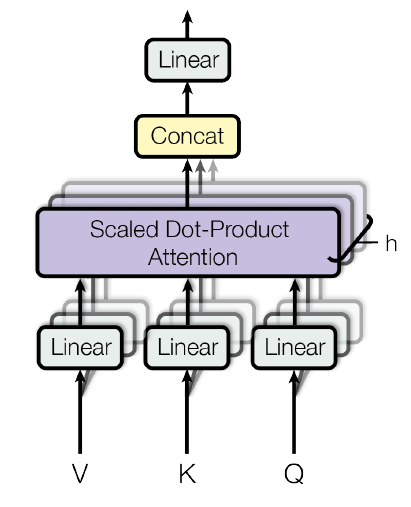
• $Q, K, V$：元信息矩阵，据此训练多组query、key-value， 一般就是原始输入序列矩阵

• 可以并行训练，同时从序列中提取多组特征

人工交互作用层

交互作用层：人工设置特征之间交互方式

Flatten Layer

展平层：直接拼接特征，交互作用交由之后网络训练

$$f_{Flat}(V_x) = \begin{bmatrix} x_1 v_1 \\ \vdots\\ x_M v_M \end{bmatrix}$$

• $V_x$：特征向量集合

• 对同特征域特征处理方式
  • 平均
  • 最大

二阶交互作用

二阶交互作用层：特征向量之间两两逐元素交互

• 交互方式
  • 逐元素
    • 乘积
    • 求最大值：无
  • 按向量
• 聚合方式
  • 求和
    • 平权
    • Attention加权
  • 求最大值：无

Bi-Interaction Layer

Bi-Interaction Layer：特征向量两两之间逐元素乘积、求和

$$\begin{align*} f_{BI}(V) & = \sum_{i=1}^M \sum_{j=i+1}^M v_i \odot v_j \\ & = \frac 1 2 (\|\sum_{i=1}^M v_i\|_2^2 - \sum_{i=1}^M \|v_i\|_2^2) \end{align*}$$

• $\odot$：逐元素乘积

• 没有引入额外参数，可在线性时间$\in O(kM_x)$内计算
• 可在低层次捕获二阶交互影响，较拼接操作更informative
  • 方便学习更高阶特征交互
  • 模型实际中更容易训练

Attention-based Pooling

Attention-based Pooling：特征向量两两之间逐元素乘积、加权 求和

$$f_{AP}(V) & = \sum_{i=1}^M \sum_{j=i+1}^M \alpha_{i,j} (v_i \odot v_j)$$

• $\alpha_{i,j}$：交互作用注意力权重，通过注意力网络训练

Embedding

嵌入层：将高维空间中离散变量映射为低维稠密 embedding 向量表示

• embedding 向量更能体现样本之间关联

  • 內积（內积）体现样本之间接近程度
  • 可通过可视化方法体现样本差异

• embedding 向量更适合某些模型训练

  • 模型不适合高维稀疏向量
  • embedding 向量矩阵可以联合模型整体训练，相当于提取特征
  • embedding 向量也可能类似迁移学习独立训练之后直接融入模型中

• Embedding：将度量空间中对象映射到另个（低维）度量空间，并尽可能保持不同对象之间拓扑关系，如 Word-Embedding

Embedding表示

• 特征不分组表示

  $$\begin{align*} \varepsilon_x & = E x \\ & = [x_1v_1, x_2v_2, \cdots, x_Mv_M] \\ & = [x_{M_1} v_{M_1}, \cdots, x_{M_m} v_{M_m}] \end{align*}$$

  • $E$：embedding向量矩阵
  • $M$：特征数量
  • $v_i$：$k$维embedding向量
  • $x_i$：特征取值，对0/1特征仍等价于查表，只需考虑非0特征

    • $x_{M_i}$：第$j$个非0特征，编号为$M_i$
    • $m$：非零特征数量

  • $\varepsilon_x$：特征向量集合

• 特征分组表示

  $$\begin{align*} \varepsilon_x & = [V_1 g_1, V_2 g_2, \cdots, V_G g_G] \end{align*}$$

  • $G$：特征组数量
  • $V_i$：第$i$特征组特征向量矩阵
  • $g_i$：第$i$特征组特征取值向量

池化/下采样

池化：在每个区域中选择只保留一个值

• 用于减小数据处理量同时保留有用的信息

  • 相邻区域特征类似，单个值能表征特征、同时减少数据量

• 保留值得选择有多种

  • 极值
  • 平均值
  • 全局最大

• 直观上

  • 模糊图像，丢掉一些不重要的细节

Max Pooling

最大值采样：使用区域中最大值作为代表

Average Pooling

平均值采样：使用池中平均值作为代表

Recurrent Neural Network

RNN：处理前后数据有关联的序列数据

• 左侧：为折叠的神经网络，右侧：按时序展开后的网络
• $h$：循环隐层，其中神经元之间有权连接，随序列输入上一期 隐层会影响下一期
• $o$、$y$：输出预测值、实际值
• $L$：损失函数，随着时间累加

• 序列往往长短不一，难以拆分为独立样本通过普通DNN训练

结构

• 普通的DNN：固定大小输入得到固定输出
• 单个输入、序列输出：输入图片，得到描述文字序列
• 序列输入、单个输出：情感分析
• 异步序列输入、输出：机器翻译
• 同步序列输入、输出：视频帧分类

权值连接

• 循环隐层内神经元之间也建立权连接，即循环

  • 基础神经网络只在层与层之间建立权值连接是RNN同普通DNN 最大不同之处

• 循环隐层中神经元只会和其当前层中神经元建立权值连接

  • 即不受上期非同层神经元影响
  • 循环隐层中神经元$t$期状态$h^{(t)}$由当期输入、 $h^{(t-1)}$共同决定

• Gated Feedback RNN：循环隐层会对下期其他隐层产生影响

逻辑结构

• RNN网络实际结构是线性、折叠的，逻辑结构则是展开的结构， 考虑RNN性质应该在展开的逻辑结构中考虑

• 序列输入

  • 实际结构：依次输入
  • 逻辑结构：里是整体作为一次输入、才是一个样本，损失、 反向传播都应该以完整序列为间隔

• 权值共享

  • 实际结构：不同期的权值实际是同一组
  • 逻辑结构：称为权值共享

• 重复模块链

  • 实际结构：同一个模块
  • 逻辑结构：不同期模块之间信息流动形成链式形式

信息传递

• RNN循环层中信息只能由上一期直接传递给下一期

• 输入、输出相关信息间隔较近时，普通RNN可以胜任

  

• 当间隔很长，RNN理论上虽然能够处理，但由于梯度消失问题， 实际上长期依赖会消失，需要LSTM网络

  

Forward Propogation

• $h^{(t)} = \sigma(z^{(t)}) = \sigma(Ux^{(t)} + Wh^{(t-1)} +b )$

  • $\sigma$：RNN激活函数，一般为$tanh$
  • $b$：循环隐层偏置

• $o^{(t)} = Vh^{(t)} + c$

  • $c$：输出层偏置

• $\hat{y}^{(t)} = \sigma(o^{(t)})$

  • $\sigma$：RNN激活函数，分类时一般时$softmax$

Back-Propogation Through Time

BPTT：训练RNN的常用方法

• 本质仍然是BP算法，但是RNN处理序列数据，损失随期数累加， 即计算梯度时使用最终损失$L = \sum_{t=1}^\tau L^{(t)}$

• 对循环层中参数，梯度沿着期数反向传播，第t期反向传播时， 需要逐级求导

• 序列整体作为一次输入，进行一次反向传播
• 理论上可以漂亮的解决序列数据的训练，但是和DNN一样有梯度 消失的问题，尤其是序列很长时，所以一般不能直接应用

非循环层

• $\frac{\partial L}{\partial c}$

  $$\begin{align*} \frac{\partial L}{\partial c} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}}{\partial c} & = \sum_{t=1}^{\tau}\frac{\partial L^{(t)}} {\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} & = \sum_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)} \end{align*}$$

  • $L^{(t)} = \frac 1 2 (\hat{y}^{(t)} - y^{(t)})^2$： 使用平方损失

• $\frac{\partial L}{\partial V}$

  $$\begin{align*} \frac{\partial L}{\partial V} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}}{\partial V} & = \sum_{t=1}^{\tau} \frac{\partial L^{(t)}} {\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial V} & = \sum_{t=1}^{\tau}(\hat{y}^{(t)} - y^{(t)}) (h^{(t)})^T \end{align*}$$

循环层

• 为方便定义： $\delta^{(t)} = \frac {\partial L} {\partial h^{(t)}}$

• $\delta^{(t)}$

  $$\begin{align*} \delta^{(t)} & = \frac {\partial L} {\partial h^{(t)}} \\ & = \frac{\partial L}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial h^{(t+1)}} \frac{\partial h^{(t+1)}}{\partial h^{(t)}} & = V^T(\hat{y}^{(t)} - y^{(t)}) + W^T\delta^{(t+1)}diag(1-h^{(t+1)})^2) \end{align*}$$

  • $\frac{\partial h^{(t+1)}}{\partial h^{(t)}} = diag(1-h^{(t+1)})^2)$ ：$tanh(x)$梯度性质
  • $h^{(t)}(t<\tau)$梯度：被后一期影响（反向传播），需递推

• $\delta^{(\tau)}$

  $$\begin{align*} \delta^{(\tau)} & = \frac{\partial L}{\partial o^{(\tau)}} \frac{\partial o^{(\tau)}}{\partial h^{(\tau)}} & = V^T(\hat{y}^{(\tau)} - y^{(\tau)}) \end{align*}$$

  • $\tau$期后没有其他序列，可以直接求出

• $\frac{\partial L}{\partial W}$

  $$\begin{align*} \frac{\partial L}{\partial W} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial W} & = \sum_{t=1}^{\tau}diag(1-(h^{(t)})^2) \delta^{(t)}(h^{(t-1)})^T \end{align*}$$

  • 需要由$\sigma^{(t)}$累加得到

• $\frac{\partial L}{\partial b}$

  $$\begin{align*} \frac{\partial L}{\partial b} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial b} & = \sum_{t=1}^{\tau} diag(1-(h^{(t)})^2)\delta^{(t)} \end{align*}$$

• $\frac{\partial L}{\partial U}$

  $$\begin{align*} \frac{\partial L}{\partial U} & = \sum_{t=1}^{\tau} \frac{\partial L}{\partial h^{(t)}} \frac{\partial h^{(t)}}{\partial U} & = \sum_{t=1}^{\tau}diag(1-(h^{(t)})^2) \delta^{(t)}(x^{(t)})^T \end{align*}$$

}$$

Long Short Term Memory

LSTM：通过刻意设计、默认可以学习长期依赖信息的RNN网络

• LSTM中每个重复的模块（层）称为细胞

  • 细胞结构经过特殊设计，相较于准RNN简单细胞结构能较好 保留长时信息

• 多个LSTM细胞可以组成block，其中细胞门权值共享

  • block中各个细胞状态不同
  • 这个是同时刻、不同层的真权值共享，类似CNN中的卷积核
  • 减少参数个数，效率更高

• long term memory：长期记忆，参数
• short term memory：短期记忆，数据流
• long short term memory：长[的]短期记忆，细胞状态

LSTM标准细胞结构

$$\begin{align*} i^{(t)} & = \sigma(W_i[x^{(t)}, h^{(t-1)}], b_i), & input gate \\ f^{(t)} & = \sigma(W_f[x^{(t)}, h^{(t-1)}], b_f), & forget gate \\ o^{(t)} & = \sigma(W_o[x^{(t)}, h^{(t-1)}], b_o), & output gate \\ \tilde C^{(t)} & = tanh((W_c[x^{(t)}, h^{(t)}])), & memory alternates \\ C^{(t)} & = f^{(t)} \odot c^{(t-1)} + i^{(t)} \odot c^{(t)}, & new memory \\ h^{(t)} & = o^{(t)} \odot tanh(c^{(t)}), & output \end{align*}$$

• $W_i, b_i, W_f, b_f, W_o, b_o$：输入门、遗忘门、输出门 参数
• $\odot$：逐项乘积
• $x_t$：第$t$期输入
• $i^{(t)}$：输出门权重，决定需要更新的信息
• $f^{(t)}$：遗忘门权重，决定需要遗忘的信息
• $o^{(t)}$：输出门权重，决定需要输出的信息
• $h^{(t-1)}$：第$t-1$期细胞状态输出
• $\tilde C_t$：第$t$期更新备选内容
• $C^{(t)}$：第$t$期更新完成后细胞状态

• 输入、遗忘、输出门特点

  • 当期输入$x^{(t)}$、上期输出$h^{(t-1)}$作为输入
  • sigmoid作为激活函数，得到$[0,1]$间控制、权重向量
    • 1：完全保留
    • 0：完全舍弃

• 细胞状态、输出特点

  • tanh作激活函数，得到$[-1,1]$间信息向量
    • $h^{(t-1)}, x^t$：备选更新信息输入
    • $C^{(t-1)}$：输出信息输入
  • 与门限权重逐项乘积确定最终遗忘、输入、输出

  • 细胞状态选择（候选、输出）都是使用双曲正切激活，应该 是为了有正由负

Gates

• Forget Gate：遗忘门，决定要从细胞状态中舍弃的信息

  

• Input Gate：输入门，决定向细胞状态中保留的信息

  

• Ouput Gate：输出门，决定从细胞状态中输出的信息

  

Cell State

细胞状态：LSTM中最重要的核心思想

• 随着时间流动，承载之前所有状态信息，代表长期记忆

  • 类似于传送带，直接在整个链上运行，只有少量线性交互
  • 信息其上流派很容易保持不变
  • 通过“三个门”保护、控制

• LSTM可以保证长短时记忆可以理解为

  • $C_t$中历史信息比重由$f^{(t)}$确定
  • $f^{(t)}$趋近于1时历史信息能较好的保留

Gated Recurrent Unit

$$\begin{align*} r^{(t)} & = \sigma(W_r [h^{(t-1)}, x^{(t)}] + b_r), & reset gate \\ z^{(t)} & = \sigma(W_z [h^{(t-1)}, x^{(t)}] + b_z), & update gate \\ \tilde h^{(t)} &= tanh(W_h [r^{(t)} h^{(t-1)}, x^{(t)}]), & memory alternates\\ h^{(t)} & = (1 - z^{(t)}) \odot h^{(t-1)} + z^{(t)} \odot \tilde h^{(t)}, & new memory \end{align*}$$

• $W_r, b_r, W_z, b_z$：重置门、更新门参数
• $h^{(t)}$：原细胞状态、隐层输出合并
• $\tilde{h}_t$：第$t$期更新备选信息
• $r^{(t)}$：重置门权重输出，重置上期状态$h_{t-1}$再作为更新 门输入
• $z^{(t)]$：更新门权重输出，当期状态$ht$中$h{t-1}$、 $\tilde{h}_t$占比（遗忘、更新的结合）

• 合并细胞状态、隐层输出
• 合并遗忘门、输出门为更新门

其他变体结构

Vanilla LSTM

• Peephole Connection：细胞状态也作为3个门中sigmoid的 输入，影响控制向量的生成

Coupled Input and Forget Gate

• $1-f_i$代替$i_t$，结合遗忘门、输入门

结构比较

在Vanilla LSTM基础上的8个变体在TIMIT语音识别、手写字符识别、 复调音乐建模三个应用中比较

• No Input Gate：NIG，没有输入门
• No Forget Gate：NFG，没有遗忘门
• No Output Gate：NOG，没有输出门
• No Input Acitivation Function：NIAF，输入门没有tanh 激活
• No Output Activation Function：NOAF，输出门没有tanh 激活
• No Peepholes：NP，普通LSTM
• Coupled Input and Forget Gate：CIFG，遗忘、输出门结合
• Full Gate Recurrence：FGR，所有门之间有回路

• Vanilla LSTM效果均良好，其他变体没有性能提升

• 细胞结构

  • 遗忘门、输入门是最重要的部分
    • 遗忘门对LSTM性能影响十分关键
    • 输出门对限制无约束细胞状态输出必要
  • CIFG、NP简化结构，单对结果没有太大影响

• 超参

  • 学习率、隐层数量是LSTM主要调节参数
    • 两者之间没有相互影响，可以独立调参
    • 学习率可以可以使用小网络结构独立校准
  • 动量因子影响不大
  • 高斯噪声的引入有损性能、增加训练时间

?时间

Seq2Seq

Seq2Seq/Encoder-Decoder：允许任意长度序列输入、输出学习

$$\begin{align*} p(y_1, \cdots, y_{T^{'}} | x_1, \cdots, x_T) & = \prod_{t=1}^T p(y_t|c, y_1, \cdots, y_{t-1}) \\ c & = q(\{h_1, \cdots, h_T\}) \\ h_t & = f(x_t, h_{t-1}) \end{align*}$$

• $T^{‘} \neq T$：输出序列长度、输入序列长度
• $p(y_t|\cdots)$：一般为softmax函数计算字典中各词概率
• $c$：定长向量
• $h_t$：隐状态
• $q$：将隐状态映射为定长向量存储信息，如： $q(\cdots) = h_T$
• $f$：根据输入映射为隐状态，如：RNN、LSTM

实现策略

• encoder：将输入序列映射为定长向量
• decoder：将该定长向量映射为目标输出 （通过将联合概率有序分解来定义翻译概率）

• RNN：以内部隐状态作为定长向量存储输入信息

  • 理论上可实现在定长向量中存储相关信息、再解码
  • 但由于长时梯度消失，实际难以训练

• LSTM：类似RNN在内部隐状态中存储信息

  • 学习长时依赖更有效、容易训练

Seq2Seq with Attention

• 采用LSTM、RNN结构的Seq2Seq结构很难将输入序列转化为定长 向量而保存所有有效信息

  • 序列末尾对定长向量影响更大，难以学习长距离依赖
  • 随着输入序列长度增加，预测效果显著下降

• 使用Attention机制的Seq2Seq无需多期迭代传递信息，不存在 长距离依赖

BiRNN2RNN with Attention

$$\begin{align*} p(y_t | y_1, \cdots, y_{t-1}, x) & = g(y_{t-1}, s_t, c_t) \\ s_t & = f(s_{t-1}, y_{t-1}, c_t) \\ c_t & = \sum_{j=t}^T \alpha_{j=1}^T \alpha_{t,j} h_j \\ \alpha_{t,j} & = softmax(e_{t,j}) \\ & = \frac {exp(e_{t,j})} {\sum_{k=1}^T exp(e_{t,k})} \\ e_{t,j} & = a(s_{t-1}, h_j) \end{align*}$$

• $y_t$：当前$t$时刻输出
• $p(y_t|\cdots)$：$t$时刻输出条件概率
• $s_t$：解码器$t$时刻隐状态
• $h_j$：编码器$j$时刻隐状态
• $c_t$：expected annotation，对输出$t$的上下文向量
• $T$：输入序列长度
• $e{t,j}, \alpha{t,j}$：输入$j$对输出$t$重要性，反映 模型注意力分布
• $a$：alignment model，输入输出相关性模型，同整个系统 联合训练的前向神经网络，attention机制核心

• 编码器：Bi-RNN
• 解码器：attention机制加权的RNN