Coordinate Descent

坐标下降

坐标下降法：在当前点处延一个坐标方向进行一维搜索以求得函数 的局部极小值

• 非梯度优化算法，但能提供超过一阶的信息
  • SMO算法就是两块贪心坐标下降

说明

• 优化方向从算法一开始就固定，如：选择线性空间中一组基作为 搜索方向

• 循环极小化各坐标方向上目标函数值，即：若$x^k$给定，则

  $$x_i^{(k+1)} = \arg\min_{x \in R} f(x_1^{k+1}, \cdots, x_{i-1}^{k+1}, x, x_{i+1}^{k}, \cdots, x_n^k)$$

  • $k$：第k轮迭代
  • $i$：某轮迭代中更新第i个方向

• 对初始值为$X_0$得到迭代序列$X_1, \cdots, X_n$，对精确 一维搜索类似最速下降有

  $$F(X_0) \geq F(X_1) \geq \cdots \geq F(x_n)$$

• 若某轮迭代中目标函数无法被有优化，说明已经达到驻点

Adaptive Coordinate Descent

自适应坐标下降：变换坐标系使得在考虑目标函数的情况下，新坐标 间尽可能不相关

• 对非可拆分函数（可加？），算法可能无法在较小迭代步数中 求得最优解

  • 可采用适当坐标系加速收敛，如：主成分分析进行自适应 编码
  • 性能远超过传统坐标下降算法，甚至可以达到梯度下降的 性能

  

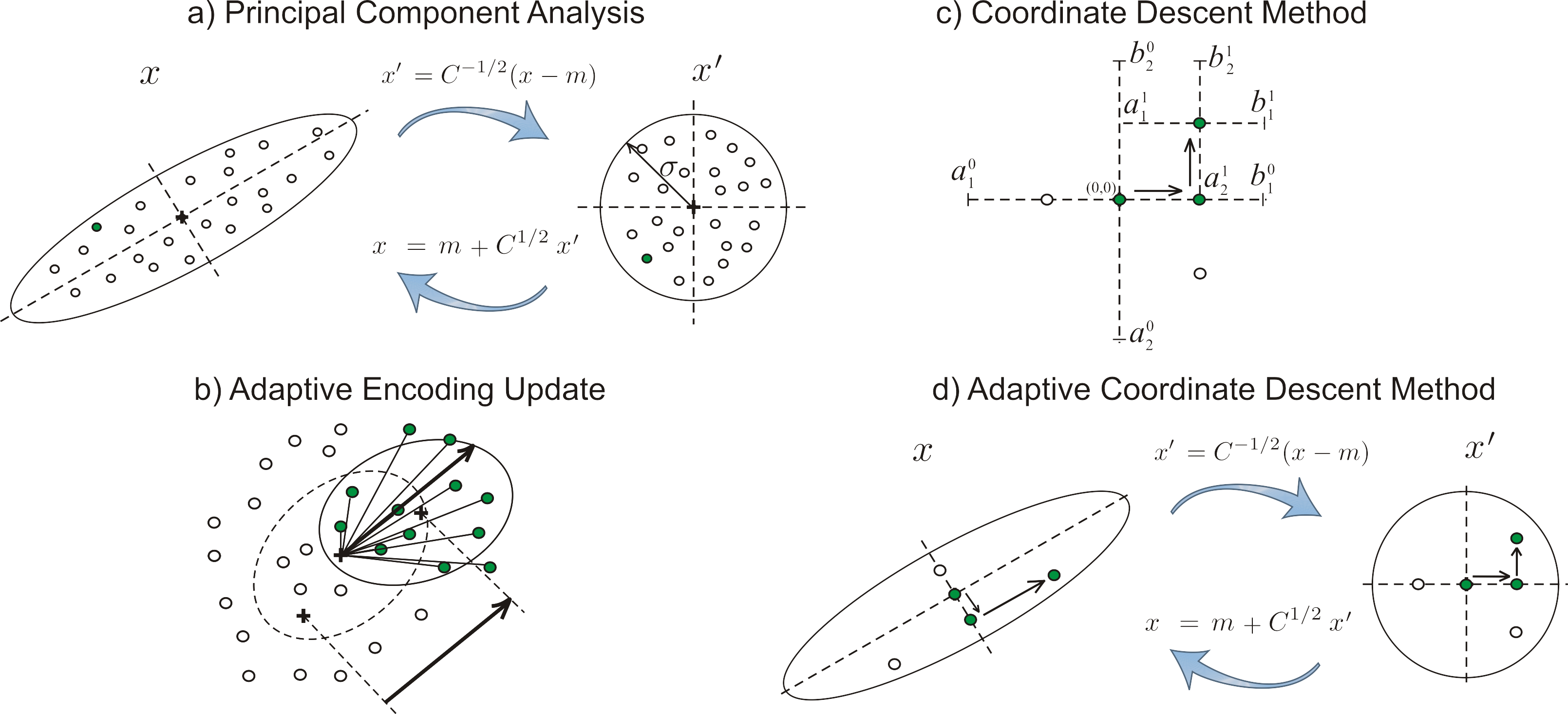
• 自适应坐标下降具有以下特性，和最先进的进化算法相当

  • 缩放不变性
  • 旋转不变性

Block Coordinate Descent

块坐标下降：在当前点处在一个超平面内方向进行搜索以求得函数 的局部极小值

• 即同时更新一组坐标的坐标下降

例

Lasso求解

• 目标函数

  $$L(x) = RSS(x) + \lambda \|x\|_1 = \frac 1 2 (Ax - y)^T(Ax - y) + \lambda \|x\|_1$$

• RSS求导

  $$\begin{align*} \frac {\partial RSS} {\partial x} & = (Ax - y)^T A \\ (\frac {\partial RSS} {\partial x})_i & = (Ax - y)^T A_{:i} \\ & = (Ax_{i0} - y)^T A_{:i} + x_i A_{:i}^T A_{:i} \\ & = z_i + \rho_i x_i \end{align*}$$

  • $(\frac {\partial RSS} {\partial x})_i$：RSS对$x$ 导数第$i$分量，即对$x_i$偏导
  • $A_{:i}$：$A$第$i$列
  • $x_{i0}$：$x$第$i$分量置零
  • $zi = (Ax{i0} - y)^T A_{:i}$
  • $\rhoi = A{:i}^T A_{:i}$

• 则$x_i$整体次梯度为

  $$\frac {\partial L} {\partial x_i} = z_i + \rho_i x_i + \left \{ \begin{array}{l} -\lambda, & x_i < 0 \\ [-\lambda, \lambda], & x_i = 0 \\ \lambda, & x_i > 0 \end{array} \right.$$

• 分类讨论：令整体次梯度为0求解$x_i$、回带确定参数条件

  $$x_i = \left \{ \begin{array}{l} \frac {-z_i + \lambda} {\rho_i}, & z_i > \lambda \\ 0 , & -\lambda < z_i < \lambda \\ \frac {-z_i - \lambda} {\rho_i}, & z_i < -\lambda \end{array} \right.$$

  • 此算子也称soft threshholding