Hashing
Hashing Table
- 哈希表/散列表:可根据哈希值直接访问的数据结构
原理:以哈希值做为地址,缩小搜索空间、提高查找效率
- 使用哈希函数为每个键计算哈希值,得到位于 $0, \cdots, m-1$之间整数
- 按照哈希值把键分布在$H[0, \cdots, m-1]$哈希表中
- 查找匹配键时,以查找键哈希值作为起点在哈希表中 搜索
应选择合适的哈希函数、哈希表长度,尽量把键尽量均分在 哈希表中
- 哈希函数$hash$:参见math_algebra/#todo
- 对闭散列:减少冲突
- 对开散列:避免数据集中
- 散列表长度$m$:常为质数(方便双散列)
- 哈希函数$hash$:参见math_algebra/#todo
Load Factor
负载因子:$\alpha = \frac {noempty} {m}$
- $m$:哈希表中slots数量(长度)(哈希桶数量)
- $noempty$:非空数量
闭散列:负载因子反映哈希表冲突可能性、查找效率
- 负载因子过小:冲突可能性小,查找效率高,但浪费空间
- 负载因子过大:冲突可能性大,查找效率低,空间利用率高
- 负载因子取值最大为1
- 应适当平衡负载因子,负载因子接近1时重散列,避免冲突 过多影响查找效率
- Java中
HashMap初始负载值为0.75
开散列:负载因子反映查找效率
- 但应该无法反映冲突可能性(也无必要)
- 开散列往往被用于应对大规模数据,冲突总是存在
- 查找效率更多取决于数据(哈希值)偏倚程度
- 负载因子可以大于1
- 但应该无法反映冲突可能性(也无必要)
应用
- 字典/映射实现:cs_algorithm/data_structure/set
Open Addressing
闭散列/开放寻址:所有键存储在散列表本身中,不扩展存储空间
哈希表$m$至少要和哈希键数量$n$一样大
冲突问题解决:根据一定规则计算下个地址
cluster:聚合,散列表接近满时,一序列连续单元格被占据
- 线性探查性能恶化,操作效率降低
- 聚合越来的越大时,新元素插入聚类可能性增加
- 聚合可能被新插入元素连接,导致更大程度聚合
增量类型
增量类型:碰撞发生后,根据一定规则对原哈希值修正
- $d_i = i$:linear probing,线性探查
- $d_i = i^2, -i^2$:quadratic probing,二次探查
- $d_i = 伪随机数$:伪随机探查
- $d_i = i hash_2(K), i=0,1,2,\cdots$:double hashing* ,再散列法
- 再散列法说明:为保证哈希表中每个位置被探查,增量$s(K)$
必须互质
- $m$为质数时自动满足
- 文献推荐:$s(K) = m - 2 - K mod (m-2)$
- 对较小散列:$s(K) = 8 - (K mod 8)$
- 对较大散列:$s(K) = K mod 97 + 1$
操作
插入:依次检查哈希值$h(K)$、探查目标序列,直至找到空 单元格放置键
查找:给定查找键K,计算哈希值$h(K)$、探查目标序列,比较 K和单元格中键值
- 若查找到匹配键,查找成功
- 遇到空单元格,查找失败
删除:延迟删除,用特殊符号标记曾经被占用过、现被删除 的位置
- 不能直接删除,否则的中间出现空单元格,影响查找正确性
算法效率
成功查找访问次数: $S \approx \frac 1 2 (1+\frac 1 {(1-\alpha)})$
失败查找访问次数: $U \approx \frac 1 2 [1+\frac 1 {(1-\alpha)^2}]$
- 简化版本近似结论(散列规模越大,近似结论越正确)
- 无法避免散列表趋满时性能恶化
- 再哈希法数学分析困难,经验表明优秀的散列函数(两个), 性能较线性探查好
Multi Hashing
多重哈希:使用一组哈希函数$h_0,\cdots,h_n$依次计算哈希值, 确定插入、查找地址
- 类似增量类型方法,仅各次地址独立使用哈希函数计算
增大空间
Rehashing
重散列:扫描当前表,将所有键重新放置在更大的表中
- 散列表趋满时唯一解决办法
Overflow Area
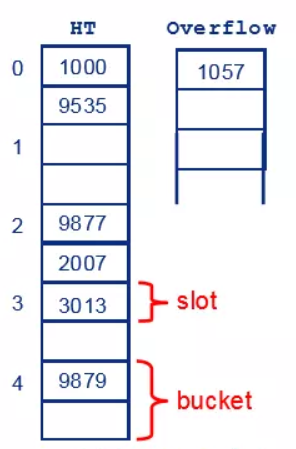
建立公共溢出区:将哈希表分为基本表、溢出表两部分
- 将发生冲突的元素都放入溢出区
- 基本表中可以考虑为为每个哈希值设置多个slots
- 即基本表直接存储哈希桶
Chaining
开散列/分离链:哈希表作为目录,使用额外数据空间组织哈希键
拉链法/分桶法
拉链法/分桶法:哈希表作为目录项存储指向hash桶的指针,hash桶 中存储哈希键
目录项表:顺序表,连续存储空间
- 可以通过hash值在常数时间内定位:一般其索引位置就是 hash值
- 目录项越多,数据分布相对越稀疏、碰撞概率越小、效率 越高
hash桶:存储具有相同哈希值元素的顺序表
- 目录项存储chain为顺序表:每个链即为hash桶
- 目录项存储chain为顺序表链:链中每个顺序表为hash桶
- 即每个目录项对应多个hash值,链接多个hash桶
操作
- 查找
- 对查找键K,使用同样散列函数计算键散的函数值$h(K)$
- 遍历相应单元格附着链表,查找是否存在键K
- 插入:计算键对应桶,在链表尾部添加键即可
- 删除:查找需要删除的键,从链表中移除即可
算法效率
效率取决于链表长度,而链表长度取决于字典、散列表长度 和散列函数质量
- 成功查找需要检查指针次数$S = 1 + \alpha / 2$
- 不成功查找需要检查指针次数$U = \alpha$
- 计算散列函数值是常数时间操作
- 若n和m大致相等,平均情况下$\in \Theta(1)$
算法查找的高效是以额外空间为代价的
Perfect Hashing
完美哈希:采用两级全域哈希,目录项链接独立哈希表的拉链哈希表
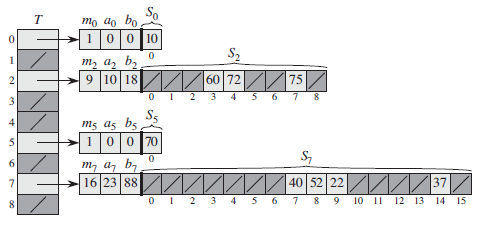
二级哈希表开头部分存储哈希表元信息
- $m = n^2$:哈希表槽数,$n$为映射至该槽元素数量 (此时由全域哈希性质:冲突次数期望小于0.5)
- $a, b$:全域哈希参数
复杂度
- 时间复杂度:最坏情况下查找为$O(1)$
- 空间复杂度:期望空间为线性 $E(\sum_{i=1}^{m-1} \theta(n_i^2) = \theta(n)$
- 完美哈希没有冲突的概率至少为0.5
- 全域哈希参见math_algebra/hash_funcs
Dynamic Hashing
动态hash:在hash表中元素增加同时,动态调整hash桶数目
- 在原hash表基础上进行动态桶扩展
- 不需要遍历表元素重复执行插入操作
- 开散列法在大规模、在线数据的扩展
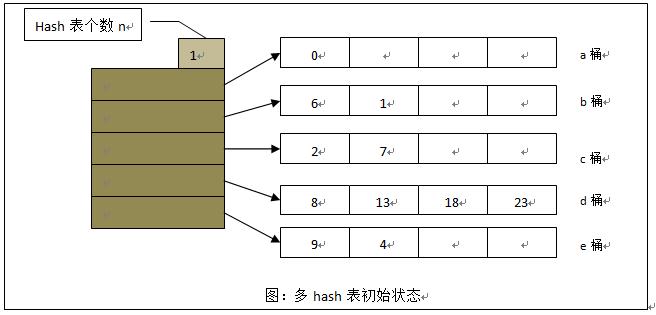
多hash表
多hash表:通过建立多个hash表的方式扩展原hash表
- 思想、实现简单
- 占用空间大,数据分布偏斜程度较大时,桶利用率不高
实现
操作时需要考虑多个hash表
插入
- 若存在hash相应桶中存在空闲区域,直接插入
- 否则分裂,新建hash表,插入元素至空闲区域
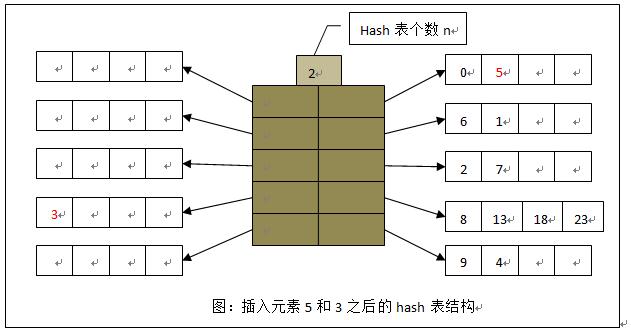
- 若存在hash相应桶中存在空闲区域,直接插入
查找:需要查找所有hash表相应桶才能确定
- 当表中元素较多时,可以考虑并行执行查找操作
删除操作:若删除元素导致某hash表空,可考虑删除该表
可扩展动态hash
可扩展动态hash:只分裂将要溢出的桶,使用目录项作为索引
- 多个目录项可能指向同一个桶
- 分裂时代价较小
- 翻倍目录项替代翻倍整个hash表
- 每次只分裂将要溢出桶
- 只需要进行局部重散列,重分布需要分裂的桶
- 目录指数级增长
- 数据分布不均时,会使得目录项很大
插入
D:全局位深度,hash值截断长度,为局部桶深度最大值L_i:桶局部深度,等于指向其目录项数目
若对应桶存在空闲位,则直接插入
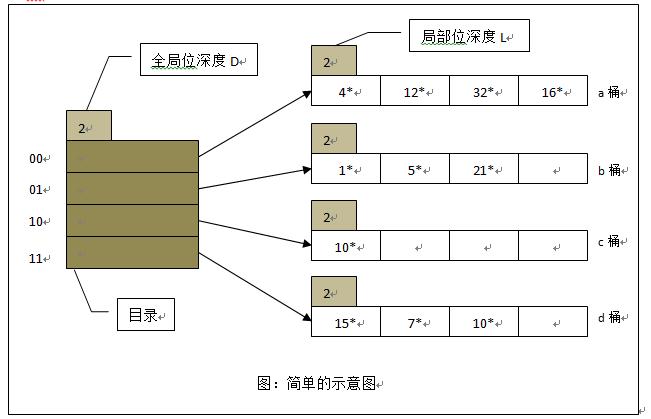
否则分裂桶:分裂后两桶局部深度加1
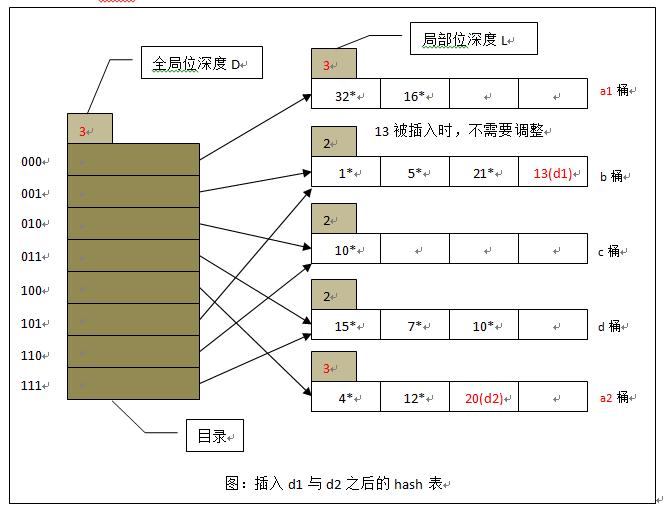
若分裂桶局部深度不大于全局位深度
- 创建新桶
- 重散列原始桶中数据
- 更新目录项中对应指针:分别指向分裂后桶
若分类桶局部深度大于全局位深度
- 更新全局位深度
- 目录项翻倍
- 创建新桶
- 重散列原始桶中数据
- 更新目录项中对应指针
- (新增)无关目录项仍然指向对应桶
- 相关目录项指向分别指向分裂后桶
查找
- 计算原始hash值
- 按照全局位深度截断
- 寻找相应目录项,找到对应桶,在桶中进行比较、查找
删除
- 计算原始hash值
- 按照全局位深度截断
- 寻找相应目录项,找到对应桶,在桶中进行比较、删除
- 若删除后发现桶为空,考虑与其兄弟桶合并,并使局部深度 减1
线性散列
线性散列:按次序分裂桶,保证整个建表过程类似完全二叉树
整个哈希表建表过程始终保持为完全二叉树
- 每次分裂的桶是完全二叉树编号最小的叶子节点
- 分裂前后桶间均为有序
相较于可扩展散列
- 无需存放数据桶指针的专门目录项,节省空间
- 能更自然的处理数据桶满的情况
- 允许更灵活的选择桶分裂时机
- 但若数据散列后分布不均,则问题可能比可扩散散列严重
实现相较而言更复杂
桶分裂
N:hash表中初始桶数目,应为2的幂次d = log_2N:表示桶数目需要位数level:分裂轮数,初始值为0,则每轮初始桶数为 $N * 2^{level}$Next:下次要发生分裂的桶编号
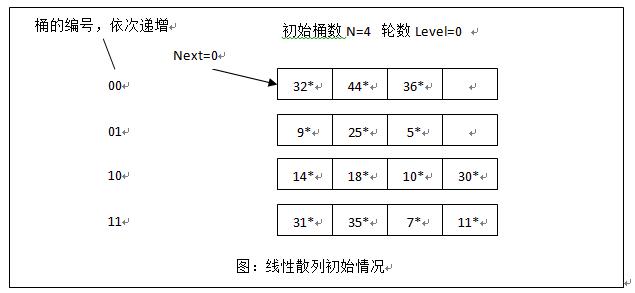
每次同分裂条件可以灵活选择
- 设置桶填充因子,桶中记录数达到该值时进行分裂
- 桶满时发生分裂
每次发生的分裂的桶总是由
Next决定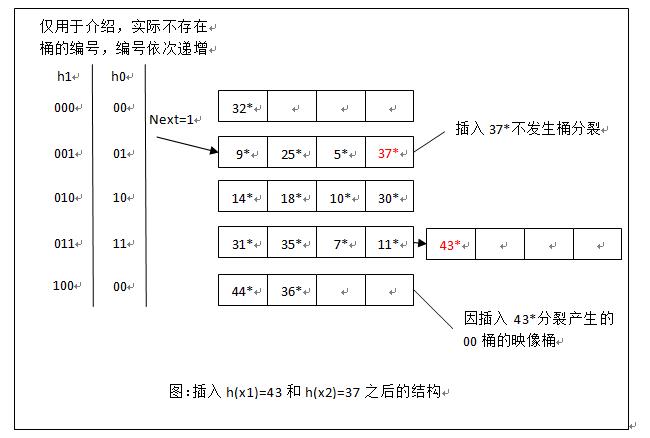
- 与当前被插入的桶溢出无关,可引入溢出页处理桶溢出
- 每次只分裂
Next指向的桶,桶分裂后Next += 1 - 后续产生映像桶总是位于上次产生映像桶之后
“轮转分裂进化”:各桶轮流进行分裂,一轮分裂完成后进入下轮 分裂
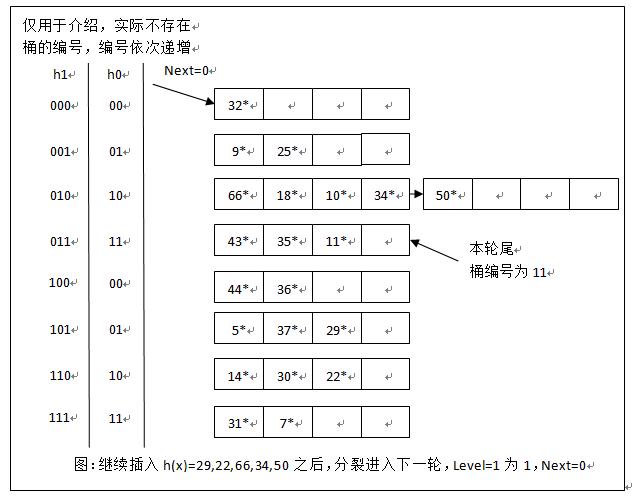
查找
根据
N、level计算当前d值,截取原始hash值若hash值位于
Next、N之间,说明该轮对应桶还未分裂, 直接在桶中查找若hash值小于
Next,说明该轮对应桶已经分裂,hash值向前 多取一位,在对应桶中查找
删除
- 删除操作是插入操作的逆操作
- 若删除元素后溢出块为空,可直接释放
- 若删除元素后某个桶元素为空,
Next -= 1- 当
Next减少到0,且最后桶也是空时,Next = N/2 - 1,同时level -= 1
- 当
1`

