Posted 2019-03-21Updated 2021-07-12Math Mixin / Time Series14 minutes read (About 2167 words)

Vector Auto-regression Model

VAR 模型：向量自回归模型

模型特点
- 不以经济理论为基础
- 结构简介明了
- 预测精度高
模型方程特点
- 采用多方程联立的形式
- 需要估计 $m(mp+1)$ 个参数的，对样本数量要求高
- 模型的每个方程中，内生变量 对模型的全部内生变量滞后项进行回归，估计全部内生变量的动态关系
模型用途
- 脉冲响应分析
- 方差分解

VAR 模型参数

VAR 模型系数由统计相关性估计
- 不具有逻辑上的因果关系
- 通常不直接解读 VAR 模型每个方程的经济学意义
VAR 模型参数不进行参数显著性检验，但是允许研究人员对参数施加特殊约束
VAR 模型通常是由一系列 非平稳序列构造的平稳系统
- 所以若包含非平稳变量，其中至少存在 1 个协整关系
- 协整关系具有经济学意义，可以解读系数（所以需要进行协整检验）

VAR模型形式

两变量 VAR(1)

方程组形式
$\begin{cases} & y_{1,t} = c_1 + \pi_{1,1}y_{1,t-1} + \pi_{1,2}y_{2,t-1} + u_{1t} \\ & y_{2,t} = c_2 + \pi_{2,1}y_{1,t-1} + \pi_{2,2}y_{2,t-1} + u_{2t} \\ \end{cases}$
矩阵形式
$\begin{bmatrix} y_{1,t} \\ y_{2,t} \end{bmatrix} = \begin{bmatrix} c_1 \\ c_2 \end{bmatrix} + \begin{bmatrix} \pi_{1,1} & \pi_{1,2} \\ \pi_{2,1} & \pi_{2,2} \\ \end{bmatrix} \begin{bmatrix} y_{1,t-1} \\ y_{2,t-1} \end{bmatrix} + \begin{bmatrix} u_{1,t} \\ u_{2,t} \end{bmatrix}$

$u{1,t}, u{2,t} \overset {i.i.d.} {\sim} (0, \theta^2)$：随机波动项，$Cov(u{1,t}, u{2,t}) = 0$

多变量的 VAR(k)（含外生变量）

$Y_t = C + \Pi_1 Y_{t-1} + \Pi_2 Y_{t-2} + \cdots + \Pi_k Y_{t-k} + U_t + \Phi Z_t$

$Yt = (y{1,t}, y{2,t}, \cdots, y{N,t})^T$：内生变量

$C = (c_1, c_2, \cdots, c_N)^T$：常数项
$\Pi_j = \begin{bmatrix}
  \pi_{11,j} & \pi_{12,j} & \cdots & \pi_{1N,j} \\
  \pi_{21,j} & \pi_{22,j} & \cdots & \pi_{2N,j} \\
  \vdots & \vdots & \ddots & \vdots \\
  \pi_{N1,j} & \pi_{N2,j} & \cdots & \pi_{NN,j} \\
\end{bmatrix}$：内生变量待估参数
$Ut = (u{1,t}, u{2,t}, \cdots, u{N,t})^T \overset {i.i.d.} {\sim} (0, \Omega)$：随机波动项

$Zt = (z{1,t}, z{2,t}, \cdots, z{N, t})^T$：外生变量

VAR(k) 变换

VAR(k) 模型可通过变换附加伴随矩阵式，改写为 VAR(1)

$\begin{align*} Y_t & = \Pi_1 Y_{t-1} + \Pi_2 Y_{t-2} + \cdots + \Pi_k Y_{t-k} + U_t \\ & = \begin{bmatrix} \Pi_1 & \Pi_2 & \cdots & \Pi_k \end{bmatrix} \begin{bmatrix} Y_{t-1} \\ Y_{t-2} \\ \vdots \\ Y_{t-k} \end{bmatrix} + U_t \\ & = AY + U_t \end{align*}$

Structured VAR

SVAR：结构 VAR 模型，在 VAR 模型基础上加入内生变量当期值

即解释变量中含有当期变量

两变量 SVAR(1)

$\begin{cases} & y_{1t} = c_1 + \pi_{11}y_{2t} + \pi_{12}y_{1,t-1} + \pi_{13}y_{1,t-2} + u_1 \\ & y_{2t} = c_2 + \pi_{21}y_{1t} + \pi_{22}y_{1,t-1} + \pi_{23}y_{1,t-2} + u_2 \\ \end{cases}$

含外生变量 VAR(1)

$\begin{align*} AY_t & = D + BY_{t-1} + FZ_t + V_t \\ Y_t & = A^{-1}D + A^{-1}BY_{t-1} + A^{-1}FZ_t + A^{-1}v_t \\ & = C + \Pi_1 Y_{t-1} + HZ_t + U_t \end{align*}$

$Y_t, Z_t, V_t$：内生变量向量、外生变量向量、误差项向量

$A, D, B, F$：模型结构参数

$C=A^{-1}D, \Pi_1=A^{-1}B, H=A^{-1}F, U_t=A^{-1}V_t$

VAR 模型稳定性

把脉冲施加在 VAR 模型中某个方程的 Iinnovation 过程上
- 随着时间推移，冲击会逐渐消失，则模型稳定
- 冲击不消失的则模型不稳定

一阶 VAR 模型分析

$\begin{align*} Y_t & = C + \Pi_1Y_{t-1} + U_t \\ & = (I + \Pi_1 + \Pi_1^2 + \cdots + \Pi_1^{t-1})C + \Pi_1^tY_0 + \sum_{i=0}^{t-1} \Pi_1^i U_{t-i} \end{align*}$

$\mu = (I + \Pi_1 + \Pi_2^2 + \cdots + \Pi_1^{t-1})C$：漂移向量

$Y_0$：初始向量

$U_t$：新息向量

$t \rightarrow \infty$ 时有
$I + \Pi_1 + \Pi_2^2 + \cdots + \Pi_1^{t-1} = (I-\Pi_1)^{-1}$

两变量 VAR(1) 稳定条件

$Y_t = C + \Pi_1 Y_{t-1} + U_t$

稳定条件
- 特征方程$|\Pi_1 - \lambda I|=0$根都在单位圆内
- 相反的特征方程$|I - L\Pi_1|=0$根都在单位圆外

VAR(k) 稳定条件

$\begin{align*} \begin{bmatrix} Y_t \\ Y_{t-1} \\ Y_{t-2} \\ \vdots \\ Y_{t-k+1} \end{bmatrix} & = \begin{bmatrix} C \\ 0 \\0 \\ \vdots \\ 0 \end{bmatrix} + \begin{bmatrix} \Pi_1 & \Pi_2 & \cdots & \Pi_{k-1} & \Pi_{k} \\ I & 0 & \cdots & 0 & 0 \\ 0 & I & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & I & 0 \end{bmatrix} \begin{bmatrix} Y_{t-1} \\ Y_{t-2} \\ Y_{t-3} \\ \vdots \\ Y_{t-k} \end{bmatrix} + \begin{bmatrix} U_t \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \\ & = [C|0]^T + AY + U \end{align*}$

$A$：$Nk$ 阶方阵

$N$：回归向量维度

$k$：自回归阶数

稳定条件
- 特征方程 $|A - \lambda I| = 0$ 根全在单位圆内
- 相反的特征方程 $|I - LA| = 0$ 根全在单位圆外

VEC 模型

N 变量 VEC(k)

$\begin{align*} \Delta Y_t & = y_{t-1} + \Pi Y_{t-1} + \Gamma_1 \Delta Y_{t-2} + \cdots + \Gamma_{k-1} \Delta Y_{t-p+1} + U_t + \Phi Z_t \end{align*}$

$\Pi = \sum_{i=1}^k \Pi_i - I$：影响矩阵

$\Gammai = -\sum{j=i+1}^k$

VEC(1)

$\begin{align*} \Delta Y_{t} & = \Pi Y_{t-1} + \Gamma \Delta Y_{t-1} \\ & = \alpha \beta^{'} Y_{t-1} + \Gamma \Delta Y_{t-1} \\ & = \alpha ECM_{t-1} + \Gamma \Delta Y_{t-1} \end{align*}$

Impulse-Response Function

脉冲响应函数：描述内生变量对误差冲击的反应

脉冲响应函数含义
- 在随机误差下上施加标准查大小的冲击后，对内生变量当期值和未来值所带来的影响
- 即将 VAR 模型表示为无限阶的向量 $MA(\infty)$ 过程
对脉冲响应函数的解释的困难源于，实际中各方程对应误差项不是完全非相关
- 误差相关时，其有一个共同组成部分，不能被任何特定变量识别
- 故，左乘变换矩阵 $M$ 得到 $V_t = MU_t$ 修正相关性（常用 Cholesky 分解求解）
  - 即将其协方差矩阵变换为对角矩阵 $V_t = MU_t \sim (0, \Omega)$

VAR(1) 转换为 MA

$\begin{align*} Y_t & = AY_{t-1} + U_t \\ (I - LA)Y_t & = U_t \\ Y_t & = (I-LA)^{-1} U_t \\ & = U_t + AU_{t-1} + A^2U_{t-2} + \cdots + A^sU_t + \cdots\\ Y_{t+s} & = U_{t+s} + \Psi_1U_{t+s-1} + \Psi_2U_{t+s-2} + \cdots + \Psi_sU_t + \cdots \end{align*}$

$\Psis = A^s = \frac {\partial Y{t+s}} {\partial U_t}$

$\Psis[i, j] = \frac {\partial y{i,t+s}} {\partial u{j,t}}$：脉冲响应函数，表示其他误差项在任何时期都不变条件下，第 $j$ 个变量 $y{j,t}$ 在对应误差项 $u{j,t}$ 在 $t$ 期受到一个单位冲击后，对第 $i$ 个内生变量 $y{i,t}$ 在 $t+s$ 期造成的影响

方差分解

方差分解：分析未来 $t+s$ 期 $y_{j, t+s}$ 的预测误差受不同新息冲击影响比例

均方误差

误差可以写为 MA 形式
$Y_{t+s} - \hat Y_{t+s|t} = U_{t+s} + \Psi_1U_{t+s-1} + \Psi_2U_{t+s-2} + \cdots + \Psi_{s-1}U_{t+1}$
则预测s期的均方误差为
$\begin{align*} MSE(\hat Y_{t+s|t}) & = E[(Y_{t+s} - \hat Y_{t+s|t}) (Y_{t+s} - \hat Y_{t+s|t})^T] \\ & = \Omega + \Psi_1\Omega\Psi_1^T + \cdots + \Psi_{s-1}\Omega\Psi_{s-1}^T \end{align*}$

$\Omega = E(U_tU_t^T)$：不同期 $U_t$ 协方差阵为 0

计算比例

$\begin{align*} U_t &= MV_t \\ &= m_1v_{1,t} + m_2v_{2,t} + \cdots + m_Nv_{N,t} \\ \Omega & = E(U_t, U_t^T) \\ & = (MV_t)(MV_t)^T \\ & = m_1m_1^TVar(v_{1,t} + \cdots + m_Nm_N^TVar(v_{N,t}) \end{align*}$

$v{1,t}, v{2,t}, \cdots, v_{N,t}$不相关

将 $\Omega$ 带入 MSE 表达式中，既可以得到第 $j$ 个新息对 $s$ 期预测量 $\hat Y_{t+s|t}$ 的方差贡献比例

VAR 建模

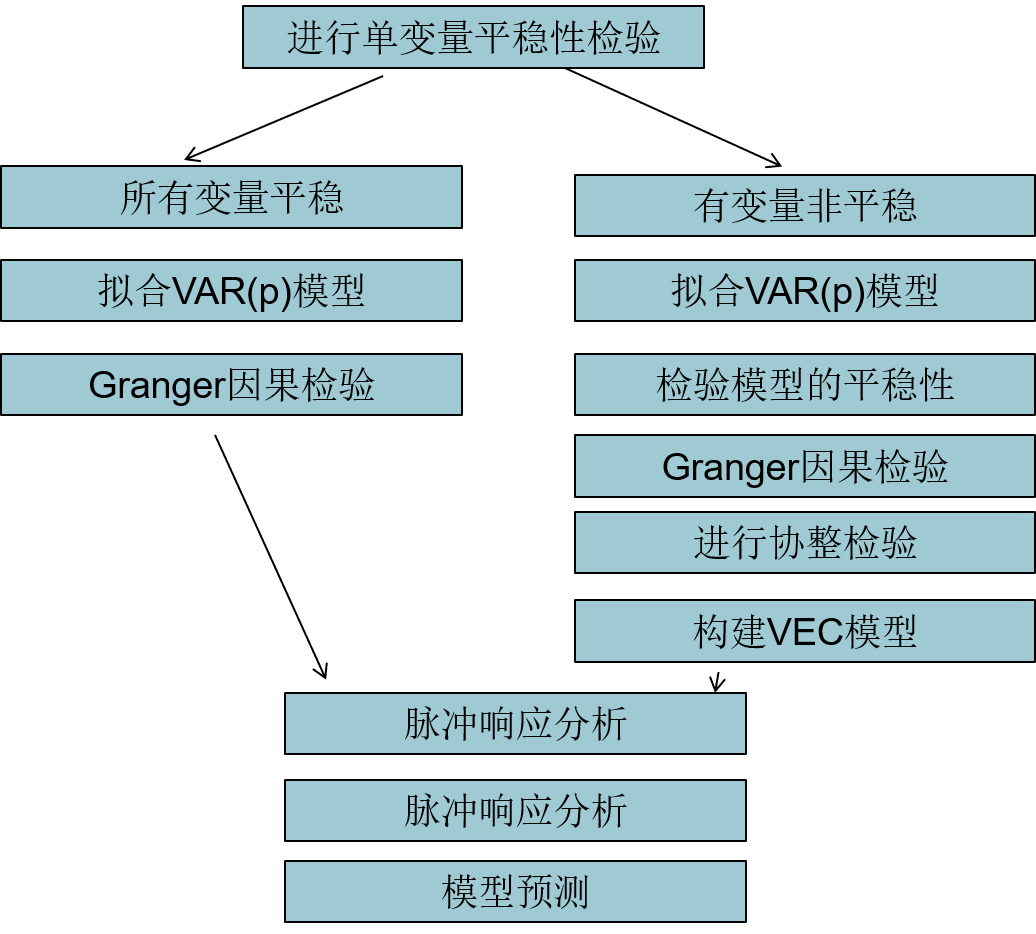
var_procedure

进行单变量平稳性检验
拟合 VAR(p) 模型
- 确定模型阶数
  - 理论上初步模型阶数可以任意确定
  - 然后根据 AIC、BIC、对数似然函数值选择相对最优阶数
若所有变量平稳，则 Granger 因果检验
- VAR 模型通过平稳性检验，理论上就可以利用模型进行分析、预测
- 但 VAR 模型是超系数模型，默认所有内生变量互为因果
  - 但实际上变量之间因果关系复杂
  - 可通过 Granger 因果检验判断变量之间长期、短期因果关系
若有变量非平稳
- 检验模型平稳性
- Granger 因果检验
- 协整检验：JJ 检验
  - 非平稳系统必然存在协整关系，具有经济学意义
  - 所以需要找出存在的基础协整关系，解读其代表的长期、短期相关影响
- 构建 VEC 模型
  - 如果协整检验显示基本协整关系满秩，说明系统中每个序列都是平稳序列，直接建立VAR模型
  - 如果协整检验限制基本协整关系为 0 秩，则系统不存在协整关系，通常说明系统不平稳，需要重新选择变量，或者适当差分后建模
  - 最常见情况是协整检验显示基本协整关系数量处于 0 至满秩中间，此时建立 $VEC$ 模型
脉冲响应分析
方差分析
模型预测

Vector Auto-regression Model