Posted Updated Math Mixina few seconds read (About 40 words)

常用等式

常用定理

Lucas 定理

  • $p < 10^5$：必须为素数

Holder 定理

$|x|^{*}_p = |x|_q$

  • $\frac 1 p + \frac 1 q = 1$
Posted Updated Math Mixin2 minutes read (About 252 words)

未归类概念

Radial Basis Function

  • RBF 径向基函数：取值仅依赖到原点距离的实值函数，即 $\phi(x) = \phi(|x|)$

    • 也可以按照距离某中心点 $c$ 的距离定义，即 $\phi(x) = \phi(|x-c|)$
    • 其中距离一般为使用 $L_2$ 范数，即欧式距离
    • 函数 $\phi$ 一般与 $|x|$ 负相关

  • 径向基函数最初用于解决多变量插值问题

    • 即以各样本为中心创建多个径向基函数
    • 多个径向基函数加权加和即得到拟合的函数曲线，可用于函数插值

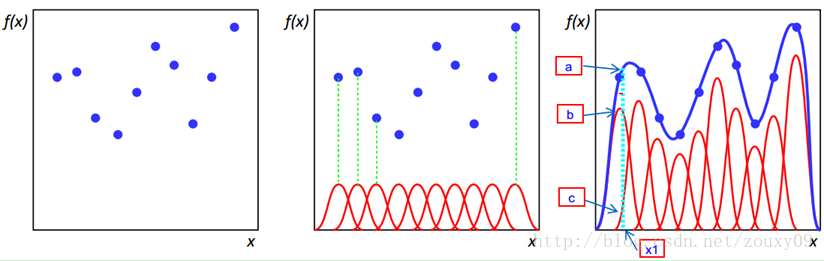
    rbf_for_interpolation

常见径向基函数

  • 定义 $r=|x-x_i|$

  • 高斯函数

  • Multiquadric 多二次函数：

  • Inverse Quadric 逆二次函数：

  • Polyharmonic Spline 多重调和样条：

  • Thin Plate Spline 薄板样条（多重调和样条特例）：

Posted Updated Math Mixin9 minutes read (About 1338 words)

距离函数

距离

  • 距离可认为是两个对象 $x,y$ 之间的 相似程度
    • 距离和相似度是互补的
    • 可以根据处理问题的情况，自定义距离

Bregman Divergence

  • $Phi(x)$：凸函数

  • 布雷格曼散度：穷尽所有关于“正常距离”的定义

    • 给定 $R^n * R^n \rightarrow R$ 上的正常距离 $D(x,y)$，一定可以表示成布雷格曼散度形式
    • 直观上：$x$处函数、函数过$y$点切线（线性近似）之差
      • 可以视为是损失、失真函数：$x$由$y$失真、近似、添加噪声得到

  • 特点

    • 非对称：$D(x, y) = D(y, x)$
    • 不满足三角不等式：$D(x, z) \leq D(x, y) + D(y, z)$
    • 对凸集作 Bregman Projection 唯一
      • 即寻找凸集中与给定点Bregman散度最小点
      • 一般的投影指欧式距离最小
Domain $\Phi(x)$ $D_{\Phi}(x,y)$ Divergence
$R$ $x^2$ $(x-y)^2$ Squared Loss
$R_{+}$ $xlogx$ $xlog(\frac x y) - (x-y)$
$[0,1]$ $xlogx + (1-x)log(1-x)$ $xlog(\frac x y) + (1-x)log(\frac {1-x} {1-y})$ Logistic Loss
$R_{++}$ $-logx$ $\frac x y - log(\frac x y) - 1$ Itakura-Saito Distance
$R$ $e^x$ $e^x - e^y - (x-y)e^y$
$R^d$ $\ x\ $ $\ x-y\ $ Squared Euclidean Distance
$R^d$ $x^TAx$ $(x-y)^T A (x-y)$ Mahalanobis Distance
d-Simplex $\sum_{j=1}^d x_j log_2 x_j$ $\sum_{j=1}^d x_j log_2 log(\frac {x_j} {y_j})$ KL-divergence
$R_{+}^d$ $\sum_{j=1}^d x_j log x_j$ $\sum{j=1}^d x_j log(\frac {x_j} {y_j}) - \sum{j=1}^d (x_j - y_j)$ Genelized I-divergence
  • 正常距离：对满足任意概率分布的点，点平均值点（期望点）应该是空间中距离所有点平均距离最小的点
  • 布雷格曼散度对一般概率分布均成立，而其本身限定由凸函数生成
    • 和 Jensen 不等式有关？凸函数隐含部分对期望的度量
  • http://www.jmlr.org/papers/volume6/banerjee05b/banerjee05b.pdf

单点距离

Minkowski Distance

闵科夫斯基距离：向量空间 $\mathcal{L_p}$ 范数

  • 表示一组距离族

    • $p=1$：Manhattan Distance，曼哈顿距离
    • $p=2$：Euclidean Distance，欧式距离
    • $p \rightarrow \infty$：Chebychev Distance，切比雪夫距离

  • 闵氏距离缺陷

    • 将各个分量量纲视作相同
    • 未考虑各个分量的分布

Mahalanobis Distance

马氏距离：表示数据的协方差距离

  • $\Sigma$：总体协方差矩阵
  • 优点
    • 马氏距离和原始数据量纲无关
    • 考虑变量相关性
  • 缺点
    • 需要知道总体协方差矩阵，使用样本估计效果不好

LW Distance

兰氏距离：Lance and Williams Distance，堪培拉距离

  • 特点
    • 对接近0的值非常敏感
    • 对量纲不敏感
    • 未考虑变量直接相关性，认为变量之间相互独立

Hamming Distance

汉明距离：差别

  • $v_i \in {0, 1}$：虚拟变量
  • $p$：虚拟变量数量
  • 可以衡量定性变量之间的距离

Embedding

  • 找到所有点、所有维度坐标值中最大值 $C$
  • 对每个点 $P=(x_1, x_2, \cdots, x_d)$
    • 将每维 $x_i$ 转换为长度为 $C$ 的 0、1 序列
    • 其中前 $x_i$ 个值为 1，之后为 0
  • 将 $d$ 个长度为 $C$ 的序列连接，形成长度为 $d * C$ 的序列
  • 以上汉明距离空间嵌入对曼哈顿距离是保距的

Jaccard 系数

Jaccard 系数：度量两个集合的相似度，值越大相似度越高

  • $S_1, S_2$：待度量相似度的两个集合

Consine Similarity

余弦相似度

  • $x_1, x_2$：向量

欧式距离

点到平面

  • $T={(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$：样本点集
  • $wx + b = 0$：超平面
Functional Margin 函数间隔

  • 函数间隔可以表示分类的正确性、确信度

    • 正值表示正确
    • 间隔越大确信度越高

  • 点集与超平面的函数间隔取点间隔最小值 $\hat{T} = \min_{i=1,2,\cdots,n} \hat{\gamma_i}$

  • 超平面参数 $w, b$ 成比例改变时，平面未变化，但是函数间隔成比例变化

Geometric Margin 几何间隔

  • 几何间隔一般是样本点到超平面的 signed distance

    • 点正确分类时，几何间隔就是点到直线的距离

  • 几何间隔相当于使用 $|w|$ 对函数间隔作规范化

    • $|w|=1$ 时，两者相等
    • 几何间隔对确定超平面、样本点是确定的，不会因为超平面表示形式改变而改变

  • 点集与超平面的几何间隔取点间隔最小值 $\hat{T} = \min_{i=1,2,\cdots,n} \hat{\gamma_i}$

Levenshtein/Edit Distance

（字符串）编辑距离：两个字符串转换需要进行插入、删除、替换操作的次数

组间距离

Single Linkage

Average Linkage

Complete Linkage

Posted Updated Math Mixin27 minutes read (About 4010 words)

Hashing

Hash Function

  • hash：散列/哈希，将任意类型值转换为关键码值
  • hash function：哈希/散列函数，从任何数据中创建小的数字“指纹”的方法
  • hash value：哈希值，哈希函数产生关键码值
  • collision：冲突，不同两个数据得到相同哈希值
  • 哈希函数应该尽可能使得哈希值均匀分布在目标空间中
    • 降维：将高维数据映射到低维空间
    • 数据应该低维空间中尽量均匀分布

数据相关性

  • Data Independent Hashing：数据无关哈希，无监督，哈希函数基于某种概率理论

    • 对原始的特征空间作均匀划分
    • 对分布不均、有趋向性的数据集时，可能会导致高密度区域哈希桶臃肿，降低索引效率

  • Data Dependent Hashing：数据依赖哈希，有监督，通过学习数据集的分布从而给出较好划分的哈希函数

    • 得到针对数据密度动态划分的哈希索引
    • 破坏了传统哈希函数的数据无关性，索引不具备普适性

应用

  • 查找数据结构：cs_algorithm/data_structure/hash_table
    • 哈希表
  • 信息安全方向：cs_algorithm/specification/info_security
    • 文件检验
    • 数字签名
    • 鉴权协议

哈希函数

  • 简单哈希函数主要用于提升查找效率（构建哈希表）

    • 要求哈希函数的降维、缩小查找空间性质
    • 计算简单、效率高

  • 复杂哈希函数主要用于信息提取

    • 要求哈希函数的信息提取不可逆、非单调映射
    • 查表哈希
      • CRC 系列算法：本身不是查表，但查表是其最快实现
      • Zobrist Hashing
    • 混合哈希：利用以上各种方式
      • MD5
      • Tiger

单值输入

  • 直接寻址法：取关键字、或其某个线性函数值 $hash(key) = (a * key + b) \% prime$

    • $prime$：一般为质数，以使哈希值尽量均匀分布，常用的如：$2^{32}-5$

  • 数字分析法：寻找、利用数据规律构造冲突几率较小者

    • 如：生日信息前 2、3 位大体相同，冲突概率较大，优先舍去

  • 平方取中法：取关键字平方后中间几位

  • 折叠法：将关键字分割为位数相同部分，取其叠加和

  • 随机数法：以关键字作为随机数种子生成随机值

    • 适合关键字长度不同场合
  • 常用于之前哈希结果再次映射为更小范围的最终哈希值

序列输入

加法哈希

加法哈希：将输入元素相加得到哈希值

  • 标准加法哈希

    1
    2
    3
    4
    5
    6
    AddingHash(input):
    	hash = 0
    	for ele in input:
    		hash += ele
    	# prime 为任意质数，常用 2^32 - 5
    	hash = hash  % prime
    • 最终哈希结果 $\in [0, prime-1]$

位运算哈希

位运算哈希：利用位运算（移位、异或等）充分混合输入元素

  • 标准旋转哈希

    1
    2
    3
    4
    5
    RotationHash(input):
    	hash = 0
    	for ele in input:
    		hash = (hash << 4) ^ (hash >> 28) ^ ele
    	return hash % prime

  • 变形 1

    1
    hash = (hash<< 5) ^ (hash >> 27) ^ ele

  • 变形2

    1
    2
    3
    hash += ele
    hash ^= (hash << 10)
    hash ^= (hash >> 6)

  • 变形3

    1
    2
    3
    4
    if (ele & 1) == 0:
    	hash ^= (hash << 7) ^ ele ^ (hash >> 3)
    else:
    	hash ^= ~((hash << 11) ^ ele ^ (hash >> 5))

  • 变形4

    1
    hash += (hash << 5) + ele

  • 变形5

    1
    hash = ele + (hash << 6) + (hash >> 16) - hash

  • 变形6

    1
    hash ^= (hash << 5) + ele + (hash >> 2)

乘法哈希

乘法哈希：利用乘法的不相关性

  • 平方取头尾随机数生成法：效果不好

  • Bernstein 算法

    1
    2
    3
    4
    5
    Bernstein(input):
    	hash = 0
    	for ele in input:
    		hash = 33 * hash + ele
    	return hash
    • 其他常用乘数：31、131、1313、13131、131313

  • 32位 FNV 算法

    1
    2
    3
    4
    5
    6
    7
    M_SHIFT =
    M_MASK =
    FNVHash(input):
    	hash = 2166136261;
    	for ele in input:
    		hash = (hash * 16777619) ^ ele
    	return (hash ^ (hash >> M_SHIFT)) & M_MASK

  • 改进的 FNV 算法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    FNVHash_2(input):
    	hash = 2166136261;
    	for ele in input:
    		hash = (hash ^ ele) * 16777619
    	hash += hash << 13
    	hash ^= hash >> 7
    	hash += hash << 3
    	hash ^= hash >> 17
    	hash += hash << 5
    	return hash

  • 乘数不固定

    1
    2
    3
    4
    5
    6
    7
    RSHash(input):
    	hash = 0
    	a, b = 378551, 63689
    	for ele in input:
    		hash = hash * a + ele
    		a *= b
    	return hash & 0x7FFFFFFF
  • 除法也类似乘法具有不相关性，但太慢

定长序列

  • 两步随机数

    1
    2
    3
    4
    5
    6
    main_rand_seq = randint(k)
    TwoHashing(input[0,...,k]):
    	hash = 0
    	from i=0 to k:
    		hash += input[i] * main_rand_seq[i]
    	hash = hash mod prime

Universal Hashing

  • 全域哈希：键集合 $U$ 包含 $n$ 个键、哈希函数族 $H$ 中哈希函数 $h_i: U \rightarrow 0..m$，若 $H$ 满足以下则为全域哈希 $$
      \forall x \neq y \in U, | \{h|h \in H, h(x) = h(y) \} | = \frac {|H|} m
    $$
    • $|H|$：哈希函数集合 $H$ 中函数数量
  • 独立与键值随机从中选择哈希函数，避免发生最差情况
  • 可利用全域哈希构建完美哈希

性质

  • 全域哈希 $H$ 中任选哈希函数 $h_i$，对任意键 $x \neq y \in U$ 冲突概率小于 $\frac 1 m$

    • 由全域哈希函数定义，显然

  • 全域哈希 $H$ 中任选哈希函数 $hi$，对任意键 $x \in U$，与其冲突键数目期望为 $\frac n m$，即 $E{[collision_x]}=\frac n m$

    • $C_x$：任选哈希函数，与 $x$ 冲突的键数量
    • $C_{xy} = \left { \begin{matrix} 1, & h_i(x) = h_i(y) \ 0, & otherwise \end{matrix} \right.$：指示 $x,y$ 是否冲突的指示变量
    • $m = n^2$ 时，冲突期望小于 0.5
      • $n$ 个键两两组合数目为 $C_n^2$
      • 则 $E_{total} < C_n^2 \frac 1 n < 0.5$

例

  • 以下构造 $[0,p-1] \rightarrow [0,m-1]$ 全域哈希

  • $p$ 为足够大素数使得所有键值 $\in [0,p-1]$

    • 记 $Z_p = { 0,1,\cdots,p-1 }$
    • 记 $Z_p^{*}={ 1,2,\cdots,p-1 }$
    • 且哈希函数映射上限（哈希表长度） $m < max(U) < p$

  • 记哈希函数

  • 则以下哈希函数族即为全域哈希

Locality Sensitive Hashing

LSH：局部敏感哈希

  • $(r_1,r_2,P_1,P_2)-sensitive$ 哈希函数族 $H$ 需满足如下条件 $$ \begin{align*}
      Pr_{H}[h(v) = h(q)] \geq P_1, & \forall q \in B(v, r_1) \\
  Pr_{H}[h(v) = h(q)] \geq P_2, & \forall q \notin B(v, r_2) \\
    \end{align*}$$
    • $h \in H$
    • $r_1 < r_2, P_1 > P_2$：函数族有效的条件
    • $B(v, r)$：点 $v$ 的 $r$ 邻域
    • $r_1, r_2$：距离，强调比例时会表示为 $r_1 = R, r_2 = cR$
  • 此时 相似目标（距离小）有更大概率发生冲突

LSH查找

思想

general_lsh_comparsion

  • 相似目标更有可能映射到相同哈希桶中

    • 则只需要在目标所属的哈希桶中进行比较、查找即可
    • 无需和全集数据比较，大大缩小查找空间

  • 可视为降维查找方法

    • 将高维空间数据映射到 1 维空间，寻找可能近邻的数据点
    • 缩小范围后再进行精确比较

概率放大

  • 期望放大局部敏感哈希函数族 $Pr_1, Pr_2$ 之间差距

  • 增加哈希值长度（级联哈希函数中基本哈希函数数量） $k$

    • 每个哈希函数独立选择，则对每个级联哈希函数 $g_i$ 有 $Pr[g_i(v) = g_i(q)] \geq P_1^k$
    • 虽然增加哈希键位长会减小目标和近邻碰撞的概率，但同时也更大程度上减少了和非近邻碰撞的概率、减少搜索空间
    • 级联哈希函数返回向量，需要对其再做哈希映射为标量，方便查找

  • 增加级联哈希函数数量（哈希表数量） $L$

    • $L$个哈希表中候选项包含真实近邻概率 至少 为 $1 - (1 - P_1^k)^L$
    • 增加哈希表数量能有效增加候选集包含近邻可能性
    • 但同时也会增大搜索空间

搜索近似最近邻

  • 使用 $L$ 个级联哈希函数分别处理待搜索目标
  • 在 $L$ 个哈希表分别寻找落入相同哈希桶个体作为候选项
  • 在所有候选项中线性搜索近邻

基于汉明距离的 LSH

  • 在汉明距离空间中搜索近邻
    • 要求数据为二进制表示
    • 其他距离需要嵌入汉明距离空间才能使用
      • 欧几里得距离没有直接嵌入汉明空间的方法
        • 一般假设欧几里得距离和曼哈顿距离差别不大
        • 直接使用对曼哈顿距离保距嵌入方式

设计哈希函数族

  • 考虑哈希函数族 $H = { h_1, h_2, \cdots, h_m }$

    • 其中函数 $h_i$ 为 ${0, 1}^d$ 到 ${0, 1}$ 的映射：随机返回特定比特位上的值

  • 从 $H$ 中随机的选择哈希函数 $h_i$

    • 则 $Pr[h_i(v) = h_i(q)]$ 等于 $v, q$ 相同比特数比例，则
      • $Pr_1 = 1 - \frac R d$
      • $Pr_2 = 1 - \frac {cR} d$
    • 考虑到 $Pr_1 > Pr_2$，即此哈希函数族是局部敏感的

基于 Jaccard 系数的 LSH

  • 考虑 $M * N$ 矩阵 $A$，元素为 0、1

    • 其中
      • $M$：集合元素数量
      • $N$：需要比较的集合数量
    • 目标：寻找相似集合，即矩阵中相似列

  • 用 Jaccard 系数代表集合间相似距离，用于搜索近邻

    • 要求各数据向量元素仅包含 0、1：表示集合是否包含该元素

定义 Min-hashing 函数族

  • 对矩阵 $A$ 进行 行随机重排 $\pi$，定义 Min-hashing 如下

    • $C$：列，表示带比较集合
    • $\min \pi(C)$：$\pi$ 重排矩阵中 $C$ 列中首个 1 所在行数

  • 则不同列（集合） Min-hashing 相等概率等于二者 Jaccard 系数

    • $a$：列 $C_1, C_2$ 取值均为 1 的行数
    • $b$：列 $C_1, C_2$ 中仅有一者取值为 1 的行数
    • 根据 Min-hashing 定义，不同列均取 0 行被忽略

Min-hashing 实现

  • 数据量过大时，对行随机重排仍然非常耗时，考虑使用哈希函数模拟行随机重排

    • 每个哈希函数对应一次随机重排
      • 哈希函数视为线性变换
      • 然后用哈希函数结果对总行数取模
    • 原行号经过哈希函数映射即为新行号

  • 为减少遍历数据次数，考虑使用迭代方法求解

    1
    2
    3
    4
    5
    6
    for i from 0 to N-1:
    	for j from 0 to M-1:
    		if D[i][j] == 1:
    			for k from 1 to K:
    				# 更新随机重拍后，第 `j` 列首个 1 位置
    				DD[k][j] = min(h_k(i), DD[k][j])
    • $D$：原始数据特征矩阵
    • $DD$：$Min-hashing* 签名矩阵
    • $N$：特征数量，原始特征矩阵行数
    • $M$：集合数量，原始特征矩阵列数
    • $K$：模拟的随机重排次数，Min-hashing 签名矩阵行数
    • $h_k,k=1,…,K$：$K$ 个模拟随机重排的哈希函数，如 $h(x) = (2x + 7) mod N$
    • 初始化 Min-hashing 签名矩阵所有值为 $\infty$
    • 遍历 $N$ 个特征、$M$ 个集合
      • 查看每个对应元素是否为 1
      • 若元素为 1，则分别使用 $K$ 个哈希函数计算模拟重排后对应的行数
      • 若计算出行数小于当前 *Min-hash$ 签名矩阵相应哈希函数、集合对应行数，更新
    • 遍历一遍原始数据之后即得到所有模拟重排的签名矩阵

Exact Euclidean LSH

  • $E^2LSH$：欧式局部LSH，LSH Based-on P-stable Distribution

    • 使用内积将向量随机映射到哈希值
    • p-stable 分布性质将欧式距离同哈希值相联系，实现局部敏感

  • $E^2LSH$ 特点

    • 基于概率模型生成索引编码结果不稳定
    • 随编码位数 $k$ 增加的，准确率提升缓慢
    • 级联哈希函数数量 $L$ 较多时，需要大量存储空间，不适合大规模数据索引

p-stable 哈希函数族

  • $v$：$n$ 维特征向量
  • $a = (X_1,X_2,\cdots,X_n)$：其中分量为独立同 p-stable 分布的随机变量
  • $b \in [0, r]$：均匀分布随机变量

p-stable 哈希函数碰撞概率

  • 考虑$|v_1 - v_2|_p = c$的两个样本碰撞概率

  • 显然，仅在 $|av1 - av_2| \leq r$ 时，才存在合适的 $b$ 使得 $h{a,b}(v1) = h{a,b}(v_2)$

    • 即两个样本碰撞，不失一般性可设 $av_1 \leq av_2$
    • 此 $r$ 即代表局部敏感的 局部范围

  • 若 $(k-1)r \leq av_1 \leq av_2 < kr$，即两个样本与 $a$ 内积在同一分段内

    • 易得满足条件的 $b \in [0,kr-av_2) \cup [kr-av_1, r]$
    • 即随机变量 $b$ 取值合适的概率为 $1 - \frac {av_2 - av_1} r$

  • 若 $(k-1)r \leq av_1 \leq kr \leq av_2$，即两个样本 $a$ 在相邻分段内

    • 易得满足条件的 $b \in [kr-av_1, (k+1)r-av_2)$
    • 即随机变量 $b$ 取值合适的概率同样为 $1 - \frac {av_2 - av_1} r$

  • 考虑 $av_2 - av_1$ 分布为 $cX$，则两样本碰撞概率为

    • $c = |v_1 - v_2|_p$：特征向量之间$L_p$范数距离
    • $t = a(v_1 - v_2)$
    • $f$：p稳定分布的概率密度函数

    • $p=1$ 柯西分布

    • $p=2$ 正态分布

性质、实现

限制近邻碰撞概率

  • $r$ 最优值取决于数据集、查询点

    • 根据文献，建议$r = 4$

  • 若要求近邻 $v \in B(q,R)$以不小于$1-\sigma$ 概率碰撞，则有

    则可取

  • $k$ 最优值是使得 $T_g + T_c$ 最小者

    • $T_g = O(dkL)$：建表时间复杂度
    • $T_c = O(d |collisions|)$：精确搜索时间复杂度
    • $T_g$、$T_c$ 随着 $k$ 增大而增大、减小
限制搜索空间

  • 哈希表数量 $L$ 较多时，所有碰撞样本数量可能非常大，考虑只选择 $3L$ 个样本点

  • 此时每个哈希键位长 $k$、哈希表数量 $L$ 保证以下条件，则算法正确

    • 若存在 $v^{ }$ 距离待检索点 $q$ 距离小于 $r_1$，则存在 $g_j(v^{ }) = g_j(q)$

    • 与 $q$ 距离大于 $r_2$、可能和 $q$ 碰撞的点的数量小于 $3L$

  • 可以证明，$k, L$ 取以下值时，以上两个条件以常数概率成立 （此性质是局部敏感函数性质，不要求是 $E^2LSH$）

  • $\rho$ 对算法效率起决定性作用，且有以下定理

    • 距离尺度 $D$ 下，若 $H$ 为 $(R,cR,p1,p_2)$-敏感哈希函数族，则存在适合 (R,c)-NN 的算法，其空间复杂度为 $O(dn + n^{1+\rho})$、查询时间为 $O(n^{\rho})$ 倍距离计算、哈希函数计算为 $O(n^{\rho} log{1/p_2}n)$， 其中 $\rho = \frac {ln 1/p_1} {ln 1/p_2}$
    • $r$ 足够大、充分远离 0 时，$\rho$ 对其不是很敏感
    • $p1, p_2$ 随 $r$ 增大而增大，而 $k = log{1/p_2} n$ 也随之增大，所以 $r$ 不能取过大值

Scalable LSH

Scalable LSH：可扩展的 LSH

  • 对动态变化的数据集，固定哈希编码的局部敏感哈希方法对数据 动态支持性有限，无法很好的适应数据集动态变化

    • 受限于初始数据集分布特性，无法持续保证有效性
    • 虽然在原理上支持数据集动态变化，但若数据集大小发生较大变化，则其相应哈希参数（如哈希编码长度）等需要随之调整，需要从新索引整个数据库

  • 在 $E^2LSH$ 基础上通过 动态增强哈希键长，增强哈希函数区分能力，实现可扩展 LSH

Posted Updated ML Theory / Optimization8 minutes read (About 1136 words)

Robust Optimization

背景

稳健优化：利用凸理论、对偶理论中概念，使得凸优化问题中的解 对参数的bounded uncertainty有限不确定性（波动）不敏感

  • 稳健优化在机器学习涉及方面：不确定优化、过拟合

    • Connecting Consistency
    • Generalization Ability
    • Sparsity
    • Stability

  • 不确定性来源

    • 模型选择错误
    • 假设不成立
    • 忽略必要因素
    • 经验分布、函数无法正确估计整体分布

  • 过拟合判断依据

    • metric entropy
    • VC-dimension

对比

优化问题对问题参数的扰动非常敏感，以至于解经常不可行、次优

  • Stochastic Programming：使用概率描述参数不确定性，

  • 稳健优化则假设问题参数在某个给定的先验范围内随意变动

    • 不考虑参数的分布

    • 利用概率论的理论，而不用付出计算上的代价

策略（最优化问题）

  • $\mathcal{U}_i $：uncertainty set，不确定集

Computational Tractablity

稳健优化易解性：在满足标准或一点违反 Slater-like regularity conditions情况下，求解稳健优化问题 等同于求解对以下凸集$\mathcal{X(U)}$的划分（求出凸集）

  • 若存在高效算法能确定$x \in \mathcal{X(U)}$、或者能够提供 分离超平面，那么问题可以在多项式时间中求解

  • 即使所有的约束函数$f_i$都是凸函数，此时$\mathcal{X(U)}$ 也是凸集，也有可能没有高效算法能够划分出$\mathcal{X(U)}$

  • 然而在大部分情况下，稳健化后的问题都能高效求解下，和原 问题复杂度相当

复杂度说明

  • LP + Polyhedra Uncertainty：LP
  • LP + Ellipsoidal Uncertainty：SOCP
  • CQP + Ellipsoidal Uncertainty：SDP
  • SDP + Ellipsoodal Uncertainty：NP-hard
  • LP：Linear Program，线性规划
  • SOCP：Second-Order Cone Program，二阶锥规划
  • CQP：Convex Quadratic Program，凸二次规划
  • SDP：Semidefinite Program，半定规划
  • Polyhedra Uncertainty：多项式类型不确定
  • Ellipsodial Uncertainty：椭圆类型不确定
  • NP-hard：NP难问题，至少和NPC问题一样困难得问题

Example

Linear Programs with Polyhedral Uncertainty

概率解释、结果

  • 稳健优化的计算优势很大程度上来源于，其形式是固定的，不再 需要考虑概率分布，只需要考虑不确定集

  • 计算优势使得，即使不确定性是随机、且分布已知，稳健优化 仍然具有吸引力

  • 在一些概率假定下，稳健优化可以给出稳健化问题解的某些 概率保证，如：可行性保证（在给定约束下，解能以多大概率 不超过约束）

Uncertainty Set

Atomic Uncertainty Set

原子不确定集

Robust Optimization and Adversary Resistant Learning

即稳健优化在机器学习中处理不确定性（随机的、对抗性的）

  • 稳健优化中在机器学习中应用

  • 稳健学习在很多学习任务中都有提出

    • 学习和规划
    • Fisher线性判别分析
    • PCA

这里考虑经典的二分类软阈值SVM

Corrupted Location

  • 椭圆不确定集：随机导致的

  • 正则化项使用

    • 传统的二范数，一范数同样使用的稀疏的解

  • 概率解释：风险控制

Missing Data

  • 多项式不确定：对抗删除数据（alpha go）

  • 使用无效特征消去偏置

  • 对max损失取对偶得到min带入得到SOCP

Robust Optimization and Regularization

  • 统一从稳健优化的角度解释学习算法中的优秀性质

    • 正则化
    • 稀疏
    • 一致性

  • 指导寻找新的算法

    • 大数定理、中心极限定理表明即使各个特征上随机不确定项 是独立的，其本身也会有强烈的耦合倾向，表现出相同特征 、像会相互影响一样

    • 这促使寻找新的稳健算法，其中随机不确定项是耦合的

SVM

Posted Updated Math Mixin16 minutes read (About 2380 words)

Kernel Function

Kernel Function

  • 对输入空间 $X$ （欧式空间 $R^n$ 的子集或离散集合）、特征空间 $H$ ，若存在从映射 $$
      \phi(x): X \rightarrow H

      K(x,z) = \phi(x) \phi(z)
    $$ 则称 $K(x,z)$ 为核函数、 $\phi(x)$ 为映射函数，其中 $\phi(x) \phi(z)$ 表示内积
  • 特征空间 $H$ 一般为无穷维
    • 特征空间必须为希尔伯特空间（内积完备空间）

映射函数 $\phi$

  • 映射函数 $\phi$：输入空间 $R^n$ 到特征空间的映射 $H$ 的映射

  • 对于给定的核 $K(x,z)$ ，映射函数取法不唯一，映射目标的特征空间可以不同，同一特征空间也可以取不同映射，如：

    • 对核函数 $K(x, y) = (x y)^2$ ，输入空间为 $R^2$ ，有

    • 若特征空间为$R^3$，取映射

      或取映射

    • 若特征空间为$R^4$，取映射

核函数 $K(x,z)$

  • Kernel Trick 核技巧：利用核函数简化映射函数 $\phi(x)$ 映射、内积的计算技巧

    • 避免实际计算映射函数
    • 避免高维向量空间向量的存储

  • 核函数即在核技巧中应用的函数

    • 实务中往往寻找到的合适的核函数即可，不关心对应的映射函数
    • 单个核函数可以对应多个映射、特征空间

  • 核技巧常被用于分类器中

    • 根据 Cover’s 定理，核技巧可用于非线性分类问题，如在 SVM 中常用
    • 核函数的作用范围：梯度变化较大的区域
      • 梯度变化小的区域，核函数值变化不大，所以没有区分能力
  • Cover’s 定理可以简单表述为：非线性分类问题映射到高维空间后更有可能线性可分

正定核函数

  • 设 $X \subset R^n$，$K(x,z)$ 是定义在 $X X$的对称函数，若 $\forall x_i \in \mathcal{X}, i=1,2,…,m$，$K(x,z)$ 对应的 Gram* 矩阵 $$
      G = [K(x_i, x_j)]_{m*m}
    $$ 是半正定矩阵，则称 $K(x,z)$ 为正定核
  • 可用于指导构造核函数
    • 检验具体函数是否为正定核函数不容易
    • 正定核具有优秀性质
      • SVM 中正定核能保证优化问题为凸二次规划，即二次规划中矩阵 $G$ 为正定矩阵

欧式空间核函数

Linear Kernel

线性核：最简单的核函数

  • 特点
    • 适用线性核的核算法通常同普通算法结果相同
      • KPCA 使用线性核等同于普通 PCA

Polynomial Kernel

多项式核：non-stational kernel

  • 特点

    • 适合正交归一化后的数据
    • 参数较多，稳定

      todo

  • 应用场合

    • SVM：p 次多项式分类器

Gaussian Kernel

高斯核：radial basis kernel，经典的稳健径向基核

  • $\sigma$：带通，取值关于核函数效果，影响高斯分布形状
    • 高估：分布过于集中，靠近边缘非常平缓，表现类似像线性一样，非线性能力失效
    • 低估：分布过于平缓，失去正则化能力，决策边界对噪声高度敏感

  • 特点

    • 对数据中噪声有较好的抗干扰能力

  • 对应映射：省略分母

    即高斯核能够把数据映射至无穷维

  • 应用场合

    • SVM：高斯radial basis function分类器

Exponential Kernel

指数核：高斯核变种，仅去掉范数的平方，也是径向基核

  • 降低了对参数的依赖性
  • 适用范围相对狭窄

Laplacian Kernel

拉普拉斯核：完全等同于的指数核，只是对参数$\sigma$改变敏感 性稍低，也是径向基核

ANOVA Kernel

方差核：径向基核

  • 在多维回归问题中效果很好

Hyperbolic Tangent/Sigmoid/Multilayer Perceptron Kernel

Sigmoid核：来自神经网络领域，被用作人工神经元的激活函数

  • 条件正定，但是实际应用中效果不错

  • 参数

    • $\alpha$：通常设置为$1/N$，N是数据维度
  • 使用Sigmoid核的SVM等同于两层感知机神经网络

Ration Quadratic Kernel

二次有理核：替代高斯核，计算耗时较小

Multiquadric Kernel

多元二次核：适用范围同二次有理核，是非正定核

Inverse Multiquadric Kernel

逆多元二次核：和高斯核一样，产生满秩核矩阵，产生无穷维的 特征空间

Circular Kernel

环形核：从统计角度考虑的核，各向同性稳定核，在$R^2$上正定

Spherical Kernel

类似环形核，在$R^3$上正定

Wave Kernel

波动核

  • 适用于语音处理场景

Triangular/Power Kernel

三角核/幂核：量纲不变核，条件正定

Log Kernel

对数核：在图像分隔上经常被使用，条件正定

Spline Kernel

样条核：以分段三次多项式形式给出

B-Spline Kernel

B-样条核：径向基核，通过递归形式给出

  • $x_{+}^d$：截断幂函数

Bessel Kernel

Bessel核：在theory of function spaces of fractional smoothness 中非常有名

  • $J$：第一类Bessel函数

Cauchy Kernel

柯西核：源自柯西分布，是长尾核，定义域广泛，可以用于原始维度 很高的数据

Chi-Square Kernel

卡方核：源自卡方分布

Histogram Intersection/Min Kernel

直方图交叉核：在图像分类中经常用到，适用于图像的直方图特征

Generalized Histogram Intersection

广义直方图交叉核：直方图交叉核的扩展，可以应用于更多领域

Bayesian Kernel

贝叶斯核：取决于建模的问题

Wavelet Kernel

波核：源自波理论

  • 参数

    • $c$：波的膨胀速率
    • $a$：波的转化速率
    • $h$：母波函数，可能的一个函数为

  • 转化不变版本如下

离散数据核函数

String Kernel

字符串核函数：定义在字符串集合（离散数据集合）上的核函数

  • $[\phin(s)]_n = \sum{i:s(i)=u} \lambda^{l(i)}$：长度 大于等于n的字符串集合$S$到特征空间 $\mathcal{H} = R^{\sum^n}$的映射，目标特征空间每维对应 一个字符串$u \in \sum^n$

  • $\sum$：有限字符表

  • $\sum^n$：$\sum$中元素构成，长度为n的字符串集合

  • $u = s(i) = s(i1)s(i_2)\cdots s(i{|u|})$：字符串s的 子串u（其自身也可以用此方式表示）

  • $i =(i1, i_2, \cdots, i{|u|}), 1 \leq i1 < i_2 < … < i{|u|} \leq |s|$：序列指标

  • $l(i) = i_{|u|} - i_1 + 1 \geq |u|$：字符串长度，仅在 序列指标$i$连续时取等号（$j$同）

  • $0 < \lambda \leq 1$：衰减参数

  • 两个字符串s、t上的字符串核函数，是基于映射$\phi_n$的 特征空间中的内积

    • 给出了字符串中长度为n的所有子串组成的特征向量的余弦 相似度
    • 直观上，两字符串相同子串越多，其越相似，核函数值越大
    • 核函数值可由动态规划快速计算（只需要计算两字符串公共 子序列即可）

  • 应用场合

    • 文本分类
    • 信息检索
    • 信物信息学
Posted Updated Probability2 minutes read (About 329 words)

概率不等式

Inequality

Azuma-Hoeffding Inequality

Azuma-Hoeffding 不等式：设 ${Xi:i=0,1,2,\cdots}$ 是鞅差序列，且 $|X_k - X{k-1}| < c_k$，则

Hoeffding Inequality

Hoeffding 不等式：考虑随机变量序列 $X_1, X_2, \cdots, X_N, X_i \in [a_i, b_i]$

  • 对随机变量 $\bar X = \frac 1 N \sum_{i=1}^N {X_i}$，对任意 $t>0$ 满足

  • 对随机变量 $SN = \sum{i=1}^N X_i$，对任意 $t>0$ 满足

  • 两不等式可用绝对值合并，但将不够精确

Bretagnolle-Huber-Carol Inequility

Bretagnolle-Huber-Carol 不等式：${X_i: i=1,2,\cdots,N} i.i.d. M(p1, p_2, \cdots, p_k)$ 服从类别为 $k$ 的多项分布

  • $N_i$：第 $i$ 类实际个数

Categories

Follow

Recents

Advertisement

follow.it

×