Loss Function

损失函数

• 损失函数可以视为模型与真实的距离的度量
  • 因此损失函数设计关键即，寻找可以代表模型与真实的距离的统计量
  • 同时为求解方便，应该损失函数最好应满足导数存在

Surrogate Loss

代理损失函数：用优化方便的损失函数代替难以优化的损失函数，间接达到优化原损失函数的目标

• 如 0-1 损失难以优化，考虑使用二次损失、交叉熵损失替代

损失函数设计

• 对有监督学习：真实 已知，可以直接设计损失函数

• 对无监督学习：真实 未知，需要给定 真实标准

  • NLP：需要给出语言模型
  • EM 算法：熵最大原理

常用损失函数

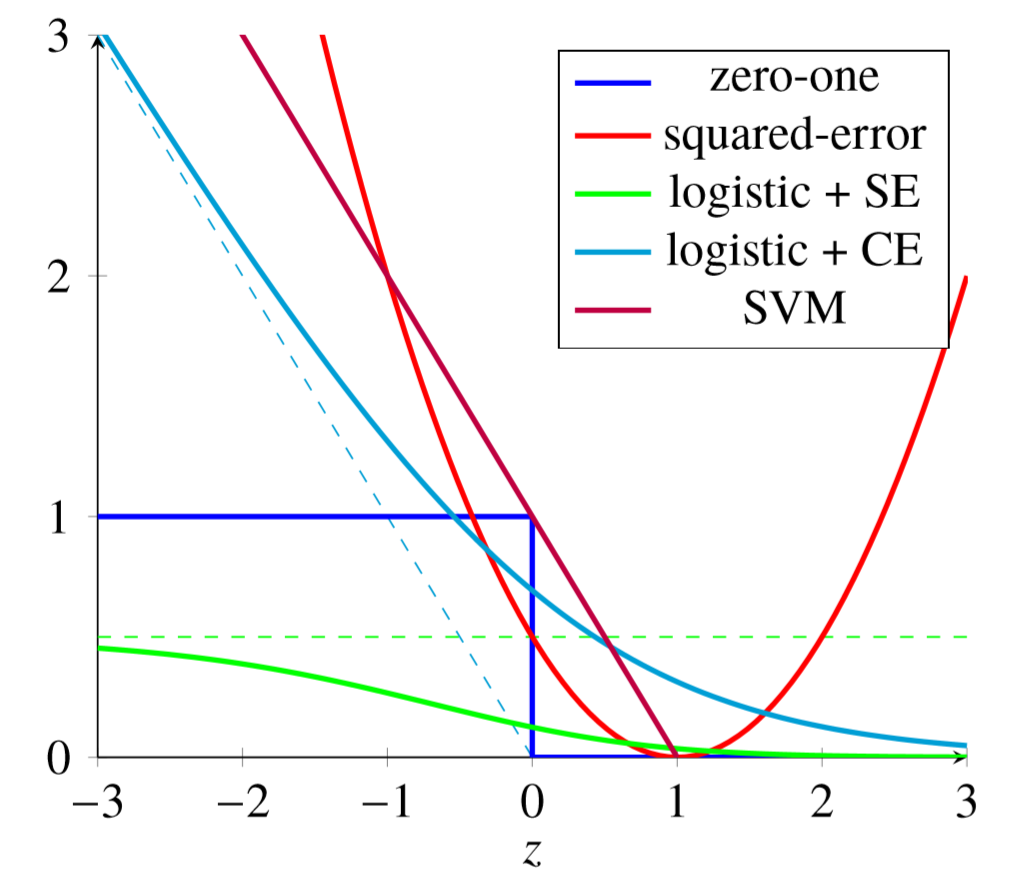
0-1 Loss

$$L(y, f(x)) = \left \{ \begin{array}{l} 1, & y \neq f(x) \\ 0, & y = f(x) \end{array} \right.$$

• 0-1 损失函数梯度要么为 0、要么不存在，无法通过梯度下降方法优化 0-1 损失

• 适用场合

  • 二分类：Adaboost
  • 多分类：Adaboost.M1

Quadratic / Squared Error Loss

$$L(y, f(x)) = \frac 1 2 (y - f(x))^2$$

• 平方错误损失函数可导，可以基于梯度下降算法优化损失函数

• 适用场合

  • 回归预测：线性回归
  • 分类预测：0-1 二分类（根据预测得分、阈值划分）

Logistic SE

• 平方损失用于二分类时存在如下问题（模型输出无限制）

  • 若模型对某样本非常确信为正例，给出大于1预测值
  • 此时模型会进行不必要、开销较大的优化

• 考虑对模型输出进行 sigmoid 变换后作为预测值，再应用平方错误损失函数

  $$L(y, f(x)) = \frac 1 2 (y - \sigma(f(x)))^2$$
  • Logistic SE 损失函数曲线对 0-1 损失拟合优于平方损失
  • 但负区间存在饱和问题，损失最大只有 0.5

Cross Entropy

交叉熵损失

$$\begin{align*} L(y, f(x)) & = -ylog(f(x)) \\ & = - \sum_{k=1}^K y_k log f(x)_k \end{align*}$$

• $y$：样本实际值
• $f(x)$：各类别预测概率
• $K$：分类数目

• 交叉熵损失综合二次损失、logistic SE 优势，以正样本为例

  • 预测值较大时：损失接近 0，避免无效优化
  • 预测值较小时：损失偏导趋近于 -1，不会出现饱和现象

• $y$ 为 one-hot 编码时实际值时

  • 分类问题仅某分量为 1：此时交叉熵损失同对数损失（负对数极大似然函数）
  • 标签问题则可有分量为 1

• 适合场合

  • 多分类问题
  • 标签问题

Hinge Loss

$$\begin{align*} L(y, f(x)) & = [1 - yf(x)]_{+} \\ [z]_{+} & = \left \{ \begin{array}{l} z, & z > 0 \\ 0, & z \leq 0 \end{array} \right. \end{align*}$$

• $y \in {-1, +1}$

• 合页损失函数：0-1 损失函数的上界，效果类似交叉熵损失函数

  • 要求分类不仅正确，还要求确信度足够高损失才为 0
  • 即对学习有更高的要求

• 适用场合

  • 二分类：线性支持向量机

收敛速度对比

• 指数激活函数时：相较于二次损失，收敛速度更快

• 二次损失对 $w$ 偏导

  $$\frac {\partial L} {\partial w} = (\sigma(z) - y) \sigma^{'}(z) x$$

  • $\sigma$：sigmoid、softmax 激活函数
  • $z = wx + b$

  • 考虑到 sigmoid 函数输入值绝对值较大时，其导数较小
  • 激活函数输入 $z=wx+b$ 较大时，$\sigma^{‘}(z)$ 较小，更新速率较慢

• Softmax 激活函数时，交叉熵对 $w$ 偏导

  $$\begin{align*} \frac {\partial L} {\partial w} & = -y\frac 1 {\sigma(z)} \sigma^{'}(z) x \\ & = y(\sigma(z) - 1)x \end{align*}$$

• 特别的，对 sigmoid 二分类

  $$\begin{align*} \frac {\partial L} {\partial w_j} & = -(\frac y {\sigma(z)} - \frac {(1-y)} {1-\sigma(z)}) \sigma^{'}(z) x \\ & = -\frac {\sigma^{'}(z) x} {\sigma(z)(1-\sigma(z))} (\sigma(z) - y) \\ & = x(\sigma(z) - y) \end{align*}$$
  • 考虑 $y \in {(0,1), (1,0)}$、$w$ 有两组
  • 带入一般形式多分类也可以得到二分类结果

不常用损失函数

Absolute Loss

绝对损失函数

$$L(y, f(x)) = |y-f(x)|$$

• 适用场合
  • 回归预测

Logarithmic Loss

对数损失函数（负对数极大似然损失函数）

$$L(y, P(y|x)) = -logP(y|x)$$

• 适用场合
  • 多分类：贝叶斯生成模型、逻辑回归

Exponential Loss

指数函数函数

$$L(y, f(x)) = exp\{-yf(x)\}$$

• 适用场合
  • 二分类：前向分步算法

Pseudo Loss

伪损失：考虑个体损失 $(x_i, y_i)$ 如下，据此构造伪损失

• $h(x_i, y_i)=1, \sum h(x_i, y)=0$：完全正确预测
• $h(x_i, y_i)=0, \sum h(x_i, y)=1$：完全错误预测
• $h(x_i, y_i)=1/M$：随机预测（M为分类数目）

$$L(y, f(x)) = \frac 1 2 \sum_{y^{(j)} \neq f(x)} w_j (1 - f(x, y) + f(x, y^{(j)}))$$

• $w_j$：样本个体错误标签权重，对不同个体分布可不同
• $f(x, y^{(j)})$：分类器将输入 $x$ 预测为第 $j$ 类 $y^{(j)}$ 的置信度

• 伪损失函数考虑了预测 标签 的权重分布

  • 通过改变此分布，能够更明确的关注难以预测的个体标签，而不仅仅个体

• 伪损失随着分类器预测准确率增加而减小

  • 分类器 $f$ 对所有可能类别输出置信度相同时，伪损失最大达到 0.5，此时就是随机预测
  • 伪损失大于 0.5 时，应该将使用 $1-f$

• 适用场景

  • 多分类：Adaboost.M2