Stacked Generalization

Stacked Generalization

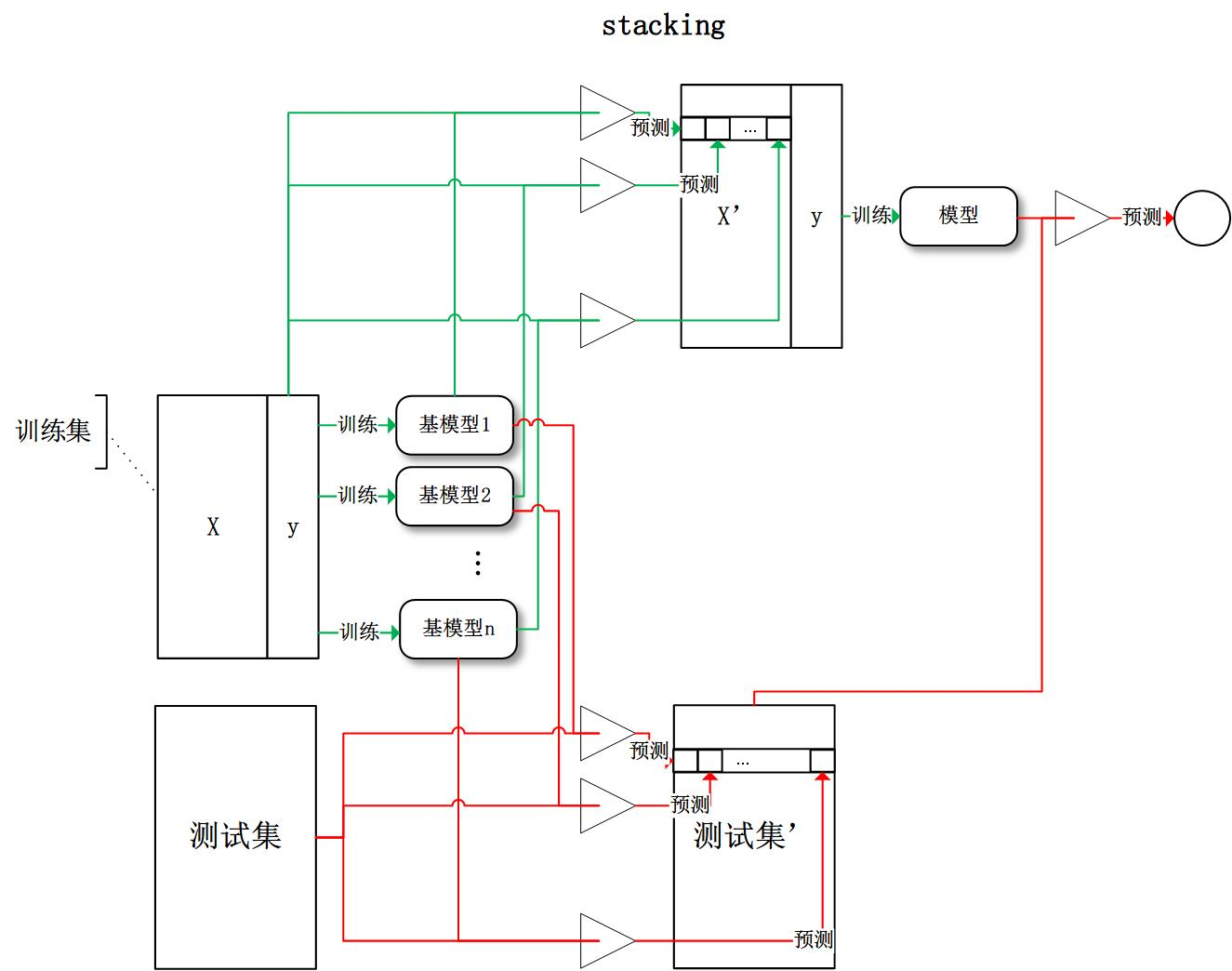
堆栈泛化：使用多种模型分别训练训练，将其结果叠加作为下层 模型的输入，最终得到预测输出

• 属于异源集成模型，可以视为

  • 复合函数

    

  • 短路网络

    

• 从某种意义上，复杂模型都是stacking

思想

• 不同模型侧重于获取数据不同方面的特征

  • 使用基学习器抽取数据特征进行表示学习，提取不同角度的 数据高维特征
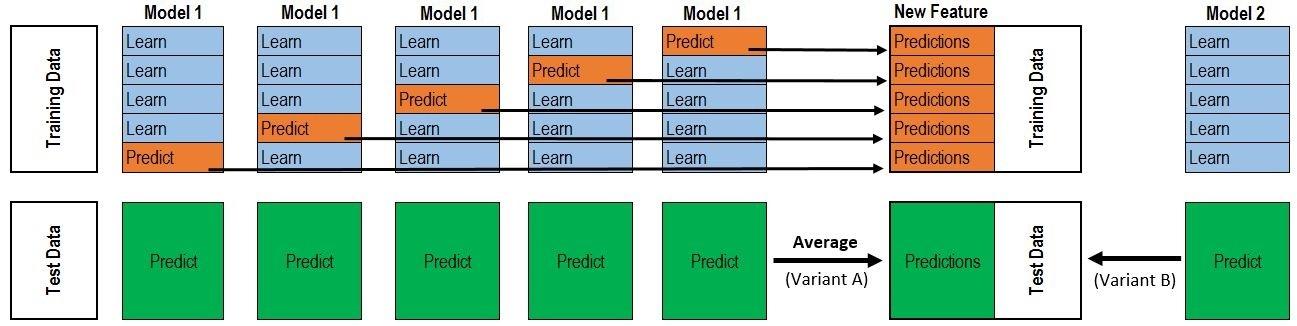
  • 考虑到使用全量训练数据训练、预测作为下层模型输入会 导致过拟合，可使用K折交叉验证避免过拟合
  • 有些基学习器只使用适合其部分特征训练
    • GBDT、DNN适合低维稠密特征

• 元学习器组合多个基学习器的输出

  • 从数据高维特征学习数据模式，具有更好的泛化能力，避免 过拟合

算法

• 输入：模型$M1, M_2, \cdots, M_d$、训练特征：$X{n*m}$、 训练标签$Y_{n}$、测试特征$X^{‘}$
• 输出：stacking模型、预测标签

• 将训练数据K折划分，对第$i$轮划分

  • 使用模型$M1, M_2, \cdots, M_d$分别在相应训练集 $[X[:n_i,:], X[n{i+1}:,:]]$、 $[Y[:ni], Y[n{i+1}:]]$上训练
  • 在相应验证集$X[ni:n{i+1}, :]$上验证、并记录验证 结果
  • 将验证集验证结果叠加得到部分样本新特征 $N[ni: n{i+1}, d]$

• 将K轮划分得到的部分新特征拼接得到训练集的完整新特征 $N_{n * d}$，将新特征作为输入，训练下层模型，得到最终 stacking模型

• 将测试特征如上作为输入经过两层模型预测，得到最终预测结果

• 以上以2层stacking为例，有深层stacking

常用模型

基学习器

• 交叉项、原始特征本身也可以视为线性基学习器学习到的特征

• 具体模型参见 ml_specification/rec_system/ctr_stacking_models

GBDT

• 各树中各节点对应元学习器一维输入特征

• 适合低维稠密通用特征，对输入特征分布没有要求

• GBDT树根据熵增益（Gini系数增益）划分节点，每条路径 都代表一定区分能力

  • 以叶子节点（路径）作为特征，相当于自动进行特征 转换、组合、选择、离散化，得到高维组合特征

• GDBT相较于单棵树、或RF更适合stacking

  • 单棵树表达能力弱，无法表达多个有区分性特征组合， 集成模型可将样本映射为多个特征
  • GBDT拟合残差意味着各树对样本区分度不同，对各特征 区别对待更合理

DNN

• 适合普通稠密特征、embedding特征
• 模型表达能力强，能抽取有良好分布数据的深层次特征，提高 模型准确性、泛化能力
• 容易扩充其他类别特征，如：图片、文字

元学习器

• LR

  • 适合低维稀疏特征，可对所有特征离散化以引入非线性

• FM

  • 适合低维稀疏特征
  • LR基础上自动组合二阶交叉项

• Linear：训练模型、对训练结果线性加权

?