Proximal Gredient Method
Proximal Operator
- $f(x)$:凸函数
- 由于$L_2$范数的强凸性,近端算子也强凸,解总是唯一存在
- 直观理解:寻找距离点$x$不太远、$f(u)$尽可能小的$u$
- 以下算法都是近端算法的特例
- shrinkage thresholding algorithm
- projected Landweber
- projected gradient
- alternating projections
- alternating-directions method of multipliers
- alternating split Bregman
- 近端算子连续可微
Moreau Envolop
- $\gamma > 0$:平衡参数,$\gamma = 1$即为普通近端算子
近端算子求解
对一般凸$f(x)$,通常使用次梯度进行优化,其近端算子解为 (即解变动方向$p-x$为负次梯度方向)
对光滑凸函数$f$,上述等式对其近端算子约简为 (即解变动方向$p-x$为负梯度方向)
性质
分离函数
取$f(x) = |x|_1$,即可得即软阈值算子
- 参考坐标下降:近端算子中二次项中各分量无关,所以一轮 迭代即为最优解
仿射函数分解
- $A^T A = \alpha I, \alpha > 0$:线性变换
- $g$:良好闭凸函数
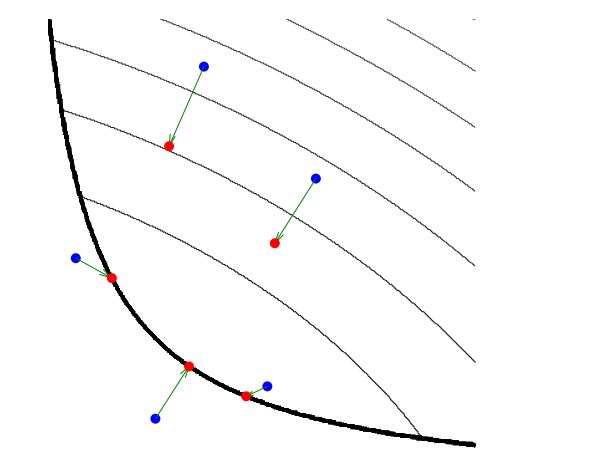
第一投影定理
- 取$f(x)$为示性函数、约束条件,即得到投影算子
第二临近定理
- $f$为良好闭凸函数,则以下三条等价
- $y = prox_f(x)$
- $x - y \in \partial f(y)$:由近端算子定义即得
- $\forall z,
\leq f(z) - f(y)$
Moreau Decomposition
最小值
证明
- $x_f = \arg\min_x f(x)$
- $x_p = \arg\min_x prox_f(x)$
例
- $f(x)=c$:
Projection Operator
投影算子
- 点$x$在凸集$C$上的投影:$X$上距离$x$的欧式距离最近的点
Alternating Projection Method
POCS/project onto convex sets method:用于解同时满足多个 凸约束的算法
$f_i$作为非空闭凸集$C_i$示性函数,表示一个约束,则整个 问题约简为convex feasibility problem
只需要找到位于所有$C_i$交集的解即可
每次迭代
- 在其他问题中投影算子不再适合,需要更一般的算子,在其他 各种同样的凸投影算子中,近端算子最合适
Proximal Gradient Method
近端算法:分两步分别优化可微凸$F(x)$、凸$R(x)$,近似优化目标 函数整体,不断迭代直至收敛
- $F(x)$:可微、凸函数
- $\nabla F(x)$:Lipschitz continous、利普希茨常数为$L$
- $R(x)$:下半连续凸函函数,可能不光滑
- $\mathcal{H}$:目标函数定义域集合,如:希尔伯特空间
gredient step:从$x^{(k)}$处沿$F(x)$负梯度方向微小移动 达到$x^{(k.5)}$
proximal operator step:在$x^{(k.5)}$处应用$R(x)$近端 算子,即寻找$x^{(k.5)}$附近且使得$R(x)$较小点
目标函数推导
- $\frac {\gamma} 2 |\nabla F(x)|_2^2, F(x)$:与$u$无关 ,相互替换不影响极值
- $0 < \gamma \leq \frac 1 L$:保证最后反向泰勒展开成立
则$prox_{\gamma R}(x-\gamma \nabla F(x))$解即为 “原问题最优解”(若泰勒展开完全拟合$F(x)$)
- 近端算法中距离微调项部分可加法分离
- 若$R(x)$部分也可分离,则整个目标函数可以分离,可以 拆分为多个一元函数分别求极值
考虑泰勒展开是局部性质,$u$作为极小值点只能保证在$x$附近 领域成立,可将近端算子解作为下个迭代点
迭代终止条件即
二阶近似证明
- $\nabla^2 F(\zeta)$:凸函数二阶导正定
- $|\nabla F(u) - \nabla F(x)|_2 \leq L |u-x|_2$: $\nabla F(x)$利普希茨连续性质
参数确定
$L$已知时,可直接确定$\gamma \in (0, \frac 1 L]$,
否则可线性迭代搜索$\gamma := \beta \gamma,\beta < 1$, 直至
- $PG{\gamma R}(x)=x-prox{\gamma R}(x-\gamma \nabla F(x))$
- 直接根据下述利普希茨条件须求Hasse矩阵,计算量较大
反向推导
对$F(x)+R(x)$在$x_0$附近作泰勒展开
- $\lambda \in (0, \frac 1 L]$
- $L$:$F(x)$利普希茨常数
- $\leq$:由Lipschitz连续可取
- 则不等式右边就是$F(x)+R(x)$的一个上界,可以对将对其 求极小化转化对此上界求极小
考虑对极小化目标添加常数项不影响极值,对不等式右侧添加 与$u$无关项$\frac \gamma 2 |\nabla F(x)|_2^2$、剔除 剔除$F(x)$凑出近端算子
近端算法推广
问题推广
- 求解non-differentiable凸优化问题的通用投影形式
- $f_i(x)$:凸函数,不一定处处可微
目标函数中包含不处处连续可微函数,整个目标函数不光滑
- 无法使用传统的光滑优化手段,如:最速下降、共轭梯度
- 极小化条件为$0 \in \partial(F+R)(x)$
分开考虑各个函数,对非光滑函数使用近端算子处理
算子推广
- 考虑使用Bregman Divergence替代近端算子中欧式距离
- 取$\mu(x) = \frac 1 2 |x|_2^2$时,即为普通近端算子