Line Search
综述
一维搜索/线搜索:单变量函数最优化,即求一维问题
最优解的$\alpha_k$的数值方法
exact line search:精确一维搜索,求得最优步长 $\alpha_k$使得目标函数沿着$d^{(k)}$方向达到极小,即
inexact line search:非精确一维搜索,求得$\alpha_k$ 使得
一维搜索基本结构
- 确定搜索区间
- 用某种方法缩小搜索区间
- 得到所需解
搜索区间
- 搜索区间:设$\alpha^{ }$是$\phi(\alpha)$极小点,若存在 闭区间$[a, b]$使得$\alpha^{ } \in [a, b]$,则称 $[a, b]$是$phi(\alpha)$的搜索区间
确定搜索区间的进退法
取初始步长$\alpha$,置初始值
置
若$\phi < \phi_3$,置
若k =1,置
转2,否则置
并令$a=min{\mu_1,\mu_3}, b=max{\mu_1,\mu_3}$,停止搜索
- 通常认为目标函数此算法得到搜索区间就是单峰函数
试探法
- 在搜索区间内选择两个点,计算目标函数值
- 需要获得两个点取值才能判断极值点的所属区间
- 去掉函数值较大者至离其较近端点段
0.618法
置初始搜索区间$[a, b]$,置精度要求$\epsilon$,计算左右 试探点
其中$\tau = \frac {\sqrt 5 - 1} 2$,及相应函数值
若$\phi_l<\phi_r$,置
并计算
否则置
并计算
若$|b - a| \geq \epsilon$
- 若$\phi_l < \phi_r$,置$\mu = a_l$
- 否则置$\mu = \alpha_r$ 得到问题解$\mu$,否则转2
- 0.618法除第一次外,每次只需要计算一个新试探点、一个新 函数值,大大提高了算法效率
- 收敛速率线性,收敛比为$\tau = \frac {\sqrt 5 - 1} 2$常数
Fibonacci方法
置初始搜索区间$[a, b]$,置精度要求$\epsilon$,选取分离 间隔$\sigma < \epsilon$,求最小正整数n,使得 $F_n > \frac {b - a} \epsilon$,计算左右试探点
$\begin{align} al & = a + \frac {F{n-2}} {Fn} (b - a)\ a_r & = a + \frac {F{n-1}} {F_n} (b - a) \end{align}
置n=n-1
若$\phi_l < \phi_r$,置
若n>2,计算
否则计算
若$\phi_l \geq \phi_r$,置
若n>2,计算
否则计算
若n=1
- 若$\phi_l < \phi_r$,置$\mu = a_r$
- 否则置$\mu = a_r$
得到极小点$\mu$,停止计算,否则转2
- Finonacci方法是选取实验点的最佳策略,即在实验点个数相同 情况下,最终的极小区间最小的策略
- Finonacci法最优性质可通过设最终区间长度为1,递推使得原始 估计区间最大的取实验点方式,得出
插值法
- 利用搜索区间上某点的信息构造插值多项式(通常不超过3次) $\hat \phi(\alpha)$
- 逐步用$\hat \phi(\alpha)$的极小点逼近$\phi(\alpha)$ 极小点$\alpha^{*}$
- $\phi^{ * }$解析性质比较好时,插值法较试探法效果好
三点二次插值法
思想
以过三个点$(\mu_1,\phi_1), (\mu_2,\phi_2), (\mu_3,\phi_3)$ 的二次插值函数逼近目标函数
求导,得到$\hat \phi(\alpha)$的极小点
若插值结果不理想,继续构造插值函数求极小点近似值
算法
取初始点$\mu_1<\mu_2<\mu_3$,计算$\phi_i=\phi(\mu_i)$, 且满足$\phi_1 > \phi_2, \phi_3 > \phi_2$,置精度要求 $\epsilon$
计算
- 若A=0,置$\mu = \mu_2, \phi = \phi_2$,停止计算, 输出$\mu, \phi$
计算
- 若$\mu<\mu_1 或 \mu>\mu_3,\mu \notin (\mu_1,\mu_3)$ ,停止计算,输出$\mu, \phi$
计算$\phi = \phi(\mu)$,若$|\mu - \mu_2| < \epsilon$, 停止计算,得到极小点$\mu$
若$\mu \in (\mu_2, \mu_3)$
- 若$\phi < \phi_2$,置
- 否则置
否则
若$\phi < \phi_2$,置
否则置
转2
两点二次插值法
思想
以$\phi(\alpha)$在两点处$\mu_1, \mu_2$函数值 $\phi_1=\phi(\mu_1)$、一点处导数值 $\phi_1^{‘}=\phi^{‘}(\mu_1) < 0$构造二次函数逼近原函数
为保证$[\mu_1, \mu_2]$中极小点,须有 $\phi_2 > \phi_1 + \phi_1^{‘}(\mu_2 - \mu_1)$
求解,得到$\hat \phi (\mu)$极小值为
若插值不理想,继续构造插值函数求极小点的近似值
算法
初始点$\mu_1$、初始步长$d$、步长缩减因子$\rho$、精度要求 $\epsilon$,计算
若$\phi_1^{‘} < 0$,置$d = |d|$,否则置$d = -|d|$
计算
若$\phi_2 \leq \phi_1 + \phi_1^{‘}(\mu_2 - \mu_1)$,置 $d = 2d$,转3
计算
若$|phi^{‘}| \leq \epsilon$,停止计算,得到极小点$\mu$, 否则置
- 其中通常取$d = 1, \rho = 0.1$
两点三次插值法
原理
以两点$\mu_1, \mu_2$处函数值$\phi_i = \phi(\mu_i)$和其导数值 $\phi_i^{‘} = \phi^{‘}(\mu_i)$,由Himiter插值公式可以构造 三次插值多项式$\hat \phi(\alpha)$
求导置0,得到$\hat \phi(\alpha)$极小点
算法
初始值$\mu_1$、初始步长$d$、步长缩减因子$\rho$、精度要求 $\epsilon$,计算
若$\phi_1^{‘} > 0$,置$d = -|d|$,否则置$d = |d|$
置$\mu_2 = \mu_1 + \alpha$,计算
若$\phi_1^{‘} \phi_2{‘} > 0$,置
转3
计算
若$|\phi^{‘}| < \epsilon$,停止计算,得到极小点$\mu$, 否则置
转2
- 通常取$d = 1, \rho = 0.1$
非精确一维搜索
对无约束问题整体而言,又是不要求得到极小点,只需要一定 下降量,缩短一维搜索时间,使整体效果最好
求满足$\phi(\mu) < \phi(0)$、大小合适的$\mu$
- $\mu$过大容易不稳定
- $\mu$过小速度慢
GoldStein方法
原理
预先指定精度要求$0< \beta_1 < \beta_2 < 1$
以以下不等式限定步长
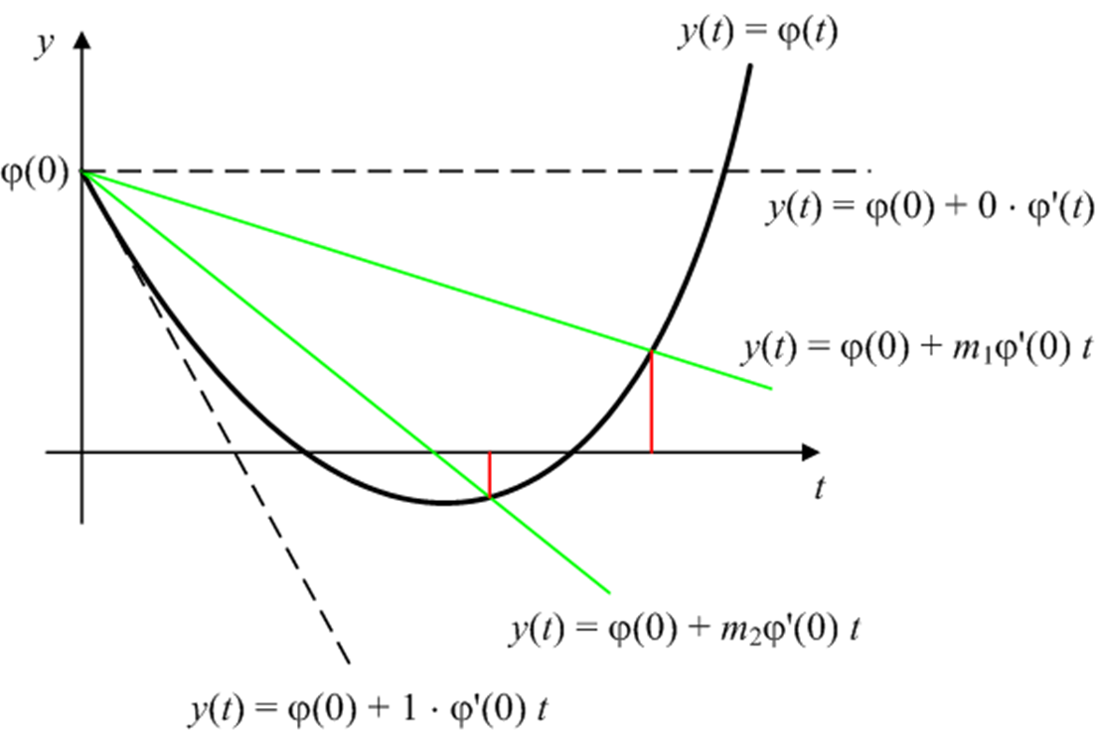
算法
初始试探点$\mu$,置$\mu{min} = 0, \mu{max} = \infty$, 置精度要求$0 < \beta_1 < \beta_2 < 1$
对$\phi(mu)$
若$\phi(\mu) > \phi(0) + \beta1 \phi^{‘}(0) \mu$, 置$\mu{max} = \mu$
否则若$\phi(\mu) > \phi(0) + \beta_2 \phi^{‘}(0)\mu$ ,则停止计算,得到非精确最优解$\mu$
否则置$\mu_{min} = \mu$
若$\mu{max} < \infty$,置 $\mu = \frac 1 2 (\mu{min} + \mu{max})$,否则置 $\mu = 2 \mu{min}$
转2
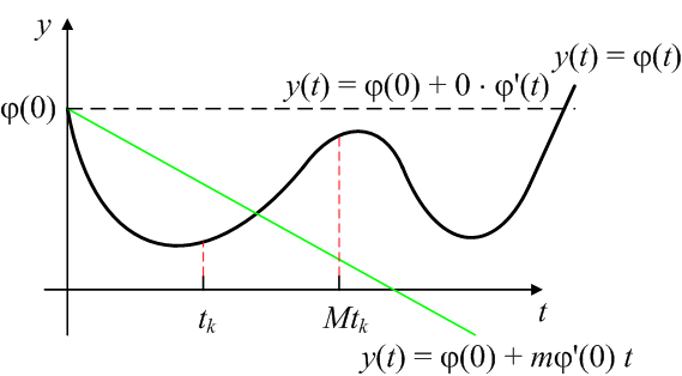
Armijo方法
Armijo方法是Goldstein方法的变形
预先取$M > 1, 0 < \beta_1 < 1$
选取$\mu$使得其满足以下,而$M\mu$不满足
- M通常取2至10
Wolfe-Powell方法
预先指定参数$0 < \beta_1 < \beta_2 <1$
选取$\mu$满足
- 能保证可接受解中包含最优解,而Goldstein方法不能保证