Word2Vec
Word2Vec
Word2Vec:word embeding的一种,使用层次化softmax、负采样 训练词向量
Hierarchical Softmax
层次Softmax
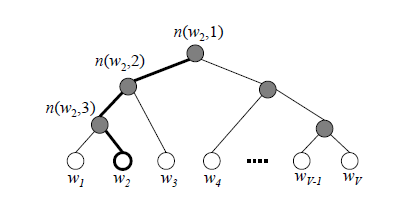
对所有词向量求和取平均作为输入层到隐层的映射 (特指CBOW模型)
使用霍夫曼树代替从隐藏层到输出softmax层的映射
思想
softmax需要对$m$个类别求出softmax概率,参数多、计算复杂
考虑将$m$个类别划分为多个二分类sigmoid,即
- 将总类别划分为两组
- 依次判断数据点属于哪组
- 直至数据点所属组仅包含一个类别
则多个sigmoid划分构成一棵二叉树,树叶子节点即为$m$ 类别
- 二叉树结构可以由多种,最优二叉树应该使得对整个 数据集而言,sigmoid判断次数最少
- 即应该使用按照数据点频数构建的霍夫曼树
- 霍夫曼树
模型
输入$x^T$所属类别霍夫曼编码为$d={d_1,\cdots,d_M}$, 则应最大化如下似然函数
- $w_j, b_j$:节点$j$对应sigmoid参数
- $P(d_i)$:以sigmoid激活值作为正例概率 (也可以其作为负例概率,但似然函数需更改)
则对数似然函数为
梯度计算
则参数$w_{j_M}$梯度如下
词向量$x$梯度如下
CBOW流程
- 特征词周围上下文词均使用梯度更新,更新输入
- 基于预料训练样本建立霍夫曼树
- 随机初始化模型参数$w$、词向量$w$
对训练集中每个样本 $(context(x), x)$($2C$个上下文)如下 计算,直至收敛
置:$e=0, xw=\frac 1 {2C} \sum{c=1}^{2C} x_c$
对$x$的霍夫曼编码 $d={d_1, \cdots, d_M}$ 中 $d_i$ 计算
更新 $2C$ 上下文词对应词向量
Skip-Gram流程
- 考虑上下文是相互的,则 $P(x{context}|x)$ 最大化时,$P(x|x{context})$ 也最大
- 为在迭代窗口(样本)内更新仅可能多词向量,应该最大化 $P(x|x_{context})$,使用梯度更新上下文 $2C$ 个词向量,更新输出(条件概率中更新条件)
- 基于预料训练样本建立霍夫曼树
- 随机初始化模型参数 $w$、词向量 $w$
对训练集中每个样本 $(x, context(x))$、每个样本中上下文词向量 $x_c$($2C$ 个上下文),训练直至收敛
置:$e=0$
对 $x$ 的霍夫曼编码 $d={d_1, \cdots, d_M}$ 中 $d_i$ 计算
更新 $2C$ 上下文词对应词向量
Negtive Sampling
负采样
思想
- 通过负采样得到$neg$个负例
- 对正例、负采样负例建立二元逻辑回归
模型、梯度
对类别为$j$正例、负采样负例应有如下似然函数、对数似然 函数
- $y_i$:样本点标签,$y_0$为正例、其余负例
同普通LR二分类,得到参数、词向量梯度
负采样方法
每个词对应采样概率为词频取$3/4$次幂后加权
CBOW流程
- 随机初始化所有模型参数、词向量
- 对每个训练样本$(context(x_0), x_0)$负采样$neg$个中心词 $x_i$,考虑$x_0$为类别$j$
在以上训练集$context(x0), x_0, x_1, \cdots, x{neg}$中 训练直至收敛
置:$e=0, xw=\frac 1 {2C} \sum{c=1}^{2C} x_c$
对样本$x0, x_1, \cdots, x{neg}$,计算
更新$2C$上下文词对应词向量
Skip-gram中心词
- 类似Hierarchical Softmax思想,更新输出$2C$个词向量
- 随机初始化所有模型参数、词向量
- 对每个训练样本$(context(x_0), x_0)$负采样$neg$个中心词 $x_i$,考虑$x_0$为类别$j$
以上训练集$context(x0), x_0, x_1, \cdots, x{neg}$中, 对每个上下文词向量$x_c$如下训练直至收敛
置:$e=0$
更新$2C$上下文词对应词向量