LightGBM

Truncated Gradient

L1正则化法

L1正则化

• $\lambda$：正则化项参数
• $sgn$：符号函数
• $g^{(t)}=\nabla_w L(w^{(t)}, Z^{(t)})$：损失函数对参数梯度

• L1正则化项在0处不可导，每次迭代使用次梯度计算正则项梯度
• OGD中每次根据观测到的一个样本进行权重更新 （所以后面正则项次梯度只考虑非0处？？？）

简单截断法

简单截断法：以$k$为窗口，当$t/k$非整数时，使用标准SGD迭代， 否则如下更新权重

• $w^{(t)}$：模型参数
• $g^{(t)}$：损失函数对模型参数梯度
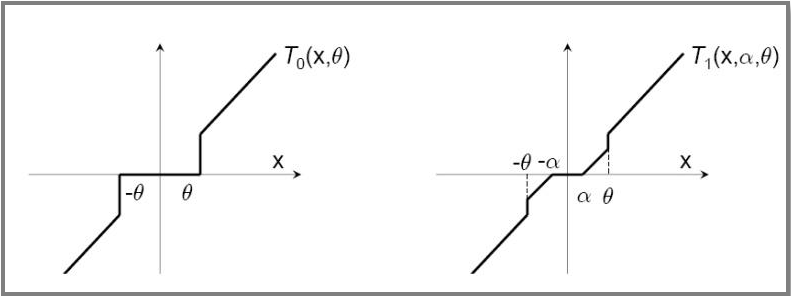
• $T_0$：截断函数
• $\theta$：控制参数稀疏性

截断梯度法

截断梯度法：以$k$为窗口，当$t/k$非整数时，使用标准SGD迭代， 否则如下更新权重

• $\lambda, \theta$：控制参数$w$稀疏性

• 对简单截断的改进，避免在实际（OgD）中参数因训练不足过小 而被错误截断，造成特征丢失

  

Forward-Backward Spliting

FOBOS：前向后向切分，权重更新方式为proximal method如下

L1-FOBOS

L1-FOBOS：即令$Phi(w)=\lambda |w|_1$，则根据可加性如下

• $V=[v_1, v_2, \cdots, v_N]:=w^{(t.5)}$：为方便
• $\tilde \lambda := \eta^{t.5} \lambda$：为方便
• $\eta^{t.5}$：学习率，常取 $\eta^{(t)} \in \theta(\frac 1 {\sqrt t})$

• 则对$w_i$求次梯度、分类讨论，解得

  $$w_i^{(t+1)} = \left \{ \begin{array}{l} v_i - \tilde \lambda, & v_i > \tilde \lambda \\ 0, & |v_i| < \tilde \lambda \\ v_i + \tilde \lambda, & v_i < -\tilde \lambda \end{array} \right.$$

  • 可以理解为：到当前样本为止，维度权重小于阈值 $\eta^{(t.5)} \lambda$）时，认为该维度不够重要， 权重置为0

  • 可视为$k=1, \theta=\infty$的Tg算法

• 另外，显然有$w_i^{(t+1)} v_i \geq 0$

  $$\begin{align*} \frac 1 2 (w_i^{(t+1)} - v_i)^2 + \tilde \lambda |w_i^{(t+1)}| & = \frac 1 2((w_i^{(t+1)})^2 - 2 w_i^{(t+1)} v_i + v_i^2) + \tilde \lambda |w_i^{(t+1)}| \\ & \leq \frac 1 2 v_i^2 \end{align*}$$

  • 考虑$w_i^{(t+1)}$使得目标函数最小，带入$w=0$则得

Regularized Dual Averaging

RDA算法：正则对偶平均算法，权重更新方式为 包含[增广]正则项的最速下降

• 目标函数包括三个部分

  • $\frac 1 t \sum_{r=1}^t g^{(r)} w$：包含之前所有梯度 均值
  • $\Phi(w)$：正则项
  • $\frac {\beta^{(t)}} t h(w)$：额外正则项，严格凸，且 不影响稀疏性

• 相较于TG、FOBOS是从另一方面求解在线最优化，更有效地提升 特征权重稀疏性

L1 RDA

L1 RDA：令$\Phi(w) := \lambda |w|_1$， 再设$h(w) := |w|_2^2$，根据可加性则有

• $\lambda > 0, \gamma > 0$
• $\bar gi^{(t)} = \frac 1 t \sum{r=1}^t g_i^{(r)}$

• 对$w_i$求次梯度、置零、求解得

  $$w_i^{(t+1)} = \left \{ \begin{array}{l} -\frac {\sqrt t} {\gamma} (\bar g^{(t)} - \lambda), & \bar g_i^{(t)} > \lambda \\ 0, & |\bar g_i^{(t)}| \leq \lambda \\ -\frac {\sqrt t} {\gamma} (\bar g^{(t)} + \lambda), & \bar g_i^{(t)} < -\lambda \\ \end{array} \right.$$
  • 可以理解为：某维度梯度累计均值绝对值$|bar g_i^{(t)}$ 小于阈值$\lambda$时，对应权重被置零、产生稀疏性

• 相较于L1-FOBOS的截断

  • 截断阈值为常数，更加激进、容易产生稀疏性
  • 截断判断对象为梯度累加均值，避免由于训练不足而产生 截断
  • 只需条件$\lambda$参数，容易权衡精度、稀疏性

Follow the Regularized Leader

FTRL：综合考虑L1-RDA、L1-FOBOS

L1-FOBOS、L1-RDA变换

• 将L1-FOBOS类似近端算法收敛证明中展开、去除无关项、放缩， 得到类似L1-RDA目标函数

  $$\begin{align*} w^{(t+1)} & = \arg\min_w \{ \frac 1 2 \|w - w^{(t)} + \eta^{(t)} g^{(t)}\| + \eta^{(t)} \lambda \|w\|_1 \} \\ & = \arg\min_w \{ g^{(t)} w + \lambda \|w\|_1 + \frac 1 {2 \eta^{(t)}} \|w - w^{(t)}\|_2^2 \} \end{align*}$$

• 将L1-RDA目标函数整体整体放缩，得到

  $$w^{(t+1)} = \arg\min_w \{ g^{(1:t)} w + t \lambda \|w\|_1 + \frac 1 {2\eta^{(t)}} \|w - 0\|_2^2 \}$$

  • $g^{(1:t)} := \sum_{r=1}^t g^{(r)}$

• FTRL综合考虑L1-FOBOS、L1-RDA，得到目标函数

  $$w^{(t+1)} = \arg\min_w \{ g^{(1:t)} W + \lambda_1 \|w\|_1 + \frac {\lambda_2} 2 \|w\|_2^2 + \frac 1 2 \sum_{r=1}^t \sigma^{(r)} \|w - w^{(r)}\|_2^2 \}$$
  • 使用累加梯度更新，避免因训练不充分错误截断
  • 包含L1-FOBOS、L1-RDA全部正则化项

求解

• 将FTRL中最后一项拆分、去除无关项

  $$\begin{align*} w^{(t+1)} & = \arg\min_w \{(g^{(1:t)} - \sum_{r=1}^t \sigma^{(r)} w^{(r)})w + \lambda_1 \|w\|_1 + \frac 1 2 (\lambda_2 + \sum_{r=1}^t \sigma^{(r)}) \|w\|_2^2 + \frac 1 2 \sum_{r=1}^t \sigma^{(r)} \|w^{(r)}\|_2^2 \} \\ & = \arg\min_w \{ z^{(t)} w + \lambda_1 \|w\|_1 + \frac 1 2 (\lambda_2 + \sum_{r=1}^t \sigma^{(r)}) \|w\|_2^2 \} \\ z^{(t)} &= g^{(1:t)} - \sum_{r=1}^t \sigma^{(r)} w^{(r)} \end{align*}$$

• 则同样根据可加性，对各分量求次梯度、置零、求解得

  $$w_i^{(t+1)} = \left \{ \begin{array}{l} \frac 1 {\lambda_1 + \sum_{r=1}^t \sigma^{(r)}} (z_i^{(t)} - \lambda_1 z_i), & z_i > \lambda_1 \\ 0, & |z_i^{(t)}| \leq \lambda_1 \\ \frac 1 {\lambda_1 + \sum_{r=1}^t \sigma^{(r)}} (z_i^{(t)} + \lambda_1 z_i), & z_i < -\lambda_1 \\ \end{array} \right.$$

• 其中学习率$\eta$为类似Adagrad优化器的学习率，但包括可学习 参数$\alpha, \beta$

  $$\eta_i^{(t)} = \frac {\alpha} {\beta + \sqrt{\sum_{r=1}^t (g_i^{(r)})^2}}$$

参数估计

• 矩估计：建立参数和总体矩的关系，求解参数

  • 除非参数本身即为样本矩，否则基本无应用价值
  • 应用场合
    • 均值：对应二次损失 $\arg\min{\mu} \sum{i=1}^N (x_i - \mu)^2$
    • 方差：对应二次损失?

• 极大似然估计：极大化似然函数，求解概率上最合理参数

  • 需知道（假设）总体 概率分布形式
  • 似然函数形式复杂，求解困难
    • 往往无法直接给出参数的解析解，只能求数值解
  • 应用场合
    • 估计回归参数：对数损失 $\mathop{\arg\min}{\beta} \sum{i=1}^N lnP(y_i|x_i, \beta)$

• 损失函数估计：极小化损失函数，求解损失最小的参数

  • 最泛用的参数求解方法
    • 适合求解有大量参数的待求解的问题
    • 往往通过迭代方式逐步求解
  • 特别的
    • 线性回归使用 MSE 作为损失函数时，也被称为最小二乘估计
    • 极大似然估计同对数损失函数

• 参数估计都可以找到合适损失函数，通过迭代求解损失最小化

随机模拟估计参数

• 需要设计随机模拟实验估计参数
• 应用场合
  • 蒙特卡洛类似算法：随机化损失

迭代求解参数

• 损失函数定义不同

  • 包含样本量数量不同
  • 惩罚项设置不同

• 异步更新参数

  • 同时求解参数数量：全部、部分、单个
  • 参数升维

• 更新方向

  • 梯度
  • 海瑟矩阵
  • 次梯度

• 更新方式

  • 叠加惯性
  • 动态学习率

Loss Models

模型（目标函数）在样本整体的损失：度量模型整体预测效果

• 代表模型在整体上的性质，有不同的设计形式

• 可以用于 设计学习策略、评价模型

  • 风险函数
  • 评价函数

• 有时在算法中也会使用整体损失

Expected Risk / Expected Loss / Generalization Loss

期望风险（函数）：损失函数 $L(Y, f(X))$（随机变量）期望

• $P(X, Y)$：随机变量 $(X, Y)$ 遵循的联合分布，未知

• 风险函数值度量模型预测错误程度

  • 反映了学习方法的泛化能力
  • 评价标准（监督学习目标）就应该是选择期望风险最小

• 联合分布未知，所以才需要学习，否则可以直接计算条件分布概率，而计算期望损失需要知道联合分布，因此监督学习是一个病态问题

Empirical Risk / Empirical Loss

经验风险：模型关于给定训练数据集的平均损失

• $\theta$：模型参数
• $D_i$：样本损失权重，常为 $\frac 1 N$，在 Boosting 框架中不同

• 经验风险损失是模型 $f(x)$ 的函数

  • 训练时，模型是模型参数的函数
  • 即其为模型参数函数

• 根据大数定律，样本量容量 $N$ 趋于无穷时，$R{emp}(f)$ 趋于 $R{exp}(f)$

  • 但是现实中训练样本数目有限、很小
  • 利用经验风险估计期望常常并不理想，需要对经验风险进行矫正

• 例子

  • maximum probability estimation：极大似然估计
    • 模型：条件概率分布（贝叶斯生成模型、逻辑回归）
    • 损失函数：对数损失函数

Structual Risk / Structual Loss

结构风险：在经验风险上加上表示 模型复杂度 的 regularizer（penalty term）

• $J(f)$：模型复杂度，定义在假设空间$F$上的泛函
• $\lambda$：权衡经验风险、模型复杂度的系数

• 结构风险最小化
  • 添加 regularization（正则化），调节损失函数（目标函数）
• 模型复杂度 $J(f)$ 表示对复杂模型的惩罚：模型 $f$ 越复杂，复杂项 $J(f)$ 越大
• 案例
  • maximum posterior probability estimation：最大后验概率估计
    • 损失函数：对数损失函数
    • 模型复杂度：模型先验概率对数后取负
    • 先验概率对应模型复杂度，先验概率越小，复杂度越大
  • 岭回归：平方损失 + $L2$ 正则化 $\mathop{\arg\min}{\beta} \sum_{i=1}^N (y_i - f(x_i, \beta))^2 + |\beta|$
  • LASSO：平方损失 + $L1$ 正则化 $\mathop{\arg\min}{\beta} \sum_{i=1}^N (y_i - f(x_i, \beta))^2 + |\beta|_1$

Generalization Ability

泛化能力：方法学习到的模型对未知数据的预测能力，是学习方法本质、重要的性质

• 测试误差衡量学习方法的泛化能力不可靠，其依赖于测试集，而测试集有限
• 学习方法的泛化能力往往是通过研究泛化误差的概率上界进行

Generalization Error Bound

泛化误差上界：泛化误差的 概率 上界

• 是样本容量函数，样本容量增加时，泛化上界趋于 0
• 是假设空间容量函数，假设空间容量越大，模型越难学习，泛化误差上界越大

泛化误差

• 根据 Hoeffding 不等式，泛化误差满足

  $$\begin{align*} & \forall h \in H, & P(|E(h) - \hat E(h)| \geq \epsilon) \leq 2 e^{-2 N \epsilon^2} \\ \Rightarrow & \forall h \in H, & P(|E(h) - \hat E(h)| \leq \epsilon) \geq 1 - 2|H|e^{-2N\epsilon^2} \end{align*}$$

  • $H$：假设空间
  • $N$：样本数量
  • $E(h) := R_{exp}(h)$
  • $\hat E(h) := R_{emp}(h)$

• 证明如下：

  $$\begin{align*} P(\forall h \in H: |E(h) - \hat E(h)| \leq \epsilon|) & = 1 - P(\exists h \in H: |E(h) - \hat E(h)| \geq \epsilon) \\ & = 1 - P((|E(h_1) - \hat E(h_1) \geq \epsilon) \vee \cdots \vee (|E(h_{|H|}) - \hat E_{|H|}| \geq \epsilon)) \\ & \geq 1 - \sum_{i=1}^{|H|} P(|E(h_i) - \hat E(h_i)| \geq \epsilon) \\ & \geq 1 - 2|H|e^{-2N \epsilon^2} \end{align*}$$

• 对任意 $\epsilon$，随样本数量 $m$ 增大， $|E(h) - \hat E(h)| \leq \epsilon$ 概率增大，可以使用经验误差近似泛化误差

二分类泛化误差上界

• 由 Hoeffding 不等式

  $$\begin{align*} P(E(h) - \hat E(h) & \geq \epsilon) \leq exp(-2N\epsilon^2) \\ P(\exists h \in H: E(h) - \hat E(h) \geq \epsilon) & = P(\bigcup_{h \in H} \{ E(h) - \hat E(h) \geq \epsilon \}) \\ & \leq \sum_{h \in H} P(E(h) - \hat E(h) \geq \epsilon) \\ & \leq |H| exp(-2 N \epsilon^2) \end{align*}$$

• 则 $\forall h \in H$，有

  $$P(E(h) - \hat E(h) < \epsilon) \geq 1 - |H| exp(-2 N \epsilon)$$

  则令 $\sigma = |H| exp(-2N\epsilon^2)$，则至少以概率 $1-\sigma$ 满足如下，即得到泛化误差上界

  $$\begin{align*} E(h) & \leq \hat E(h) + \epsilon(|H|, N, \sigma) \\ \epsilon(|H|, N, \sigma) & = \sqrt {\frac 1 {2N} (log |H| + log \frac 1 {\sigma})} \end{align*}$$

Probably Approximate Correct 可学习

PAC 可学习：在短时间内利用少量（多项式级别）样本能够找到假设 $h^{‘}$，满足

• 即需要假设满足两个 PAC 辨识条件

  • 近似条件：泛化误差 $E(h^{‘})$ 足够小
  • 可能正确：满足近似条件概率足够大

• 同等条件下

  • 模型越复杂，泛化误差越大
  • 满足条件的样本数量越大，模型泛化误差越小

• PAC 学习理论关心能否从假设空间 $H$ 中学习到好的假设 $h$

  • 由以上泛化误差可得，取 $\sigma = 2|H|e^{-2N\epsilon^2}$，则样本量满足 $N = \frac {ln \frac {2|H|} \sigma} {2 \epsilon^2}$ 时，模型是 PAC 可学习的

Regularization

正则化：（向目标函数）添加额外信息以求解病态问题、避免过拟合

• 常应用在机器学习、逆问题求解

  • 对模型（目标函数）复杂度惩罚
  • 提高学习模型的泛化能力、避免过拟合
  • 学习简单模型：稀疏模型、引入组结构

• 有多种用途

  • 最小二乘也可以看作是简单的正则化
  • 岭回归中的 $\mathcal{l_2}$ 范数

模型复杂度

模型复杂度：经常作为正则化项添加作为额外信息添加的，衡量模型复杂度方式有很多种

• 函数光滑限制

  • 多项式最高次数

• 向量空间范数

  • $\mathcal{L_0} - norm$：参数个数
  • $\mathcal{L_1} - norm$：参数绝对值和
  • $\mathcal{L_2}$- norm$：参数平方和

$\mathcal{L_0} - norm$

• $\mathcal{l_0} - norm$ 特点
  • 稀疏化约束
  • 解 $\mathcal{L_0}$ 范数正则化是 NP-hard 问题

$\mathcal{L_1} - norm$

• $\mathcal{L_1} - norm$ 特点

  • $\mathcal{L_1}$ 范数可以通过凸松弛得到 $\mathcal{L_0}$ 的近似解
  • 有时候出现解不唯一的情况
  • $\mathcal{L_1}$ 范数凸但不严格可导，可以使用依赖次梯度的方法求解极小化问题

• 应用

  • LASSO

• 求解

  • Proximal Method
  • LARS

$\mathcal{L_2} - norm$

• $\mathcal{L_2} - norm$ 特点
  • 凸且严格可导，极小化问题有解析解

$\mathcal{L_1 + L_2}$

• $\mathcal{L_1 + L_2}$ 特点

  • 有组效应，相关变量权重倾向于相同

• 应用

  • Elastic Net

稀疏解产生

稀疏解：待估参数系数在某些分量上为 0

$\mathcal{L_1} - norm$ 稀疏解的产生

• $\mathcal{L_1}$ 范数在参数满足 一定条件 情况下，能对 平方损失 产生稀疏效果

• 在 $[-1,1]$ 内 $y=|x|$ 导数大于 $y=x^2$（除 0 点）

  • 则特征在 0 点附近内变动时，为了取到极小值，参数必须始终为 0
  • 高阶项在 0 点附近增加速度较慢，所以 $\mathcal{L_1} - norm$ 能产生稀疏解是很广泛的
  • $mathcal{L_1} - norm$ 前系数（权重）越大，能够容许高阶项增加的幅度越大，即压缩能力越强

• 在 0 附近导数 “不小”，即导数在 0 点非 0

  • 对多项式正则化项
    • $\mathcal{L_1} - norm$ 项对稀疏化解起决定性作用
    • 其他项对稀疏解无帮助
  • 对“非多项式”正则化项
    • $e^{|x|}-1$、$ln(|x|+1)$ 等在0点泰勒展开同样得到 $\mathcal{L_1} - norm$ 项
    • 但是此类正则化项难以计算数值，不常用

$\mathcal{L_1} - norm$ 稀疏解推广

• 正负差异化：在正负设置权重不同的 $\mathcal{L_1}$，赋予在正负不同的压缩能力，甚至某侧完全不压缩

• 分段函数压缩：即只要保证在 0 点附近包含 $\mathcal{L_1}$ 用于产生稀疏解，远离 0 处可以设计为常数等不影响精确解的值

  • Smoothly Clipped Absolute Deviation

    $$R(x|\lambda, \gamma) = \left \{ \begin{array} {l} \lambda|x| \qquad & if |x| \leq \lambda \\ \frac {2\gamma\lambda|x| - x^2 - {\lambda}^2 } {2(\gamma - 1)} & if \gamma< |x| <\gamma\lambda \\ \frac { {\lambda}^2(\gamma+1)} 2 & if |x| \geq \gamma\lambda \end{array} \right.$$

  • Derivate of SCAD

    $$R(x; \lambda, \gamma) = \left \{ \begin{array} {l} \lambda \qquad & if |x| \leq \gamma \\ \frac {\gamma\lambda - |x|} {\gamma - 1} & if \lambda < |x| < \gamma\lambda \\ 0 & if |x| \geq \gamma\lambda \end{array} \right.$$

  • Minimax Concave Penalty

    $$R_{\gamma}(x;\lambda) = \left \{ \begin{array} {l} \lambda|x| - \frac {x^2} {2\gamma} \qquad & if |x| \leq \gamma\lambda \\ \frac 1 2 \gamma{\lambda}^2 & if |x| > \gamma\lambda \end{array} \right.$$

• 分指标：对不同指标动态设置 $\mathcal{L_0}$ 系数

  • Adaptive Lasso：$\lambda \sum_J w_jx_j$

稀疏本质

稀疏本质：极值、不光滑，即导数符号突然变化

• 若某约束项导数符号突然变化、其余项在该点处导数为 0，为保证仍然取得极小值，解会聚集（极小）、疏远（极大）该点（类似坡的陡峭程度）

  • 即此类不光滑点会抑制解的变化，不光滑程度即导数变化幅度越大，抑制解变化能力越强，即吸引、排斥解能力越强
  • 容易构造压缩至任意点的约束项
  • 特殊的，不光滑点为 0 时，即得到稀疏解

• 可以设置的多个极小不光滑点，使得解都在不连续集合中

  • 可以使用三角函数、锯齿函数等构造，但此类约束项要起效果，必然会使得目标函数非凸
    • 但是多变量场合，每个变量实际解只会在某个候选解附近，其邻域内仍然是凸的
    • 且锯齿函数这样的突变非凸可能和凸函数具有相当的优秀性质
  • 当这些点均为整数时，这似乎可以近似求解 整数规划

Early Stopping

Early Stopping：提前终止（训练）

• Early Stopping 也可以被视为是 regularizing on time
  • 迭代式训练随着迭代次数增加，往往会有学习复杂模型的倾向
  • 对时间施加正则化，可以减小模型复杂度、提高泛化能力

控制OPs

Neural Network Building Blocks

tf.softmax

tf.Sigmod

tf.ReLU

tf.Convolution2D

tf.MaxPool

Checkpointing

tf.Save

tf.Restore

Queue and Synchronization

tf.Enqueue

tf.Dequeue

tf.MutexAcquire

tf.MutexRelease

Control Flow

tf.count_up_to

tf.cond

pred为True，执行true_fn，否则执行false_fn

1
2
3
4
5

tf.cond(
	pred,
	true_fn=None,
	false_fn =None,
)

tf.case

tf.while_loop

tf.group

tf.Merge

tf.Switch

tf.Enter

tf.Leave

tf.NextIteration

Tensor

张量：n-dimensional array，类型化的多维数组

• TF使用Tensor表示所有的数据
• Tensor包含一个静态类型rank、一个shape
• TF会将python原生类型转换为相应的Tensor
  • 0-d tensor：scalar
  • 1-d tensor：vector，1d-array
  • 2-d tensor：matrix，2d-array

Data Type

• TF被设计为和numpy可以无缝结合

  • TF的变量类型基于numpy变量类型：tf.int32==np.int32
  • bool、numeric等大部分类型可以不加转换的使用TF、np 变量类型
  • TF、np中string类型不完全一样，但TF仍然可以从numpy 中导入string数组，但是不能在numpy中指定类型

• 但尽量使用TF变量类型

  • python原生类型：没有细分类型，TF需要推断类型
  • numpy类型：numpy不兼容GPU，也不能自动计算衍生类型

Constant OPs

tf.constant

1
2
3
4
5
6
7

def constant(
	value,
	dtype=none,
	shape=none,
	name="Const",
	verify_shape=False
)

同值常量OPs

• zeros：类似np中相应函数

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  # `np.zeros` def tf.zeros( shape, dtype=tf.float32, name=None ) # `np.zores_like` def tf.zeros_like( input_tensor, dtype=None, name=None, optimizeTrue )

  • 若没有指明dtype，根据input_tensor确定其中值
    • 对数值型为0.0
    • 对bool型为False
    • 对字符串为b''

• ones：类似np中相应函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# `np.ones`
def tf.ones(
	shape,
	dtype=tf.float32,
	name=None
)

# `np.ones_like`
def tf.ones_like(
	input_tensor,
	dtype=None,
	name=None,
	optimize=True
)


-    若没有指明`dtype`，根据`input_tensor`确定
    -    对数值型为`0.0`
    -    对bool型为`True`
    -    对字符串报错

• fill：以value填充dims给定形状

  1 2 3 4 5 6

  # `np.fill` def tf.fill( dims, value, name=None )

列表常量OPs

• tensor列表不能直接for语句等迭代

• tf.lin_space：start、stop直接均分为num部分

  1 2 3 4 5 6 7

  # `np.linspace` def lin_space( start, stop, num, name=None )

• tf.range：start、stop间等间隔delta取值

  1 2 3 4 5 6 7 8

  # `np.arange` def tf.range( start, limit=None, delta=1, dtype=None, name="range" )

随机常量OPs

• seed：设置随机数种子

  1 2 3

  # np.random.seed def tf.set_random_seed(seed): pass

• random：随机生成函数

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  def tf.random_normal() def tf.truncated_normal( ?avg=0/int/(int), stddev=1.0/float, seed=None/int, name=None ): pass def tf.random_uniform( shape(1d-arr), minval=0, maxval=None, dtype=tf.float32, seed=None/int, name=None/str ): pass def tf.random_crop() def tf.multinomial() def tf.random_gamma()

• shuffle

  1	def tf.random_shuffle()

运算OPs

元素OPs

四则运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def add(x, y, name=None)
def subtract(x, y, name=None)
def sub(x, y, name=None)
def multiply(x, y, name=None)
def mul(x, y, name=None)
	# 加、减、乘

def floordiv(x, y, name=None)
def floor_div(x, y, name=None)
def div(x, y, name=None)
def truncatediv(x, y, name=None)
	# 地板除

def divide(x, y, name=None)
def truediv(x, y, name=None)
	# 浮点除

def realdiv(x, y, name=None)
	# 实数除法，只能用于实数？

def add_n(input, name=None)
	# `input`：list-like，元素shape、type相同
	# 累加`input`中元素的值

逻辑运算

1
2
3

def greater()
def less()
def equal()

数学函数

1
2
3
4
5
6
7
8
9
10
11

def exp()
def log()
def square()
def round()
def sqrt()
def rsqrt()
def pow()
def abs()
def negative()
def sign()
def reciprocal()		# 倒数

列表运算OPs

1
2
3
4
5
6

def tf.Concat()
def tf.Slice()
def tf.Split()
def tf.Rank()
def tf.Shape()
def tf.Shuffle()

矩阵OPs

1
2
3
4

def tf.MatMul()
def tf.MatrixInverse()
def tf.MatrixDeterminant()
def tf.tensordot()				# 矩阵点乘

梯度OPs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

def tf.gradients(				# 求`y`对`[xs]`个元素偏导
	ys: tf.OPs,
	xs: tf.OPs/[tf.OPs],
	grad_ys=None,
	name=None
)
def tf.stop_gradient(
	input,
	name=None
)
def clip_by_value(
	t,
	clip_value_min,
	clip_value_max,
	name=None
)
def tf.clip_by_norm(
	t,
	clip_norm,
	axes=None,
	name=None
)

Variable

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class Variable:
	def __init__(self,
		init_value=None,
		trainable=True,
		collections=None,
		validata_shape=True,
		caching_device=None,
		name=None,
		variable_def=None,
		dtype=None,
		expected_shape=None,
		import_scope=None,
		constraint=None
	)

	# 初始化变量
	# `sess.run`其即初始化变量
	def intializer(self):
		pass

	# 读取变量值
	def value(self):
		pass

	# 获取变量初始化值，其他变量调用、声明依赖该变量
	def initilized_value(self):
		pass

	# 计算、获取变量值，类似`sess.run(OP)`
	def eval(self):
		pass

	# 给变量赋值
	# `assgin`内部有初始化Variable，所以有时可以不用初始化
	def assign(self):
		pass
	#`assgin_add`等依赖于原始值，不会初始化变量
	def assign_add(self, ?dec)
	def assign_divide(self, ?dec)

• Variable是包含很多方法的类

  • 其中方法OPs和一般的OP一样，也需要在Session中执行 才能生效
  • Variable必须在会话中初始化后，才能使用
  • 会话维护自身独立Variable副本，不相互影响

• Variable和图分开存储，甚至是存储在独立参数服务器上

  • 存储大量数据也不会拖慢图载入速度
  • 通常用于存储训练过程中weight、bias、维护图执行过程 中状态信息

• constants是常数OPs

  • 存储在图中：每次载入图会同时被载入，过大的constants 会使得载入图非常慢
  • 所以最好只对原生类型使用constants

Variable创建

tf.get_variable

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def get_variable(
	name,
	shape=None,
	dtype=None,
	initializer=None,
	regularizer=None,
	trainable=True,
	collections=None,
	caching_device=None,
	partitioner=None,
	validate_shape=True,
	use_resource=None,
	custom_getter=None,
	constraint=None
)

• 此封装工厂方法相较于直接通过tf.Variable更好
  • 若变量已设置，可通过变量名获取变量，方便变量共享
  • 可以提供更多的参数定制变量值

1
2
3
4
5
6
7
8
9
10
11

	# `tf.Variable`创建变量
s = tf.Variable(2, name="scalar")
m = tf.Variable([[0,1], [2,3]], name="matrix")
w = tf.Variable(tf.zeros([784, 10]))
	# `tf.get_variable`创建、获取变量
s = tf.get_variable("scalar", initializer=tf.constant(2))
m = tf.get_variable("matrix", initializer=tf.constant([[0,1], [2,3]])
W = tf.get_variable("big_matrix",
	shape=(784, 10),
	initializer=tf.zeros_initializer()
)

Variable初始化

1
2
3
4
5
6
7

with tf.Session() as sess:
	# 初始化所有Variables
	sess.run(tf.global_variable_initialier())
	# 初始化变量子集
	sess.run(tf.variable_initializer([s, m])
	# 初始化指定单个变量
	sess.run(s.initializer)

• 若某Variable依赖其他Variable，需要使用 initialized_value指明依赖，确保依赖线性初始化

  1 2 3

  W = tr.Variable(tf.truncated_normal([700, 100]) # 指明依赖，保证依赖线性初始化 U = tf.Variable(W.initialized_value() * 2)

Session Checkpoint

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class tf.train.Saver:
	def __init__(self,
		var_list=None/list/dict,
		reshape=False,
		sharded=False,
		max_to_keep=5,
		keep_checkpoint_every_n_hours=10000.0,
		name=None,
		restore_sequentially=False,
		saver_def=None,
		builder=None,
		defer_build=False,
		allow_empty=False,
		write_version=tf.train.SaverDef.V2,
		pad_step_number=False,
		save_relative_paths=False,
		filename=None
	):
		self.last_checkpoints

• 用途：保存Session中变量（张量值），将变量名映射至张量值

• 参数

  • var_list：待保存、恢复变量，缺省所有
    • 变量需在tf.train.Saver实例化前创建
  • reshape：允许恢复并重新设定张量形状
  • sharded：碎片化保存至多个设备
  • max_to_keep：最多保存checkpoint数目
  • keep_checkpoint_every_n_hours：checkpoint有效时间
  • restore_sequentially：各设备中顺序恢复变量，可以 减少内存消耗

• 成员

  • last_checkpoints：最近保存checkpoints

保存Session

1
2
3
4
5
6
7
8
9
10

def Saver.save(self,
	sess,
	save_path,
	global_step=None/str,
	latest_filename=None("checkpoint")/str,
	meta_graph_suffix="meta",
	write_meta_graph=True,
	write_state=True
) -> str(path):
	pass

• 用途：保存Session，要求变量已初始化

• 参数

  • global_step：添加至save_path以区别不同步骤
  • latest_filename：checkpoint文件名
  • meta_graph_suffix：MetaGraphDef文件名后缀

恢复Session

1
2

def Saver.restore(sess, save_path(str)):
	pass

• 用途：从save_path指明的路径中恢复模型

• 模型路径可以通过Saver.last_checkpoints属性、 tf.train.get_checkpoint_state()函数获得

tf.train.get_checkpoint_state

1
2
3
4
5

def tf.train.get_checkpoint_state(
	checkpoint_dir(str),
	latest_filename=None
):
	pass

• 用途：获取指定checkpoint目录下checkpoint状态
  • 需要图结构已经建好、Session开启
  • 恢复模型得到的变量无需初始化

1
2
3

ckpt = tf.train.get_checkpoint_state(checkpoint_dir)
saver.restore(ckpt.model_checkpoint_path)
saver.restore(ckpt.all_model_checkpoint_paths[-1])

Graph Saver

tf.train.write_graph

1
2
3
4
5
6

def tf.train.write_graph(
	graph_or_graph_def: tf.Graph,
	logdir: str,
	name: str,
	as_text=True
)

• 用途：存储图至文件中

• 参数

  • as_text：以ASCII方式写入文件

Summary Saver

tf.summary.FileWriter

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class tf.summary.FileWriter:
	def __init__(self,
		?path=str,
		graph=tf.Graph
	)

	# 添加summary记录
	def add_summary(self,
		summary: OP,
		global_step
	):
		pass

	# 关闭`log`记录
	def close(self):
		pass

• 用途：创建FileWriter对象用于记录log

  • 存储图到文件夹中，文件名由TF自行生成
  • 可通过TensorBoard组件查看生成的event log文件

• 说明

  • 一般在图定义完成后、Session执行前创建FileWriter 对象，Session结束后关闭

实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

 # 创建自定义summary
with tf.name_scope("summaries"):
	tf.summary.scalar("loss", self.loss)
	tf.summary.scalar("accuracy", self.accuracy)
	tf.summary.histogram("histogram loss", self.loss)
	summary_op = tf.summary.merge_all()

saver = tf.train.Saver()

with tf.Session() as sess:
	sess.run(tf.global_variables_initializer())

	# 从checkpoint中恢复Session
	ckpt = tf.train.get_check_state(os.path.dirname("checkpoint_dir"))
	if ckpt and ckpt.model_check_path:
		saver.restore(sess, ckpt.mode_checkpoint_path)

	# summary存储图
	writer = tf.summary.FileWriter("./graphs", sess.graph)
	for index in range(10000):
		loas_batch, _, summary = session.run([loss, optimizer, summary_op])
		writer.add_summary(summary, global_step=index)

		if (index + 1) % 1000 = 0:
			saver.save(sess, "checkpoint_dir", index)

 # 关闭`FileWriter`，生成event log文件
write.close()

Optimizer

1
2
3
4
5
6
7
8
9
10
11

class tf.train.GradientDescentOptimizer:

class tf.train.AdagradOptimizer:

class tf.train.MomentumOptimizer:

class tf.train.AdamOptimizer:

class tf.train.FtrlOptimizer:

class tf.train.RMSPropOptmizer:

Session

Session：TF中OPs对象执行、Tensor对象计算的封装环境

• Session管理图、OPs

  • 所有图必须Session中执行
  • 将图中OPs、其执行方法分发到CPU、GPU、TPU等设备上
  • 为当前变量值分配内存

• Session只执行Data/Tensor Flow中OPs，忽略不相关节点

  • 即通往fetches的flow中的OPs构成子图才会被计算

• 各Session中各值独立维护，不会相互影响

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Session:
	def __init__(self,
		target=str,
		graph=None/tf.Graph,
		config=None/tf.ConfigProto)

		# 获取Session中载入图
		self.graph

	# 关闭会话，释放资源
	def close(self):
		pass

	# 支持上下文语法
	def __enter__(self):
		pass
	def __exit__(self):
		pass

	# 执行TensorFlow中节点，获取`fetches`中节点值
	# 返回值若为Tensor
		# python中：以`np.ndarray`返回
		# C++/C中：以`tensorflow:Tensor`返回
	# 可直接调用`.eval()`获得单个OP值
	def run(self,
		fetches=tf.OPs/[tf.OPs],
		feed_dict=None/dict,
		options=None,
		run_metadata=None)

tf.InteractiveSession

tf.InteractiveSession：开启交互式会话

1
2
3
4
5
6
7
8
9
10
11

 # 开启交互式Session
sess = tf.InteractiveSession()
a = tf.constant(5.0)
b = tf.constant(6.0)
c = a * b
x = tf.Variable([1.0, 2.0])
 # 无需显式在`sess.run`中执行
 # 直接调用`OPs.eval/run()`方法得到结果
x.initializer.run()
print(c.eval())
sess.close()

Session执行

• Fetch机制：sess.run()执行图时，传入需取回的结果， 取回操作输出内容

• Feed机制：通过feed_dict参数，使用自定义tensor值替代图 中任意feeable OPs的输出

  • tf.placeholder()表示创建占位符，执行Graph时必须 使用tensor替代
  • feed_dict只是函数参数，只在调用它的方法内有效， 方法执行完毕则消失

• 可以通过feed_dict feed所有feedable tensor，placeholder 只是指明必须给某些提供值

  1 2 3 4

  a = tf.add(2, 5) b = tf.multiply(a, 3) with tf.Session() as sess: sess.run(b, feed_dict={a: 15}) # 45

config参数选项

• log_device_placement：打印每个操作所用设备
• allow_soft_placement：允许不在GPU上执行操作自动迁移到 CPU上执行
• gpu_options
  • allow_growth：按需分配显存
  • per_process_gpu_memory_fraction：指定每个GPU进程 使用显存比例（无法对单个GPU分别设置）

• 具体配置参见tf.ConfigProto

Graph

Graph：表示TF中计算任务，

• operation/node：Graph中节点，包括：operator、 variable、constant

  • 获取一个、多个Tensor执行计算、产生、返回tensor
  • 不能无法对其值直接进行访问、比较、操作
  • 图中节点可以命名，TF会自动给未命名节点命名

• tensor：Graph中边，n维数组

  • TF中所有对象都是Operators
  • tensor是OPs执行结果，在图中传递/流动

• 图计算模型优势

  • 优化能力强、节省计算资源
    • 缓冲自动重用
    • 常量折叠，只计算取得目标值过程中必须计算的值
    • 方便并行化
    • 自动权衡计算、存储效率
  • 易于部署
    • 可被割成子图（即极大连通分量），便于自动区分
    • 子图可以分发到不同的设备上分布式执行，即模型并行
    • 许多通用ML模型是通过有向图教学、可视化的

• 图计算模型劣势

  • 难以debug
    • 图定义之后执行才会报错
    • 无法通过pdb、打印状态debug
  • 语法繁复

构建图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Graph:
	def __init__(self):
		pass

	# 将当前图作为默认图
	# 支持上下文语法
	def as_default(self):
		pass

	# 强制OPs依赖关系（图中未反映），即优先执行指定OPs
	# 支持上下文语法
	def as_default(self):
	def control_dependencies(self,
		?ops=[tf.OPs])
		pass

	# 以ProtoBuf格式展示Graph
	def as_graph_def(self):
		pass

	# 判断图中节点是否可以被feed
	def is_feedable(self,
		?op=tf.OPs):
		pass

• 可以通过tf.Graph创建新图，但最好在是在一张图中使用多个 不相连的子图，而不是多张图

  • 充分性：Session执行图时忽略不必要的OPs
  • 必要性
    • 多张图需要多个会话，每张图执行时默认尝试使用所有 可能资源
    • 不能通过python/numpy在图间传递数据（分布式系统）

• 初始化即包含默认图，OP构造器默认为其增加节点

  • 通过tf.get_default_graph()获取

图相关方法

• 获取TF初始化的默认图

  1 2	def tf.get_default_graph(): pass

命名空间

1
2
3
4
5
6
7
8

 # 均支持、利用上下文语法，将OPs定义于其下
def tf.name_scope(name(str)):
	pass
def tf.variable_scope(
	name(str),
	reuse=tf.AUTO_REUSE
):
	pass

• tf.name_scope：将变量分组
  • 只是将变量打包，不影响变量的重用、可见性等
  • 方便管理、查看graph
• tf.variable_scope：
  • 对变量有控制能力
    • 可设置变量重用性
    • 变量可见性局限于该variable scope内，即不同 variable scope间可以有完全同名变量 （未被TF添加顺序后缀）
  • 会隐式创建name scope
  • 大部分情况是用于实现变量共享

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

def fully_connected(x, output_dim, scope):
	# 设置variable scope中变量自动重用
	# 或者调用`scope.reuse_variables()`声明变量可重用
	with tf.variable_scope(scope, reuse=tf.AUTO_REUSE) as scope:
		# 在当前variable scope中获取、创建变量
		w = tf.get_variable("weights", [x.shape[1]], output_dim,
							initializer=tf.random_normal_initializer())
		b = tf.get_variable("biases", [output_dim],
							initializer=tf.constant_initizer(0.0))
		return tf.matmul(x, w) + b

def two_hidden_layers(x):
	h1 = fully_connected(x, 50, "h1")
	h2 =-fully_connected(h1, 10, "h2")

with tf.variable_scope("two_layers") as scope:
	logits1 = two_hidden_layers(x1)
	logits2 = two_hidden_layers(x2)

Lazy Loading

Lazy Loading：推迟声明/初始化OP对象至载入图时 （不是指TF的延迟计算，是个人代码结构问题，虽然是TF延迟图计算 模型的结果）

• 延迟加载容易导致向图中添加大量重复节点，影响图的载入、 传递

  1 2 3 4 5 6 7 8 9 10 11

  x = tf.Variable(10, name='x') y = tf.Variable(20, name='y') with tf.Session() as sess: sess.run(tf.global_variables_initializer()) writer = tf.summary.FileWriter('graphs/lazy_loading', sess.graph) for _ in range(10): # 延迟加载节点，每次执行都会添加`tf.add`OP sess.run(tf.add(x, y)) print(tf.get_default_graph().as_graph_def()) writer.close()

• 解决方案

  • 总是把（图的搭建）OPs的定义、执行分开
  • python利用@property装饰器，使用单例模式函数 封装变量控制，保证仅首次调用函数时才创建OP

Eager Execution

1
2
3
4

import tensorflow as tf
import tensorflow.contrib.eager as tfe
 # 启用TF eager execution
tfe.enable_eager_execution()

• 优势

  • 支持python debug工具
  • 提供实时报错
  • 支持python数据结构

  • 支持pythonic的控制流

    1 2 3

    i = tf.constant(0) whlile i < 1000: i = tf.add(i, 1)

• eager execution开启后

  • tensors行为类似np.ndarray
  • 大部分API和未开启同样工作，倾向于使用
    • tfe.Variable
    • tf.contrib.summary
    • tfe.Iterator
    • tfe.py_func
    • 面向对象的layers
    • 需要自行管理变量存储

• eager execution和graph大部分兼容

  • checkpoint兼容
  • 代码可以同时用于python过程、构建图
  • 可使用@tfe.function将计算编译为图

示例

• placeholder、sessions

  1 2 3 4 5 6 7 8 9

  # 普通TF x = tf.placholder(tf.float32, shape=[1, 1]) m = tf.matmul(x, x) with tf.Session() as sess: m_out = sess.run(m, feed_dict={x: [[2.]]}) # Eager Execution x = [[2.]] m = tf.matmul(x, x)

• Lazy loading

  1 2 3 4 5

  x = tf.random_uniform([2, 2]) for i in range(x.shape[0]): for j in range(x.shape[1]): # 不会添加多个节点 print(x[i, j])

Device

设备标识

• 设备标识：设备使用字符串进行标识

  • /cpu:0：所有CPU都以此作为名称
  • /gpu:0：第一个GPU，如果有
  • /gpu:1：第二个GPU

  1 2 3 4 5 6

  # 为计算指定硬件资源 with tf.device("/gpu:2"): a = tf.constant([1.0, 2.0, 3.0, 4.0, 5.0], name="a") b = tf.constant([1.0, 2.0, 3.0, 4.0, 5.0], name="b") c = tf.multiply(a, b) # creates a graph

• 环境变量：python中既可以修改os.environ，也可以直接设置 中设置环境变量

  • CUDA_VISIBLE_DEVICES：可被使用的GPU id

设备执行

设备执行：TF将图形定义转换成分布式执行的操作以充分利用计算 资源

• TF默认自动检测硬件配置，尽可能使用找到首个GPU执行操作

• TF会默认占用所有GPU及每个GPU的所有显存（可配置）

  • 但只有一个GPU参与计算，其他GPU默认不参与计算（显存 仍然被占用），需要明确将OPs指派给其执行
  • 指派GPU数量需通过设置环境变量实现
  • 控制显存占用需设置Session config参数

• 注意：有些操作不能再GPU上完成，手动指派计算设备需要注意

tf.ConfigProto

• Session参数配置

  1 2 3 4 5

  # `tf.ConfigProto`配置方法 conf = tf.ConfigProto(log_device_placement=True) conf.gpu_options.allow_growth=True sess = tf.Session(config=conf) sess.close()

评估方向

模型误差

• 给定损失函数时，基于损失函数的误差显然评估学习方法的标准

• 回归预测模型：模型误差主要使用 MSE
• 分类预测模型：模型误差主要是分类错误率 ERR=1-ACC

• 模型训练时采用损失函数不一定是评估时使用的

Training Error

训练误差：模型在训练集上的误差，损失函数 $L(Y, F(X))$ 均值

• $\hat f$：学习到的模型
• $N$：训练样本容量

• 训练时采用的损失函数和评估时一致时，训练误差等于经验风险
• 训练误差对盘对给定问题是否容易学习是有意义的，但是本质上不重要
  • 模型训练本身就以最小化训练误差为标准，如：最小化 MSE、最大化预测准确率，一般偏低，不能作为模型预测误差的估计
  • 训练误差随模型复杂度增加单调下降（不考虑模型中随机因素）

Test Error

测试误差：模型在测试集上的误差，损失函数 $L(Y, f(X))$ 均值

• $\hat f$：学习到的模型
• $N$：测试样本容量

• 测试误差反映了学习方法对未知测试数据集的预测能力，是模型 generalization ability 的度量，可以作为模型误差估计

• 测试误差随模型复杂度增加呈U型

  • 偏差降低程度大于方差增加程度，测试误差降低
  • 偏差降低程度小于方差增加程度，测试误差增大
• 训练误差小但测试误差大表明模型过拟合，使测试误差最小的模型为理想模型

模型复杂度

• approximation error：近似误差，模型偏差，代表模型对训练集的拟合程度
• estimation error：估计误差，模型方差，代表模型对训练集波动的稳健性

• 模型复杂度越高

  • 低偏差：对训练集的拟合充分
  • 高方差：模型紧跟特定数据点，受其影响较大，预测结果不稳定
  • 远离真实关系，模型在来自同系统中其他尚未观测的数据集上预测误差大

• 而训练集、测试集往往不完全相同

  • 复杂度较高的模型（过拟合）在测试集上往往由于其高方差效果不好，而建立模型最终目的是用于预测未知数据
  • 所以要兼顾偏差和方差，通过不同建模策略，找到恰当模型，其复杂度不太大且误差在可接受的水平
  • 使得模型更贴近真实关系，泛化能力较好

• 简单模型：低方差高偏差

• 复杂模型：低偏差高方差

• 模型复杂度衡量参data_science/loss

Over-Fitting

过拟合：学习时选择的所包含的模型复杂度大（参数过多），导致模型对已知数据预测很好，对未知数据预测效果很差

• 若在假设空间中存在“真模型”，则选择的模型应该逼近真模型（参数个数相近）
• 一味追求对训练集的预测能力，复杂度往往会比“真模型”更高

解决方法

• 减少预测变量数量
  • 最优子集回归：选择合适评价函数（带罚）选择最优模型
  • 验证集挑选模型：将训练集使用 抽样技术 分出部分作为 validation set，使用额外验证集挑选使得损失最小的模型
  • 正则化（罚、结构化风险最小策略）
    • 岭回归：平方损失，$L_2$ 范数
    • LASSO：绝对值损失，$L_1$ 范数
    • Elastic Net
• 减弱变量特化程度：仅适合迭代求参数的方法
  • EarlyStop：提前终止模型训练
  • Dropout：每次训练部分神经元

模型信息来源

• 训练数据包含信息
• 模型形成过程中提供的先验信息
  • 模型：采用特定内在结构（如深度学习不同网络结构）、条件假设、其他约束条件（正则项）
  • 数据：调整、变换、扩展训练数据，让其展现更多、更有用的信息

评价指标

• Classification 分类问题：输出变量$Y$为有限个离散变量

  • 混淆矩阵
    • F-Measure
    • TPR、FPR
  • ROC
  • AUC

• Tagging 标注问题：输入 $X^{(1)}, X^{(2)}, \cdots, X^{(n)}$、输出 $Y^{(1)}, Y^{(2)}, \cdots, Y^{(n)}$ 均为变量序列

  • 类似分类问题

• Regression 回归问题

  • Squared Error
    • MSE
    • $R^2$、$R^2_{Adj}$
    • AIC
    • BIC
  • Absolute Error
    • MAE
    • MAPE
    • SMAPE

• 经验损失、结构损失总是能用作评价模型，但是意义不明确

逻辑斯蒂回归

逻辑斯蒂分布

• $\mu$：位置参数
• $\gamma$：形状参数

• 分布函数属于逻辑斯蒂函数

• 分布函数图像为sigmoid curve

  • 关于的$(\mu, \frac 1 2)$中心对称 $$F(-x+\mu) - \frac 1 2 = -F(x+\mu) + \frac 1 2$$
  • 曲线在靠近$\mu$中心附近增长速度快，两端速度增长慢
  • 形状参数$\gamma$越小，曲线在中心附近增加越快

• 模型优点

  • 模型输出值位于0、1之间，天然具有概率意义，方便观测 样本概率分数
  • 可以结合$l-norm$正则化解决过拟合、共线性问题
  • 实现简单，广泛用于工业问题
  • 分类时计算量比较小、速度快、消耗资源少

• 模型缺点

  • 特征空间很大时，性能不是很好，容易欠拟合，准确率一般
  • 对非线性特征需要进行转换

Binomial Logistic Regression Model

二项逻辑斯蒂回归模型：形式为参数化逻辑斯蒂分布的二分类 生成模型

• $w, b$：权值向量、偏置
• $\hat x = (x^T|1)^T$
• $\hat w = (w^T|b)^T$

• 逻辑回归比较两个条件概率值，将实例$x$归于条件概率较大类

• 通过逻辑回归模型，可以将线性函数$wx$转换为概率

  • 线性函数值越接近正无穷，概率值越接近1
  • 线性函数值越接近负无穷，概率值越接近0

Odds/Odds Ratio

• 在逻辑回归模型中，输出$Y=1$的对数几率是输入x的线性函数

  $$log \frac {P(Y=1|x)} {1-P(Y=1|x)} = \hat w \hat x$$

• OR在逻辑回归中意义：$x_i$每增加一个单位，odds将变为原来 的$e^{w_i}$倍

  $$\begin{align*} odd &= \frac {P(Y=1|x)} {1-P(Y=1|x)} = e^{\hat w \hat x} \\ OR_{x_i+1 / x_i} &= e^{w_i} \end{align*}$$

  • 对数值型变量

    • 多元LR中，变量对应的系数可以计算相应 Conditional OR
    • 可以建立单变量LR，得到变量系数及相应 Marginal OR

  • 对分类型变量

    • 可以直接计算变量各取值间对应的OR
    • 变量数值化编码建立模型，得到变量对应OR

    • 根据变量编码方式不同，变量对应OR的含义不同，其中 符合数值变量变动模式的是WOE线性编码

策略

极大似然：极小对数损失（交叉熵损失）

• $\pi(x) = P(Y=1|x)$

算法

• 通常采用梯度下降、拟牛顿法求解有以上最优化问题

Multi-Nominal Logistic Regression Model

多项逻辑斯蒂回归：二项逻辑回归模型推广

• 策略、算法类似二项逻辑回归模型

Generalized Linear Model

todo

Maximum Entropy Model

最大熵原理

最大熵原理：学习概率模型时，在所有可能的概率模型（分布）中， 熵最大的模型是最好的模型

• 使用约束条件确定概率模型的集合，则最大熵原理也可以表述为 在满足约束条件的模型中选取熵最大的模型

• 直观的，最大熵原理认为

  • 概率模型要满足已有事实（约束条件）
  • 没有更多信息的情况下，不确定部分是等可能的
  • 等可能不容易操作，所有考虑使用可优化的熵最大化 表示等可能性

最大熵模型

最大熵模型为生成模型

• 对给定数据集$T={(x_1,y_1),\cdots,(x_N,y_N)}$，联合分布 P(X,Y)、边缘分布P(X)的经验分布如下

  $$\begin{align*} \tilde P(X=x, Y=y) & = \frac {v(X=x, Y=y)} N \\ \tilde P(X=x) & = \frac {v(X=x)} N \end{align*}$$

  • $v(X=x,Y=y)$：训练集中样本$(x,y)$出频数

• 用如下feature function $f(x, y)$描述输入x、输出y之间 某个事实

  $$f(x, y) = \left \{ \begin{array}{l} 1, & x、y满足某一事实 \\ 0, & 否则 \end{array} \right.$$

  • 特征函数关于经验分布$\tilde P(X, Y)$的期望

    $$E_{\tilde P} = \sum_{x,y} \tilde P(x,y)f(x,y)$$

  • 特征函数关于生成模型$P(Y|X)$、经验分布$\tilde P(X)$ 期望

    $$E_P(f(x)) = \sum_{x,y} \tilde P(x)P(y|x)f(x,y)$$

• 期望模型$P(Y|X)$能够获取数据中信息，则两个期望值应该相等

  $$\begin{align*} E_P(f) & = E_{\tilde P}(f) \\ \sum_{x,y} \tilde P(x)P(y|x)f(x,y) & = \sum_{x,y} \tilde P(x,y)f(x,y) \end{align*}$$

  此即作为模型学习的约束条件

  • 此约束是纯粹的关于$P(Y|X)$的约束，只是约束形式特殊， 需要通过期望关联熵

  • 若有其他表述形式、可以直接带入的、关于$P(Y|X)$约束， 可以直接使用

• 满足所有约束条件的模型集合为 $$\mathcal{C} = \{P | E_{P(f_i)} = E_{\tilde P (f_i)}, i=1,2,\cdots,n \}$$ 定义在条件概率分布$P(Y|X)$上的条件熵为 $$H(P) = -\sum_{x,y} \tilde P(x) P(y|x) logP(y|x)$$ 则模型集合$\mathcal{C}$中条件熵最大者即为最大是模型

策略

最大熵模型的策略为以下约束最优化问题

• 引入拉格朗日函数

  $$\begin{align*} L(P, w) & = -H(P) - w_0(1-\sum_y P(y|x)) + \sum_{m=1}^M w_m(E_{\tilde P}(f_i) - E_P(f_i)) \\ & = \sum_{x,y} \tilde P(x) P(y|x) logP(y|x) + w_0 (1-\sum_y P(y|x)) + \sum_{m=1}^M w_m (\sum_{x,y} \tilde P(x,y)f_i(x, y) - \tilde P(x)P(y|x)f_i(x,y)) \end{align*}$$

  • 原始问题为

    $$\min_{P \in \mathcal{C}} \max_{w} L(P, w)$$

  • 对偶问题为

    $$\max_{w} \min_{P \in \mathcal{C}} L(P, w)$$

  • 考虑拉格朗日函数$L(P, w)$是P的凸函数，则原始问题、 对偶问题解相同

• 记

  $$\begin{align*} \Psi(w) & = \min_{P \in \mathcal{C}} L(P, w) = L(P_w, w) \\ P_w & = \arg\min_{P \in \mathcal{C}} L(P, w) = P_w(Y|X) \end{align*}$$

• 求$L(P, w)$对$P(Y|X)$偏导

  $$\begin{align*} \frac {\partial L(P, w)} {\partial P(Y|X)} & = \sum_{x,y} \tilde P(x)(logP(y|x)+1) - \sum_y w_0 - \sum_{x,y}(\tilde P(x) \sum_{i=1}^N w_i f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x)(log P(y|x) + 1 - w_0 - \sum_{i=1}^N w_i f_i(x, y)) \end{align*}$$

  偏导置0，考虑到$\tilde P(x) > 0$，其系数必始终为0，有

  $$\begin{align*} P(Y|X) & = \exp(\sum_{i=1}^N w_i f_i(x,y) + w_0 - 1) \\ & = \frac {exp(\sum_{i=1}^N w_i f_i(x,y))} {exp(1-w_0)} \end{align*}$$

• 考虑到约束$\sum_y P(y|x) = 1$，有

  $$\begin{align*} P_w(y|x) & = \frac 1 {Z_w(x)} exp(\sum_{i=1}^N w_i f_i(x,y)) \\ Z_w(x) & = \sum_y exp(\sum_{i=1}^N w_i f_i(x,y)) \\ & = exp(1 - w_0) \end{align*}$$

  • $Z_w(x)$：规范化因子
  • $f(x, y)$：特征
  • $w_i$：特征权值

• 原最优化问题等价于求解偶问题极大化问题$\max_w \Psi(w)$

  $$\begin{align*} \Psi(w) & = \sum_{x,y} \tilde P(x) P_w(y|x) logP_w(y|x) + \sum_{i=1}^N w_i(\sum_{x,y} \tilde P(x,y) f_i(x,y) - \sum_{x,y} \tilde P(x) P_w(y|x) f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) + \sum_{x,y} \tilde P(x,y) P_w(y|x)(log P_w(y|x) - \sum_{i=1}^N w_i f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_{x,y} \tilde P(x,y) P_w(y|x) log Z_w(x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_x \tilde P(x) log Z_w(x) \end{align*}$$

  记其解为

  $$w^{*} = \arg\max_w \Psi(w)$$

  带入即可得到最优（最大熵）模型$P_{w^{*}}(Y|X)$

策略性质

• 已知训练数据的经验概率分布为$\tilde P(X,Y)$，则条件概率 分布$P(Y|X)$的对数似然函数为

  $$\begin{align*} L_{\tilde P}(P_w) & = N log \prod_{x,y} P(y|x)^{\tilde P(x,y)} \\ & = \sum_{x,y} N * \tilde P(x,y) log P(y|x) \end{align*}$$

  • 这里省略了系数样本数量$N$

• 将最大熵模型带入，可得

  $$\begin{align*} L_{\tilde P_w} & = \sum_{x,y} \tilde P(y|x) logP(y|x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_{x,y} \tilde P(x,y)log Z_w(x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_x \tilde P(x) log Z_w(x) \\ & = \Psi(w) \end{align*}$$

  对偶函数$\Psi(w)$等价于对数似然函数$L_{\tilde P}(P_w)$， 即最大熵模型中，对偶函数极大等价于模型极大似然估计

改进的迭代尺度法

• 思想

  • 假设最大熵模型当前参数向量$w=(w_1,w_2,\cdots,w_M)^T$
  • 希望能找到新的参数向量（参数向量更新） $w+\sigma=(w_1+\sigma_1,\cdots,w_M+\sigma_M)$ 使得模型对数似然函数/对偶函数值增加
  • 不断对似然函数值进行更新，直到找到对数似然函数极大值

• 对给定经验分布$\tilde P(x,y)$，参数向量更新至$w+\sigma$ 时，对数似然函数值变化为

  $$\begin{align*} L(w+\sigma) - L(w) & = \sum_{x,y} \tilde P(x,y) log P_{w+\sigma}(y|x) - \sum_{x,y} \tilde P(x,y) log P_w(y|x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) - \sum_x \tilde P(x) log \frac {Z_{w+\sigma}(x)} {Z_w(x)} \\ & \geq \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \frac {Z_{w+\sigma}(x)} {Z_w(x)} \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_y(y|x) exp(\sum_{i=1}^M \sigma_i f_i(x,y)) \end{align*}$$

  • 不等式步利用$a - 1 \geq log a, a \geq 1$

  • 最后一步利用

    $$\begin{align*} \frac {Z_{w+\sigma}(x)} {Z_w(x)} & = \frac 1 {Z_w(x)} \sum_y exp(\sum_{i=1}^M (w_i + \sigma_i) f_i(x, y)) \\ & = \frac 1 {Z_w(x)} \sum_y exp(\sum_{i=1}^M w_i f_i(x,y) + \sigma_i f_i(x,y)) \\ & = \sum_y P_w(y|x) exp(\sum_{i=1}^n \sigma_i f_i(x,y)) \end{align*}$$

• 记上式右端为$A(\sigma|w)$，则其为对数似然函数改变量的 一个下界

  $$L(w+\sigma) - L(w) \geq A(\sigma|w)$$
  • 若适当的$\sigma$能增加其值，则对数似然函数值也应该 增加
  • 函数$A(\sigma|w)$中因变量$\sigma$为向量，难以同时 优化，尝试每次只优化一个变量$\sigma_i$，固定其他变量 $\sigma_j$

• 记

  $$f^{**} (x,y) = \sum_i f_i(x,y)$$

  考虑到$f_i(x,y)$为二值函数，则$f^{**}(x,y)$表示所有特征 在$(x,y)$出现的次数，且有

  $$A(\sigma|w) = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_w(y|x) exp(f^{**}(x,y) \sum_{i=1}^M \frac {\sigma_i f_i(x,y)} {f^{**}(x,y)})$$

• 考虑到$\sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} = 1$， 由指数函数凸性、Jensen不等式有

  $$exp(\sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} \sigma_i f^{**}(x,y)) \leq \sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} exp(\sigma_i f^{**}(x,y))$$

  则

  $$A(\sigma|w) \geq \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_w(y|x) \sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} exp(\sigma_i f^{**}(x,y))$$

• 记上述不等式右端为$B(\sigma|w)$，则有

  $$L(w+\sigma) - L(w) \geq B(\sigma|w)$$

  其为对数似然函数改变量的一个新、相对不紧的下界

• 求$B(\sigma|w)$对$\sigma_i$的偏导

  $$\frac {\partial B(\sigma|w)} {\partial \sigma_i} = \sum_{x,y} \tilde P(x,y) f_i(x,y) - \sum_x \tilde P(x) \sum_y P_w(y|x) f_i(x,y) exp(\sigma_i f^{**}(x,y))$$

  置偏导为0，可得

  $$\sum_x \tilde P(x) \sum_y P_w(y|x) f_i(x,y) exp(\sigma_i f^{**}(x,y)) = \sum_{x,y} \tilde P(x,y) f_i(x,y) = E_{\tilde P}(f_i)$$

  其中仅含变量$\sigma_i$，则依次求解以上方程即可得到 $\sigma$

算法

• 输入：特征函数$f_1, f_2, \cdots, f_M$、经验分布 $\tilde P(x)$、最大熵模型$P_w(x)$
• 输出：最优参数值$wi^{*}$、最优模型$P{w^{*}}$

1. 对所有$i \in {1,2,\cdots,M}$，取初值$w_i = 0$

2. 对每个$i \in {1,2,\cdots,M}$，求解以上方程得$\sigma_i$

   • 若$f^{**}(x,y)=C$为常数，则$\sigma_i$有解析解

     $$\sigma_i = \frac 1 C log \frac {E_{\tilde P}(f_i)} {E_P(f_i)}$$

   • 若$f^{**}(x,y)$不是常数，则可以通过牛顿法迭代求解

     $$\sigma_i^{(k+1)} = \sigma_i^{(k)} - \frac {g(\sigma_i^{(k)})} {g^{'}(\sigma_i^{(k)})}$$

     • $g(\sigma_i)$：上述方程对应函数

     • 上述方程有单根，选择适当初值则牛顿法恒收敛

3. 更新$w_i$，$w_i \leftarrow w_i + \sigma_i$，若不是所有 $w_i$均收敛，重复2

BFGS算法

对最大熵模型

• 为方便，目标函数改为求极小

  $$\begin{array}{l} \min_{w \in R^M} f(w) = \sum_x \tilde P(x) log \sum_{y} exp(\sum_{i=1}^M w_i f_i(x,y)) - \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M w_i f_i(x,y) \end{array}$$

• 梯度为

  $$\begin{align*} g(w) & = (\frac {\partial f(w)} {\partial w_i}, \cdots, \frac {\partial f(w)} {\partial w_M})^T \\ \frac {\partial f(w)} {\partial w_M} & = \sum_{x,y} \tilde P(x) P_w(y|x) f_i(x,y) - E_{\tilde P}(f_i) \end{align*}$$

算法

将目标函数带入BFGS算法即可

• 输入：特征函数$f_1, f_2, \cdots, f_M$、经验分布 $\tilde P(x)$、最大熵模型$P_w(x)$
• 输出：最优参数值$wi^{*}$、最优模型$P{w^{*}}$

1. 取初值$w^{(0)}$、正定对称矩阵$B^{(0)}$，置k=0

2. 计算$g^{(k)} = g(w^{(k)})$，若$|g^{(k)}| < \epsilon$， 停止计算，得到解$w^{*} = w^{(k)}$

3. 由拟牛顿公式$B^{(k)}p^{(k)} = -g^{(k)}$求解$p^{(k)}$

4. 一维搜索，求解

   $$\lambda^{(k)} = \arg\min_{\lambda} f(w^{(k)} + \lambda p_k)$$

5. 置$w^{(k+1)} = w^{(k)} + \lambda^{(k)} p_k$

6. 计算$g^{(k+1)} = g(w^{(k+1)})$，若 $|g^{(k+1)}| < \epsilon$，停止计算，得到解 $w^{*} = w^{(k+1)}$，否则求

   $$B^{(k+1)} = B^{(k)} - \frac {B^{(k)} s^{(k)} (s^{(k)})^T B^{(k)}} {(s^{(k)})^T B^{(k)} s^{(k)}} + \frac {y^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}}$$

   • $s^{(k)} = w^{(k+1)} - w^{(k)}$
   • $y^{(k)} = g^{(k+1)} - g^{(k)}$

7. 置k=k+1，转3