Long Short Term Memory

LSTM：通过刻意设计、默认可以学习长期依赖信息的RNN网络

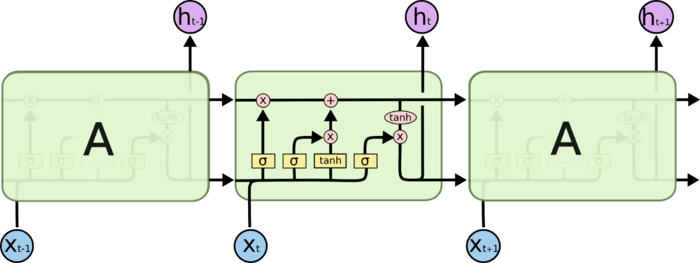
• LSTM中每个重复的模块（层）称为细胞

  • 细胞结构经过特殊设计，相较于准RNN简单细胞结构能较好 保留长时信息

• 多个LSTM细胞可以组成block，其中细胞门权值共享

  • block中各个细胞状态不同
  • 这个是同时刻、不同层的真权值共享，类似CNN中的卷积核
  • 减少参数个数，效率更高

• long term memory：长期记忆，参数
• short term memory：短期记忆，数据流
• long short term memory：长[的]短期记忆，细胞状态

LSTM标准细胞结构

$$\begin{align*} i^{(t)} & = \sigma(W_i[x^{(t)}, h^{(t-1)}], b_i), & input gate \\ f^{(t)} & = \sigma(W_f[x^{(t)}, h^{(t-1)}], b_f), & forget gate \\ o^{(t)} & = \sigma(W_o[x^{(t)}, h^{(t-1)}], b_o), & output gate \\ \tilde C^{(t)} & = tanh((W_c[x^{(t)}, h^{(t)}])), & memory alternates \\ C^{(t)} & = f^{(t)} \odot c^{(t-1)} + i^{(t)} \odot c^{(t)}, & new memory \\ h^{(t)} & = o^{(t)} \odot tanh(c^{(t)}), & output \end{align*}$$

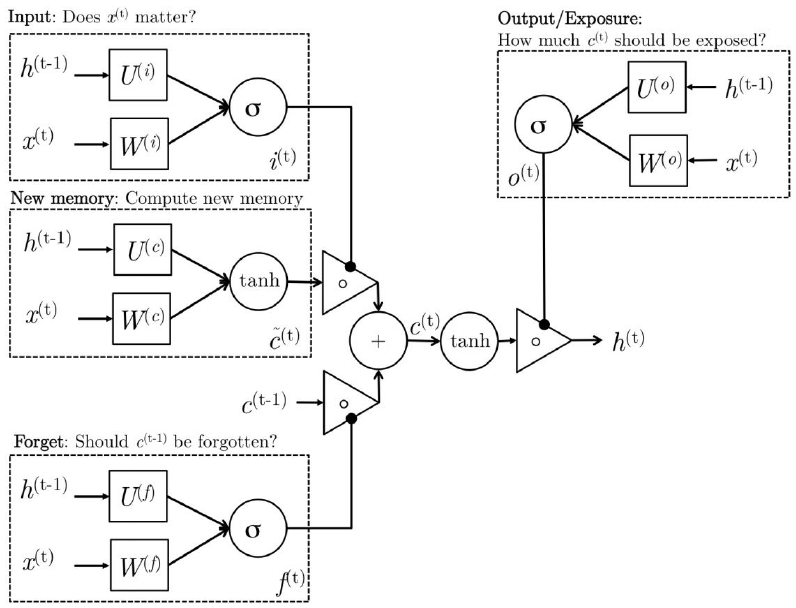
• $W_i, b_i, W_f, b_f, W_o, b_o$：输入门、遗忘门、输出门 参数
• $\odot$：逐项乘积
• $x_t$：第$t$期输入
• $i^{(t)}$：输出门权重，决定需要更新的信息
• $f^{(t)}$：遗忘门权重，决定需要遗忘的信息
• $o^{(t)}$：输出门权重，决定需要输出的信息
• $h^{(t-1)}$：第$t-1$期细胞状态输出
• $\tilde C_t$：第$t$期更新备选内容
• $C^{(t)}$：第$t$期更新完成后细胞状态

• 输入、遗忘、输出门特点

  • 当期输入$x^{(t)}$、上期输出$h^{(t-1)}$作为输入
  • sigmoid作为激活函数，得到$[0,1]$间控制、权重向量
    • 1：完全保留
    • 0：完全舍弃

• 细胞状态、输出特点

  • tanh作激活函数，得到$[-1,1]$间信息向量
    • $h^{(t-1)}, x^t$：备选更新信息输入
    • $C^{(t-1)}$：输出信息输入
  • 与门限权重逐项乘积确定最终遗忘、输入、输出

  • 细胞状态选择（候选、输出）都是使用双曲正切激活，应该 是为了有正由负

Gates

• Forget Gate：遗忘门，决定要从细胞状态中舍弃的信息

  

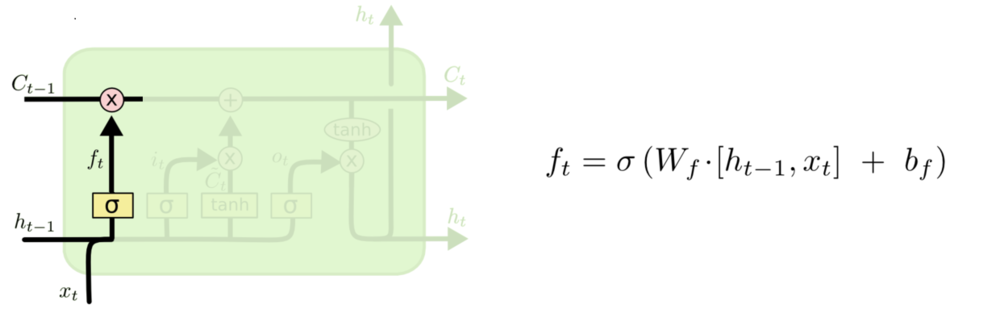
• Input Gate：输入门，决定向细胞状态中保留的信息

  

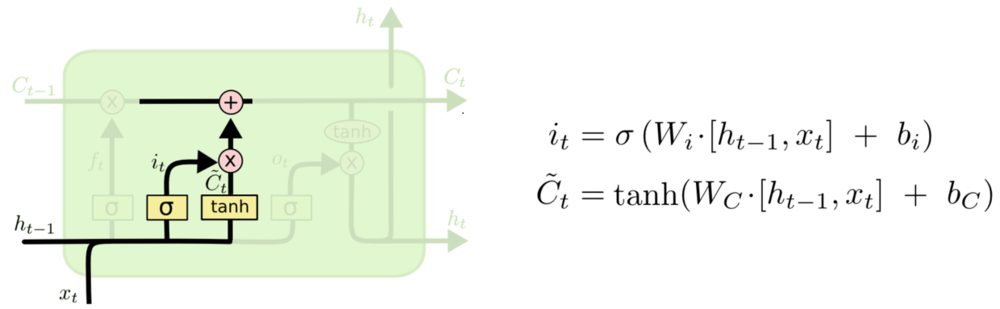
• Ouput Gate：输出门，决定从细胞状态中输出的信息

  

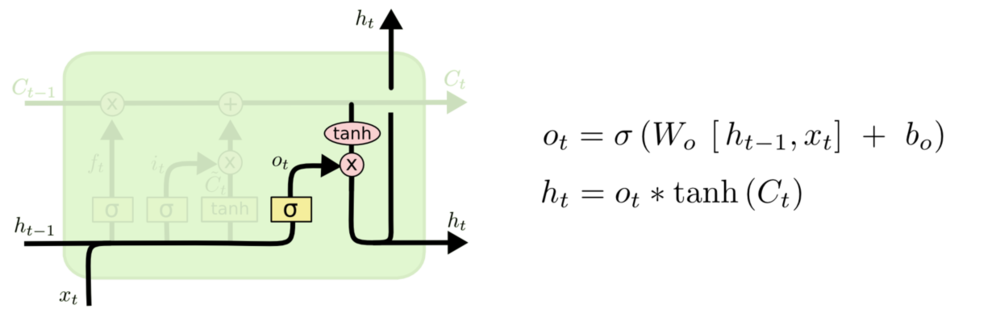
Cell State

细胞状态：LSTM中最重要的核心思想

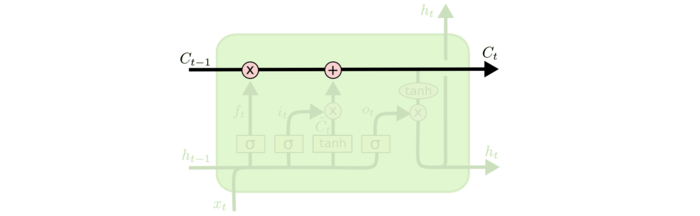
• 随着时间流动，承载之前所有状态信息，代表长期记忆

  • 类似于传送带，直接在整个链上运行，只有少量线性交互
  • 信息其上流派很容易保持不变
  • 通过“三个门”保护、控制

• LSTM可以保证长短时记忆可以理解为

  • $C_t$中历史信息比重由$f^{(t)}$确定
  • $f^{(t)}$趋近于1时历史信息能较好的保留

Gated Recurrent Unit

$$\begin{align*} r^{(t)} & = \sigma(W_r [h^{(t-1)}, x^{(t)}] + b_r), & reset gate \\ z^{(t)} & = \sigma(W_z [h^{(t-1)}, x^{(t)}] + b_z), & update gate \\ \tilde h^{(t)} &= tanh(W_h [r^{(t)} h^{(t-1)}, x^{(t)}]), & memory alternates\\ h^{(t)} & = (1 - z^{(t)}) \odot h^{(t-1)} + z^{(t)} \odot \tilde h^{(t)}, & new memory \end{align*}$$

• $W_r, b_r, W_z, b_z$：重置门、更新门参数
• $h^{(t)}$：原细胞状态、隐层输出合并
• $\tilde{h}_t$：第$t$期更新备选信息
• $r^{(t)}$：重置门权重输出，重置上期状态$h_{t-1}$再作为更新 门输入
• $z^{(t)]$：更新门权重输出，当期状态$ht$中$h{t-1}$、 $\tilde{h}_t$占比（遗忘、更新的结合）

• 合并细胞状态、隐层输出
• 合并遗忘门、输出门为更新门

其他变体结构

Vanilla LSTM

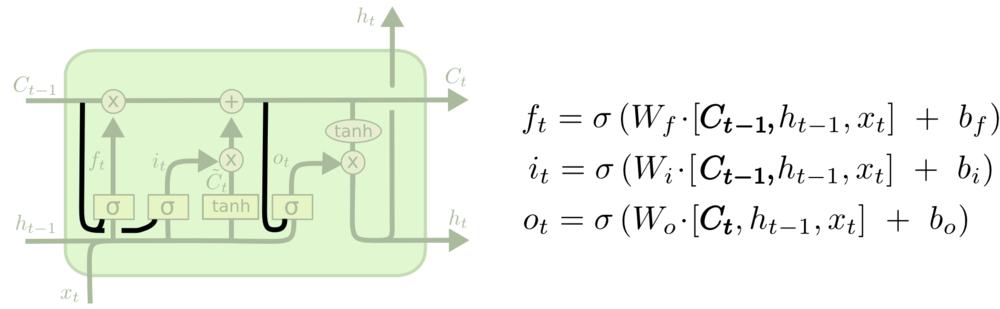
• Peephole Connection：细胞状态也作为3个门中sigmoid的 输入，影响控制向量的生成

Coupled Input and Forget Gate

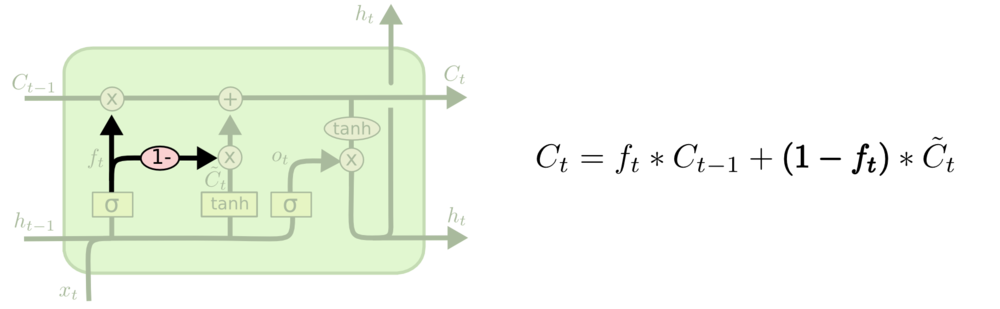
• $1-f_i$代替$i_t$，结合遗忘门、输入门

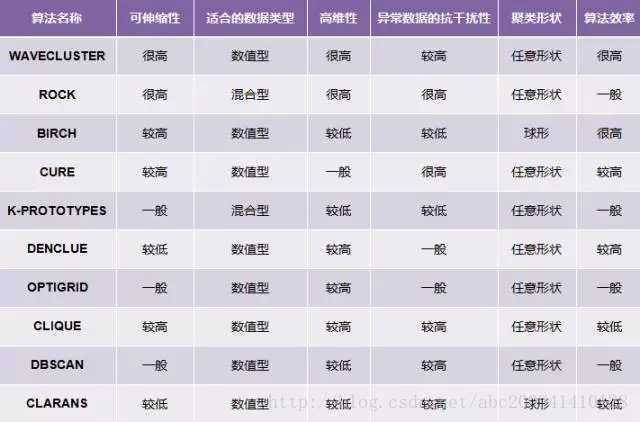
结构比较

在Vanilla LSTM基础上的8个变体在TIMIT语音识别、手写字符识别、 复调音乐建模三个应用中比较

• No Input Gate：NIG，没有输入门
• No Forget Gate：NFG，没有遗忘门
• No Output Gate：NOG，没有输出门
• No Input Acitivation Function：NIAF，输入门没有tanh 激活
• No Output Activation Function：NOAF，输出门没有tanh 激活
• No Peepholes：NP，普通LSTM
• Coupled Input and Forget Gate：CIFG，遗忘、输出门结合
• Full Gate Recurrence：FGR，所有门之间有回路

• Vanilla LSTM效果均良好，其他变体没有性能提升

• 细胞结构

  • 遗忘门、输入门是最重要的部分
    • 遗忘门对LSTM性能影响十分关键
    • 输出门对限制无约束细胞状态输出必要
  • CIFG、NP简化结构，单对结果没有太大影响

• 超参

  • 学习率、隐层数量是LSTM主要调节参数
    • 两者之间没有相互影响，可以独立调参
    • 学习率可以可以使用小网络结构独立校准
  • 动量因子影响不大
  • 高斯噪声的引入有损性能、增加训练时间

?时间

Seq2Seq

Seq2Seq/Encoder-Decoder：允许任意长度序列输入、输出学习

$$\begin{align*} p(y_1, \cdots, y_{T^{'}} | x_1, \cdots, x_T) & = \prod_{t=1}^T p(y_t|c, y_1, \cdots, y_{t-1}) \\ c & = q(\{h_1, \cdots, h_T\}) \\ h_t & = f(x_t, h_{t-1}) \end{align*}$$

• $T^{‘} \neq T$：输出序列长度、输入序列长度
• $p(y_t|\cdots)$：一般为softmax函数计算字典中各词概率
• $c$：定长向量
• $h_t$：隐状态
• $q$：将隐状态映射为定长向量存储信息，如： $q(\cdots) = h_T$
• $f$：根据输入映射为隐状态，如：RNN、LSTM

实现策略

• encoder：将输入序列映射为定长向量
• decoder：将该定长向量映射为目标输出 （通过将联合概率有序分解来定义翻译概率）

• RNN：以内部隐状态作为定长向量存储输入信息

  • 理论上可实现在定长向量中存储相关信息、再解码
  • 但由于长时梯度消失，实际难以训练

• LSTM：类似RNN在内部隐状态中存储信息

  • 学习长时依赖更有效、容易训练

Seq2Seq with Attention

• 采用LSTM、RNN结构的Seq2Seq结构很难将输入序列转化为定长 向量而保存所有有效信息

  • 序列末尾对定长向量影响更大，难以学习长距离依赖
  • 随着输入序列长度增加，预测效果显著下降

• 使用Attention机制的Seq2Seq无需多期迭代传递信息，不存在 长距离依赖

BiRNN2RNN with Attention

$$\begin{align*} p(y_t | y_1, \cdots, y_{t-1}, x) & = g(y_{t-1}, s_t, c_t) \\ s_t & = f(s_{t-1}, y_{t-1}, c_t) \\ c_t & = \sum_{j=t}^T \alpha_{j=1}^T \alpha_{t,j} h_j \\ \alpha_{t,j} & = softmax(e_{t,j}) \\ & = \frac {exp(e_{t,j})} {\sum_{k=1}^T exp(e_{t,k})} \\ e_{t,j} & = a(s_{t-1}, h_j) \end{align*}$$

• $y_t$：当前$t$时刻输出
• $p(y_t|\cdots)$：$t$时刻输出条件概率
• $s_t$：解码器$t$时刻隐状态
• $h_j$：编码器$j$时刻隐状态
• $c_t$：expected annotation，对输出$t$的上下文向量
• $T$：输入序列长度
• $e{t,j}, \alpha{t,j}$：输入$j$对输出$t$重要性，反映 模型注意力分布
• $a$：alignment model，输入输出相关性模型，同整个系统 联合训练的前向神经网络，attention机制核心

• 编码器：Bi-RNN
• 解码器：attention机制加权的RNN

因子分解机

因子分解机：将变量交互影响因子化 （每个变量用隐向量代表、衡量其交叉影响）

$$\hat y(x) := w_0 + \sum_{i=1}^m w_i x_i + \sum_{i=1}^m \sum_{j=i+1}^m <v_i, v_j> x_i x_j$$

• $w_0$：全局偏置
• $w_i$：变量$i$权重
• $w_{i,j} := $：变量$i$、$j$之间交互项权重
• $v_i$：$k$维向量，变量交叉影响因子

• FM通过因子化交互影响解耦交互项参数

  • 即使没有足够数据也能较好估计高维稀疏特征交互影响参数

    • 无需大量有交互影响（交互特征取值同时非0）样本
    • 包含某交互影响数据也能帮助估计相关的交互影响
    • 可以学习数据不存在的模式

  • 可以视为embedding，特征之间关联性用embedding向量 （隐向量）內积表示

• 参数数量、模型复杂度均为线性

  • 可以方便使用SGD等算法对各种损失函数进行优化
  • 无需像SVM需要支持向量，可以扩展到大量数据集

• 适合任何实值特征向量，对某些输入特征向量即类似 biased MF、SVD++、PITF、FPMC

• 另外还有d-way因子分解机，交互作用以PARAFAC模型因子化 $$\hat y(x) := w_0 + \sum_{i=1}^n w_i x_i + \sum_{l=2}^d \sum_{i_1=1} \cdots \sum_{i_l=i_{l-1}+1}(\prod_{j=1}^l x_{i_j}) (\sum_{f=1} \prod_{j=1}^l v_{i_j,f}^{(l)}) \\$$

  • $V^{(l)} \in R^{n * k_l}, k_l \in N_0^{+}$

模型表达能力

• 考虑任何正定矩阵$W$总可以被分解为$W=V V^T$，则$k$足够大 时，FM总可以表达（还原）交叉项权重矩阵$W$

  • FM是MF降维的推广，在用户-物品评分矩阵基础上集成其他 特征
  • 特征组合发生所有变量之间

• 实际应该选取较小的$k$

  • 对较大$k$，稀疏特征没有足够数据估计复杂交叉项权重 矩阵$W$
  • 限制FM的表达能力，模型有更好的泛化能力、交互权重矩阵

模型求解

$$\begin{align*} \sum_{i=1}^m \sum_{j=i+1}^m <v_i, v_j> x_i x_j & = \frac 1 2 \sum_{i=1}^m \sum_{j=i}^m <v_i, v_j> x_i x_j - \frac 1 2 \sum_{i=1}^m <v_i, v_i> x_i^2 \\ & = \frac 1 2 (x^T V^T V x - x^T diag(V^T V) x) \\ & = \frac 1 2 (\|Vx\|_2^2 - x^T diag(V^T V) x) \\ & = \frac 1 2 \sum_{f=1}^k ((\sum_{i=1}^m v_{i,f} x_i)^ 2 - \sum_{i=1}^m v_{i,f}^2 x_i^2) \\ \end{align*}$$

• $V = (v_1, v_2, \cdots, v_m)$
• $x = (x_1, x_2, \cdots, x_m)^T$

• 模型计算复杂度为线性$\in O(kn)$

• 模型可以使用梯度下降类方法高效学习

  $$\begin{align*} \frac {\partial \hat y(x)} {\partial \theta} & = \left \{ \begin{array}{l} 1, & \theta := w_0 \\ x_i, & \theta := w_i \\ x_i Vx - v_i x_i^2& \theta := v_i \end{array} \right. \\ & = \left \{ \begin{array}{l} 1, & \theta := w_0 \\ x_i, & \theta := w_i \\ x_i \sum_{j=1}^m v_{j,f} x_j - v_{i,f} x_i^2, & \theta := v_{i,f} \end{array} \right. \end{align*}$$

• 考虑到稀疏特征，內积只需计算非零值

模型适用

• 回归：直接用$\hat y(x)$作为回归预测值
• 二分类：结合logit损失、hinge损失优化
• ranking：$\hat y(x)$作为得分排序，使用成对分类损失优化

Field-aware Factorization Machines

域感知因子分解机：在FM基础上考虑对特征分类，特征对其他类别 特征训练分别训练隐向量

$$\begin{align*} \hat y(x) & = w_0 + \sum_{i=0}^m w_i x_i + \sum_{a=1}^m \sum_{b=a+1}^m <V_{a, f_b}, V_{b, f_a}> x_a x_b \\ & = w_0 + \sum_{i=1}^M \sum_{j=1}^{M_i} w_{i,j} x_{i,j} + \sum_{i=1}^M \sum_{j=1}^{M_i} \sum_{a=i}^M \sum_{b=1}^{M_i} <V_{i,j,a}, V_{a,b,i}> x_{i,j} x_{a,b} \end{align*}$$

• $m$：特征数量
• $M, M_i$：特征域数量、各特征域中特征数量
• $V_{i,j,a}$：特征域$i$中$j$特征对特征与$a$的隐向量
• $V_{a, f_b}$：特征$x_a$对特征$b$所属域$f_b$的隐向量

• FFM中特征都属于特定域，相同特征域中特征性质应该相同， 一般的

  • 连续特征自己单独成域
  • 离散0/1特征按照性质划分，归于不同特征域

• 特征对其他域分别有隐向量表示和其他域的隐含关系

  • 考虑交互作用时，对不同域使用不同隐向量计算交互作用
  • FFM中隐变量维度也远远小于FM中隐向量维度

算法

模型特点

• 模型总体类似FM，仅通过多样化隐向量实现细化因子分解
• 模型总体较FM复杂度大、参数数量多
  • 无法抽取公因子化简为线性
  • 数据量较小时可能无法有效训练隐向量

Internal Covariate Shift

ICS：由于网络参数变化，引起内部节点（输入）数据分布发生变化的过程

• 网络中层与层之间高度耦合，具有强关联性

  • 网络中任意层都可以视为单独网络
  • 上层输入可视为作为当前层外部输入

• 随训练进行，网络中参数不断发生改变

  • 任意层中参数变化会导致之后层输入发生改变
  • 高层需要不断适应输入分布的改变，即其输入分布性质影响 该层训练
  • 由此导致模型训练困难

负面影响

• 上层网络需要不断调整输入适应数据分布变换，降低网络学习 效率

• 输入数据量级不稳定、各维度数据量级差距不稳定

  • 降低学习效率
    • 小量级维度参数要求更小的学习率
    • 否则参数可能在最优解附近反复波动
  • 容易出现梯度消失，难以训练饱和非线性模型
    • 大量级维度训练过程中容易陷入梯度饱和区，参数更新 速度慢，减缓网络收敛速度
    • 训练过程中参数更新更有可能使得输入移向激活函数 饱和区
    • 且该效应随着网络深度加深被进一步放大
  • 参数初始化需要更复杂考虑

• 还可以使用非饱和激活函数ReLU等避免陷入梯度饱和区

Batch Normalization

Batch Normalization：规范化batch数据，使样本各维度 标准化，即均值为0、方差为1

$$\begin{align*} \y & = BN_{\gamma, \beta}(z) = \gamma \odot \hat z + \beta \\ \hat z & = \frac {z - E(z)} {\sqrt {Var(z) + \epsilon}} \end{align*}$$

• $B$：mini-batch
• $z, y$：某层输入向量、规范化后输入向量 （即以个神经元中激活前标量值$z=Wx+b$为一维）
• $\odot$：逐元素乘积
• $E(x)$：均值使用移动平均均值
• $Var(x)$：方差使用移动平均无偏估计
• $\gamma, \beta$：待学习向量，用于恢复网络的表示能力
• $\epsilon$：为数值计算稳定性添加

• BN可以视为whitening的简化

  • 简化计算过程：避免过高的运算代价、时间
  • 保留数据信息：未改变网络每层各特征之间相关性

• BN层引入可学习参数$\gamma, \beta$以恢复数据表达能力

  • Normalization操作缓解了ICS问题，使得每层输入稳定 ，也导致数据表达能力的缺失
  • 输入分布均值为0、方差为1时，经过sigmoid、tanh激活 函数时，容易陷入其线性区域
  • $\gamma = \sqrt {Var(z)}, \beta = E(z)$时为等价变换 ，并保留原始输入特征分布信息

• Whitening：白化，对输入数据变换使得各特征同均值、 同方向、不相关，可以分为PCA白化、ZCA白化

训练

• 规范化在每个神经元内部非线性激活前$z=Wu$进行，而不是 [也]在上一层输出$u$上进行，即包含BN最终为

  $$z = act(BN(Wu))$$

  • $act$：激活函数
  • 偏置$b$：可以被省略，BN中减去均值

  • $u$的分布形状可以在训练过程中改变
  • 而$u$两次正则化无必要
  • $z=Wu$分布更可能对称、稠密、类似高斯分布

• 以batch统计量作为整体训练样本均值、方差估计

  • 每层均需存储均值、方差的移动平均统计量用于测试时 归一化测试数据

• 对卷积操作，考虑卷积特性，不是只为激活函数（即卷积核） 学习$\gamma, \beta$，而是为每个feature map学习 （即每个卷积核、对每个特征图层分别学习）

预测

• 预测过程中各参数（包括均值、方差）为定值，BN仅仅对数据 做了线性变换

  • 使用训练总体的无偏统计量对测试数据归一化 （训练时存储）

    $$\begin{align*} \mu_{test} & = E(\mu_{batch}) \\ \sigma^2_{test} = \frac m {m-1} E(\sigma^2_{batch}) \end{align*}$$

  • 还可以使用样本指数加权平均统计量

用途

• BN通过规范化输入数据各维度分布减少ICS，使得网络中每层 输入数据分布相对稳定

• 实现网络层与层之间的解耦

  • 方便迁移学习
  • 加速模型学习速度：后层网络无需不断适应输入分布变化， 利于提高神经网络学习速度

• 降低模型对网络超参数、初始值敏感度，使得网络学习更加稳定

  • 简化调参过程
  • 允许使用更大的学习率提高学习效率
  $$\begin{align*} BN(Wu) & = BN((aW)u) \\ \frac {\partial BN(aWu)} {\partial u} & = \frac {\partial BN(Wu)} {\partial u} \\ \frac {BN(aWu)} {\partial aW} & = \frac 1 a \frac {\partial BN(Wu)} {\partial W} \end{align*}$$

  • $a$：假设某层权重参数变动$a$倍

  • 激活函数函数输入不受权重$W$放缩影响
  • 梯度反向传播更稳定，权重$W$的Jacobian矩阵将包含接近 1的奇异值，保持梯度稳定反向传播

• 允许网络使用饱和激活函数（sigmoid、tanh等），而不至于 停滞在饱和处，缓解梯度消失问题

  • 深度网络的复杂性容易使得网络变化积累到上层网络中， 导致模型容易进入激活函数梯度饱和区

• 有正则化作用，提高模型泛化性能，减少对Dropout的需求

  • 不同batch均值、方差有所不同，为网络学习过程增加随机 噪声
  • 与Dropout关闭神经元给网络带来噪声类似，一定程度上 有正则化效果

Layer Normalization

层归一化：假设非线性激活前的输入随机变量分布接近，可以直接 基于每层所有非线性激活前输入估计均值、方差

$$\begin{align*} \mu^l & = \frac 1 H \sum_{i=1}^H h_i^l \\ \sigma^l &= \sqrt {\frac 1 H \sum_{i=1}^H (h_i^l - \mu^l)^2} \\ h^l & = W^l x^{l-1} + b^l \\ LN(h^l) & = \frac {g^l} {\sigma^l} \odot (h^l - \mu^l) + b^l \\ x^l & = g(LN(h^l)) \end{align*}$$

• $h^l$：第$l$隐层激活前值
• $\mu^l, \sigma^l$：第$l$隐层对应LN均值、方差 （标量，是同层神经元激活前值统计量）

• 相对于BN，其适应范围更广

  • 循环神经网络中，BN无法处理长于训练序列的测试序列
  • BN无法应用到在线学习、超大分布式模型任务，此时训练 batch较小，计算的均值、方差无法有效代表训练总体

• LN假设非线性激活前输入随机变量分布接近，而CNN网络中图像 边缘对应kernel大量隐藏单元未被激活，假设不成立，所以 CNN网络中LN效果没有BN效果好

Dropout

Dropout：训练时根据随机隐藏部分神经元、对应连接边避免 过拟合

固定概率丢弃

Dropout最简单方法：设置固定概率p，对每个神经元以概率p判定 是否需要保留

$$\begin{align*} y & = f(W * d(x) + b) \\ d(x) & = \left \{ \begin{array}{l} m \odot x, & 训练阶段 px, & 测试阶段 \end{array} \right. \end{align*}$$

• $d(x)$：丢弃函数
• $m \in {0, 1}^d$：丢弃掩码，通过概率为p的伯努利 分布随机生成

• $p$可以设置为0.5，对大部分网络、任务比较有效

  • 此时随机生成多的网络最具多样性

• 训练时

  • 激活神经元数量为原来的p倍
  • 每个batch分别进行drop，相当于对每个batch都有独特网络

• 测试时

  • 所有神经元都被激活，造成训练、测试时网络输出不一致， 需将每个神经元输出乘p避免
  • 也相当于把不同网络做平均

• 在预测时，类似bagging技术将多个模型组合

  • 只是类似，各个drop后的子网并不独立，在不同子网中相同 神经元的权重相同
  • 多个模型组合组合可以一定程度上抵消过拟合
  • 因为在训练时子网中部分神经元被drop，剩余部分权重相较 完全网络有$\frac 1 {1-p}$，所以在完整网络中，各部分 权重需要$ * (1-p)$

• 讲道理应该是隐藏部分神经元而不是连接，否则会使神经元偏向 某些输入，还不如隐藏部分神经元，这样可以让神经元随机降低 样本权重，理论上能减弱过拟合

丢弃方法

• 输入层神经元丢弃率更接近1，使得输入变化不会太大

  • 输入层神经元丢失时，相当于给数据增加噪声，提高网络 稳健性

• 循环神经网络丢弃

  • 不能直接丢弃隐状态，会损害循环网络在时间维度上的记忆 能力
  • 简单方法：可以考虑对非循环连接进行随机丢弃
  • 变分丢弃法：根据贝叶斯对丢弃法是对参数的采样解释， 采样参数需要每个时刻保持不变
    • 需要对参数矩阵的每个元素随机丢弃
    • 所有时刻使用相同的丢弃掩码

解释

• 集成学习解释

  • 每次丢弃，相当于从原网络采样得到子网络
  • 每次迭代，相当于训练不同的子网络，共享原始网络参数
  • 最终网络可以近似看作是集成了指数个不同网络的组合模型

• 贝叶斯学习解释

  • 对需要学习的网络$y = f(x, \theta)$，贝叶斯学习假设 参数$\theta$为随机向量

  • 设先验分布为$q(\theta)$，贝叶斯方法预测为

    $$\begin{align*} E_{q(\theta)}[y] & = \int_q f(x, \theta) q(\theta) d\theta \\ & \approx \frac 1 M \sum_{m=1}^M f(x, \theta_m) \end{align*}$$

  • $f(x, \theta_m)$：第$m$次应用丢弃方法的网络
  • $\theta_m$：对全部参数的采样

Stacked Generalization

堆栈泛化：使用多种模型分别训练训练，将其结果叠加作为下层 模型的输入，最终得到预测输出

• 属于异源集成模型，可以视为

  • 复合函数

    

  • 短路网络

    

• 从某种意义上，复杂模型都是stacking

思想

• 不同模型侧重于获取数据不同方面的特征

  • 使用基学习器抽取数据特征进行表示学习，提取不同角度的 数据高维特征
  • 考虑到使用全量训练数据训练、预测作为下层模型输入会 导致过拟合，可使用K折交叉验证避免过拟合
  • 有些基学习器只使用适合其部分特征训练
    • GBDT、DNN适合低维稠密特征

• 元学习器组合多个基学习器的输出

  • 从数据高维特征学习数据模式，具有更好的泛化能力，避免 过拟合

算法

• 输入：模型$M1, M_2, \cdots, M_d$、训练特征：$X{n*m}$、 训练标签$Y_{n}$、测试特征$X^{‘}$
• 输出：stacking模型、预测标签

• 将训练数据K折划分，对第$i$轮划分

  • 使用模型$M1, M_2, \cdots, M_d$分别在相应训练集 $[X[:n_i,:], X[n{i+1}:,:]]$、 $[Y[:ni], Y[n{i+1}:]]$上训练
  • 在相应验证集$X[ni:n{i+1}, :]$上验证、并记录验证 结果
  • 将验证集验证结果叠加得到部分样本新特征 $N[ni: n{i+1}, d]$

• 将K轮划分得到的部分新特征拼接得到训练集的完整新特征 $N_{n * d}$，将新特征作为输入，训练下层模型，得到最终 stacking模型

• 将测试特征如上作为输入经过两层模型预测，得到最终预测结果

• 以上以2层stacking为例，有深层stacking

常用模型

基学习器

• 交叉项、原始特征本身也可以视为线性基学习器学习到的特征

• 具体模型参见 ml_specification/rec_system/ctr_stacking_models

GBDT

• 各树中各节点对应元学习器一维输入特征

• 适合低维稠密通用特征，对输入特征分布没有要求

• GBDT树根据熵增益（Gini系数增益）划分节点，每条路径 都代表一定区分能力

  • 以叶子节点（路径）作为特征，相当于自动进行特征 转换、组合、选择、离散化，得到高维组合特征

• GDBT相较于单棵树、或RF更适合stacking

  • 单棵树表达能力弱，无法表达多个有区分性特征组合， 集成模型可将样本映射为多个特征
  • GBDT拟合残差意味着各树对样本区分度不同，对各特征 区别对待更合理

DNN

• 适合普通稠密特征、embedding特征
• 模型表达能力强，能抽取有良好分布数据的深层次特征，提高 模型准确性、泛化能力
• 容易扩充其他类别特征，如：图片、文字

元学习器

• LR

  • 适合低维稀疏特征，可对所有特征离散化以引入非线性

• FM

  • 适合低维稀疏特征
  • LR基础上自动组合二阶交叉项

• Linear：训练模型、对训练结果线性加权

?

频繁项集

• 频繁项集：频繁出现项集合（无序）
• 频繁项序列：频繁出现项序列（有序）

• 相关关联规则算法：数据量大时，无法直接发现频繁项集
• 频繁项集评估标准

评估标准

• 支持度：数据关联出现概率，关联数据在数据集中出现次数占 总数据集比重

  $$Support(X, Y) = P(XY) = \frac {num(XY)} {num(All)}$$
  • 支持度高数据不一定构成频繁项集，但支持度数据肯定不能 不构成频繁项集

• 置信度：数据出现条件概率，某个数据出现、另一数据出现概率

  $$Confidence(X \Leftarrow Y) = P(X|Y) = \frac {P(XY)} {P(Y)}$$

• 提升度：数据之间关联关系，某数据出现、另一数据出现概率同 其总体出现概率之比

  $$\begin{align*} Lift(X \Leftarrow Y) & = \frac {P(X|Y)} {P(X)} \\ & = \frac {Confidence(X \Leftarrow)}{P(X)} \\ & = \frac {P(XY)} {P(X)P(Y)} \end{align*}$$
  • 提升度大于1则为有效的强关联规则，否则为无效的强关联 规则
  • 若X、Y不相关，则提升度为1

• 选择频繁数据集，一般需要自定义评估标准：自定义支持度、 自定义支持度和置信度组合

Apriori

Apriori算法

• 以支持度作为评估标准，找出数据集中最大的频繁$k$项集
  • 找到符合支持度标准的频繁$k$项集
  • 迭代直到无法找到项数更大的频繁项集

算法

• 输入：数据集合D、支持度阈值$\alpha$
• 输出：最大的频繁K项集

• 置$k=1$，扫描整个数据集，以所有出现过数据作为候选1项集
• 挖掘候选$k$项集
  • 扫描数据、计算候选$k$项集支持度
  • 去除支持度低于阈值$\alpha$的项集得到频繁$k$项集
    • 若频繁$k$项集只包含1项，直接返回
    • 若频繁$k$项集为空，返回频繁$k-1$项集
  • 基于频繁$k$项集连接、生成候选$k+1$项集
  • 置$k=k+1$

• 需要频繁扫描数据、效率低
• 频繁项集的子项集肯定也是频繁项集

FPTree/FPGrowth

FPTree：对Apriori算法改进，不在需要多次扫描数据

• FPTree引入部分数据结构以临时存储数据

  

  • 项头表：按频繁1项集出现频数降序排列的表
  • FP Tree：包含原始数据、频数的多叉树
  • 节点链表：链接项头表中频繁1项集、FPTree中相应节点 的链表

• 特点：效率高

  • 只需要扫描两次数据
  • 使用多叉树存储临时数据，利用高频频繁项集

算法

• 建立项头表

  • 扫描数据，得到所有1项集频数、剔除支持度低于阈值者， 并按支持度（频数）降序排列
  • 第二次扫描数据，剔除每条数据中非频繁1项集、 在每条数据内部按支持度降序排列

  

• 建立FPTree：逐条读取处理后排序后数据，依次插入树中

  • 每条数据中排序靠前者为祖先节点
  • 若有直系公共祖先则公共祖先节点计数+1
  • 新节点通过链表和项头表链接

  

• 挖掘FPTree：对项表头中每项，找到其条件模式基

  • 将子树中每个节点计数置为叶子节点计数和，则子树中节点 取值即为其与当前项组合出现频数/支持度
  • 删除（当前子树内）支持度/频数低于支持度阈值$\alpha$ 节点
  • 剩余节点项、当前项组合即为相应频繁$k$项集

  

  • 条件模式基：节点作为叶子节点所对应的FP子树

Prefix-Projected Pattern Growth

PrefixSpan：前缀投影模式挖掘

• 以支持度为标准，挖掘数据集中频繁序列
  • 每条数据为若干项集组成的序列，序列内项集间有序
  • 为方便，每条数据序列中项集中的项已排序

• 可以将每条数据序列整体视为串
• 频繁序列：频繁出现子序列

算法

• 输入：序列数据集$S$、支持度$\alpha$
• 所有满足阈值要求的频繁序列

• 找出所有长度1前缀（即所有项）、对应投影

  • 计数、剔除持度小于阈值$\alpha$者，得到频繁1项序列
  • 置$k=1$

• 对每个长度为$k$前缀递归挖掘

  • 若前缀对应投影为空，返回
  • 若前缀对应投影中所有项支持度均小于阈值$\alpha$，返回
  • 同满足阈值要求阈值$\alpha$要求项合并，得到新前缀
  • 置$k=k+1$

• prefix：前缀，正在处理的子序列
• projected：投影，各数据序列中位于前缀之后子串 ?串

聚类算法

聚类：按照某特定标准（如距离准则）把数据集分割成不同类、簇， 簇内数据相似性尽可能大、不同簇间数据对象差异性仅可能大

• 属于无监督学习，目标是把相似的样本聚集在一起

  • 通常只需要给定相似度的计算即可
  • 无需使用训练数据学习

• 聚类算法分类

  • 基于划分
  • Hierarchical Methods：基于层次
  • 基于密度
  • 基于网络
  • 基于模型
  • 模糊聚类
  • 基于约束
  • 基于粒度
  • 谱聚类
  • 核聚类
  • 量子聚类

衡量聚类算法优劣

• 算法的处理能力

  • 处理大数据的能力
  • 处理噪声数据能力
  • 处理任意形状数据的能力，如：有间隙的嵌套数据

• 算法是否需要预测条件

  • 聚类数目
  • 相关领域知识

• 输入数据关联性

  • 结果是否和数据输入顺序相关
  • 对数据维度敏感性（是否能处理高维数据）
  • 对数据类型要求

Hierarchical Methods

层次聚类

• 自底向上合并的层次聚类

  • 最底层开始，通过合并最相似类簇形成上层类簇
  • 全部数据点合并到同一类簇、或达到终止条件时结束

• 自顶向下分裂的层次聚类

  • 从包含全部数据点的类簇开始，递归分裂出最相异的下层 类簇
  • 每个类簇仅包含单个数据点时结束

• 优点

  • 可解释性好：如需要创建分类方法时
  • 研究表明能产生高质量聚类，可以应用在较大K的K-means 后的合并阶段
  • 可以解决非球形类簇

• 缺点

  • 时间复杂度高$O(N^2 log N)$（$N$为数据点数目）
  • 贪心算法无法取得最优解

• 距离选择参见ml_tech/#todo

AGENS

AGENS：自下向上层次聚类

• 组连接：组与组之间距离
  • single linkage
  • average linkage
  • complete linkage
• 算法复杂度：$n^2logn$

流程

• 每个数据点视为一类，计算两两直接最小距离
• 合并距离最小两个两类别为新类
• 重新计算新类、所有类之间距离
• 重复以上，直至所有类合并为一类

Divisive Analysis

DIANA：自定向下层次聚类

算法流程

• 所有数据归为一组$C_1=(p_1, p_2, dots, p_n)$
• 计算所有点之间的距离矩阵，选择到其他点平均距离最大的点， 记为$q$，取该点作为新组起始点
• $\forall p, p \notin C_1$，计算 $d_arg(p, C_1) - d_arg(p, C_2)$， 若小于零则属于$C_1$，否则属于$C_2$

Balanced Itertive Reducing and Clustering Using Hierarchies

BIRCH：利用层次方法的平衡迭代规约和聚类，利用层次方法聚类 、规约数据

• 特点
  • 利用CF树结构快速聚类
  • 只需要单遍扫描数据
  • 适合在数据类型为数值型、数据量大时使用

常见算法、改进

• A Hierarchical Clustering Algorithm Using Dynamic Modeling：使用KNN算法计算作为linkage、构建图
  • 较BIRCH好，但算法复杂度依然为$O(n^2)$
  • 可以处理比较复杂形状

Partition-Based Methods

基于划分的方法

• 基本流程

  • 确定需要聚类的数目，挑选相应数量点作为初始中心点
  • 再根据预定的启发式算法队数据点做迭代
  • 直到达到类簇内点足够近、类簇间点足够远

• 优点

  • 对大型数据集同样简单高效、时空复杂度低

• 缺点

  • 数据集越大，结果容易越容易陷入局部最优
  • 需要预先设置k值，对初始k中心点选取敏感
  • 对噪声、离群点敏感
  • 只适合数值性
  • 不适合非凸形状

• 影响结果因素

  • 原始问题是否可分
  • 分类数目K
  • 初始点选择

K-means

• 数据：$\Omega={X_1, X_2, \dots, X_N}$，分k个组

  $$C_1, C_2, \dots, C_k \\ C_1 \cup C_2 \cup \dots \cup C_k = \Omega \\$$

  每个样本点包含p个特征：$X_i = (x_1, x_2, \dots, x_p)$

• 目标：极小化每个样本点到聚类中心距离之和

  $$\arg_{C_1, C_2, \dots, C_K} \min \sum_{i=1}^K \sum_{x_j in \C_i} d(x_j, C_i)$$
  • 若定义距离为平方欧式距离，则根据组间+组内=全， 极小化目标就是中心点距离极大化

• 优化问题是NP-hard问题，需要采用近似方法

K值选择

• 经验选择
• 特殊方法：Elbow Method，肘部法则，画出距离和K的点图， 选择剧烈变化的点的K值

Lloyd’s Algorithm

• 随机选择K对象，每个对象初始地代表类簇中心
• 对剩余对象，计算与各簇中心距离，归于距离最近地类簇
• 重新计算各类簇平均值作为新簇中心
• 不断重复直至准则函数收敛

• 算法时间效率：$\in O(K * N^{\pi})$

常见算法、改进

• K-means++、Intelligent K-means、Genetic K-means：改进 K-means对初值敏感
• K-medoids、K-medians：改进K-means对噪声、离群点敏感
• K-modes：适用于分类型数据
• Kernel-Kmeans：可以解决非凸问题

Density-Based Methods

基于密度的方法

• 优点
  • 对噪声不敏感
  • 能发现任意形状聚类
• 缺点
  • 聚类结果和参数关系很大

相关概念

• 核心点：半径eps的邻域内点数量不少于阈值MinPts的点

• 直接可达：核心点半径eps的领域内被称为直接可达

  • 没有任何点是由非核心点直接可达的

• 可达：若存在$p_1, \cdots, p_n$点列中相邻点直接可达， 则$p_1, p_n$可达

  • 非对称关系，因为核心点没有直接可达点

• 连接性：若存在点$o$可达$p,q$，则$p,q$称为[密度]连接

  • 对称关系
  • 聚类内点都是相连接的
  • 若p由q可达，则p在q所属聚类中

• 局外点：不由任何点可达的点

DBSCAN

• Density-Based Spatial Clustering of Applications with Noise

算法流程

• 从任意对象点p开始
• 寻找合并核心点p对象直接密度可达对象
  • 若p是核心点，则找到聚类
  • 若p是边界，则寻找下个对象点
• 重复直到所有点被处理

说明

• DBSCAN用固定参数识别聚类，类簇稀疏程度不同时，相同判断 标准会破坏类自然结构

  • 较稀疏类簇会被划分为多个
  • 密度大距离近多个类被合并

• 参数影响

  • eps过大大多数点聚为同一簇中、过小则会导致簇分裂
  • MinPts值过大则同簇中点被标记为噪声点、过小则有大量 核心点

• 超参半径eps、最小点数量MinPts经验选取

  • 计算所有点k距离
  • 对各点k距离排序、绘制折线图
  • 观察折线图，以发现极具变化的位置对应k距离作为半径
  • k即作为最小点数量

  • k距离：距离点第k近点距离

常见算法、改进

• Ordering Points to Indentify Clustering Structure：优先 搜索高密度，然后根据高密度特点设置参数，改善DBSCAN

Grid-Based Methods

基于网络的方法

• 优点

  • 速度快，速度与数据对象个数无关，只依赖数据空间中每维 上单元数目
  • 可以和基于密度算法共同使用

• 缺点

  • 对参数敏感
  • 无法处理不规则分布的数据
  • 维数灾难
  • 聚类结果精确性低：算法效率提高的代价

流程

• 将数据空间划分为网格单元：不同算法主要区别
• 将数据对象集映射到网格单元中，计算各单元密度
• 根据预设的阈值判断每个网格单元是否为高密度单元
• 将相连的高度密度网格单元识别为类簇

常见算法、改进

• statistical information grid
• wave-cluster
• clustering-quest

Model-Based Methods

基于模型的方法：为每个类簇假定模型，寻找对给定模型的最佳拟合

• 优点
  • 对类划分以概率形式表示
  • 每类特征可以用概率表达
• 缺点
  • 执行效率不高，尤其是分布数量多、数据量少时

SOM

SOM：假设输入对象中存在一些拓扑结构、顺序，可以实现从输入 空间到输入平面的降维映射，且映射具有拓扑特征保持性质

• 网络结构

  • 输入层：高维输入向量
  • 输入层：2维网络上的有序节点

• 学习过程

  • 找到、更新与输入节点距离最短的输出层单元，即获胜单元
  • 更新邻近区域权值，保持输出节点具有输入向量拓扑特征

SOM算法流程

• 网络初始化：初始化输出层节点权重
• 随机选取输入样本作为输入向量，找到与输入向量距离最小的 权重向量
• 定义获胜单元，调整获胜单元邻近区域权重、向输入向量靠拢
• 收缩邻域半径、减小学习率、重复，直到小于允许值，输出聚类 结果

常见算法

• 概率生成模型：假设数据是根据潜在概率分布生成
  • Gaussian Mixture Model
• 基于神经网络模型的方法
  • Self Organized Maps

模糊聚类

模糊聚类：样本以一定概率属于某个类

• 优点
  • 对正态分布的数据聚类效果较好
  • 算法对孤立点敏感

Fuzzy C-means(FCM)

FCM：对K-means的推广软聚类

• 算法最终输出$C$个聚类中心向量、$C*N$模糊划分矩阵

  • 表示每个样本点对每个类的隶属度
  • 根据划分矩阵、按照最大隶属原则确定样本点归属
  • 聚类中心表示类平均特征，可以作为类代表

• 特点

  • 算法性能依赖初始聚类中心，需要依赖其他算法快速确定 初始聚类中心、或多次执行算法
  • 不能确保收敛于最优解

• soft cluster：点可以属于多个类

参数选择

• 聚类数目$C$：$C$远远小于聚类样本总数目，且大于1
• 柔性参数$m$
  • $m$过大：聚类效果差
  • $m$过小：算法接近HCM聚类算法

算法流程

• 标准化数据矩阵
• 建立模糊相似矩阵，初始化隶属矩阵

• 迭代，直到目标函数收敛到极小值

  $$w_k(x_i) = \frac 1 \sum_{i=1}^k (\frac {d(x_i, \mu_k)} {d(x_i, \mu_i} )^{1/(m-2)})$$

• 根据迭代结果，由最终隶属矩阵确定数据所属类，得到聚类结果

常见算法、改进

• HCM算法

基于约束的算法

基于约束的算法：考虑聚类问题中的约束条件，利用约束知识进行 推理

• 约束

  • 对聚类参数的约束
  • 对数据点的约束

• 典型算法

  • Clustering with Obstructed Distance：用两点之间障碍 距离取代一般的欧式距离计算最小距离

量子聚类

量子聚类：用量子理论解决聚类过程中初值依赖、确定类别数目的 问题

• 典型算法
  • 基于相关点的Pott自旋、统计机理提供的量子聚类模型： 将聚类问题视为物理系统

核聚类

核聚类：增加对样本特征的优化过程，利用Mercer核把输入空间映射 至高维特征空间，在特征空间中进行聚类

• 特点

  • 方法普适
  • 性能上优于经典聚类算算法
  • 可以通过非线性映射较好分辨、提取、放大有用特征
  • 收敛速度快

• 典型算法

  • SVDD算法
  • SVC算法

谱聚类

谱聚类：建立在图论中谱图理论基础上，本质是将聚类问题转换为 图的最优划分问题

基本流程

• 根据样本数据集定义描述成对数据点的相似度亲和矩阵
• 计算矩阵特征值、特征向量
• 选择合适的特征向量聚类不同点

Emsemble Learning

• 集成学习：训练多个基模型，并将其组合起来，以达到更好的 预测能力、泛化能力、稳健性
• base learner：基模型，基于独立样本建立的、一组 具有相同形式的模型中的一个
• 组合预测模型：由基模型组合，即集成学习最终习得模型

• 源于样本均值抽样分布思路

  • $var(\bar{X}) = \sigma^2 / n$
  • 基于独立样本，建立一组具有相同形式的基模型
  • 预测由这组模型共同参与
  • 组合预测模型稳健性更高，类似于样本均值抽样分布方差 更小

• 关键在于

  • 获得多个独立样本的方法
  • 组合多个模型的方法

分类

• homogenous ensemble：同源集成，基学习器属于同一类型

  • bagging
  • boosting

• heterogenous ensemble：异源集成，基学习器不一定属于同 一类型

  • [genralization] stacking

• 以上都是指原始版本、主要用途

Boosting

提升方法：将弱可学习算法提升为强可学习算法的组合元算法

• 属于加法模型：即基函数的线性组合
• 各模型之间存在依赖关系

分类Boosting

• 依次学习多个基分类器
• 每个基分类器依之前分类结果调整权重
• 堆叠多个分类器提高分类准确率

• boosting通过组合多个误分率略好于随机猜测的分类器得到 误分率较小的分类器，因此boosting适合这两类问题

  • 个体之间难度有很大不同，boosting能够更加关注较难的 个体
  • 学习器对训练集敏感，boosting驱使学习器在趋同的、 “较难”的分布上学习，此时boosting就和bagging一样能够 使得模型更加稳健（但原理不同）

• boosting能减小预测方差、偏差、过拟合

  • 直觉上，使用在不同的样本上训练的基学习器加权组合， 本身就能减小学习器的随机变动

  • 基于同样的理由，boosting同时也能减小偏差

  • 过拟合对集成学习有些时候有正面效果，其带来多样性， 使模型泛化能力更好，前提是样本两足够大，否则小样本 仍然无法提供多样性

回归Boosting

• 依次训练多个基学习器
• 每个基学习器以之前学习器拟合残差为目标
• 堆叠多个学习器减少整体损失

• boosting组合模型整体损失（结构化风险）

  $$R_{srm} = \sum_{i=1}^N l(y_i, \hat y_i) + \sum_{t=1}^M \Omega(f_t)$$

  • $l$：损失函数
  • $f_t$：基学习器
  • $\Omega(f_t)$：单个基学习器的复杂度罚
  • $N, M$：样本数目、学习器数目

• 基学习器损失

  $$obj^{(t)} = \sum_{i=1}^N l(y_i, \hat y_i^{(t)}) + \Omega(f_t)$$

最速下降法

使用线性函数拟合$l(y_i, \hat y_i^{(t)})$

$$\begin{align*} obj^{(t)} & = \sum_i^N l(y_i, \hat y_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) \\ & \approx \sum_{i=1}^N [l(y_i, \hat y^{(t-1)}) + g_i f_t(x_i)] + \Omega(f_t) \end{align*}$$

• $gi = \partial{\hat y} l(y_i, \hat y^{t-1})$

• 一次函数没有极值
• 将所有样本损失视为向量（学习器权重整体施加），则负梯度 方向损失下降最快，考虑使用负梯度作为伪残差

Newton法

使用二次函数拟合$l(y_i, \hat y_i^{(t)}$

$$\begin{align*} obj^{(t)} & = \sum_i^N l(y_i, \hat y_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) \\ & \approx \sum_{i=1}^N [l(y_i, \hat y^{(t-1)}) + g_i f_t(x_i) + \frac 1 2 h_i f_t^2(x_i)] + \Omega(f_t) \\ \end{align*}$$

• $hi = \partial^2{\hat y} l(y_i, \hat y^{t-1})$

• 二次函数本身有极值
• 可以结合复杂度罚综合考虑，使得每个基学习器损失达到最小

Boosting&Bagging

• 基分类器足够简单时，boosting表现均显著好于bagging

  • 仅靠单次决策（单个属性、属性组合）分类

• 使用C4.5树作为基分类器时，boosting仍然具有优势，但是不够 有说服力

• 结论来自于Experiments with a New Boosting Algorithm

Boosting&Bagging

• 基分类器足够简单时，boosting表现均显著好于bagging

  • 仅靠单次决策（单个属性、属性组合）分类

• 使用C4.5树作为基分类器时，boosting仍然具有优势，但是不够 有说服力

• 结论来自于Experiments with a New Boosting Algorithm

原理

probably approximately correct：概率近似正确，在概率近似 正确学习的框架中

• strongly learnable：强可学习，一个概念（类），如果存在 一个多项式的学习算法能够学习它，并且正确率很高，那么 就称为这个概念是强可学习的

• weakly learnable：弱可学习，一个概念（类），如果存在 一个多项式的学习算法能够学习它，学习的正确率仅比随机猜测 略好，称此概念为弱可学习的

• Schapire证明：在PAC框架下强可学习和弱可学习是等价的

具体措施

• 弱学习算法要比强学习算法更容易寻找，所以具体实施提升就是 需要解决的问题

• 改变训练数据权值、概率分布的方法

  • 提高分类错误样本权值、降低分类正确样本权值

• 将弱学习器组合成强学习器的方法

  • competeing
  • simple majority voting
  • weighted majority voting
  • confidence-based weighting

学习器组合方式

• 很多模型无法直接组合，只能组合预测结果

• simple majority voting/simple average：简单平均

  $$h = \frac 1 K \sum_{k=1}_K h_k$$

  • $h_k$：第k个预测

• weighted majority voting/weighted average：加权平均

  $$h = \frac {\sum_{k=1}^K w_k h_k} {\sum_{k=1}^K w_k}$$

  • $w_k$：第k个预测权重，对分类器可以是准确率

• competing voting/largest：使用效果最优者

• confidence based weighted：基于置信度加权

  $$\begin{align*} h = \arg\max_{y \in Y} \sum_{k=1}^K ln(\frac {1 - e_k} {e_k}) h_k \end{align*}$$

  • $e_k$：第k个模型损失

Meta Learning

元学习：自动学习关于关于机器学习的元数据的机器学习子领域

• 元学习主要目标：使用学习到元数据解释，自动学习如何 flexible的解决学习问题，借此提升现有学习算法性能、 学习新的学习算法，即学习学习

• 学习算法灵活性即可迁移性，非常重要

  • 学习算法往往基于某个具体、假象的数据集，有偏
  • 学习问题、学习算法有效性之间的关系没有完全明白，对 学习算法的应用有极大限制

要素

• 元学习系统必须包含子学习系统
• 学习经验通过提取元知识获得经验，元知识可以在先前单个 数据集，或不同的领域中获得
• 学习bias（影响用于模型选择的前提）必须动态选择
  • declarative bias：声明性偏见，确定假设空间的形式 ，影响搜索空间的大小
    • 如：只允许线性模型
  • procedural bias：过程性偏见，确定模型的优先级
    • 如：简单模型更好

Recurrent Neural networks

RNN：self-referential RNN理论上可以通过反向传播学习到， 和反向传播完全不同的权值调整算法

Meta Reinforcement Learning

MetaRL：RL智能体目标是最大化奖励，其通过不断提升自己的学习 算法来加速获取奖励，这也涉及到自我指涉

Additional Model

加法模型：将模型视为多个基模型加和而来

$$f(x) = \sum_{m=1}^M \beta_m b(x;\theta_m)$$

• $b(x;\theta_m)$：基函数
• $\theta_m$：基函数的参数
• $\beta_m$：基函数的系数

• 则相应风险极小化策略

  $$\arg\min_{\beta_m, \theta_m} \sum_{i=1}^N L(y_i, \sum_{m=1}^M \beta_m b(x_i;\theta_m))$$

  • $L(y, f(x))$：损失函数

Forward Stagewise Algorithm

前向分步算法：从前往后，每步只学习加法模型中一个基函数 及其系数，逐步逼近优化目标函数，简化优化复杂度

• 即每步只求解优化

  $$\arg\min_{\beta, \theta} \sum_{i=1}^N L(y_i, \hat f_m(x_i) + \beta b(x_i;\theta))$$

  • $\hat f_m$：前m轮基函数预测值加和

步骤

• 输入：训练数据集$T={(x_1,y_1), \cdots, (x_N,y_N)}$，损失 函数$L(y,f(x))$，基函数集${b(x;\theta)}$
• 输出：加法模型$f(x)$

• 初始化$f_0(x)=0$

• 对$m=1,2,\cdots,M$，加法模型中M个基函数

  • 极小化损失函数得到参数$\beta_m, \theta_m$

    $$(\beta_m, \theta_m) = \arg\min_{\beta, \theta} \sum_{i=1}^N L(y_i, f_{m-1}(x_1) + \beta b(x_i; \theta))$$

  • 更新

    $$f_m(x) = f_{m-1}(x) + \beta_m b(x;y_M)$$

• 得到加法模型

  $$f(x) = f_M(x) = \sum_{i=1}^M \beta_m b(x;\theta_m)$$

AdaBoost&前向分步算法

AdaBoost（基分类器loss使用分类误差率）是前向分步算法的特例， 是由基本分类器组成的加法模型，损失函数是指数函数

• 基函数为基本分类器时加法模型等价于AdaBoost的最终分类器 $f(x) = \sum_{m=1}^M \alpha_m G_m(x)$

• 前向分步算法的损失函数为指数函数$L(y,f(x))=exp(-yf(x))$ 时，学习的具体操作等价于AdaBoost算法具体操作

  • 假设经过m-1轮迭代，前向分步算法已经得到

    $$\begin{align*} f_{m-1}(x) & = f_{m-2}(x) + \alpha_{m-1}G_{m-1}(x) \\ & = \alpha_1G_1(x) + \cdots + \alpha_{m-1}G_{m-1}(x) \end{align*}$$

  • 经过第m迭代得到$\alpha_m, G_m(x), f_m(x)$，其中

    $$\begin{align*} (\alpha_m, G_m(x)) & = \arg\min_{\alpha, G} \sum_{i=1}^N exp(-y_i(f_{m-1}(x_i) + \alpha G(x_i))) \\ & = \arg\min_{\alpha, G} \sum_{i=1}^N \bar w_{m,i} exp(-y_i \alpha G(x_i)) \end{align*}$$

    • $\bar w{m,i}=exp(-y_i f{m-1}(x_i))$：不依赖 $\alpha, G$

  • $\forall \alpha > 0$，使得损失最小应该有 （提出$\alpha$）

    $$\begin{align*} G_m^{*}(x) & = \arg\min_G \sum_{i=1}^N \bar w_{m,i} exp(-y_i f_{m-1}(x_i)) \\ & = \arg\min_G \sum_{i=1}^N \bar w_{m,i} I(y_i \neq G(x_i)) \end{align*}$$

    此分类器$G_m^{*}$即为使得第m轮加权训练误差最小分类器 ，即AdaBoost算法的基本分类器

  • 又根据

    $$\begin{align*} \sum_{i=1}^N \bar w_{m,i} exp(-y_i \alpha G(x_i)) & = \sum_{y_i = G_m(x_i)} \bar w_{m,i} e^{-\alpha} + \sum_{y_i \neq G_m(x_i)} \bar w_{m,i} e^\alpha \\ & = (e^\alpha - e^{-\alpha}) \sum_{i=1}^N (\bar w_{m,i} I(y_i \neq G(x_i))) + e^{-\alpha} \sum_{i=1}^N \bar w_{m,i} \end{align*}$$

    带入$G_m^{*}$，对$\alpha$求导置0，求得极小值为

    $$\begin{align*} \alpha_m^{*} & = \frac 1 2 log \frac {1-e_m} {e_m} \\ e_m & = \frac {\sum_{i=1}^N (\bar w_{m,i} I(y_i \neq G_m(x_i)))} {\sum_{i=1}^N \bar w_{m,i}} \\ & = \frac {\sum_{i=1}^N (\bar w_{m,i} I(y_i \neq G_m(x_i)))} {Z_m} \\ & = \sum_{i=1}^N w_{m,i} I(y_i \neq G_m(x_i)) \end{align*}$$

    • $w_{m,i}, Z_M$同AdaBoost中

    即为AdaBoost中$\alpha_m$

  • 对权值更新有

    $$\bar w_{m+1,i} = \bar w_{m,i} exp(-y_i \alpha_m G_m(x))$$

    与AdaBoost权值更新只相差规范化因子$Z_M$

AdaBoost

通过改变训练样本权重，学习多个分类器，并将分类器进行线性 组合，提高分类性能

• 对离群点、奇异点敏感
• 对过拟合不敏感

Boosting实现

• 改变训练数据权值或概率分布：提高分类错误样本权值、降低 分类正确样本权值

• 弱分类器组合：加权多数表决，即加大分类误差率小的弱分类器 权值，使其在表决中起更大作用；减小分类误差率大的弱分类器 权值，使其在表决中起更小作用

步骤

• 输入：训练数据集$T={(x_1, y_1), \cdots, (x_N, y_N)}$， 弱分类器算法$G(x)$

  • $x_i \in \mathcal{X \subset R^n}$
  • $y_i \in \mathcal{Y} = {-1, +1 }$

• 输出：最终分类器$G(x)$

• 初始化训练数据权值分布： $D1=(w{11}, \cdots, w{1N}), w{1i}=\frac 1 N$

• 对$m=1,2,\cdots,M$（即训练M个弱分类器）

  • 使用具有权值分布$D_m$的训练数据学习，得到基本 分类器

    $$G_m(x):\mathcal{X} \rightarrow \{-1, +1\}$$

  • 计算$G_m(x)$在训练数据集上的分类误差率

    $$\begin{align*} e_m & = P(G_m(x_i)) \neq y_i) \\ & = \sum_{i=1}^N w_{mi}I(G_m(x_i) \neq y_i) \\ & = \sum_{G_m(x_i) \neq y_i} w_{mi} \end{align*}$$

  • 计算$G_m(x)$组合为最终分类器时权重

    $$\alpha = \frac 1 2 log \frac {1-e_m} {e_m}$$

    • $\alpha_m$表示就简单分类器$G_m(x)$在最终分类器中 的重要性，随$e_m$减小而增加 （弱分类器保证$e_m \leq 1/2$）

  • 更新训练集权值分布

    $$\begin{align*} D_{m+1} & = (w_{m+1,1}, \cdots, w_{m+1,N}) \\ w_{m+1,i} & = \frac {w_{mi}} {Z_m} exp(-\alpha y_i G_m(x_i)) = \left \{ \begin{array}{l} \frac {w_mi} {Z_m} e^{-\alpha_m}, & G_m(x_i) = y_i \\ \frac {w_mi} {Z_m} e^{\alpha_m}, & G_m(x_i) \neq y_i \\ \end{array} \right. \\ Z_m & = \sum_{i=1}^N w_{mi} exp(-\alpha_m y_i G_m(x_i)) \end{align*}$$

    • $Zm$：规范化因子，是第m轮调整后的权值之和，其 使得$D{m+1}$成为概率分布
    • 误分类样本权值相当于被放大 $e^{2\alpha_m} = \frac {e_m} {1 - e_m}$倍

• 构建基本分类器线性组合

  $$f(x) = \sum_{m=1}^M \alpha_m G_m(x)$$

  得到最终分类器

  $$G(x) = sign(f(x)) = sign(\sum_{m=1}^M \alpha_m G_m(x))$$

  • 这里$\alpha_m$没有规范化，和不为1，规范化没有必要
  • $f(x)$符号决定分类预测结果，绝对值大小表示分类确信度

• AdaBoost中分类器学习和之后的分类误差率“无关”，基分类器 学习算法中的loss不是分类误差率，可以是其他loss，只是需要 考虑训练数据的权值分布

  • 好像基学习器的loss就要是和集成部分调权的loss一致

    todo

  • 按权值分布有放回的抽样，在抽样集上进行训练
  • 各样本loss按权重加权，类似分类误差率中加权

训练误差边界

AdaBoost算法最终分类器的训练误差边界为

$$\frac 1 N \sum_{i=1}^N I(G(x_i) \neq y_i) \leq \frac 1 N \sum_i exp(-y_if(x_i)) = \prod_m Z_m$$

• $G(x_i) \neq y_i$时，$y_if(x_i)<0$，所以 $exp(-y_i f(x_i)) \geq 1$，则不等式部分可证

• $$\begin{align*} \frac 1 N \sum_i exp(-y_i f(x_i)) & = \frac 1 N \sum_i exp(-\sum_{m=1}^M \alpha_m y_i G_m(x_i)) \\ & = \sum_i (w_{1,i} \prod_{m=1}^M exp(-\alpha_m y_i G_m(x_i))) \\ & = \sum_i (Z_1 w_{2,i} \prod_{m=2}^M exp(-\alpha_m y_i G_m(x_i))) \\ & = \prod_{m=1}^M Z_i \sum_i w_{M+1,i} \\ & = \prod_{m=1}^M Z_i \end{align*}$$

• AdaBoost训练误差边界性质的关键：权重调整与基本分类器权重 调整共系数（形式不完全一样）
• 这也是AdaBoost权重调整设计的依据，方便给出误差上界

二分类训练误差边界

$$\prod_{m=1}^M Z_m = \prod_{m=1}^M (2\sqrt{e_m(1-e_m)}) = \prod_{m=1}^M \sqrt{(1-4\gamma_m^2)} \leq exp(-2\sum_{m=1}^M \gamma_m^2)$$

• $\gamma_m = \frac 1 2 - e_m$

• $$\begin{align*} Z_m & = \sum_{i=1}^N w_{m,i} exp(-\alpha y_i G_m(x_i)) \\ & = \sum_{y_i = G_m(x_i)} w_{m,i}e^{-\alpha_m} + \sum_{y_i \neq G_m(x_i)} w_{m,i}e^{\alpha_m} \\ & = (1-e_m)e^{-\alpha_m} + e_m e^{\alpha_m} \\ & = 2\sqrt{e_m(1-e_m)} \\ & = \sqrt{1-4\gamma^2} \end{align*}$$

• 由$\forall x \in [0, 0.5], e^{-x} > \sqrt{1-2x}$可得， $\sqrt{1-4\gamma_m^2} \leq exp(-2\gamma_m^2)$

• 二分类AdaBoost误差边界性质的关键：$\alpha$的取值，也是 前向分步算法（损失函数）要求
• 若存$\gamma > 0$，对所有m有$\gamma_m \geq \gamma$，则 $$\frac 1 N \sum_{i=1}^N I(G(x_i) \neq y_i) \neq exp(-2M\gamma^2)$$ 即AdaBoost的训练误差是指数下降的
• 分类器下界$\gamma$可以未知，AdaBoost能适应弱分类器各自 训练误差率，所以称为adptive

Adaboost.M1

Adaboost.M1是原版AdaBoost的多分类升级版，基本思想同Adaboost

Boosting实现

• 基分类器组合方式

  • 仍然是加权投票，且投票权重同Adaboost
  • 出于多分类考虑，没有使用sign符号函数

• 改变训练数据权值或概率分布：和Adaboost形式稍有不同，但 相对的错误分类样本提升比率完全相同

  • 被上个分类器错误分类样本，权值保持不变
  • 被上个分类器正确分类样本，权值缩小比例是Adaboost平方

步骤

• 输入

  • 训练集：$T={x_i, y_i}, i=1,\cdots,N; y_i \in C, C={c_1, \cdots, c_m}$
  • 训练轮数：T
  • 弱学习器：I

• 输出：提升分类器

  $$H(x) = \arg\max_{y \in C} \sum_{m=1}^M ln(\frac 1 {\beta_m}) [h_m(x) = y]$$

  • $h_t, h_t(x) \in C$：分类器
  • $\beta_t$：分类器权重

误分率上界

• 对弱学习算法产生的伪损失$\epsilon1,\cdots,\epsilon_t$， 记$\gamma_t = 1/2 \epsilon_t$，最终分类器$h{fin}$误分率 上界有 $$\frac 1 N |\{i: h_{fin}(x_i) \neq y_i \}| \leq \prod_{t-1}^T \sqrt {1-4\gamma^2} \leq exp(-2 \sum_{t-1}^T \gamma^2)$$

特点

Adaboost.M1和Adaboost基本上没有区别

• 类别数目为2的Adaboost.M1就是Adaboost
• 同样无法处理对误分率高于0.5的情况，甚至在多分类场合， 误分率小于0.5更加难以满足
• 理论误分率上界和Adaboost相同

Adaboost.M2

AdaboostM2是AdaboostM1的进阶版，更多的利用了基分类器信息

• 要求基学习器能够输出更多信息：输出对样本分别属于各类别 的置信度向量，而不仅仅是最终标签
• 要求基分类器更加精细衡量错误：使用伪损失代替误分率 作为损失函数

Psuedo-Loss

$$\begin{align*} L & = \frac 1 2 \sum_{(i,y) \in B} D_{i,y} (1 - h(x_i, y_i) + h(x_i, y)) \\ & = \frac 1 2 \sum_{i=1}^N D_i (1 - h(x_i, y_i) + \sum_{y \neq y_i} (w_{i,y} h(x_i, y))) \end{align*}$$

• $D$：权重分布（行和为1，但不满足列和为1）

  • $D_{i,y}$：个体$x_i$中错误标签$y$的权重，代表从个体 $x_i$中识别出错误标签$y$的重要性

• $B = {(i, y)|y \neq y_i, i=1,2,\cdots,N }$
• $w$：个体各错误标签权重边际分布
• $h(x, y)$：模型$h$预测样本$x$为$y$的置信度

  • $h(x_i,y_i)$：预测正确的置信度
  • $h(x_i,y), y \neq y_i$：预测$x_i$为错误分类$y$置信度

• 伪损失函数同时考虑了样本和标签的权重分布
• 通过改变此分布，能够更明确的关注难以预测的个体标签， 而不仅仅个体

Boosting实现

• 改变数据权值或者概率分布

  • 使用psuedo-loss替代误分率，以此为导向改变权值
  • 对多分类每个错误分类概率分别计算错误占比，在此基础上 分别计算

• 基分类器组合方式：同Adaboost.M1

步骤

训练误差上界

• 对弱学习算法产生的伪损失$\epsilon1,\cdots,\epsilon_t$， 记$\gamma_t = 1/2 \epsilon_t$，最终分类器$h{fin}$误分率 上界有

$$\frac 1 N |\{i: h_{fn}(x_i) \neq y_i \}| \leq (M-1) \prod_{t-1}^T \sqrt {1-4\gamma^2} \leq (M-1) exp(-2 \sum_{t-1}^T \gamma^2)$$

特点

• 基于伪损失的Adaboost.M2能够提升稍微好于随机预测的分类器

• Adaboosting.M2能够较好的解决基分类器对噪声的敏感性，但是 仍然距离理论最优Bayes Error有较大差距，额外误差主要 来自于

  • 训练数据
  • 过拟合
  • 泛化能力

• 控制权值可以有效的提升算法，减小最小训练误差、过拟合 、泛化能力

  • 如对权值使用原始样本比例作为先验加权

• 其分类结果不差于AdaBoost.M1（在某些基分类器、数据集下）