二叉树衍生

Huffman Tree

哈夫曼树/最优树：带权路径长度WPL最短的树

• 哈夫曼树中没有度为1的结点，又称为严格的（正则的）二叉树

• 树带权路径长度：树中所有叶子结点的带权路径长度之和 $WPL = \sum_{k=1}^n w_k l_k$

哈夫曼算法

哈夫曼算法：构建最小加权路径二叉树

• 输入：给定的n个权值${w_1, w_2, \cdots, w_n}$

• 初始化n个单节点二叉树集合$F={T_1, T_2, \cdots, T_n}$
• 合并权重最小的两棵树，将其权重之和作为新树权重记录于新树 根节点中
• 重复，直至生成单独一棵树

特点

• 贪婪算法
• Huffman算法构建的最优二叉树是只有叶子节点有权值，若所有 节点都有权值的最优二叉查找树，需要使用动态规划算法， 参见cs_algorithm/data_structure/tree_search

哈夫曼编码

• 哈夫曼编码：编码总长度最短的二进制前缀编码
• 前缀编码：任意编码都不是其他编码的前缀，此时编码可以

• 前缀编码可以使用二叉树设计，叶子结点代表字符，根节点到 叶子结点路径上分支代表的二进制串即为其二进制编码

• 对给定出现频率$P[1..n]$的字符集$C[1..n]$，生成哈夫曼树 即可得到哈夫曼编码

链式存储

哈夫曼树

typedef struct HTNode{
	unsigned int weight;
	struct HTNode *parent, *lchild, *rchild;
}HTNode, *HuffmanTree;

选拔树

优胜树

优胜树：非叶结点取值是两个孩子中较小者的完全二叉树

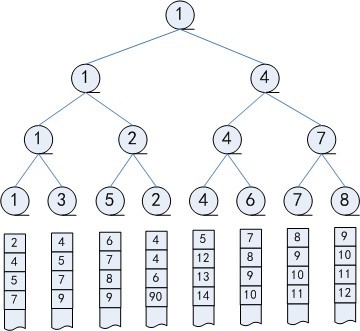
• 根据定义，根节点的取值是整个树的最小值
• 从叶节点构建/重构优胜树的过程中
  • 每对兄弟结点捉对比赛，胜利者晋升为父亲结点
  • 胜者逐级向上直到根节点为止
  • 调整优胜树的时间效率$\in \Theta(logk)$

顺序存储结构

typedef SqBiTree SqVictTree;

• 数组实现的二叉树可以通过完全二叉树性质迅速计算父节点、 孩子节点位置

淘汰树

淘汰树：非叶结点值是两个孩子结点中较大者，即指向失败者的 选拔树

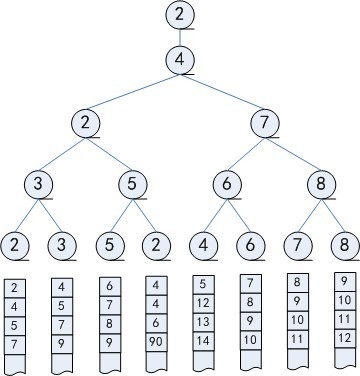
• 可以简化选拔树重构过程
• 需要额外结点记录/指向胜者

用途

归并多路有序序列

• 问题：k路有序（降序）序列，要将其归并为一组有序序列， 归并过程每轮输出一个最小关键字记录 （显然只能是当前k路序列中第一个记录）

• 以k路序列首k个元素建立k个叶节点的选拔树

• 构建选拔树，输出最小元素值

  

• 用其所属序列下个元素替换其所在叶节点值，重构选拔

  

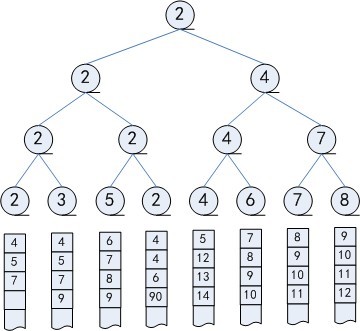
• 重复n轮：所有k轮归并总时间为$\in \Theta(nlogk)$

)$