Boosting

Gredient Boosting

GB：（利用）梯度提升，将提升问题视为优化问题，前向分步算法 利用最速下降思想实现

• 一阶展开拟合损失函数，沿负梯度方向迭代更新

  • 损失函数中，模型的样本预测值$f(x)$是因变量
  • 即$f(x)$应该沿着损失函数负梯度方向变化
  • 即下个基学习器应该以负梯度方向作为优化目标，即负梯度 作为伪残差

  • 类似复合函数求导

• 对基学习器预测值求解最优加权系数

  • 最速下降法中求解更新步长体现
  • 前向分布算法中求解基学习器权重

损失函数

基学习器拟合目标：损失函数的负梯度在当前模型的值

$$-\left [ \frac {\partial L(y, \hat y_i)} {\partial y_i} \right ]_{\hat y_i=\hat y_i^{(t-1)}}$$

平方损失

平方损失：$L(y, f(x)) = \frac 1 2 (y - f(x))^2$（回归）

• 第m-1个基学习器伪残差为

  $$r_{m,i} = y_i - f_{m-1}(x_i), i=1,2,\cdots,N$$

  • $N$：样本数量

• 第m个基学习器为

  $$\begin{align*} h_m & = \arg\min_h \sum_{i=1}^N \frac 1 2 (y_i - (f_{m-1}(x_i) + h(x)))^2 \\ & = \arg\min_h \sum_{i=1}^N \frac 1 2 (C_{m,i} - h(x))^2 \\ C_{m,i} & = y_i - f_{m-1}(x_i) \end{align*}$$

• 第m轮学习器组合为

  $$f_m = f_{m-1} + \alpha_m h_m$$

  • $\alpha_m$：学习率，留给之后基模型学习空间

  • 这里只是形式上表示模型叠加，实际上树模型等不可加， 应该是模型预测结果叠加

指数损失

指数损失：$L(y, f(x)) = e^{-y f(x)}$（分类）

• 第m-1个基学习器伪残差

  $$r_{m,i} = -y_i e^{-y_i f_{m-1}(x_i)}, i=1,2,\cdots,N$$

• 基学习器、权重为

  $$\begin{align*} h_m & = \arg\min_h \sum_{i=1}^N exp(-y_i(f_{m-1}(x_i) + \alpha f(x_i))) \\ & = \arg\min_h \sum_{i=1}^N C_{m,i} exp(-y_i \alpha f(x_i)) \\ C_{m,i} & = exp(-y_i f_{m-1}(x_i)) \end{align*}$$

• 第m轮学习器组合为

  $$f_m = f_{m-1} + \alpha_m h_m$$

步骤

• 输入：训练数据集$T={(x_1, y_1), \cdots, (x_N, y_N)}$， 损失函数$L(y, f(x))$

  • $x_i \in \mathcal{X \subset R^n}$
  • $y_i \in \mathcal{Y} = {-1, +1 }$

• 输出：回归树$\hat f(x)$

• 初始化模型

  $$\hat y_i^{(0)} = \arg\min_{\hat y} \sum_{i=1}^N L(y_i, \hat y)$$

• 对$m=1,2,\cdots,M$（即训练M个若分类器）

  • 计算伪残差

    $$r_i^{(t)} = -\left [ \frac {\partial L(y, \hat y_i)} {\partial y_i} \right ]_{\hat y_i=\hat y_i^{(t-1)}}$$

  • 基于${(x_i, r_i^{(t)})}$生成基学习器$h_t(x)$

  • 计算最优系数

    $$\gamma = \arg\min_\gamma \sum_{i=1}^N L(y_i, \hat y_i^{(t-1)} + \gamma h_t(x_i))$$

  • 更新预测值

    $$\hat y_i^{(t)} = \hat y_i^{(t-1)} + \gamma_t h_t (x)$$

• 得到最终模型

  $$\hat f(x) = f_M(x) = \sum_{t=1}^M \gamma_t h_t(x)$$

Gradient Boosted Desicion Tree

GBDT：梯度提升树，以回归树为基学习器的梯度提升方法

• GBDT会累加所有树的结果，本质上是回归模型（毕竟梯度）

  • 所以一般使用CART回归树做基学习器
  • 当然可以实现分类效果

• 损失函数为平方损失（毕竟回归），则相应伪损失/残差

  $$r_{t,i} = y_i - f_{t-1}(x_i), i=1,2,\cdots,N$$

特点

• 准确率、效率相较于RF有一定提升
• 能够灵活的处理多类型数据
• Boosting类算法固有的基学习器之间存在依赖，难以并行训练 数据，比较可行的并行方案是在每轮选取最优特征切分时，并行 处理特征

XGBoost

Extreme Gradient Boost/Newton Boosting：前向分步算法利用 Newton法思想实现

• 二阶展开拟合损失函数

  • 损失函数中，模型的样本预测值$\hat y_i$是因变量
  • 将损失函数对$\hat y_i$二阶展开拟合
  • 求解使得损失函数最小参数

• 对基学习器预测值求解最优加权系数

  • 阻尼Newton法求解更新步长体现
  • 前向分布算法中求解基学习器权重
  • 削弱单个基学习器影响，让后续基学习器有更大学习空间

损失函数

• 第t个基分类器损失函数

  $$\begin{align*} obj^{(t)} & = \sum_{i=1}^N l(y_i, \hat y_i^{(t)}) + \Omega(f_t) \\ & = \sum_i^N l(y_i, \hat y_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) \\ & \approx \sum_{i=1}^N [l(y_i, \hat y^{(t-1)}) + g_i f_t(x_i) + \frac 1 2 h_i f_t^2(x_i)] + \Omega(f_t) \\ & = \sum_{i=1}^N [l(y_i, \hat y^{(t-1)}) + g_i f_t(x_i) + \frac 1 2 h_i f_t^2(x_i)] + \gamma T_t + \frac 1 2 \lambda \sum_{j=1}^T {w_j^{(t)}}^2 \\ \Omega(f_t) & = \gamma T_t + \frac 1 2 \lambda \sum_{j=1}^T {w_j^{(t)}}^2 \end{align*}$$

  • $f_t$：第t个基学习器
  • $f_t(x_i)$：第t个基学习器对样本$x_i$的取值
  • $gi = \partial{\hat y} l(y_i, \hat y^{t-1})$
  • $hi = \partial^2{\hat y} l(y_i, \hat y^{t-1})$
  • $\Omega(f_t)$：单个基学习器的复杂度罚
  • $T_t$：第t个基学习器参数数量，即$L_0$罚

    • 线性回归基学习器：回归系数数量
    • 回归树基学习器：叶子节点数目

  • $\gamma$：基学习器$L_0$罚系数，模型复杂度惩罚系数
  • $w_j = f_t$：第t个基学习器参数值，即$L_2$罚

    • 线性回归基学习器：回归系数值
    • 回归树基学习器：叶子节点

  • $\lambda$：基学习器$L_2$罚系数，模型贡献惩罚系数
  • $\approx$：由二阶泰勒展开近似

• 对损失函数进行二阶泰勒展开（类似牛顿法）拟合原损失函数， 同时利用一阶、二阶导数求解下个迭代点

• 正则项以控制模型复杂度

  • 降低模型估计误差，避免过拟合
  • $L_2$正则项也控制基学习器的学习量，给后续学习器留下 学习空间

树基学习器

XGBoost Tree：以回归树为基学习器的XGBoost模型

• 模型结构说明

  • 基学习器类型：CART
  • 叶子节点取值作惩罚：各叶子节点取值差别不应过大，否则 说明模型不稳定，稍微改变输入值即导致输出剧烈变化
  • 树复杂度惩罚：叶子结点数量

• XGBoost最终损失（结构风险）有

  $$\begin{align*} R_{srm} & = \sum_{i=1}^N l(y_i, \hat y_i) + \sum_{t=1}^M \Omega(f_t) \end{align*}$$

  • $N, M$：样本量、基学习器数量
  • $\hat y_i$：样本$i$最终预测结果

损失函数

• 以树作基学习器时，第$t$基学习器损失函数为

  $$\begin{align*} obj^{(t)} & = \sum_{i=1}^N l(y_i, \hat y_i^{(t)}) + \Omega(f_t) \\ & \approx \sum_{i=1}^N [l(y_i, \hat y^{(t-1)}) + g_i f_t(x_i) + \frac 1 2 h_i f_t^2(x_i)] + \gamma T_t + \frac 1 2 \lambda \sum_{j=1}^T {w_j^{(t)}}^2 \\ & = \sum_{j=1}^{T_t} [(\sum_{i \in I_j} g_i) w_j^{(t)} + \frac 1 2 (\sum_{i \in I_j} h_i + \lambda) {w_j^{(t)}}^2] + \gamma T_t + \sum_{i=1}^N l(y_i, \hat y^{(t)}) \\ & = \sum_{j=1}^{T_t} [G_i w_j^{(t)} + \frac 1 2 (H_j + \lambda){w_j^{(t)}}^2] + \gamma T_t + \sum_{i=1}^N l(y_i, \hat y^{(t)}) \\ & = \sum_{j=1}^{T_t} [G_i w_j^{(t)} + \frac 1 2 (H_j + \lambda)(w_j^{(t)})^2] + \gamma T_t + \sum_{i=1}^N l(y_i, \hat y^{(t)}) \\ \end{align*}$$

  • $f_t, T_t$：第t棵回归树、树叶子节点
  • $f_t(x_i)$：第t棵回归树对样本$x_i$的预测得分
  • $w_j^{(t)} = f_t(x)$：第t棵树中第j叶子节点预测得分
  • $gi = \partial{\hat y} l(y_i, \hat y^{t-1})$
  • $hi = \partial^2{\hat y} l(y_i, \hat y^{t-1})$
  • $I_j$：第j个叶结点集合
  • $Gj = \sum{i \in I_j} g_i$
  • $Hj = \sum{i \in I_j} h_i$

  • 对回归树，正则项中含有$(w_j^{(t)})^2$作为惩罚，能够 和损失函数二阶导合并，不影响计算

  • 模型复杂度惩罚项惩罚项是针对树的，定义在叶子节点上， 而平方损失是定义在样本上，合并时将其改写

• 第t棵树的整体损失等于其各叶子结点损失加和，且 各叶子结点取值之间独立

  • 则第t棵树各叶子结点使得损失最小的最优取值如下 （$G_j, H_j$是之前所有树的预测得分和的梯度取值，在 当前整棵树的构建中是定值，所以节点包含样本确定后， 最优取值即可确定）

    $$w_j^{(*)} = -\frac {\sum_{i \in I_j} g_i} {\sum_{i \in I_j} h_i + \lambda} = -\frac {G_j} {H_j + \lambda}$$

  • 整棵树结构分数（最小损失）带入即可得

    $$obj^{(t)} = -\frac 1 2 \sum_{j=i}^M \frac {G_j^2} {H_j + \lambda} + \gamma T$$

  • 则在结点分裂为新节点时，树损失变化量为

    $$l_{split} = \frac 1 2 \left [ \frac {(\sum_{i \in I_L} g_i)^2} {\sum_{i \in I_L h_i} + \lambda} + \frac {(\sum_{i \in I_R} g_i)^2} {\sum_{i \in I_R h_i} + \lambda} - \frac {(\sum_{i \in I} g_i)^2} {\sum_{i \in I h_i} + \lambda} \right ] - \gamma$$

    • $I_L, I_R$：结点分裂出的左、右结点

• 则最后应根据树损失变化量确定分裂节点、完成树的分裂，精确 贪心分裂算法如下

  !xgb_exact_greedy_algorithm_for_split_finding

  • 对于连续型特征需遍历所有可能切分点

    • 对特征排序
    • 遍历数据，计算上式给出的梯度统计量、损失变化

  • 不适合数据量非常大、或分布式场景

模型细节

• shrinkage：对新学习的树使用系数$\eta$收缩权重

  • 类似SGD中学习率，降低单棵树的影响，给后续基模型留下 学习空间

• column subsampling：列抽样

  • 效果较传统的行抽样防止过拟合效果更好 （XGB也支持行抽样）
  • 加速计算速度

XGB树分裂算法

• 线性回归作为基学习器时，XGB相当于L0、L2正则化的 Logistic回归、线性回归

近似分割算法

XGB近似分割算法：根据特征分布选取分位数作为候选集，将连续 特征映射至候选点划分桶中，统计其中梯度值、计算最优分割点

!xgb_approximate_algorithm_for_split_finding

• 全局算法：在树构建初始阶段即计算出所有候选分割点，之后 所有构建过程均使用同样候选分割点

  • 每棵树只需计算一次分割点的，步骤少
  • 需要计算更多候选节点才能保证精度

• 局部算法：每次分裂都需要重新计算候选分割点

  • 计算步骤多
  • 总的需要计算的候选节点更少
  • 适合构建较深的树

• 分位点采样算法参见 ml_model/model_enhancement/gradient_boost

Sparsity-aware Split Finding

稀疏特点分裂算法：为每个树节点指定默认分裂方向，缺失值对应 样本归为该方向

• 仅处理非缺失值，算法复杂度和随无缺失数据集大小线性增加， 减少计算量

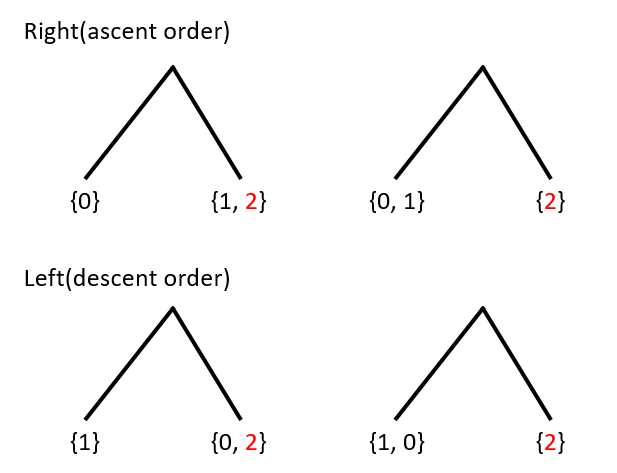
• 按照升许、降序分别扫描样本两轮，以便将缺失值样本分别归为 两子节点，确定最优默认分裂方向

  

XGB系统设计

Column Block for Parallel Learning

• 建树过程中最耗时的部分为寻找最优切分点，而其中最耗时部分 为数据排序

XGB对每列使用block结构存储数据

• 每列block内数据为CSC压缩格式

  • 特征排序一次，之后所有树构建可以复用（忽略缺失值）
  • 存储样本索引，以便计算样本梯度
  • 方便并行访问、处理所有列，寻找分裂点

• 精确贪心算法：将所有数据（某特征）放在同一block中

  • 可同时对所有叶子分裂点进行计算
  • 一次扫描即可得到所有叶子节点的分割特征点候选者统计 数据

• 近似算法：可以使用多个block、分布式存储数据子集

  • 对local策略提升更大，因为local策略需要多次生成分位点 候选集

Cache-aware Access

• 列block结构通过索引获取数据、计算梯度，会导致非连续内存 访问，降低CPU cache命中率

• 精确贪心算法：使用cache-aware prefetching

  • 对每个线程分配连续缓冲区，读取梯度信息存储其中，再 统计梯度信息
  • 对样本数量较大时更有效

• 近似算法：合理设置block大小为block中最多的样本数

  • 过大容易导致命中率低、过小导致并行化效率不高

Blocks for Out-of-core Computation

• 数据量过大不能全部存放在主存时，将数据划分为多个block 存放在磁盘上，使用独立线程将block读入主存 （这个是指数据划分为块存储、读取，不是列block）

• 磁盘IO提升

  • block compression：将block按列压缩，读取后使用额外 线程解压
  • block sharding：将数据分配至不同磁盘，分别使用线程 读取至内存缓冲区

分位点采样算法—XGB

Quantile Sketch

样本点权重

• 根据已经建立的$t-1$棵树可以得到数据集在已有模型上误差， 采样时根据误差对样本分配权重，对误差大样本采样粒度更大

• 将树按样本点计算损失改写如下

  $$\sum_{i=1}^N \frac 1 2 h_i(f_t(x_i) - \frac {g_i} {h_i})^2 + \Omega(f_t) + constant$$

• 则对各样本，其损失为$f_t(x_i) - \frac {g_i} {h_i}$ 平方和$h_i$乘积，考虑到$f_t(x_i)$为样本点在当前树预测 得分，则可以

  • 将样本点损失视为“二次损失”
  • 将$\frac {g_i} {h_i}$视为样本点“当前标签”
  • 相应将$h_i$视为样本点权重

• 样本权重取值示例

  • 二次损失：$h_i$总为2，相当于不带权
  • 交叉熵损失：$h_i=\hat y(1-\hat y)$为二次函数， 则$\hat y$接近0.5时权重取值大，此时该样本预测值 也确实不准确，符合预期

Rank函数

• 记集合$D={(x_1, h_1), \cdots, (x_n, h_n)}$

• 定义rank函数$r_D: R \rightarrow [0, +\infty)$如下

  $$r_D(z) = \frac 1 {\sum_{(x, h) \in D} h} \sum_{(x, h) \in D, x < z} h$$
  • 即集合$D$中权重分布中给定取值分位数
  • 即取值小于给定值样本加权占比，可视为加权秩

分位点抽样序列

• 分位点抽样即为从集合$D$特征值中抽样，找到升序点序列 $S = {s_1, \cdots, s_l}$满足

  $$|r_D(s_j - r_D(s_{j+1})| < \epsilon$$

  • $\epsilon$：采样率，序列长度$l = 1/\epsilon$
  • $s1 = \min{i} x_i$：特征最小值

  • $sl = \max{i} x_i$：特征最大值

  • 各样本等权分位点抽样已有成熟方法，加权分位点抽样方法 为XGB创新，如下

Weighted Quantile Sketch

Formalization

• 记$Dk={(x{1,k}, h1), \cdots, (x{n,k}, h_n)}$为各 训练样本第$k$维特征、对应二阶导数

  • 考虑到数据点可能具有相同$x, h$取值，$D_k$为可能包含 重复值的multi-set

• 对于多重集$D$，额外定义两个rank函数

  $$\begin{align*} r_D^{-}(y) & = \sum_{(x,h) \in D, x<y} h \\ r_D^{+}(y) & = \sum_{(x,h) \in D, x \leq y} h \end{align*}$$

  定义相应权重函数为

  $$w_D(y) = r_D^{+}(y) - r_D^{-}(y) = \sum_{(x,h) \in D, x=y} h$$

• 多重集$D$上全部权重和定义为

  $$w(D) = \sum_{(x, w) \in D} w$$

Quantile Summary of Weighted Data

• 定义加权数据上的quantile summary为 $Q(D)=(S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$

  • $S$为$D$中特征取值抽样升序序列，其最小、最大值分别 为$D$中特征最小、最大值

  • $\tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D$为定义在 $S$上的函数，满足

    $$\begin{align*} \tilde r_D^{-}(x_i) & \leq r_D^{-}(x_i) \\ \tilde r_D^{+}(x_i) & \leq r_D^{+}(x_i) \\ \tilde w_D(x_i) & \leq w_D(x_i) \\ \tilde r_D^{-}(x_i) + \tilde w_D(x_i) & \leq \tilde r_D^{-}(x_{i+1}) \\ \tilde r_D^{+}(x_i) + \tilde w_D(x_i) & \leq \tilde r_D^{+}(x_{i+1}) \\ \end{align*}$$

• $Q(D)$满足如下条件时，称为 $\epsilon$-approximate quantile summary

  $$\forall y \in D_X, \tilde r_D^{+}(y) - \tilde r_D(y) - \tilde w_D(y) \leq \epsilon w(D)$$
  • 即对任意$y$的秩估计误差在$\epslion$之内

• $\phi-quantile$：秩位于$\phi * N$的元素（一般向下取整）
• $\epsilon-\phi-quantile$：秩位于区间 $[(\phi-\epsilon)N, (\phi+\epsilon)N]$的元素

构建$\epsilon$-Approximate Qunatile Summary

• 初始化：在小规模数据集 $D={(x_1,h_1), \cdots, (x_n,h_n)}$上构建初始 初始quantile summary $Q(D)=(S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$ 满足

  $$\begin{align*} \tilde r_D^{-}(x_i) & \leq r_D^{-}(x_i) \\ \tilde r_D^{+}(x_i) & \leq r_D^{+}(x_i) \\ \tilde w_D(x_i) & \leq w_D(x_i) \end{align*}$$
  • 即初始化$Q(D)$为0-approximate summary

• merge operation：记 $Q(D1)=(S_1, \tilde r{D1}^{+}, \tilde r{D1}^{-}, \tilde w{D1})$、 $Q(D_2)=(S_2, \tilde r{D2}^{+}, \tilde r{D2}^{-}, \tilde w{D_2})$、 $D = D_1 \cup D_2$，则归并后的 $Q(D)=(S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$ 定义为

  $$\begin{align*} S & S_1 \cup S_2 \\ \tilde r_D^{-}(x_i) & = \tilde r_{D_1}^{-}(x_i) + \tilde r_{D_2}^{-}(x_i) \\ \tilde r_D^{+}(x_i) & = \tilde r_{D_1}^{+}(x_i) + \tilde r_{D_2}^{+}(x_i) \\ \tilde w_D(x_i) & = \tilde w_{D_1}(x_i) + \tilde w_{D_2}(x_i) \end{align*}$$

• prune operation：从给定 $Q(D)=(S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$， （其中$S = {x_1, \cdots, x_k }$），构建新的summary $\acute Q(D)=(\acute S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$

  • 仅定义域从$S$按如下操作抽取 $\acute S={\acute x1, \cdots, \acute x{b+1}}$

    $$\acute x_i = g(Q, \frac {i-1} b w(D))$$

  • $g(Q, d)$为查询函数，对给定quantile summary $Q$、 秩$d$返回秩最接近$d$的元素