聚类

聚类算法

聚类：按照某特定标准（如距离准则）把数据集分割成不同类、簇， 簇内数据相似性尽可能大、不同簇间数据对象差异性仅可能大

• 属于无监督学习，目标是把相似的样本聚集在一起

  • 通常只需要给定相似度的计算即可
  • 无需使用训练数据学习

• 聚类算法分类

  • 基于划分
  • Hierarchical Methods：基于层次
  • 基于密度
  • 基于网络
  • 基于模型
  • 模糊聚类
  • 基于约束
  • 基于粒度
  • 谱聚类
  • 核聚类
  • 量子聚类

衡量聚类算法优劣

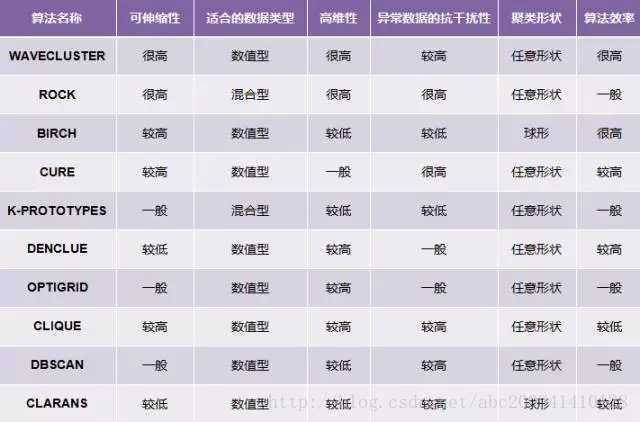
• 算法的处理能力

  • 处理大数据的能力
  • 处理噪声数据能力
  • 处理任意形状数据的能力，如：有间隙的嵌套数据

• 算法是否需要预测条件

  • 聚类数目
  • 相关领域知识

• 输入数据关联性

  • 结果是否和数据输入顺序相关
  • 对数据维度敏感性（是否能处理高维数据）
  • 对数据类型要求

Hierarchical Methods

层次聚类

• 自底向上合并的层次聚类

  • 最底层开始，通过合并最相似类簇形成上层类簇
  • 全部数据点合并到同一类簇、或达到终止条件时结束

• 自顶向下分裂的层次聚类

  • 从包含全部数据点的类簇开始，递归分裂出最相异的下层 类簇
  • 每个类簇仅包含单个数据点时结束

• 优点

  • 可解释性好：如需要创建分类方法时
  • 研究表明能产生高质量聚类，可以应用在较大K的K-means 后的合并阶段
  • 可以解决非球形类簇

• 缺点

  • 时间复杂度高$O(N^2 log N)$（$N$为数据点数目）
  • 贪心算法无法取得最优解

• 距离选择参见ml_tech/#todo

AGENS

AGENS：自下向上层次聚类

• 组连接：组与组之间距离
  • single linkage
  • average linkage
  • complete linkage
• 算法复杂度：$n^2logn$

流程

• 每个数据点视为一类，计算两两直接最小距离
• 合并距离最小两个两类别为新类
• 重新计算新类、所有类之间距离
• 重复以上，直至所有类合并为一类

Divisive Analysis

DIANA：自定向下层次聚类

算法流程

• 所有数据归为一组$C_1=(p_1, p_2, dots, p_n)$
• 计算所有点之间的距离矩阵，选择到其他点平均距离最大的点， 记为$q$，取该点作为新组起始点
• $\forall p, p \notin C_1$，计算 $d_arg(p, C_1) - d_arg(p, C_2)$， 若小于零则属于$C_1$，否则属于$C_2$

Balanced Itertive Reducing and Clustering Using Hierarchies

BIRCH：利用层次方法的平衡迭代规约和聚类，利用层次方法聚类 、规约数据

• 特点
  • 利用CF树结构快速聚类
  • 只需要单遍扫描数据
  • 适合在数据类型为数值型、数据量大时使用

常见算法、改进

• A Hierarchical Clustering Algorithm Using Dynamic Modeling：使用KNN算法计算作为linkage、构建图
  • 较BIRCH好，但算法复杂度依然为$O(n^2)$
  • 可以处理比较复杂形状

Partition-Based Methods

基于划分的方法

• 基本流程

  • 确定需要聚类的数目，挑选相应数量点作为初始中心点
  • 再根据预定的启发式算法队数据点做迭代
  • 直到达到类簇内点足够近、类簇间点足够远

• 优点

  • 对大型数据集同样简单高效、时空复杂度低

• 缺点

  • 数据集越大，结果容易越容易陷入局部最优
  • 需要预先设置k值，对初始k中心点选取敏感
  • 对噪声、离群点敏感
  • 只适合数值性
  • 不适合非凸形状

• 影响结果因素

  • 原始问题是否可分
  • 分类数目K
  • 初始点选择

K-means

• 数据：$\Omega={X_1, X_2, \dots, X_N}$，分k个组

  $$C_1, C_2, \dots, C_k \\ C_1 \cup C_2 \cup \dots \cup C_k = \Omega \\$$

  每个样本点包含p个特征：$X_i = (x_1, x_2, \dots, x_p)$

• 目标：极小化每个样本点到聚类中心距离之和

  $$\arg_{C_1, C_2, \dots, C_K} \min \sum_{i=1}^K \sum_{x_j in \C_i} d(x_j, C_i)$$
  • 若定义距离为平方欧式距离，则根据组间+组内=全， 极小化目标就是中心点距离极大化

• 优化问题是NP-hard问题，需要采用近似方法

K值选择

• 经验选择
• 特殊方法：Elbow Method，肘部法则，画出距离和K的点图， 选择剧烈变化的点的K值

Lloyd’s Algorithm

• 随机选择K对象，每个对象初始地代表类簇中心
• 对剩余对象，计算与各簇中心距离，归于距离最近地类簇
• 重新计算各类簇平均值作为新簇中心
• 不断重复直至准则函数收敛

• 算法时间效率：$\in O(K * N^{\pi})$

常见算法、改进

• K-means++、Intelligent K-means、Genetic K-means：改进 K-means对初值敏感
• K-medoids、K-medians：改进K-means对噪声、离群点敏感
• K-modes：适用于分类型数据
• Kernel-Kmeans：可以解决非凸问题

Density-Based Methods

基于密度的方法

• 优点
  • 对噪声不敏感
  • 能发现任意形状聚类
• 缺点
  • 聚类结果和参数关系很大

相关概念

• 核心点：半径eps的邻域内点数量不少于阈值MinPts的点

• 直接可达：核心点半径eps的领域内被称为直接可达

  • 没有任何点是由非核心点直接可达的

• 可达：若存在$p_1, \cdots, p_n$点列中相邻点直接可达， 则$p_1, p_n$可达

  • 非对称关系，因为核心点没有直接可达点

• 连接性：若存在点$o$可达$p,q$，则$p,q$称为[密度]连接

  • 对称关系
  • 聚类内点都是相连接的
  • 若p由q可达，则p在q所属聚类中

• 局外点：不由任何点可达的点

DBSCAN

• Density-Based Spatial Clustering of Applications with Noise

算法流程

• 从任意对象点p开始
• 寻找合并核心点p对象直接密度可达对象
  • 若p是核心点，则找到聚类
  • 若p是边界，则寻找下个对象点
• 重复直到所有点被处理

说明

• DBSCAN用固定参数识别聚类，类簇稀疏程度不同时，相同判断 标准会破坏类自然结构

  • 较稀疏类簇会被划分为多个
  • 密度大距离近多个类被合并

• 参数影响

  • eps过大大多数点聚为同一簇中、过小则会导致簇分裂
  • MinPts值过大则同簇中点被标记为噪声点、过小则有大量 核心点

• 超参半径eps、最小点数量MinPts经验选取

  • 计算所有点k距离
  • 对各点k距离排序、绘制折线图
  • 观察折线图，以发现极具变化的位置对应k距离作为半径
  • k即作为最小点数量

  • k距离：距离点第k近点距离

常见算法、改进

• Ordering Points to Indentify Clustering Structure：优先 搜索高密度，然后根据高密度特点设置参数，改善DBSCAN

Grid-Based Methods

基于网络的方法

• 优点

  • 速度快，速度与数据对象个数无关，只依赖数据空间中每维 上单元数目
  • 可以和基于密度算法共同使用

• 缺点

  • 对参数敏感
  • 无法处理不规则分布的数据
  • 维数灾难
  • 聚类结果精确性低：算法效率提高的代价

流程

• 将数据空间划分为网格单元：不同算法主要区别
• 将数据对象集映射到网格单元中，计算各单元密度
• 根据预设的阈值判断每个网格单元是否为高密度单元
• 将相连的高度密度网格单元识别为类簇

常见算法、改进

• statistical information grid
• wave-cluster
• clustering-quest

Model-Based Methods

基于模型的方法：为每个类簇假定模型，寻找对给定模型的最佳拟合

• 优点
  • 对类划分以概率形式表示
  • 每类特征可以用概率表达
• 缺点
  • 执行效率不高，尤其是分布数量多、数据量少时

SOM

SOM：假设输入对象中存在一些拓扑结构、顺序，可以实现从输入 空间到输入平面的降维映射，且映射具有拓扑特征保持性质

• 网络结构

  • 输入层：高维输入向量
  • 输入层：2维网络上的有序节点

• 学习过程

  • 找到、更新与输入节点距离最短的输出层单元，即获胜单元
  • 更新邻近区域权值，保持输出节点具有输入向量拓扑特征

SOM算法流程

• 网络初始化：初始化输出层节点权重
• 随机选取输入样本作为输入向量，找到与输入向量距离最小的 权重向量
• 定义获胜单元，调整获胜单元邻近区域权重、向输入向量靠拢
• 收缩邻域半径、减小学习率、重复，直到小于允许值，输出聚类 结果

常见算法

• 概率生成模型：假设数据是根据潜在概率分布生成
  • Gaussian Mixture Model
• 基于神经网络模型的方法
  • Self Organized Maps

模糊聚类

模糊聚类：样本以一定概率属于某个类

• 优点
  • 对正态分布的数据聚类效果较好
  • 算法对孤立点敏感

Fuzzy C-means(FCM)

FCM：对K-means的推广软聚类

• 算法最终输出$C$个聚类中心向量、$C*N$模糊划分矩阵

  • 表示每个样本点对每个类的隶属度
  • 根据划分矩阵、按照最大隶属原则确定样本点归属
  • 聚类中心表示类平均特征，可以作为类代表

• 特点

  • 算法性能依赖初始聚类中心，需要依赖其他算法快速确定 初始聚类中心、或多次执行算法
  • 不能确保收敛于最优解

• soft cluster：点可以属于多个类

参数选择

• 聚类数目$C$：$C$远远小于聚类样本总数目，且大于1
• 柔性参数$m$
  • $m$过大：聚类效果差
  • $m$过小：算法接近HCM聚类算法

算法流程

• 标准化数据矩阵
• 建立模糊相似矩阵，初始化隶属矩阵

• 迭代，直到目标函数收敛到极小值

  $$w_k(x_i) = \frac 1 \sum_{i=1}^k (\frac {d(x_i, \mu_k)} {d(x_i, \mu_i} )^{1/(m-2)})$$

• 根据迭代结果，由最终隶属矩阵确定数据所属类，得到聚类结果

常见算法、改进

• HCM算法

基于约束的算法

基于约束的算法：考虑聚类问题中的约束条件，利用约束知识进行 推理

• 约束

  • 对聚类参数的约束
  • 对数据点的约束

• 典型算法

  • Clustering with Obstructed Distance：用两点之间障碍 距离取代一般的欧式距离计算最小距离

量子聚类

量子聚类：用量子理论解决聚类过程中初值依赖、确定类别数目的 问题

• 典型算法
  • 基于相关点的Pott自旋、统计机理提供的量子聚类模型： 将聚类问题视为物理系统

核聚类

核聚类：增加对样本特征的优化过程，利用Mercer核把输入空间映射 至高维特征空间，在特征空间中进行聚类

• 特点

  • 方法普适
  • 性能上优于经典聚类算算法
  • 可以通过非线性映射较好分辨、提取、放大有用特征
  • 收敛速度快

• 典型算法

  • SVDD算法
  • SVC算法

谱聚类

谱聚类：建立在图论中谱图理论基础上，本质是将聚类问题转换为 图的最优划分问题

基本流程

• 根据样本数据集定义描述成对数据点的相似度亲和矩阵
• 计算矩阵特征值、特征向量
• 选择合适的特征向量聚类不同点