Entropy

• （信息）熵：在概率分布上对复杂程度/多样性/不确定性/混乱程度的度量

$$\begin{align*} HOD(X) & = -E_P log P(x) \\ & = \sum_d^D P(x_d) log \frac 1 {P(x_d)} \\ & = - \sum_d^D p_d log p_d \\ \end{align*}$$

• $p_d$：随机变量各取值对应概率
• 事件 $i$ 发生概率 $p_d=0$：约定 $p_d log(p_d)$ 为 0
• 其中 $log$ 以 2 为底，单位为 bit，以 $e$ 为底，单位为 nat

• 信息论中，熵越高能传输越多信息

  • 可携带的信息量 = 单位消息熵 * 消息长度
  • 熵衡量系统复杂程度，提高系统确定性即削弱系统多样性，降低熵

• 概率分布包含的信息即其复杂程度（可能取值数量）

  • 考虑按照 $(p_1,\cdots,p_D)$ 分布、长度为 $N$ 的随机变量序列，其可能排列数为 $\frac {N!} {\prod_d^D (p_d N)!}$

  • 则根据 Stirling 公式有

    $$\begin{align*} log (\frac {N!} {\prod_d^D (p_d N)!}) & = log(N!) - \sum_d^D log((p_d N)!) \\ & \overset {\lim_{N \rightarrow \infty}} = log(\sqrt {2\pi N} ({\frac N e})^N) + \sum_d^D log(\sqrt {2\pi p_dN} ({\frac {p_dN} e})^{p_dN}) \\ & = log(\sqrt {2\pi N}) + N(logN-1) - \sum_d^D log(\sqrt {2\pi p_dN}) - \sum_d^D p_dN (log(p_dN) - 1) \\ & = log(\sqrt {2\pi N} + \sum_d^D log(\sqrt {2\pi p_dN})) + N \sum_d^D p_d log p_d \\ & \approx N \sum_d^D p_d log p_d \end{align*}$$

  • 则长度为 $N$ 的随机变量串的多样性、信息量为 $H * N$，其中 $H=\sum_d^D p_d log p_d$ 概率分布的信息熵

• 某个事件包含的信息可以用编码长度理解

  • 对概率 $p$ 事件，编码 $1/p$ 个需编码（2进制编码）长度 $log_2 \frac 1 p$
  • 则概率 $p$ 事件包含信息量可以定义为 $log \frac 1 p$，即事件包含的信息量可用表示事件需要编码的长度表示 （底数则取决于编码元，只影响系数）
  • 则整个随机变量的信息为各事件信息量加权和

• 熵可以视为变量取值概率的加权和

  • 只依赖随机变量 $X$ 的分布，与其取值无关，可将其记为 $H(P)$
  • 由定义 $0 \leq H(P) \leq log_2 k$
    • $H(p) = 0$：$\exists j, p_j=1$，随机变量只能取一个值，无不确定性
    • $H(p) = log k$：$\forall j, p_j=1/k$，随机变量在任意取值概率相等，不确定性最大

• empirical entropy：经验熵，熵中的概率由数据估计时（尤极大似然估计）
• 参考链接

  • https://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)
  • https://zhuanlan.zhihu.com/p/27876027
  • https://zhuanlan.zhihu.com/p/73710585

• Stirling 公式即用积分近似计算 $\sum logn$：https://zhuanlan.zhihu.com/p/143992660

熵的性质

• 对称性：事件取值不影响熵

• 极值性

  • 所有符号有同等机会出现的情况下，熵达到极大（琴生不等式）

    $$\begin{align*} H(X) & = E[log(\frac 1 {P(X)})] \leq log(E[\frac 1 {P(x)}]) & = log(n) \end{align*}$$

  • 仅有一个符号确定出现的情况下，熵达到极小 0

• Continuity连续性：度量连续，概率微小变化只能引起熵微小变化

• Normalization规范化：$H_2(\frac 1 2, \frac 1 2) = 1$

• Grouping组合法则/可加和性：熵与过程如何划分无关 （此即要求熵形式为对数）

  • 若子系统间相互作用已知，则可以通过子系统熵值计算系统整体熵

    $$H(X) = H(X_1,\cdots,X_K) + \sum_{k=1}^K \frac {|X_k|} {|X|} H(X_k)$$

    • $X_1,\cdots,X_K$：$K$ 个子系统，可以理解为将随机变量 $X$ 划分为 $K$ 种情况
    • $H(X_1,\cdots,X_K)$：子系统相互作用熵

    • 子系统相互作用熵可以认为是，通过已知信息消除的多样性（即信息增益）
    • 子系统熵之和则是利用已知信息消除多样性之后，系统剩余混乱程度

  • 一般的，两个事件 $X,Y$ 熵满足以下计算关系

    $$\begin{align*} H(X, Y) & = H(X) + H(Y|X) \\ & = H(Y) + H(X|Y) \\ & \leqslant H(X) + H(Y) \\ H(X|Y) & \leqslant H(X) \\ \end{align*}$$

  • 特别的，若事件 $X, Y$ 相互独立

    $$\begin{align*} H(X|Y) &= H(X) \\ H(X, Y) &= H(X) + H(Y) \end{align*}$$

• 满足以上特性的熵定义必然为如下形式

$$
-K \sum P(x)log(P(x))
$$

• 在热力学、信息论等领域，熵有多种不同定义，满足熵性质的测度泛函，只能具有（Shannon 熵和 Hartley 熵）或（von Neumann 熵和 Shannon 熵）线性组合的函数形式，若不要求满足组合法则，还有 Tsallis 熵等

Conditinal Entropy

条件熵：随机变量 $X$ 给定条件下，随机变量 $Y$ 的条件概率分布的熵对 $X$ 的数学期望

$$\begin{align*} H(Y|X) & = \sum_{i=1}^N p_i H(Y|X=x_i) \\ H(Y|x=x_i) & = - \sum_j P(y_j|x_i) log P(y_j|x_i) \end{align*}$$

• $P(X=xi, Y=y_j)=p{i,j}$：随机变量 $(X,Y)$ 联合概率分布
• $p_i=P(X=x_i)$
• $H(Y|X=x_i)$：后验熵

• 特别的，考虑数据集 $D$ 被分为 $D_1,\cdots,D_m$，条件经验熵可计算如下

  $$\begin{align*} H(D|A) & = \sum_{m=1}^M \frac {|D_m|} {|D|} H(D_m) \\ & = -\sum_{m=1}^M \frac {|D_m|} {|D|} \sum_{k=1}^K \frac {|D_{m,k}|} {|D_m|} log_2 \frac {|D_{m,k}|} {|D_m|} \end{align*}$$

• postorior entropy：后验熵，随机变量 $X$ 给定条件下，随机变量 $Y$ 的条件概率分布的熵
• empirical conditional entropy：经验条件熵，概率由数据估计

Infomation Gain/Mutual Infomation

互信息/信息增益：（经验）熵与（经验）条件熵之差

$$\begin{align*} g(Y|X) & = H(Y) - H(Y|X) \\ & = \sum_{x \in X} \sum_{y \in Y} P(x,y) log \frac {P(x,y)} {P(x)P(y)} \end{align*}$$

• 与数据集具体分布有关、与具体取值无关

  • 绝对大小同易受熵影响，（经验）熵较大时，互信息也相对较大
  • 由于误差存在，分类取值数目较多者信息增益较大

• 可衡量变量 $X$ 对 $Y$ 预测能力、减少不确定性的能力

  • 信息增益越大，变量之间相关性越强，自变量预测因变量能力越强
  • 只能考察特征对整个系统的贡献，无法具体到特征某个取值
  • 只适合作全局特征选择，即所有类使用相同的特征集合

Infomation Gain Ratio

信息增益比：信息增益对原始信息熵的比值

$$\begin{align*} g_R(Y|X) & = \frac {g(Y|X)} {H(X)} \end{align*}$$

• 考虑熵大小，减弱熵绝对大小的影响

Cross Entropy

• 信息论：基于相同事件测度的两个概率分布 $P, Q$，基于非自然（相较于真实分布 $P$）概率分布 $Q$ 进行编码，在事件集合中唯一标识事件所需 bit
• 概率论：概率分布 $P, Q$ 之间差异

$$\begin{align*} H(P, Q) & = E_P[-log Q] = \left \{ \begin{array}{l} -\sum_{X} P(x) logQ(x), & 离散分布 \\ -\int_X P(x) log(Q(x)) d(r(x)), & 连续分布 \end{array} \right. \\ & = H(P) + D_{KL}(P||Q) \end{align*}$$

• $P(x), Q(x)$：概率分布（密度）函数
• $r(x)$：测度，通常是 $Borel \sigma$ 代数上的勒贝格测度
• $D_{KL}(P||Q)$：$P$ 到 $Q$ 的 KL 散度（$P$ 相对于 $Q$ 的相对熵）

• 信息论中，交叉熵可以看作是信息片段在错误分布 $Q$ 分布下的期望编码长度
  • 信息实际分布实际为 $P$，所以期望基于 $P$

• 交叉熵是常用的损失函数：效果等价于 KL 散度，但计算方便
• sigmoid 激活函数时：相较于二次损失，收敛速度更快

Entropy 衍生指标

Kullback-Leibler Divergence

KL 散度/相对熵：衡量概率分布 $P, Q$ 之间差异的量化指标

$$\begin{align*} D_{KL}(P||Q) & = E_P[(-log Q(x)) - (-log P(x))] \\ & = E_P[log P(x) - log Q(x)] \\ & = \sum_{d=1}^D P(x_d) (log P(x_d) - log Q(x_d)) \\ & = \sum_{d=1} P(x_d) log \frac {P(x_d)} {Q(x_d)} \end{align*}$$

• KL 散度含义

  • 原始分布 $P$、近似分布 $Q$ 之间对数差值期望
  • 若使用观察分布 $Q$ 描述真实分布 $P$，还需的额外信息量

• KL 散度不对称，分布 $P$ 度量 $Q$、$Q$ 度量 $P$ 损失信息不同

  • 从计算公式也可以看出
  • KL散度不能作为不同分布之间距离的度量

Population Stability Index

PSI：衡量分布 $P, Q$ 之间的差异程度

$$\begin{align*} PSI &= \sum_d^D (P_d - Q_d) * log \frac {P_d} {Q_d} \\ &= \sum_d^D P_d log \frac {P_d} {Q_d} + \sum_d^D Q_d log \frac {Q_d} {P_d} \\ &= D_{KL}(P||Q) + D_{KL}(Q||P) \end{align*}$$

• 是 KL 散度的对称操作
  • 更全面的描述两个分布的差异

Gini 指数

基尼指数：可视为信息熵的近似替代

$$\begin{align*} Gini(p) & = \sum_{k=1}^K p_k(1-p_k) \\ & = 1 - \sum_{k=1}^K p_k^2 \end{align*}$$

• $p$：概率分布
• 异质性最小：Gini 系数为 0
• 异质性最大：Gini 系数为 $1 - \frac 1 k$

• Gini 指数度量分布的不纯度
  • 包含类别越多，Gini 指数越大
  • 分布越均匀，Gini 指数越大

• 熵较 Gini 指数对不纯度判罚更重

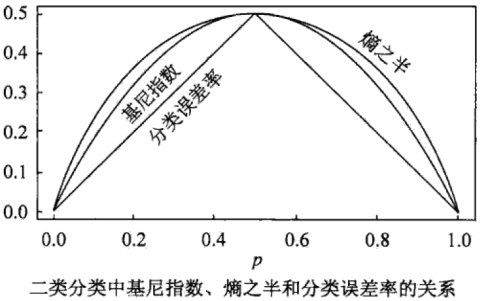
• 经济学领域的 Gini 系数更类似 AUC 值

与 Entropy 关系

$$\begin{align*} H(X) & = -E_P log P(x) \\ & = - \sum_i^N p_i log p_i \\ & = - \sum_i^N p_i (log (1 + (p_i-1))) \\ & = - \sum_i^N p_i (p_i - 1 + \xi(p_i^{'}-1)) \\ & \approx 1 - \sum_i^N p_i^2 \end{align*}$$

• Gini 指数可以视为是熵在 1 附近的一阶泰勒展开近似

条件 Gini 指数

$$Gini(Y|X) = \sum_{k=1}^K P(X=x_k)Gini(Y|X=x_k)$$

• 性质类似信息增益

逻辑斯蒂回归

逻辑斯蒂分布

$$\begin{align*} F(x) & = P(X \leq x) = \frac 1 {1 + e^{-(x-\mu)/\gamma}} \\ f(x) & = F^{'}(x) = \frac {e^{-(x-\mu)/\gamma}} {\gamma(1+e^{-(x-\mu)/\gamma})^2} \end{align*}$$

• $\mu$：位置参数
• $\gamma$：形状参数

• 分布函数属于逻辑斯蒂函数

• 分布函数图像为sigmoid curve

  • 关于的$(\mu, \frac 1 2)$中心对称 $$F(-x+\mu) - \frac 1 2 = -F(x+\mu) + \frac 1 2$$
  • 曲线在靠近$\mu$中心附近增长速度快，两端速度增长慢
  • 形状参数$\gamma$越小，曲线在中心附近增加越快

• 模型优点

  • 模型输出值位于0、1之间，天然具有概率意义，方便观测 样本概率分数
  • 可以结合$l-norm$正则化解决过拟合、共线性问题
  • 实现简单，广泛用于工业问题
  • 分类时计算量比较小、速度快、消耗资源少

• 模型缺点

  • 特征空间很大时，性能不是很好，容易欠拟合，准确率一般
  • 对非线性特征需要进行转换

Binomial Logistic Regression Model

二项逻辑斯蒂回归模型：形式为参数化逻辑斯蒂分布的二分类 生成模型

$$\begin{align*} P(Y=1|x) & = \frac {exp(wx + b)} {1 + exp (wx + b)} \\ P(Y=0|x) & = \frac 1 {1 + exp(wx + b)} \\ P(Y=1|\hat x) & = \frac {exp(\hat w \hat x)} {1 + exp (\hat w \hat x)} \\ P(Y=0|\hat x) & = \frac 1 {1+exp(\hat w \hat x)} \end{align*}$$

• $w, b$：权值向量、偏置
• $\hat x = (x^T|1)^T$
• $\hat w = (w^T|b)^T$

• 逻辑回归比较两个条件概率值，将实例$x$归于条件概率较大类

• 通过逻辑回归模型，可以将线性函数$wx$转换为概率

  • 线性函数值越接近正无穷，概率值越接近1
  • 线性函数值越接近负无穷，概率值越接近0

Odds/Odds Ratio

• 在逻辑回归模型中，输出$Y=1$的对数几率是输入x的线性函数

  $$log \frac {P(Y=1|x)} {1-P(Y=1|x)} = \hat w \hat x$$

• OR在逻辑回归中意义：$x_i$每增加一个单位，odds将变为原来 的$e^{w_i}$倍

  $$\begin{align*} odd &= \frac {P(Y=1|x)} {1-P(Y=1|x)} = e^{\hat w \hat x} \\ OR_{x_i+1 / x_i} &= e^{w_i} \end{align*}$$

  • 对数值型变量

    • 多元LR中，变量对应的系数可以计算相应 Conditional OR
    • 可以建立单变量LR，得到变量系数及相应 Marginal OR

  • 对分类型变量

    • 可以直接计算变量各取值间对应的OR
    • 变量数值化编码建立模型，得到变量对应OR

    • 根据变量编码方式不同，变量对应OR的含义不同，其中 符合数值变量变动模式的是WOE线性编码

策略

极大似然：极小对数损失（交叉熵损失）

$$\begin{align*} L(w) & = log \prod_{i=1}^N [\pi(x_i)]^{y_i} [1-\pi(x_i)]^{1-y_i} \\ & = \sum_{i=1}^N [y_i log \pi(x_i) + (1-y_i)log(1-\pi(x_i))] \\ & = \sum_{i=1}^N [y_i log \frac {\pi(x_i)} {1-\pi(x_i)} log(1-\pi(x_i))] \\ & = \sum_{i=1}^N [y_i(\hat w \hat x_i) - log(1+exp(\hat w \hat x_i))] \end{align*}$$

• $\pi(x) = P(Y=1|x)$

算法

• 通常采用梯度下降、拟牛顿法求解有以上最优化问题

Multi-Nominal Logistic Regression Model

多项逻辑斯蒂回归：二项逻辑回归模型推广

$$\begin{align*} P(Y=j|x) & = \frac {exp(\hat w_j \hat x)} {1+\sum_{k=1}^{K-1} exp(\hat w_k \hat x)}, k=1,2,\cdots,K-1 \\ P(Y=K|x) & = \frac 1 {1+\sum_{k=1}^{K-1} exp(\hat w_k \hat x)} \end{align*}$$

• 策略、算法类似二项逻辑回归模型

Generalized Linear Model

todo

Maximum Entropy Model

最大熵原理

最大熵原理：学习概率模型时，在所有可能的概率模型（分布）中， 熵最大的模型是最好的模型

• 使用约束条件确定概率模型的集合，则最大熵原理也可以表述为 在满足约束条件的模型中选取熵最大的模型

• 直观的，最大熵原理认为

  • 概率模型要满足已有事实（约束条件）
  • 没有更多信息的情况下，不确定部分是等可能的
  • 等可能不容易操作，所有考虑使用可优化的熵最大化 表示等可能性

最大熵模型

最大熵模型为生成模型

• 对给定数据集$T={(x_1,y_1),\cdots,(x_N,y_N)}$，联合分布 P(X,Y)、边缘分布P(X)的经验分布如下

  $$\begin{align*} \tilde P(X=x, Y=y) & = \frac {v(X=x, Y=y)} N \\ \tilde P(X=x) & = \frac {v(X=x)} N \end{align*}$$

  • $v(X=x,Y=y)$：训练集中样本$(x,y)$出频数

• 用如下feature function $f(x, y)$描述输入x、输出y之间 某个事实

  $$f(x, y) = \left \{ \begin{array}{l} 1, & x、y满足某一事实 \\ 0, & 否则 \end{array} \right.$$

  • 特征函数关于经验分布$\tilde P(X, Y)$的期望

    $$E_{\tilde P} = \sum_{x,y} \tilde P(x,y)f(x,y)$$

  • 特征函数关于生成模型$P(Y|X)$、经验分布$\tilde P(X)$ 期望

    $$E_P(f(x)) = \sum_{x,y} \tilde P(x)P(y|x)f(x,y)$$

• 期望模型$P(Y|X)$能够获取数据中信息，则两个期望值应该相等

  $$\begin{align*} E_P(f) & = E_{\tilde P}(f) \\ \sum_{x,y} \tilde P(x)P(y|x)f(x,y) & = \sum_{x,y} \tilde P(x,y)f(x,y) \end{align*}$$

  此即作为模型学习的约束条件

  • 此约束是纯粹的关于$P(Y|X)$的约束，只是约束形式特殊， 需要通过期望关联熵

  • 若有其他表述形式、可以直接带入的、关于$P(Y|X)$约束， 可以直接使用

• 满足所有约束条件的模型集合为 $$\mathcal{C} = \{P | E_{P(f_i)} = E_{\tilde P (f_i)}, i=1,2,\cdots,n \}$$ 定义在条件概率分布$P(Y|X)$上的条件熵为 $$H(P) = -\sum_{x,y} \tilde P(x) P(y|x) logP(y|x)$$ 则模型集合$\mathcal{C}$中条件熵最大者即为最大是模型

策略

最大熵模型的策略为以下约束最优化问题

$$\begin{array}{l} \max_{P \in \mathcal{C}} & -H(P)=\sum_{x,y} \tilde P(x) P(y|x) logP(y|x) \\ s.t. & E_P(f_i) - E_{\tilde P}(f_i) = 0, i=1,2,\cdots,M \\ & \sum_{y} P(y|x) = 1 \end{array}$$

• 引入拉格朗日函数

  $$\begin{align*} L(P, w) & = -H(P) - w_0(1-\sum_y P(y|x)) + \sum_{m=1}^M w_m(E_{\tilde P}(f_i) - E_P(f_i)) \\ & = \sum_{x,y} \tilde P(x) P(y|x) logP(y|x) + w_0 (1-\sum_y P(y|x)) + \sum_{m=1}^M w_m (\sum_{x,y} \tilde P(x,y)f_i(x, y) - \tilde P(x)P(y|x)f_i(x,y)) \end{align*}$$

  • 原始问题为

    $$\min_{P \in \mathcal{C}} \max_{w} L(P, w)$$

  • 对偶问题为

    $$\max_{w} \min_{P \in \mathcal{C}} L(P, w)$$

  • 考虑拉格朗日函数$L(P, w)$是P的凸函数，则原始问题、 对偶问题解相同

• 记

  $$\begin{align*} \Psi(w) & = \min_{P \in \mathcal{C}} L(P, w) = L(P_w, w) \\ P_w & = \arg\min_{P \in \mathcal{C}} L(P, w) = P_w(Y|X) \end{align*}$$

• 求$L(P, w)$对$P(Y|X)$偏导

  $$\begin{align*} \frac {\partial L(P, w)} {\partial P(Y|X)} & = \sum_{x,y} \tilde P(x)(logP(y|x)+1) - \sum_y w_0 - \sum_{x,y}(\tilde P(x) \sum_{i=1}^N w_i f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x)(log P(y|x) + 1 - w_0 - \sum_{i=1}^N w_i f_i(x, y)) \end{align*}$$

  偏导置0，考虑到$\tilde P(x) > 0$，其系数必始终为0，有

  $$\begin{align*} P(Y|X) & = \exp(\sum_{i=1}^N w_i f_i(x,y) + w_0 - 1) \\ & = \frac {exp(\sum_{i=1}^N w_i f_i(x,y))} {exp(1-w_0)} \end{align*}$$

• 考虑到约束$\sum_y P(y|x) = 1$，有

  $$\begin{align*} P_w(y|x) & = \frac 1 {Z_w(x)} exp(\sum_{i=1}^N w_i f_i(x,y)) \\ Z_w(x) & = \sum_y exp(\sum_{i=1}^N w_i f_i(x,y)) \\ & = exp(1 - w_0) \end{align*}$$

  • $Z_w(x)$：规范化因子
  • $f(x, y)$：特征
  • $w_i$：特征权值

• 原最优化问题等价于求解偶问题极大化问题$\max_w \Psi(w)$

  $$\begin{align*} \Psi(w) & = \sum_{x,y} \tilde P(x) P_w(y|x) logP_w(y|x) + \sum_{i=1}^N w_i(\sum_{x,y} \tilde P(x,y) f_i(x,y) - \sum_{x,y} \tilde P(x) P_w(y|x) f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) + \sum_{x,y} \tilde P(x,y) P_w(y|x)(log P_w(y|x) - \sum_{i=1}^N w_i f_i(x,y)) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_{x,y} \tilde P(x,y) P_w(y|x) log Z_w(x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_x \tilde P(x) log Z_w(x) \end{align*}$$

  记其解为

  $$w^{*} = \arg\max_w \Psi(w)$$

  带入即可得到最优（最大熵）模型$P_{w^{*}}(Y|X)$

策略性质

• 已知训练数据的经验概率分布为$\tilde P(X,Y)$，则条件概率 分布$P(Y|X)$的对数似然函数为

  $$\begin{align*} L_{\tilde P}(P_w) & = N log \prod_{x,y} P(y|x)^{\tilde P(x,y)} \\ & = \sum_{x,y} N * \tilde P(x,y) log P(y|x) \end{align*}$$

  • 这里省略了系数样本数量$N$

• 将最大熵模型带入，可得

  $$\begin{align*} L_{\tilde P_w} & = \sum_{x,y} \tilde P(y|x) logP(y|x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_{x,y} \tilde P(x,y)log Z_w(x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^N w_i f_i(x,y) - \sum_x \tilde P(x) log Z_w(x) \\ & = \Psi(w) \end{align*}$$

  对偶函数$\Psi(w)$等价于对数似然函数$L_{\tilde P}(P_w)$， 即最大熵模型中，对偶函数极大等价于模型极大似然估计

改进的迭代尺度法

• 思想

  • 假设最大熵模型当前参数向量$w=(w_1,w_2,\cdots,w_M)^T$
  • 希望能找到新的参数向量（参数向量更新） $w+\sigma=(w_1+\sigma_1,\cdots,w_M+\sigma_M)$ 使得模型对数似然函数/对偶函数值增加
  • 不断对似然函数值进行更新，直到找到对数似然函数极大值

• 对给定经验分布$\tilde P(x,y)$，参数向量更新至$w+\sigma$ 时，对数似然函数值变化为

  $$\begin{align*} L(w+\sigma) - L(w) & = \sum_{x,y} \tilde P(x,y) log P_{w+\sigma}(y|x) - \sum_{x,y} \tilde P(x,y) log P_w(y|x) \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) - \sum_x \tilde P(x) log \frac {Z_{w+\sigma}(x)} {Z_w(x)} \\ & \geq \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \frac {Z_{w+\sigma}(x)} {Z_w(x)} \\ & = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_y(y|x) exp(\sum_{i=1}^M \sigma_i f_i(x,y)) \end{align*}$$

  • 不等式步利用$a - 1 \geq log a, a \geq 1$

  • 最后一步利用

    $$\begin{align*} \frac {Z_{w+\sigma}(x)} {Z_w(x)} & = \frac 1 {Z_w(x)} \sum_y exp(\sum_{i=1}^M (w_i + \sigma_i) f_i(x, y)) \\ & = \frac 1 {Z_w(x)} \sum_y exp(\sum_{i=1}^M w_i f_i(x,y) + \sigma_i f_i(x,y)) \\ & = \sum_y P_w(y|x) exp(\sum_{i=1}^n \sigma_i f_i(x,y)) \end{align*}$$

• 记上式右端为$A(\sigma|w)$，则其为对数似然函数改变量的 一个下界

  $$L(w+\sigma) - L(w) \geq A(\sigma|w)$$
  • 若适当的$\sigma$能增加其值，则对数似然函数值也应该 增加
  • 函数$A(\sigma|w)$中因变量$\sigma$为向量，难以同时 优化，尝试每次只优化一个变量$\sigma_i$，固定其他变量 $\sigma_j$

• 记

  $$f^{**} (x,y) = \sum_i f_i(x,y)$$

  考虑到$f_i(x,y)$为二值函数，则$f^{**}(x,y)$表示所有特征 在$(x,y)$出现的次数，且有

  $$A(\sigma|w) = \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_w(y|x) exp(f^{**}(x,y) \sum_{i=1}^M \frac {\sigma_i f_i(x,y)} {f^{**}(x,y)})$$

• 考虑到$\sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} = 1$， 由指数函数凸性、Jensen不等式有

  $$exp(\sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} \sigma_i f^{**}(x,y)) \leq \sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} exp(\sigma_i f^{**}(x,y))$$

  则

  $$A(\sigma|w) \geq \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M \sigma_i f_i(x,y) + 1 - \sum_x \tilde P(x) \sum_y P_w(y|x) \sum_{i=1}^M \frac {f_i(x,y)} {f^{**}(x,y)} exp(\sigma_i f^{**}(x,y))$$

• 记上述不等式右端为$B(\sigma|w)$，则有

  $$L(w+\sigma) - L(w) \geq B(\sigma|w)$$

  其为对数似然函数改变量的一个新、相对不紧的下界

• 求$B(\sigma|w)$对$\sigma_i$的偏导

  $$\frac {\partial B(\sigma|w)} {\partial \sigma_i} = \sum_{x,y} \tilde P(x,y) f_i(x,y) - \sum_x \tilde P(x) \sum_y P_w(y|x) f_i(x,y) exp(\sigma_i f^{**}(x,y))$$

  置偏导为0，可得

  $$\sum_x \tilde P(x) \sum_y P_w(y|x) f_i(x,y) exp(\sigma_i f^{**}(x,y)) = \sum_{x,y} \tilde P(x,y) f_i(x,y) = E_{\tilde P}(f_i)$$

  其中仅含变量$\sigma_i$，则依次求解以上方程即可得到 $\sigma$

算法

• 输入：特征函数$f_1, f_2, \cdots, f_M$、经验分布 $\tilde P(x)$、最大熵模型$P_w(x)$
• 输出：最优参数值$wi^{*}$、最优模型$P{w^{*}}$

1. 对所有$i \in {1,2,\cdots,M}$，取初值$w_i = 0$

2. 对每个$i \in {1,2,\cdots,M}$，求解以上方程得$\sigma_i$

   • 若$f^{**}(x,y)=C$为常数，则$\sigma_i$有解析解

     $$\sigma_i = \frac 1 C log \frac {E_{\tilde P}(f_i)} {E_P(f_i)}$$

   • 若$f^{**}(x,y)$不是常数，则可以通过牛顿法迭代求解

     $$\sigma_i^{(k+1)} = \sigma_i^{(k)} - \frac {g(\sigma_i^{(k)})} {g^{'}(\sigma_i^{(k)})}$$

     • $g(\sigma_i)$：上述方程对应函数

     • 上述方程有单根，选择适当初值则牛顿法恒收敛

3. 更新$w_i$，$w_i \leftarrow w_i + \sigma_i$，若不是所有 $w_i$均收敛，重复2

BFGS算法

对最大熵模型

• 为方便，目标函数改为求极小

  $$\begin{array}{l} \min_{w \in R^M} f(w) = \sum_x \tilde P(x) log \sum_{y} exp(\sum_{i=1}^M w_i f_i(x,y)) - \sum_{x,y} \tilde P(x,y) \sum_{i=1}^M w_i f_i(x,y) \end{array}$$

• 梯度为

  $$\begin{align*} g(w) & = (\frac {\partial f(w)} {\partial w_i}, \cdots, \frac {\partial f(w)} {\partial w_M})^T \\ \frac {\partial f(w)} {\partial w_M} & = \sum_{x,y} \tilde P(x) P_w(y|x) f_i(x,y) - E_{\tilde P}(f_i) \end{align*}$$

算法

将目标函数带入BFGS算法即可

• 输入：特征函数$f_1, f_2, \cdots, f_M$、经验分布 $\tilde P(x)$、最大熵模型$P_w(x)$
• 输出：最优参数值$wi^{*}$、最优模型$P{w^{*}}$

1. 取初值$w^{(0)}$、正定对称矩阵$B^{(0)}$，置k=0

2. 计算$g^{(k)} = g(w^{(k)})$，若$|g^{(k)}| < \epsilon$， 停止计算，得到解$w^{*} = w^{(k)}$

3. 由拟牛顿公式$B^{(k)}p^{(k)} = -g^{(k)}$求解$p^{(k)}$

4. 一维搜索，求解

   $$\lambda^{(k)} = \arg\min_{\lambda} f(w^{(k)} + \lambda p_k)$$

5. 置$w^{(k+1)} = w^{(k)} + \lambda^{(k)} p_k$

6. 计算$g^{(k+1)} = g(w^{(k+1)})$，若 $|g^{(k+1)}| < \epsilon$，停止计算，得到解 $w^{*} = w^{(k+1)}$，否则求

   $$B^{(k+1)} = B^{(k)} - \frac {B^{(k)} s^{(k)} (s^{(k)})^T B^{(k)}} {(s^{(k)})^T B^{(k)} s^{(k)}} + \frac {y^{(k)} (y^{(k)})^T} {(y^{(k)})^T s^{(k)}}$$

   • $s^{(k)} = w^{(k+1)} - w^{(k)}$
   • $y^{(k)} = g^{(k+1)} - g^{(k)}$

7. 置k=k+1，转3

总述

expectation maximization algorithm：含有隐变量的概率模型 参数的极大似然估计法、极大后验概率估计法

• 模型含有latent variable（潜在变量）、hidden variable （隐变量）似然函数将没有解析解

• 所以EM算法需要迭代求解，每次迭代由两步组成

  • E步：求期望expectation
  • M步：求极大maximization

• 模型变量都是observable variable、给定数据情况下，可以 直接使用极大似然估计、贝叶斯估计

EM算法

对含有隐变量的概率模型，目标是极大化观测数据（不完全数据） $Y$关于参数$\theta$的对数似然函数，即极大化

$$\begin{align*} L(\theta) & = log P(Y|\theta) \\ & = log \sum_Z P(Y, Z|\theta) \\ & = log \left(\sum_Z P(Y|Z,\theta) P(Z|\theta) \right) \end{align*}$$

• $Y$：观测变量数据
• $Z$：隐随机变量数据（未知）
• $Y,Z$合在一起称为完全数据
• $P(Y,Z|\theta)$：联合分布
• $P(Z|Y,\theta)$：条件分布

• 但是极大化目标函数中包括未观测数据$Z$、求和（积分）的 对数，直接求极大化非常困难
• EM算法通过迭代逐步近似极大化$L(\theta)$

推导

• 假设第i次迭代后$\theta$的估计值是$\theta^{(i)}$，希望 新估计值$\theta$能使$L(\theta)$增加，并逐步增加到极大值 ，考虑两者之差

  $$L(\theta) - L(\theta^{(i)}) = log (\sum_Z P(Y|Z,\theta) P(Z|\theta)) - log P(Y|\theta^{(i)})$$

• 利用Jensen不等式有

  $$\begin{align*} L(\theta) - L(|\theta^{(i)}) & = log(\sum_Z P(Y|Z, \theta^{(i)}) \frac {P(Y|Z,\theta) P(Z|\theta)} {P(Y|Z,\theta^{(i)})}) - log P(Y|\theta^{(i)}) \\ & \geq \sum_Z P(Z|Y,\theta^{(i)}) log \frac {P(Y|Z,\theta) P(Z|\theta)} {P(Z|Y,\theta^{(i)})} - log P(Y|\theta^{(i)}) \\ & = \sum_z P(Z|Y,\theta^{(i)}) log \frac {P(Y|Z,\theta) P(Z|\theta)} {P(Z|Y,\theta^{(i)}) P(Y|\theta^{(i)})} \end{align*}$$

• 令

  $$B(\theta, \theta^{(i)}) = L(\theta^{(i)}) + \sum_Z P(Z|Y,\theta^{(i)}) log \frac {P(Y|Z,\theta) P(Z|\theta)} {P(Z|Y,\theta^{(i)}) P(Y|\theta^{(i)})}$$

  则$B(\theta, \theta^{(i)})$是$L(\theta)$的一个下界，即

  $$\begin{align*} L(\theta) & \geq B(\theta, \theta^{(i)}) \\ \end{align*}$$

  并根据$B(\theta, \theta^{(i)})$定义有

  $$\begin{align*} L(\theta^{(i)}) = B(\theta^{(i)}, \theta^{(i)}) \end{align*}$$

• 则任意$\theta$满足 $B(\theta,\theta^{(i)}) > B(\theta^{(i)},\theta^{(i)})$ ，将满足$L(\theta) > L(\theta^{(i)})$，应选择 $\theta^{(i+1)}$使得$B(\theta,\theta^{(i)})$达到极大

  $$\begin{align*} \theta^{(i+1)} & = \arg\max_{\theta} B(\theta,\theta^{(i)}) \\ & = \arg\max_{\theta} L(\theta^{(i)}) + \sum_Z P(Z|Y,\theta^{(i)}) log \frac {P(Y|Z,\theta) P(Z|\theta)} {P(Z|Y,\theta^{(i)}) P(Y|\theta^{(i)})} \\ & = \arg\max_{\theta} (\sum_Z P(Z|Y,\theta^{(i)}) log(P(Y|Z,\theta)P(Z|\theta))) \\ & = \arg\max_{\theta} (\sum_Z P(Z|Y,\theta^{(i)}) log P(Y,Z|\theta)) \\ & = \arg\max_{\theta} Q(\theta, \theta^{(i)}) \end{align*}$$

  • 和$\theta$无关的常数项全部舍去

• $Q(\theta, \theta^{(i)})$：Q函数，完全数据的对数似然函数 $logP(Y,Z|\theta)$，关于在给定观测$Y$和当前参数 $\theta^{(i)}$下，对未观测数据Z的条件概率分布 $P(Z|Y,\theta^{(i)})$ $$Q(\theta, \theta^{(i)}) = E_z [logP(Y,Z|\theta)|Y,\theta^{(i)}]$$

算法

1. 选择参数初值$\theta^{0}$，开始迭代

2. E步：记$\theta^{(i)}$为第$i$迭代时，参数$\theta$的估计值 ，在第$i+1$步迭代的E步时，计算Q函数 $Q(\theta, \theta^{(i)})$

3. M步：求使得Q函数极大化$\theta$作为第$i+1$次估计值 $\theta^{(i+1)}$

   $$\theta^{(i+1)} = \arg\max_{\theta} Q(\theta, \theta^{(i)})$$

4. 重复E步、M步直到待估参数收敛

• 算法初值可以任意选择，但EM算法对初值敏感

• E步：参数值估计缺失值分布，计算Q函数（似然函数）

• M步：Q函数取极大得新参数估计值

• 收敛条件一般是对较小正数$\epsilon$，满足 $|\theta^{(i+1)} - \theta^{(i)}| < \epsilon$或 $|Q(\theta^{(i+1)},\theta^{(i)}) - Q(\theta^{(i)},\theta^{(i)})| < \epsilon$

EM算法特点

EM算法优点

• EM算法可以用于估计含有隐变量的模型参数
• 非常简单，稳定上升的步骤能非常可靠的找到最优估计值
• 应用广泛，能应用在多个领域中
  • 生成模型的非监督学习

EM算法缺点

• EM算法计算复杂、受外较慢，不适合高维数据、大规模数据集
• 参数估计结果依赖初值，不够稳定，不能保证找到全局最优解

算法收敛性

定理1

• 设$P(Y|\theta)$为观测数据的似然函数，$\theta^{(i)}$为 EM算法得到的参数估计序列，$P(Y|\theta^{(i)}),i=1,2,…$ 为对应的似然函数序列，则$P(Y|\theta^{(i)})$是单调递增的 $$P(Y|\theta^{(i+1)}) \geq P(Y|\theta^{(i)})$$

• 由条件概率

  $$\begin{align*} P(Y|\theta) & = \frac {P(Y,Z|\theta)} {P(Z|Y,\theta)} \\ logP(Y|\theta) & = logP(Y,Z|\theta) - logP(Z|Y,\theta) \end{align*}$$

• 则对数似然函数有

  $$logP(Y|\theta) = Q(\theta, \theta^{(i)}) - H(\theta, \theta^{(i)})$$

  • $H(\theta, \theta^{(i)}) = \sum_Z log P(Z|Y,\theta) P(Z|Y,\theta)$
  • $Q(\theta, \theta^{(i)})$：前述Q函数
  • $logP(Y|\theta)$和$Z$无关，可以直接提出

• 分别取$\theta^{(i+1)}, \theta^{(i)}$带入，做差

  $$logP(Y|\theta^{(i+1)}) - logP(Y|\theta^{(i)}) = [Q(\theta^{(i+1)}, \theta^{(i)}) - Q(\theta^{(i)}, \theta^{(i)}] - [H(\theta^{(i+1)}, \theta^{(i)}) - H(\theta^{(i)}, \theta^{(i)})]$$

  • $\theta^{(i+1)}$使得$Q(\theta, \theta^{(i)})$取极大

  • 又有

    $$\begin{align*} & H(\theta^{(i+1)}, \theta^{(i)}) - H(\theta^{(i)}, \theta^{(i)}) \\ = & \sum_Z (log \frac {P(Z|Y,\theta^{(i+1)})} {P(Z|Y,\theta^{(I)})}) P(Z|Y,\theta^{(i)}) \\ \leq & log (\sum_Z \frac {P(Z|Y,\theta^{(i+1)})} {P(Z|Y,\theta^{(I)})} P(Z|Y,\theta^{(i)})) \\ = & log \sum_Z P(Z|Y,\theta^{(i+1)}) = 0 \end{align*}$$

定理2

• 设$L(\theta)=log P(Y|\theta)$为观测数据的对数似然函数， $\theta^{(i)},i=1,2,…$为EM算法得到的参数估计序列， $L(\theta^{(i)}),i=1,2,…$为对应的对数似然函数序列

  • 若$P(Y|\theta)$有上界，则$L(\theta^{(i)})$收敛到某 定值$L^{*}$
  • Q函数$Q(\theta, \theta^{‘})$与$L(\theta)$满足一定 条件的情况下，由EM算法得到的参数估计序列 $\theta^{(i)}$的收敛值$\theta^{*}$是$L(\theta)$的 稳定点

• 结论1由序列单调、有界显然

• Q函数$Q(\theta, \theta^{‘})$与$L(\theta)$的条件在大多数 情况下是满足的
• EM算法收敛性包含对数似然序列$L(\theta^{(i)})$、参数估计 序列$\theta^{(i)}$的收敛性，前者不蕴含后者
• 此定理只能保证参数估计序列收敛到对数似然序列的稳定点， 不能保证收敛到极大点，可选取多个不同初值迭代，从多个结果 中选择最好的

Gaussion Mixture Model

• 高斯混合模型是指具有如下概率分布模型 $$P(y|\theta) = \sum_{k=1}^K \alpha_k \phi(y|\theta_k)$$

  • $\alphak \geq 0, \sum{k=1}^K \alpha_k=1$：系数
  • $\phi(y|\theta_k)$：高斯分布密度函数
  • $\theta_k=(\mu_k, \sigma_k)$：第k个分模型参数

• 用EM算法估计高斯混合模型参数 $\theta=(\alpha_1,…,\alpha_2,\theta_1,…,\theta_K)$

推导

明确隐变量

明确隐变量，写出完全数据对数似然函数

• 反映观测数据$y_j$来自第k个分模型的数据是未知的

  $$\gamma_{j,k} = \left \{ \begin{array}{l} 1, & 第j个观测来自第k个分模型 \\ 0, & 否则 \end{array} \right.$$

  • $j=1,2,\cdots,N$：观测编号
  • $k=1,2,\cdots,K$：模型编号

• 则完全数据为

  $$(y_j,\gamma_{j,1},\cdots,\gamma_{j,K}), j=1,2,...,N$$

• 完全数据似然函数为

  $$\begin{align*} P(y,\gamma|\theta) & = \prod_{j=1}^N P(y_j,\gamma_{j,1},\cdots,\gamma_{j,N}|\theta) \\ & = \prod_{k=1}^{K} \prod_{j=1}^N [\alpha_k \phi(y_j|\theta_k)]^{\gamma _{j,k}} \\ & = \prod_{k=1}^{K} \alpha_k^{n_k} \prod_{j=1}^N [\phi(y_j|\theta_k)]^{\gamma _{j,k}} \\ \end{align*}$$

  • $nk = \sum{j=1}^{N} \gamma_{j,k}$
  • $\sum_{k=1}^K n_k = N$

• 完全数据的对数似然函数为

  $$logP(y, \gamma|\theta) = \sum_{k=1}^K \left \{ n_k log \alpha_k + \sum_{j=1}^N \gamma_{j,k} [log \frac 1 {\sqrt {2\pi}} - log \sigma_k - \frac 1 {2\sigma_k}(y_j - \mu_k)^2] \right \}$$

E步：确定Q函数

$$\begin{align*} Q(\theta, \theta^{(i)}) & = E_z[logP(y,\gamma|\theta)|Y,\theta^{(i)}] \\ & = E \sum_{k=1}^K \left \{ n_k log\alpha_k + \sum_{j=1}^N \gamma_{j,k} [log \frac 1 {\sqrt {2\pi}} - log \sigma_k - \frac 1 {2\sigma_k}(y_j - \mu_k)^2] \right \} \\ & = \sum_{k=1}^K \left \{ \sum_{k=1}^K (E\gamma_{j,k}) log\alpha_k + \sum_{j=1}^N (E\gamma_{j,k}) [log \frac 1 {\sqrt {2\pi}} - log \sigma_k - \frac 1 {2\sigma_k}(y_j - \mu_k)^2] \right \} \end{align*}$$

• $E\gamma{j,k} = E(\gamma{j,k}|y,\theta)$：记为 $\hat \gamma_{j,k}$

$$\begin{align*} \hat \gamma_{j,k} & = E(\gamma_{j,k}|y,\theta) = P(\gamma_{j,k}|y,\theta) \\ & = \frac {P(\gamma_{j,k}=1, y_j|\theta)} {\sum_{k=1}^K P(\gamma_{j,k}=1,y_j|\theta)} \\ & = \frac {P(y_j|\gamma_{j,k}=1,\theta) P(\gamma_{j,k}=1|\theta)} {\sum_{k=1}^K P(y_j|\gamma_{j,k}=1,\theta) P(\gamma_{j,k}|\theta)} \\ & = \frac {\alpha_k \phi(y_j|\theta _k)} {\sum_{k=1}^K \alpha_k \phi(y_j|\theta_k)} \end{align*}$$

带入可得

$$Q(\theta, \theta^{(i)}) = \sum_{k=1}^K \left\{ n_k log\alpha_k + \sum_{k=1}^N \hat \gamma_{j,k} [log \frac 1 {\sqrt{2\pi}} - log \sigma_k - \frac 1 {2\sigma^2}(y_j - \mu_k)^2] \right \}$$

M步

求新一轮模型参数 $\theta^{(i+1)}=(\hat \alpha_1,…,\hat \alpha_2,\hat \theta_1,…,\hat \theta_K)$

$$\begin{align*} \theta^{(i+1)} & = \arg\max_{\theta} Q(\theta,\theta^{(i)}) \\ \hat \mu_k & = \frac {\sum_{j=1}^N \hat \gamma_{j,k} y_j} {\sum_{j=1}^N \hat \gamma_{j,k}} \\ \hat \sigma_k^2 & = \frac {\sum_{j=1}^N \hat \gamma_{j,k} (y_j - \mu_p)^2} {\sum_{j=1}^N \hat \gamma_{j,k}} \\ \hat \alpha_k & = \frac {n_k} N = \frac {\sum_{j=1}^N \hat \gamma_{j,k}} N \end{align*}$$

• $\hat \theta_k = (\hat \mu_k, \hat \sigma_k^2)$：直接求 偏导置0即可得
• $\hat \alphak$：在$\sum{k=1}^K \alpha_k = 1$条件下求 偏导置0求得

算法

• 输入：观测数据$y_1, y_2,\cdots, y_N$，N个高斯混合模型
• 输出：高斯混合模型参数

1. 取参数初始值开始迭代

2. E步：依据当前模型参数，计算分模型k对观测数据$y_j$响应度

   $$\hat \gamma_{j,k} = \frac {\alpha \phi(y_k|\theta_k)} {\sum_{k=1}^N \alpha_k \phi(y_j|\theta)}$$

3. M步：计算新一轮迭代的模型参数 $\hat mu_k, \hat \sigma_k^2, \hat \alpha_k$

4. 重复2、3直到收敛

• GMM模型的参数估计的EM算法非常类似K-Means算法

  • E步类似于K-Means中计算各点和各聚类中心之间距离，不过 K-Means将点归类为离其最近类，而EM算法则是算期望
  • M步根据聚类结果更新聚类中心

GEM

Maximization-Maximization Algorithm

Free Energy函数

• 假设隐变量数据Z的概率分布为$\tilde P(Z)$，定义分布 $\tilde P$与参数$\theta$的函数$F(\tilde P, \theta)$如下 $$F(\tilde P, \theta) = E_{\tilde P} [log P(Y,Z|\theta)] + H(\tilde P)$$

• $H(\tilde P)=-E_{\tilde P} log \tilde P(Z)$：分布 $\tilde P(Z)$的熵
• 通常假设$P(Y,Z|\theta)$是$\theta$的连续函数，则函数 $F(\tilde P,\theta)$是$\tilde P, \theta$的连续函数

定理1

• 对于固定$\theta$，存在唯一分布$\tilde P\theta$，极大化 $F(\tilde P, \theta)$，这时$\tilde P\theta$由下式给出 $$\tilde P_\theta(Z) = P(Z|Y,\theta)$$ 并且$\tilde P_{\theta}$随$\theta$连续变化

• 对于固定的$\theta$，求使得$F(\tilde P, \theta)$的极大， 构造Lagrange函数

  $$L(\tilde P, \lambda, \mu) = F(\tilde P, \theta) + \lambda(1 - \sum_Z \tilde P(Z)) - \mu \tilde P(Z)$$

  因为$\tilde P(Z)$是概率密度，自然包含两个约束

  $$\left \{ \begin{array}{l} \sum_Z \tilde P(Z) = 1 \\ \tilde P(Z) \geq 0 \end{array} \right.$$

  即Lagrange方程中后两项

• 对$\tilde P(Z)$求偏导，得

  $$\frac {\partial L} {\partial \tilde P(Z)} = log P(Y,Z|\theta) - log \tilde P(Z) - \lambda - \mu$$

  令偏导为0，有

  $$\begin{align*} log P(Y,Z|\theta) - log \tilde P(Z) & = \lambda + \mu \\ \frac {P(Y,Z|\theta)} {\tilde P(Z)} & = e^{\lambda + \mu} \end{align*}$$

• 则使得$F(\tilde P, \theta)$极大的$\tilde P_\theta(Z)$ 应该和$P(Y,Z|\theta)$成比例，由概率密度自然约束有

  $$\tilde P_\theta(Z) = P(Y,Z|\theta)$$

  而由假设条件，$P(Y,Z|\theta)$是$\theta$的连续函数

• 这里概率密度函数$\tilde P(Z)$是作为自变量出现

• 理论上对$\tilde P(Z)$和一般的复合函数求导没有区别， 但$E_{\tilde P}, \sum_Z$使得整体看起来非常不和谐

  $$\begin{align*} E_{\tilde P} f(Z) & = \sum_Z f(Z) \tilde P(Z) \\ & = \int f(Z) d(\tilde P(Z)) \end{align*}$$

定理2

• 若$\tilde P_\theta(Z) = P(Z|Y, \theta)$，则 $$F(\tilde P, \theta) = log P(Y|\theta)$$

定理3

• 设$L(\theta)=log P(Y|\theta)$为观测数据的对数似然函数， $\theta^{(i)}, i=1,2,\cdots$为EM算法得到的参数估计序列， 函数$F(\tilde P,\theta)$如上定义

  • 若$F(\tilde P,\theta)$在$\tilde P^{}, \theta^{}$ 上有局部极大值，则$L(\theta)$在$\theta^{*}$也有局部 最大值
  • 若$F(\tilde P,\theta)$在$\tilde P^{}, \theta^{}$ 达到全局最大，则$L(\theta)$在$\theta^{*}$也达到全局 最大

• 由定理1、定理2有

  $$L(\theta) = logP(Y|\theta) = F(\tilde P_\theta, \theta)$$

  特别的，对于使$F(\tilde P,\theta)$极大$\theta^{8}$有

  $$L(\theta^{*}) = logP(Y|\theta^{*}) = F(\tilde P_\theta^{*}, \theta{*})$$

• 由$\tilde P_\theta$关于$\theta$连续，局部点域内不存在点 $\theta^{}$使得$L(\theta^{}) > L(\theta^{})$，否则 与$F(\tilde P, \theta^{})$矛盾

定理4

• EM算法的依次迭代可由F函数的极大-极大算法实现
• 设$\theta^{(i)}$为第i次迭代参数$\theta$的估计， $\tilde P^{(i)}$为第i次迭代参数$\tilde P$的估计，在第 i+1次迭代的两步为

  • 对固定的$\theta^{(i)}$，求$\tilde P^{(i)}$使得 $F(\tilde P, \theta^{(i)})$极大
  • 对固定的$\tilde P^{(i+1)}$，求$\theta^{(i+1)}$使 $F(\tilde P^{(t+1)}, \theta)$极大化

• 固定$\theta^{(i)}$

  $$\begin{align*} F(\tilde P^{(i+1)}, \theta^{(i)} & = E_{\tilde P^{(t+1)}} [log P(Y,Z|\theta)] + H(\tilde P^{(i+1)}) \\ & = \sum_Z log P(Y,Z|\theta) P(Z|Y,\theta^{(i)}) + H(\tilde P^{(i+1)}) \\ & = Q(\theta, \theta^{(i)}) + H(\tilde P^{(i+1)}) \end{align*}$$

• 则固定$\tilde P^{(i+1)}$求极大同EM算法M步

GEM算法

• 输入：观测数据，F函数
• 输出：模型参数

1. 初始化$\theta^{(0)}$，开始迭代

2. 第i+1次迭代：记$\theta^{(i)}$为参数$\theta$的估计值， $\tilde P^{(i)}$为函数$\tilde P$的估计，求 $\tilde P^{(t+1)}$使$\tilde P$极大化$F(\tilde P,\theta)$

3. 求$\theta^{(t+1)}$使$F(\tilde P^{(t+1)l}, \theta)$极大化

4. 重复2、3直到收敛

次优解代替最优解

• 输入：观测数据，Q函数
• 输出：模型参数

1. 初始化参数$\theta^{(0)}$，开始迭代

2. 第i+1次迭代，记$\theta^{(i)}$为参数$\theta$的估计值， 计算

   $$\begin{align*} Q(\theta, \theta^{(i)}) & = E_Z [ log P(Y,Z|\theta)|Y,\theta^{(i)}] \\ & = \sum_Z P(Z|Y, \theta^{(i)}) log P(Y,Z|\theta) \end{align*}$$

3. 求$\theta^{(i+1)}$使

   $$Q(\theta^{(i+1)}, \theta^{(i)}) > Q(\theta^{(i)}, \theta^{(i)})$$

4. 重复2、3直到收敛

• 有时候极大化$Q(\theta, \theta^{(i)})$非常困难，此算法 仅寻找使目标函数值上升方向

ADMM求次优解

• 输入：观测数据，Q函数
• 输出：函数模型

1. 初始化参数 $\theta^{(0)} = (\theta_1^{(0)},…,\theta_d^{(0)})$， 开始迭代

2. 第i次迭代，记 $\theta^{(i)} = (\theta_1^{(i)},…,\theta_d^{(i)})$， 为参数$\theta = (\theta_1,…,\theta_d)$的估计值，计算

   $$\begin{align*} Q(\theta, \theta^{(i)}) & = E_Z [ log P(Y,Z|\theta)|Y,\theta^{(i)}] \\ & = \sum_Z P(Z|Y, \theta^{(i)}) log P(Y,Z|\theta) \end{align*}$$

3. 进行d次条件极大化

   1. 在$\theta1^{(i)},…,\theta{j-1}^{(i)},\theta_{j+1}^{(i)},…,\theta_d^{(i)}$ 保持不变条件下 ，求使$Q(\theta, \theta^{(i)})$达到极大的 $\theta_j^{(i+1)}$

   2. j从1到d，进行d次条件极大化的，得到 $\theta^{(i+1)} = (\theta_1^{(i+1)},…,\theta_d^{(i+1)})$ 使得

      $$Q(\theta^{(i+1)}, \theta^{(i)}) > Q(\theta^{(i)}, \theta^{(i)})$$

4. 重复2、3直到收敛