Vector
向量
- 线性组合
- 向量空间
- 空间的基:向量空间的一组基是张成该空间的一个线性无关向量集
- 线性相关

向量点积
向量点积性质
向量的数乘等比例影响点积,则可为每个向量找到共线单位向量满足 $u \cdot u=1$

点积等同于向量 $b$ 左乘矩阵 $a^T$,即把向量 $b$ 压缩(线性变换)至向量 $a$ 方向上

点积 $a \cdot b$ 与投影关系(假设向量 $a$ 为单位向量)
投影,即将向量 $b$ 线性变换 至 $a$ 方向上的标量
- 则投影可以用 $1 * n$ 矩阵表示
- 投影代表的矩阵则可通过利用基向量的变换结果求解

向量 $a$ 本身作为单位向量
- 坐标轴上单位向量与 $a$ 的内积即为 $a$ 该方向分量,也即 $a$ 在该轴上投影
- 由对称性显然,坐标轴在 $a$ 方向投影等于 $a$ 在轴方向投影
- 则投影到向量 $a$ 代表的线性变换矩阵即为 $a^T$

扩展到一般情况
- 考虑标量乘法对点积影响,坐标轴上向量与任意向量 $a$ 内积等价于投影
- 投影是线性变换,则对空间一组基的变换可以推导到空间中任意向量 $b$
- 高维空间到标量的线性变换与空间中一个向量对应,即应用线性变换等价于同该向量点积
点积用途
- 向量证明基本都是都转换到点积上
- 正定:行列式恒>0
- 下降方向:内积<0
- 方向(趋于)垂直:内积趋于0
求和、积分、点积、卷积
| 连续(函数) | 离散(向量) | |
|---|---|---|
| 单元累计 | 积分:按值出现频率加权求和 | 求和:向量视为分段函数积分 |
| 二元累计 | 卷积:连续卷积 | 点积:离散卷积的特殊情况,即仅向量对应位置分量乘积有定义 |
- 卷积:累计中各点的值变为需累计的值,即二次累计
向量叉积
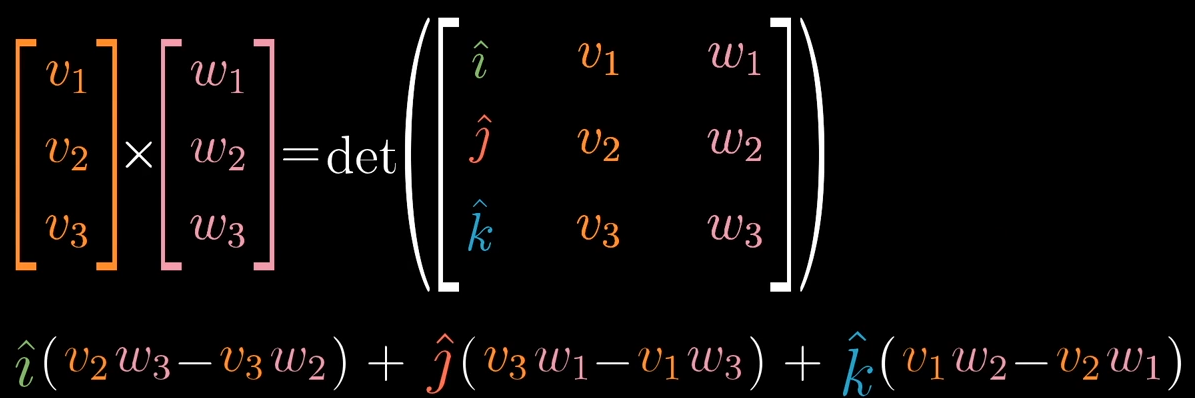
向量叉积意义
向量叉积即寻找向量(到标量的线性变换),满足与其点积结果为张成的体积

考虑点积性质,则向量叉积的方向与向量构成超平面垂直、模为超平面大小

一些规定
正交方向:向量空间 $R^n$ 中 $k, k \leq n$ 个向量 $q^{(1)}, \cdots, q^{(k)}$ 两两正交,则称其为 $k$ 个正交方向,若满足所有向量非 0,则称为 $k$ 个非 0 正交方向
向量左右
- 左侧:向量逆时针旋转 $[0, \pi]$ 内
- 右侧:反左侧
矩阵
矩阵(乘法):对向量的变换
- 对 $m * n$ 矩阵,即将 $n$ 维空间映射至 $m$ 维空间
矩阵相关概念
- (矩阵)秩:空间维数
- (矩阵)零空间/核:变换(左乘矩阵)后落在原点的向量的集合

- 线性变换:保持空间中坐标轴仍为直线且原点保持不变的变换
- 此处若无特殊说明,向量均以列向量作为基础
特殊矩阵
- 其中正交矩阵、三角阵、对角阵也被成为因子矩阵
Orthogonal Matrix 正交矩阵:和其转置乘积为单位阵的方阵
左乘正交矩阵几何意义:等价于旋转
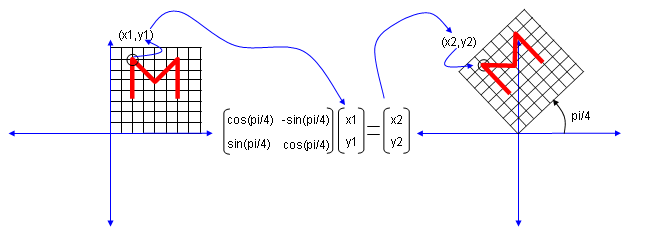
- 酉矩阵/幺正矩阵:$n$ 个列向量是 $U$ 空间标准正交基的 $n$ 阶复方阵,是正交矩阵往复数域上的推广
Diagonal Matrix 对角阵:仅对角线非0的矩阵
左乘对角阵矩阵几何意义:等价于对坐标轴缩放
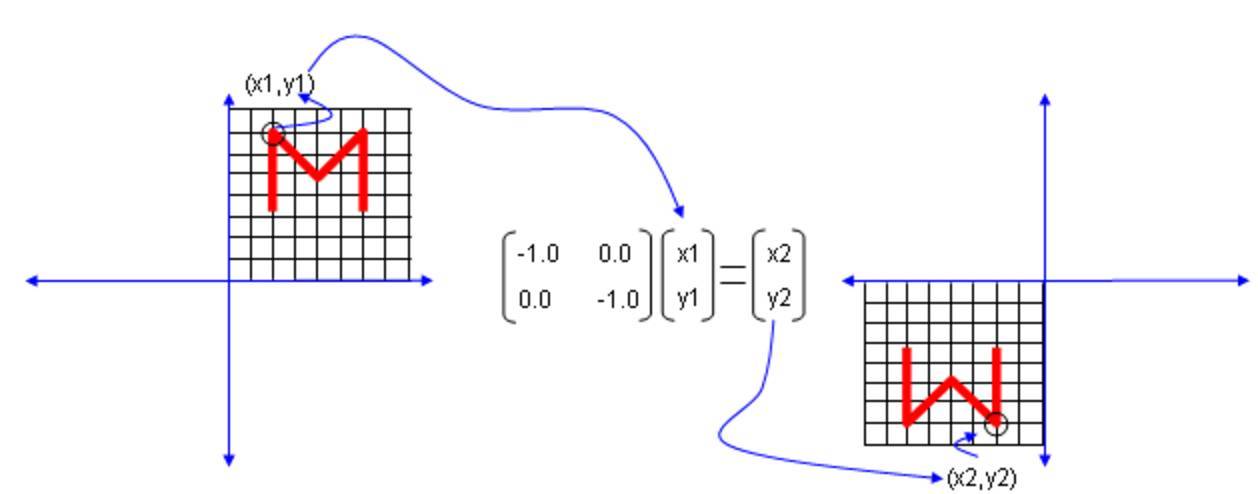
Triangular Matrix 上/下三角矩阵:左下/右上角全为0的方阵
- 三角阵是高斯消元法的中间产物,方便进行化简、逐层迭代求解线性方程组
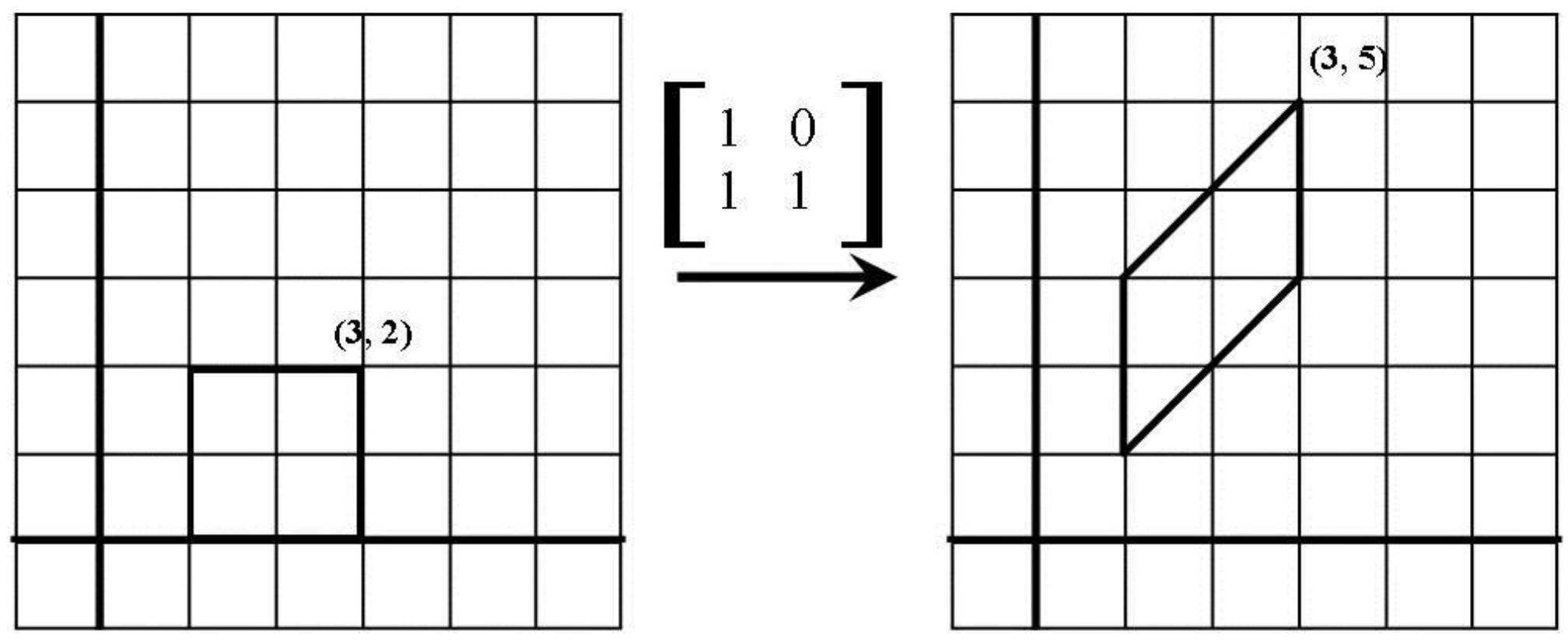
左乘上三角阵几何意义:等价于进行右上切变(水平斜拉)
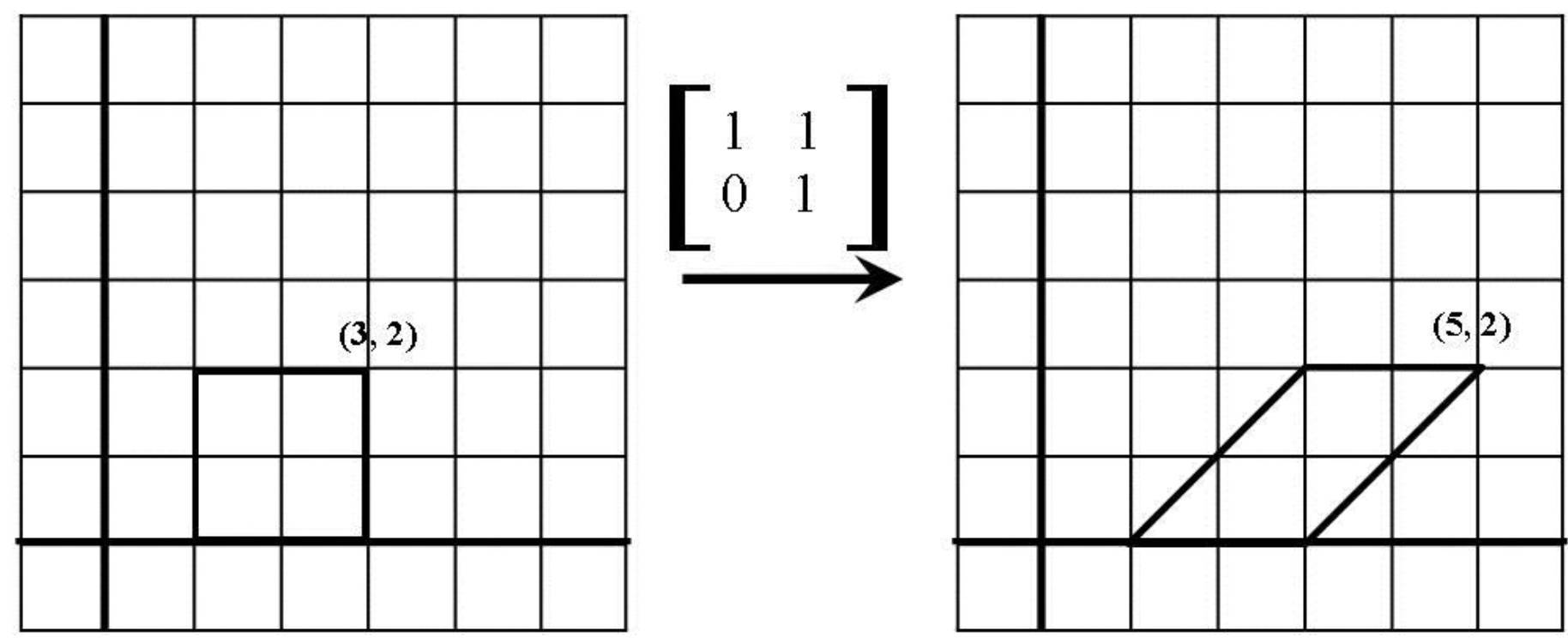
左乘下三角阵几何意义:等价于进行左下切变(竖直斜拉)
Transposation Matrix 置换矩阵:系数只由 0、1 组成,每行、列恰好有一个 1 的方阵
矩阵常用公式
Sherman-Morrison 公式
- 设A是n阶可逆矩阵,$u, v$均为n为向量,若 $1 + v^T A^{-1} u \neq 0$,则扰动后矩阵$A + u v^T$可逆
矩阵乘法
矩阵乘法
向量左乘矩阵:即是对向量进行变换

矩阵乘积:复合变换

- 矩阵乘法应按照从右往左阅读,右侧矩阵为输入、左侧矩阵为变换(向量默认为列向量时)
Affline Transformation
仿射变换:对向量空间进行线性变换、平移得到另一个向量空间

- $y \in R^n, x \in R^n$
- $A \in R^{n * n}$:可视为产生旋转、放缩
- $b \in R^n$:可视为产生平移
仿射变换可以理解为:放缩、旋转、平移
从仿射变换的角度,对向量空间进行仿射变换
- $n+1$ 对变换前、变换后向量坐标即可以求解仿射变换的全部参数
- 变换后的向量之间仍然保留某种相关性,所以 $n+1$ 对向量坐标可以完全确定仿射变换
从仿射变换几何含义,将向量空间中向量统一变换
- $n+1$ 个不共线 $n$ 维向量即唯一确定n维空间
- 若所有向量变换均遵循同一“线性”变换规则,即进行相同放缩、旋转、平移,则这样的变换可以使用仿射变换表示
说明
- $n$ 变换前、变换后向量坐标可以求解 $A$(不考虑 $b$),但第 $n+1$ 对向量坐标未必满足 $A$ 变换
- 若 $n+2$ 对向量坐标不满足 $(A|b)$ 的解,则表示不是进行仿射变换
Perspective Transformation
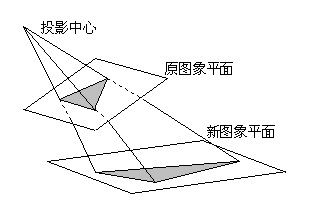
透视变换:将向量空间映射到更高维度,再降维到另一向量空间
- $P \in R^{(n+1) (n+1)}, A \in R^{n n}$
- $x \in R^n, y \in R^{n+1}$:这里默认$x$第$n+1$维为1
- $c$:可视为产生透视,若其为0向量,则退化为仿射变换
- $p_{n+1,n+1}$:可视为决定透视放缩,所以若是已确定新向量空间的“位置”,此参数无效,即 $n+2$ 对向量坐标即可求解变换
透视变换虽然是向量空间变换至另一向量空间,但仍然存在一个透视“灭点”,作为所有透视线的交点
- 对平面成像而言,“灭点”是成像平面、视角决定
变换后 $y$ 维数增加,一般会再次投影、缩放回原维度空间,如原向量空间 $(R^n,1)$
- 仿射变换可以视为是新的向量空间和原始空间“平行”的透视变换特例
变换矩阵求解
- 考虑变换后再次缩放回更低维 $(R^n,1)$ 向量空间
- $\gamma$:变换后向量缩放比例
- 可解性
- 共 $n+2$ 对变换前、后向量坐标,即 $n*(n+2)$ 组方程
- 对每对向量,其中 $n$ 组方程如上可以看出是齐次方程组,不包含常数项
- 则对 $P \in R^{(n+1) * (n+1)}$ 中除 $p_{n+1,n+1}$ 其他项均可被其比例表示(不含常数项)
- 当然 $p_{n+1,n+1}$ 可以置 1 参加运算,不影响结果
Determinant
矩阵行列式几何意义:线性变换对空间的拉伸比例
- 行列式绝对值:拉伸的比例的绝对大小
- 行列式为 0 时则表示空间降维
- 则显然应有 $det(M_1 * M_2) = det(M_1) det(M_2)$
- 行列式正负号:拉伸的方向

- 行列式绝对值:拉伸的比例的绝对大小
矩阵行列式的用途
- 行列式为 0 意味着矩阵表示降维变换,则对应线性方程组仅在方程组右侧在矩阵张成空间内,即扩展矩阵秩不增时有解
特别的
$2 * 2$ 矩阵 $\begin{vmatrix} a & b \ c & d \end{vmatrix} = ad - bc$
- $a, d$ 分别表示 $(1,0)$、$(0,1)$ 正向放缩比例
- 而 $b, c$ 则相应的为逆向放缩比例
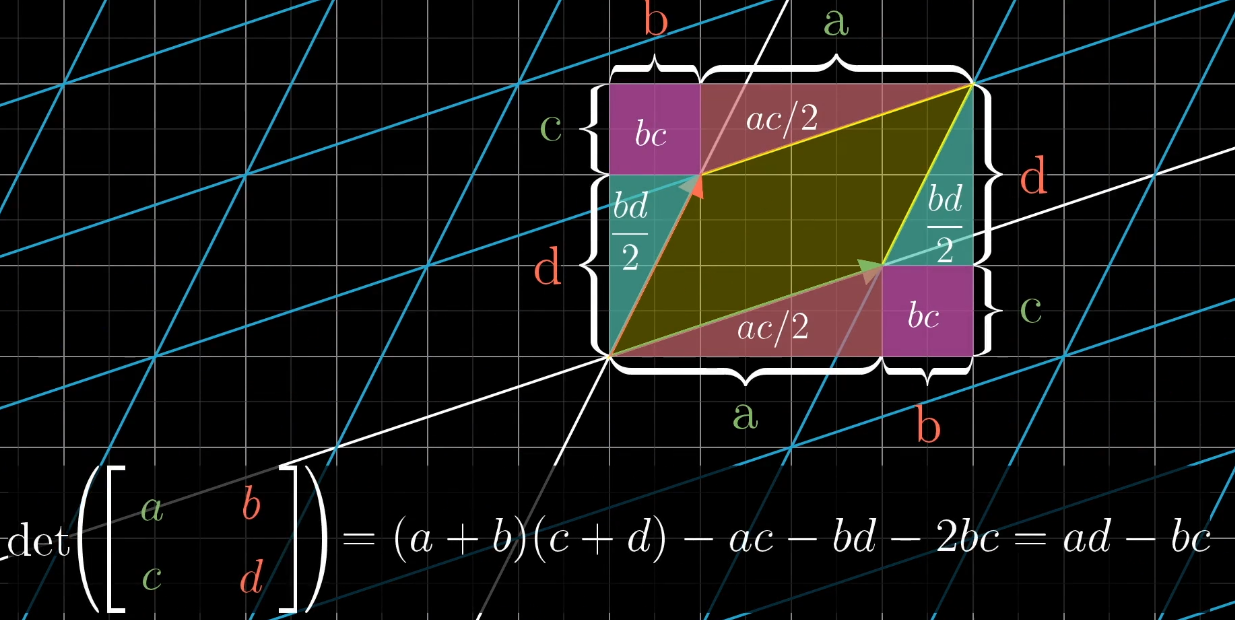
二维三点:行列式绝对值为三点构成三角形面积两倍
- $q_3$ 位于 $\overrightarrow{q_1q_2}$ 左侧:行列式大于0
- $q_3q_1q_2$ 共线:行列式值为 0
三维三点:行列式为三个向量张成的平行六面体体积
Eigen Value、Eigen Vector
矩阵(变换)特征向量、特征值几何意义
- 特征向量:在线性变换后仍然在自身生成空间中,即保持方向不变,仅是模变化的向量
- 特征值:对应特征向量模变化的比例
特殊变换中的特征向量、特征值情况
- 旋转变换:特征值为 $\pm i$,没有特征向量,即特征值为复数表示某种旋转
- 剪切变换($\begin{vmatrix} A^{‘} & 0 \ 0 & 1 \end{vmatrix}$$:必然有特征值为 1,且对应特征向量在坐标轴上
- 伸缩变换($\lambda E$):所有向量都是特征向量
矩阵对角化
- 矩阵对角化:即寻找一组基,使得线性变换对该组基向量仅引起伸缩变换
- 定理:当且仅当 $n$ 阶矩阵 $A$ 有 $n$ 个线性无关的特征向量时,其可以对角化
- 即变换后有 $n$ 个线性无关向量在自身生成空间中
- 也即矩阵对应变换为线性变换
线性方程组
Gaussian Elimination
高斯消元法:初等变换n个线性方程组为等价方程组,新方程组系数矩阵为上三角矩阵
- 三角系数矩阵可以方便的递推求解
- 初等变换可将系数矩阵变换为上三角矩阵,而不影响方程解
