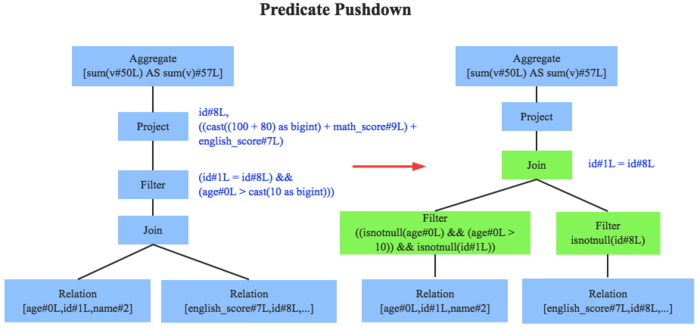
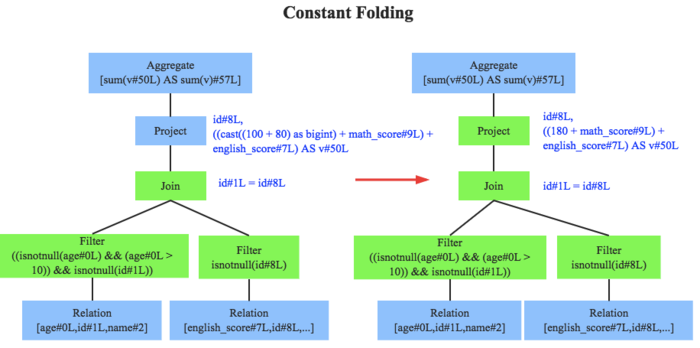
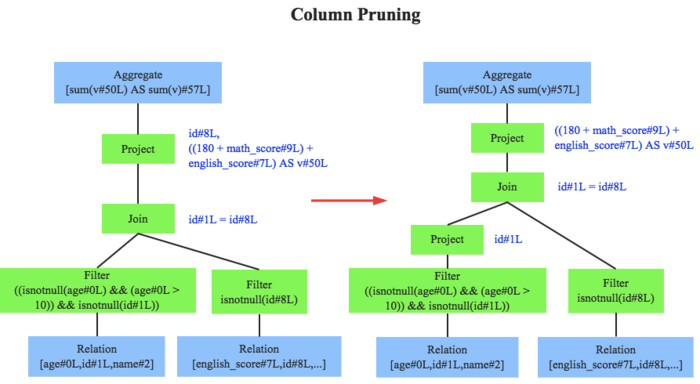
物理查询优化
查询代价估算
代价模型
代价估计模型:基于CPU代价、IO代价
- $P$:计划访问的页面数
- $CPUTimePerPage$:读取每个页面的时间花费
- $T$:访问的元组数,索引扫描应包括索引读取花费
- 反映CPU代价,因为访问页面上的元组需要解析元组结构, 消耗CPU
- $W$:selectivity,选择率/权重因子,表明IO、CPU的相关性
Selectivity
选择率:在关系R中,满足条件A <cond_op> a的元组数R和
所有元组数N的比值
- 在CBO中占有重要地位
- 其精确程度直接影响最优计划的选择
估计方法
Non-Parametric Method:非参方法,使用ad-hoc数据结构、 直方图维护属性值分布
Parametric Method:参数方法,使用预先估计的分布函数 逼近真实分布
Curve Fitting:曲线拟合法,使用多项式函数、最小标准差 逼近属性值分布
Sampling:抽样法,从数据库中抽取部分元组,针对样本进行 查询,收集统计数据
- 需要足够多样本被测试才能达到足够精度
综合法
单表扫描算法
索引
两表联接算法
todo
Nested Loop
嵌套循环联接算法:扫描外表,读取记录根据join字段上的
索引去内表中查询
- 适合场景
- 外表记录较少(<1w)
- 内表已经创建索引、性能较好
- inner、left outer、left semi、left antisemi join
嵌套循环联接算法
- 搜索时扫描整个表、索引
1 | for each row R1 in the outer table: |
- 外部循环逐行消耗外部输入表,当其数据量很大时可以并行扫描 内表
- 内表被外表驱动:内部循环为每个外部行执行,在内表中搜索 匹配行
基于块嵌套循环联接算法
- 每次IO申请以“块”为单位尽量读入多个页面
- 改进获取元组的方式
1 | for each chunk c1 of t1 |
- 内存循环最后一个块使用后作为下次循环循环使用的第一个块 可以节省一次IO
索引嵌套循环联接算法
- 索引嵌套循环连结:在内表中搜索时使用索引,可以加快联接 速度
- 临时索引嵌套循环连结:为查询临时生成索引作为查询计划的 一部分,查询完成后立刻将索引破坏
(Sort)Merge Join
排序归并联接算法
- 适合场景
- 联接字段已经排序,如B+树索引
- inner、left outer、left semi、left anti semi、 right outer、right semi、right anti semi join、union
- 等值、非等值联接,除
!=/<>
算法
确保两个关联表都是按照关联字段进行排序
- 若关联字段已经有排序一致的可用索引,可以利用索引直接 进行merge join操作
- 否则先对关联字段进行排序,表过大无法一次载入内存时 需要分块载入
从每个表分别取记录开始匹配(升序)
Hash Join
哈希联接:利用Hash Match联接
HJ处理代价非常高,是服务器内存、CPU头号杀手,需要对数据 进行分区时,还会造成大量异步磁盘I/O,避免大数据的HJ, 尽量转化为高效的SMJ、NLJ
- 表结构设计:冗余字段
- 索引调整设计
- SQL优化
- 冗余表:静态表存储统计结果
类似任何hash算法,内存小、数据偏斜严重时,散列冲突会比较 严重,此时应该考虑使用NIJ
适合场景
- 两表数据量相差非常大
- 对CPU消耗明显,需要CPU资源充足
- 只适合(不)等值查询
In-Memory Hash Join
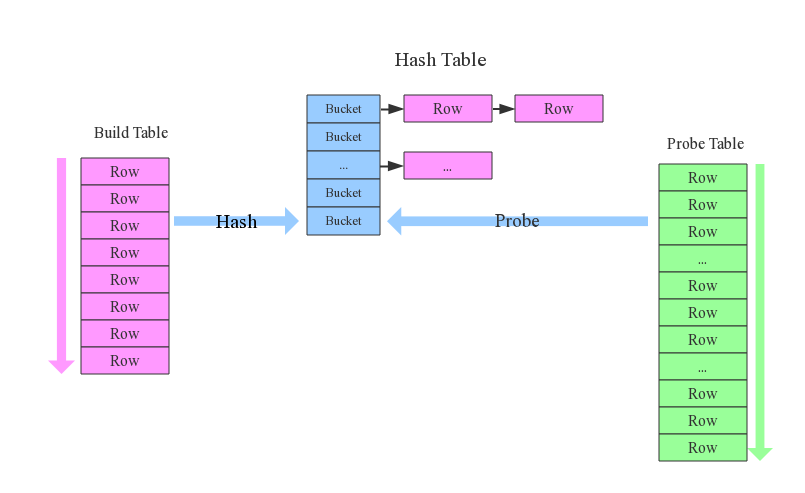
build阶段
以操作涉及字段为hash key构造hash表
从构造输入表中取记录,使用hash函数生成hash值
hash值对应hash表中的buckets,若一个hash值对应多个桶, 则使用链表将联接桶
构造输入表处理完毕之后,其中记录都被桶关联
- build表构建的hash表需要频繁访问,最好能全部加载在内存中 ,因此尽量选择小表,避免使用GHJ
probe阶段
从探测输入中取记录,使用同样hash函数生成hash值
根据hash值,在构造阶段构造的hash表中搜索对应桶
- 为避免冲突,bucket可能会联接到其他bucket,探测操作 会搜索整个冲突链上的buckets查找匹配记录
具体操作
以下操作内部实现其实都是hash join,只是对应算符不同而已
join操作
- 使用join字段计算hash值
- 使用顶端输入构造hash表,底端输入进行探测
- 按照联接类型规定的模式输出(不)匹配项
- 若多个联接使用相同的联接列,这些操作将分组为一个 哈希组
grouby操作、unique操作
- 使用groupby字段、所有select字段计算hash值
- 使用输入构造hash表,删除重复项、计算聚合表达式
- 扫描hash表输出所有项
union操作、需要去除重复记录操作
- 所有select字段计算hash值
- 第一个输入构建hash表,删除重复项
- 第二个输入进行探测
- 若第二个输入没有重复项,直接返回没有匹配的项, 扫描hash表返回所有项
- 若第二个输入有重复项,则应该需要继续构建hash表, 最后统一输出整个hash表
Grace Hash Join
grace hash join:磁盘分块HJ
将两表按照相同hash函数分配至不同分片中
- 在磁盘上为各分片、表建立相应文件
- 对表输入计算哈希值,根据哈希值写入分片、表对应文件
再对不同分片进行普通in-memory hash join
- 若分片依然不能全部加载至内存,可以继续使用 grace hash join
1 | grace_hash_join(t1, t2): |
分片数量
PART_COUNT决定磁盘IO效率- 分片数量过小:无法起到分治效果,分片仍然需要进行 grace hash join,降低效率
- 分片数量过大:磁盘是块设备,每次刷盘刷一定数量块才 高效,频繁刷盘不经济
- 即分片数量在保证刷盘经济的情况下,越大越好,这需要 优化器根据表统计信息确定
特点
- 有磁盘I/O代价,会降低效率
- 适合参与join表非常大,无法同时载入内存中
Hybrid Hash Join
hybrid hash join:GHJ基础上结合IMHJ的改进
- 对build表分片过程中,尽量多把完整分片保留在内存中
- 对probe表分片时,对应分片可以直接进行probe操作
- hybrid hash join有时也被直接视为grace hash join, 不做区分
比较
资源消耗
- HJ:CPU计算、内存(磁盘)中创建临时hash表
- SMJ:磁盘I/O(扫描表、索引)
- NLJ:磁盘I/O
性能
通常情况:HJ > NPJ <> SMJ
- 全表扫描比索引范围扫描再进行表访问更可取时,SMJ 优于NPJ???
- 而表特别小、特别大时,全表扫描优于索引范围扫描
但若关联字段已排序,SMJ性能最优
首条搜索结果
- NPJ能快速返回首条搜索结果
- HJ、SMJ返回首条结果较慢
多表联接算法
多表联接算法:找到最优连接顺序(执行路径)
表联接顺序对于查询结果没有影响,但是对资源消耗、性能影响 巨大
随着需要联接表数目增加,可能的联接排列非常多,基本不能 对所有可能穷举分析
- left-deep tree/linear (processing)tree:$n!$
- bushy tree:$\frac {2(n-1)!} {(n-1)!}$ (包括left-deep tree、right-deep tree)
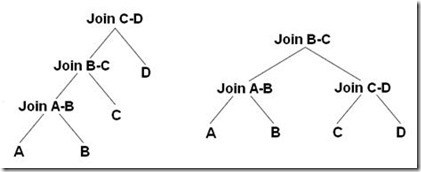
事实上查询优化器不会穷尽搜索所有可能联接排列,而是使用 启发式算法进行搜索
Dynamic Programming
动态规划算法:依次求解各数量表最优联接顺序,直到求出最终结果
构造第一层关系:每个关系的最优路径就是关系的最优单表扫描 方式
迭代依次构造之后n-1层关系联接最优解
- 左深联接树方式:将第k-1层每个关系同第1层关系联接
- 紧密树联接方式:将第m(m > 2)层每个关系同第k-m层关系 联接

Heuristic Algorithm
Greedy Algorithm
贪心算法:认为每次连接表的连接方式都是最优的,即从未联接表中 选择使得下次联接代价最小者
多表排序一般为
- 常量表最前
- 其他表按可访问元组数量升序排序
贪心算法得到的联接方式都是最优的
- 则每次联接主要求解要联接表对象的最佳访问方式
- 即每次代价估计的重点在于单表扫描的代价
求解结束后,局部最优查询计划生成
- 得到左深树
- 最初始表位于最左下端叶子节点处
System R
System R:对动态规划算法的改进
- 保留子树查询最优、次优查询计划,用于上层查询计划生成, 使得查询计划整体较优
Genetic Algorithm
遗传算法:模拟自然界生物进化过程,采用人工进化的方式对目标 空间进行搜索
- 本质是高效、并行、全局搜索方法
- 能在搜索过程中自动获取、积累有关搜索空间的知识,并自适应 的控制搜索过程以求的最佳解
思想
- 将问题域中可能解看作是染色体,将其编码为符号串的形式
- 对染色体群体反复进行基于遗传学的操作:选择、交叉、变异
- 根据预定目标适应度函数对每个个体进行评价,不断得到更优 群体,从中全局并行搜索得到优化群体中最优个体
实体
- population:群体,GA的遗传搜索空间
- individual:个体,搜索空间中可能解
- chromosome:染色体,个体特征代表
- 由若干段基因组成
- GA中基本操作对象
- gene:基因
- 染色体片段
- fitness:适应度,个体对环境的适应程度
基本操作
selection:选择,根据个体适应度在群体中按照一定概率 选择个体作为父本
- 适应度大个体被选择概率高
- 体现了适者生存、优胜劣汰的进化规则
crossover:交叉,将父本个体按照一定概率随机交换基因 形成新个体
mutate:变异,按照一定概率随机改变某个体基因值
涉及问题
串编码方式
- 把问题的各种参数用二进串进行编码构成子串
- 把子串拼接成染色体
- 串长度、编码方式对算法收敛影响极大
适应度/对象函数确定
- 一般可以把问题模型函数作为对象函数
GA超参设置
- 群体大小$n$:过小难以求出最优解,过大难收敛,一般取 $n = 30 ~ 160$
- 交叉概率$P_c$:太小难以前向搜索,太大容易破坏高适应 值结构,一般取$P_c = 0.25 ~ 0.75$
- 变异概率$P_m$:太小难以产生新结构,太大则变为单纯 随机搜索,一般取$P_m = 0.01 ~ 0.2$
算法
- 随机初始化种群
- 估初始种群:为种群每个个体计算适应值、排序
- 若没有达到预定演化数,则继续,否则结束算法
- 选择父体
- 杂交:得到新个体
- 变异:对新个体变异
- 计算新个体适应值,把适应值排名插入种群,淘汰最后个体
- 重复3