传统图像特征提取
Scale-Invariant Feature Transform
SIFT:通过求图中interest/corner point、及其scale和 orientation描述子得到特征,并进行图像特征点匹配
- SIFT是检测局部特征的算法
- 实质:在不同尺度空间查找关键点,计算关键点大小、方向 、尺度信息,进而组成对关键点得描述
- SIFT查找的关键点为突出、稳定的特征点,不会因光照、
仿射变换、噪声等因素而改变
- 角点
- 边缘点
- 暗区亮点
- 亮区暗点
- 匹配过程就是对比特征点过程
优点
- 稳定性:具有旋转、尺度、平移、视角、亮度不变性, 利于对目标特征信息进行有效表达
- 独特性:信息量丰富,适合海量特征数据中进行匹配
- 多量性:少数物体也可以产生大量SIFT特征向量
- 可扩展性:可以方便同其它形式特征向量联合
- 对参数调整稳健性好:可以根据场景调整特征点数量进行 特征描述、方便特征分析
缺点
- 不借助硬件加速、专门图像处理器难以实现
构建尺度空间
图像的尺度空间:解决如何对图像在所有尺度下描述的问题
思想:对原始图像进行尺度变换,获得多尺度空间下图像表示 序列,模拟图像数据的多尺度特征
- 对序列进行尺度空间主轮的提取
- 以主轮廓作为特征向量,实现边缘、角点检测、不同分辨率 上稳定关键点提取
对高斯金字塔生成的O组、L层不同尺度图像,$(O, L)$就构成 高斯金字塔的尺度空间
- 即以高斯金字塔组$O$、层$L$作为坐标
- 给定一对$(o,l)$即可唯一确定一幅图像
图像金字塔
图像金字塔:以多分辨率解释图像的结构
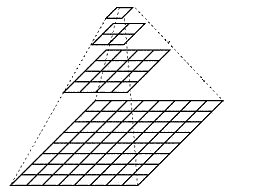
通过对原始图像进行多尺度像素采样方式生成N个不同 分辨率的图像
- 图像分辨率从下至上逐渐减小
- 直至金字塔顶部只包含一个像素
获取图像金字塔步骤
- 利用低通滤波器平滑图像
- 对平滑图像进行采样
- 上采样:分辨率逐渐升高
- 下采样:分辨率逐渐降低
高斯金字塔
高斯金字塔:由很多组图像金字塔构成,每组金字塔包含若干层
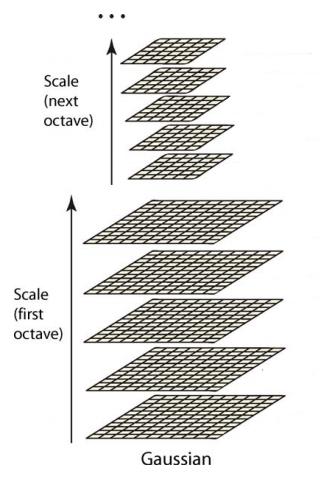
同一组金字塔中
- 每层图像尺寸相同
- 仅高斯平滑系数$\sigma$不同,后一层图像是前一层$k$倍
不同组金字塔中
- 后一组图像第一个图像是前一组倒数第三个图像二分之一 采样
- 图像大小是前一组一半
构建过程
构建第1组图像金字塔
第1层:将原图扩大一倍得到
第2层:第1层图像经过高斯卷积得到
- SIFT算子中,高斯平滑参数$\sigma=1.6$
第k层:
- $\sigma$乘以比例系数得到新平滑因子 $\sigma = k\sigma$,
- 使用平滑因子平滑第k层图像得到
不断重复得到L层图像
构建第k组图像金字塔
第1层:将第k-1组金字塔倒数第3层做比例因子为2的降采样 得到
之后同第1组图像金字塔
不断重复得到O组图像金字塔,共计O * L个图像
Difference of Gaussian
DOG金字塔:差分金字塔
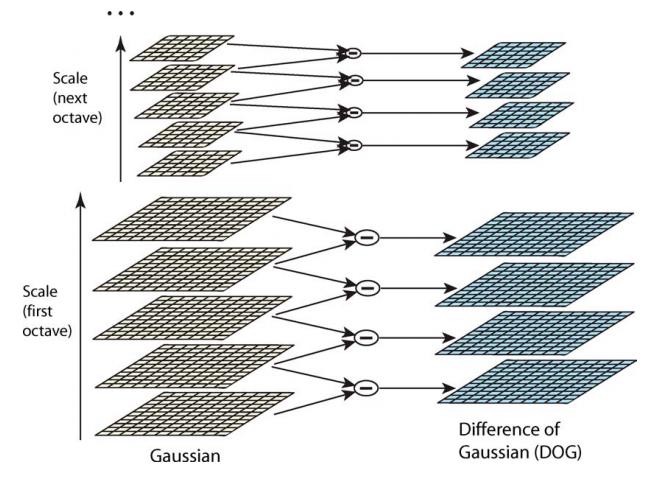
DOG金字塔第0组第k层由高斯金字塔第0组第k+1层减去第k层得到
- DOG金字塔每组比高斯金字塔少一层
- 按高斯金字塔逐组生成$O * (L-1)$个差分图像
DOG图像包含大量信息(需要归一化才能人眼可见)
- 在不同DOG层(即不同模糊程度、不同尺度)都存在的特征 即SIFT要提取的稳定特征
- 后续SIFT特征点都是在DOG金字塔中进行
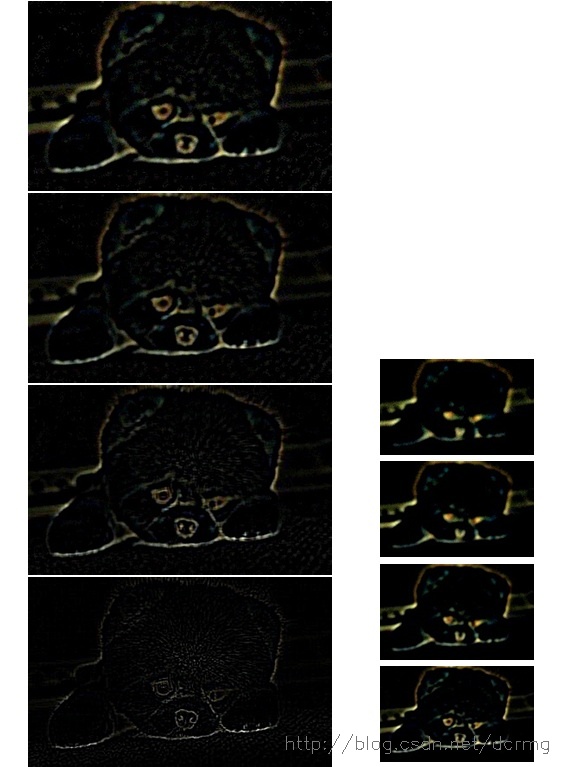
空间极值点检测
空间极值点检测:关键点初步查探
寻找DOG图像极值点:每个像素点和其所有相邻点比较
- 需要同时比较图像域、尺度空间域相邻点
- 保证关键点在尺度空间、二维图像空间上都是局部极值点
对二维图像空间,对中心点
- 图像域:与3 * 3领域内8个点比较
- 同组尺度空间:和上下两层图像中2 * 9个点比较
极值点是在不同尺度空间下提取的,保证了关键点尺度不变性
精确定位
稳定关键点精确定位
DOG值对噪声、边缘敏感,需要对局部极值进一步筛选,去除 不稳定、错误检测极值点
构建高斯金字塔时采用下采样图像,需要求出下采样图像中 极值点对应在原始图像中确切位置
方向信息分配
稳定关键点方向信息分配
为关键点分配方向信息赋予关键点旋转不变性
通过对稳定关键点求梯度实现方向分配
计算方式
梯度幅度值
梯度方向
通过梯度方向直方图给出关键点梯度方向
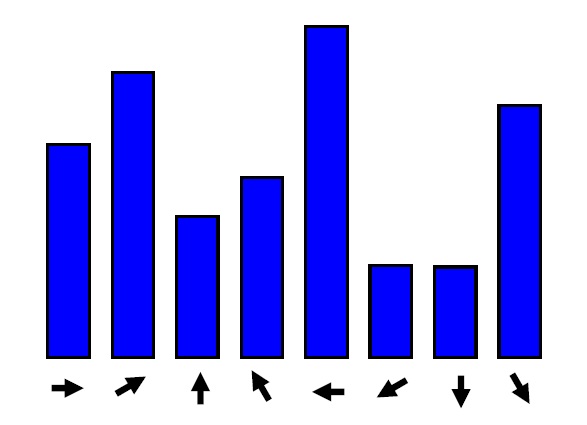
- 计算关键点为中心领域内所有点梯度方向,在0~360度范围
- 把所有梯度方向划分到36个区域,每个方向代表10度
- 累计每个方向关键点数目,生成梯度方向直方图
- 将直方图中峰值代表方向作为关键点主方向
若存在相当于峰值80%大小的方向,则作为辅方向
- 辅方向可以增强匹配的鲁棒性
- Lowe指出:大概15%关键点具有辅方向,且这些关键点 对稳定匹配起关键作用
关键点描述
关键点描述:以数学方式定义关键点的过程,包括关键点周围对其 有贡献的领域点
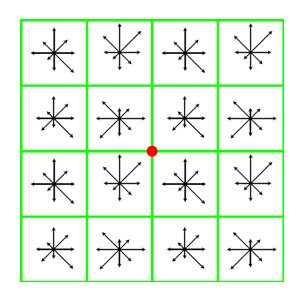
对关键点周围像素区域分块
- 计算块内梯度直方图
- 生成具有独特性的向量,作为对该区域图像信息的抽象表述
如下图
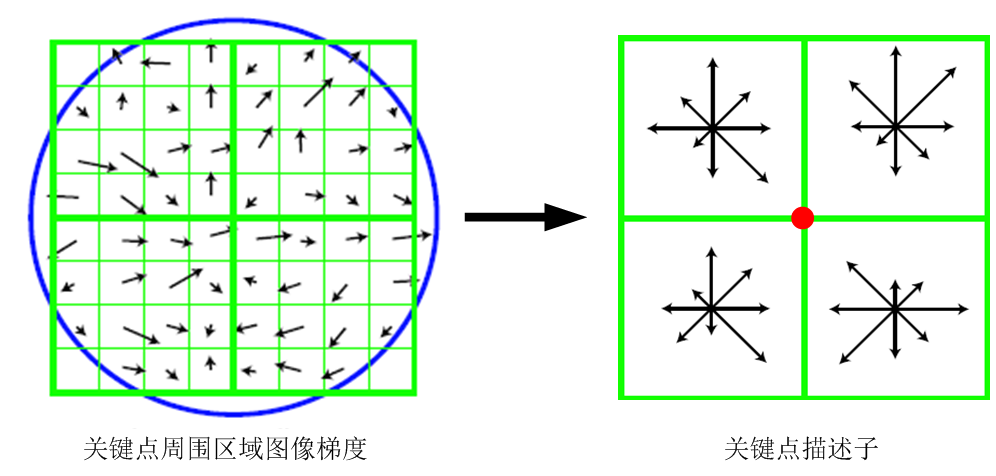
- 将关键点周围分为2 * 2块
- 对每块所有像素点梯度做高斯加权(softmax拉开差距?)
- 每块最终取8个方向,得到2 2 8维向量,作为中心 关键点数学描述
- Lowe实验表明:采用4 4 8共128维描述子表征关键点, 综合效果最好
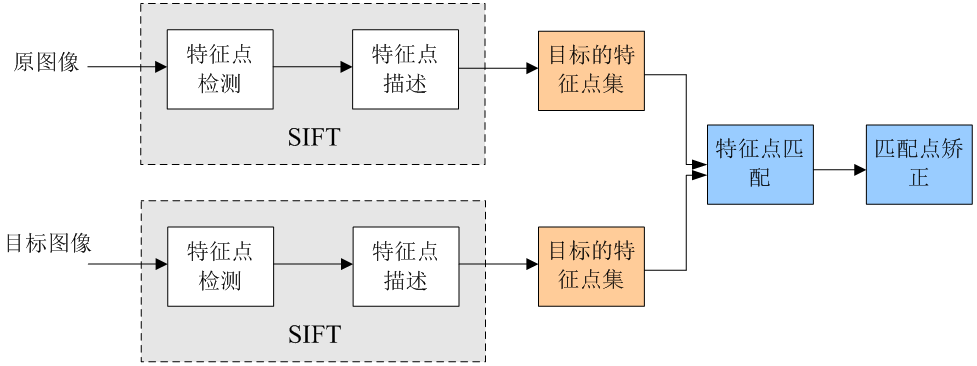
特征点匹配
特征点匹配:计算两组特征点128维描述向量的欧式距离
- 欧式距离越小、相似度越高,小于指定阈值时既可认为匹配成功
Speeded Up Robust Feature
SURF特征:对SIFT算法的改进,降低了时间复杂度,提高了稳健性
- 主要是简化SIFT一些运算
- 高斯二阶维分模型简化,卷积平滑操作仅需要转换为加减 运算
- 最终生成特征向量维度从128维减少为64维
Brief
Oriented Brief
ORB:Brief算法改进版
- 比SIFT算法快100倍