特征编码
数值化:分类->数值
Ordinal Encoding
序号编码:使用一位序号编码类别
- 一般用于处理类别间具有大小关系的数据
- 编码后依然保留了大小关系
One-hot Encoding
独热编码:采用N位状态位对N个可能取值进行编码
一般用于处理类别间不具有大小关系的特征
独热编码后特征表达能力变差,特征的预测能力被人为拆分为多份
- 通常只有部分维度是对分类、预测有帮助,需要借助特征选择降低维度
- 在经典统计中,为避免完全多重共线性,状态位/哑变量会比取值数量少 1
优点
- 能处理非数值属性
- 一定程度上扩充了特征
- 编码后向量时稀疏向量:可以使用向量的稀疏存储节省空间
- 能够处理缺失值:高维映射方法中增加维度表示缺失
缺点
k-NN 算法:高维空间两点间距离难以有效衡量
逻辑回归模型:参数数量随维度增加而增大,增加模型复杂度,容易出现过拟合
决策树模型
- 产生样本切分不平衡问题,切分增益非常小
- 每个特征只有少量样本是 1,大量样本是 0
- 较小的拆分样本集占总体比例太小,增益乘以所占比例之后几乎可以忽略
- 较大拆分样本集的几乎就是原始样本集,增益几乎为 0
- 影响决策树的学习
- 决策树依赖数据统计信息,独热编码将数据切分到零散小空间上,统计信息不准确、学习效果差
- 独热编码后特征表达能力边人为拆分,与其他特征竞争最优划分点失败,最终特征重要性会比实际值低
- 产生样本切分不平衡问题,切分增益非常小
Binary Encoding
二进制编码:先用序号编码给每个类别赋予类别 ID,然后将类别 ID 对应二进制编码作为结果
- 本质上利用二进制类别 ID 进行哈希映射,得到 0/1 特征向量
- 特征维度小于独热编码,更节省存储空间
Weight of Evidence Encoding
WOE 编码:以分类变量各取值的 WOE 值作为编码值
- $\%B_i, \%G_i$:分类变量取第 $i$ 值时,预测变量为 B 类、G 类占所有 B 类、G 类比例
- $#B_i, #B_T$:分类变量取第 $i$ 值时,预测变量为 B 类占所有 B 类样本比例
- $#G_i, #G_T$:分类变量取第 $i$ 值时,预测变量为 G 类占所有 G 类样本比例
WOE 编码是有监督的编码方式,可以衡量分类变量各取值中
- B 类占所有 B 类样本比例、G 类占所有 G 类样本比例的差异
- B 类、G 类比例,与所有样本中 B 类、G 类比例的差异
WOE 编码值能体现分类变量取值的预测能力,变量各取值 WOE 值方差越大,变量预测能力越强
- WOE 越大,表明该取值对应的取 B 类可能性越大
- WOE 越小,表明该取值对应的取 G 类可能性越大
- WOE 接近 0,表明该取值预测能力弱,对应取 B 类、G 类可能性相近
优势
相较于 one-hot 编码
- 特征数量不会增加,同时避免特征过于稀疏、维度灾难
- 避免特征筛选过程中,一部分特征取值被筛选,一部分被遗弃,造成特征不完整
- 将特征规范到同一尺度的数值变量,同时也便于分析特征间相关性
在 LR 模型中,WOE 编码线性化赋予模型良好的解释性
- WOE 编码本身即可反应特征各取值贡献
- 可以用于给评分卡模型中各分箱评分
分类化/离散化:数值->分类
- 分类型变量本质上无法建模,因为取值从含义上无法进行数值计算
- 将数值型映射为分类型,往往只是中间步骤,最终会将分类型取值映射回数值型
- 若分箱数量为 2,也被成为是二元化/布尔化
离散化综述
模型使用离散特征、连续特征,是“海量离散特征+简单模型”、“少量连续特征+复杂模型”的权衡
- 海量离散特征+简单模型:难点在于特征工程,成功经验可以推广,可以多人并行研究
- 少量连续特征+复杂模型:难点在于模型调优,不需要复杂的特征工程
一般的,连续特征对预测结果影响不会突变,合理的离散化不应造成大量信息丢失
- 且若特征存在突变,模型将难以拟合(线性模型尤其)
- 反而更应该离散化为多个分类特征,方便引入非线性
事实上,根据Cover定理,离散化增加特征维度类似于投影至高维,更可能得到较优模型(也更容易过拟合)
- 极限角度,对所有特征、取值均离散化,则可以得到完全可分模型(除特征完全一样分类不同)
描述角度
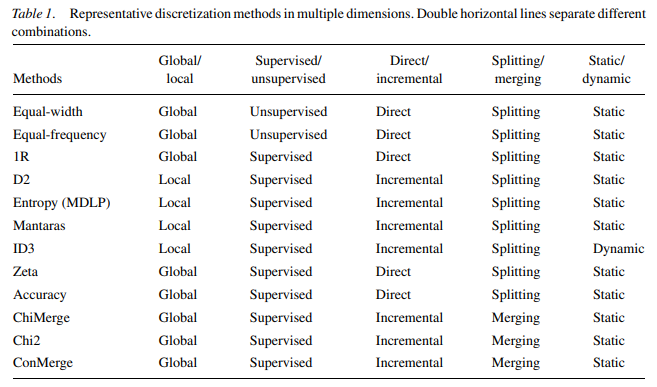
supervised vs. unsupervised:是否使用分类信息指导离散化过程
- 无监督
- 如:等距、等频划分
- 无法较好的处理异常值、不均匀分布
- 有监督
- 利用分类信息寻找合适切分点、间隔
- 根据使用分类信息的方式有许多种
- 无监督
dynamic vs. static:离散化、分类是否同时进行
global vs. local:在特征空间的局部还是全局进行离散化
spliting vs. merging/top-down vs. bottom-up:自顶向下划分还是自底向上合并
direct vs. incremental:直接根据超参数确定分箱数量还是逐步改善直到中止准则
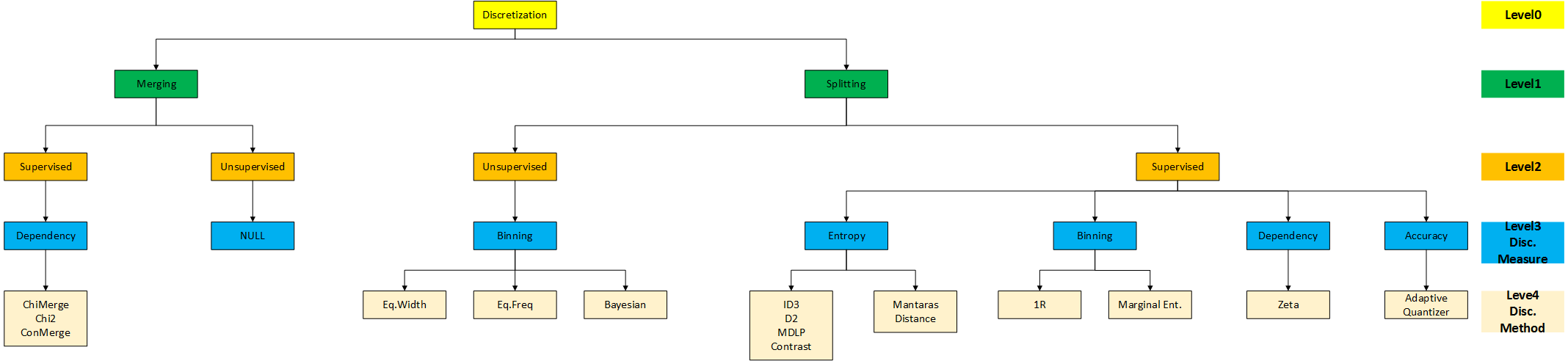
典型过程
- sort:排序
- evaluate:评估分割点
- split or merge:划分、合并
- stop:停止离散化
评价
- Simplicity:可用切分点数量衡量简单性
- Consistency:可以通过最小不一致数量衡量一致性
- 不一致:样本具有相同的特征取值,但分类不同
- 分箱最小不一致数量则为,箱内样本数量减最大类别数量
- Accuracy:可通过分类器进行交叉验证的准确率衡量
优势
方便工业应用、实现
- 离散特征的增加、减少容易,方便模型迭代
- 特征离散化处理缺失值、异常值更方便,可直接将其映射为某取值
- 数值化后可指定取值类型,如:one-hot编码为为稀疏向量
- 內积速度快
- 存储方便
- 容易扩展
方便引入历史经验
- 可以自由调整离散化结果,结合机器学习和历史经验得到最终的离散化结果
模型更稳健
- 模型不再拟合特征具体值,而是拟合某个概念,能够对抗数据扰动,更稳健
- 对异常数据鲁棒性更好,降低模型过拟合风险
- 某些场合需要拟合参数值更少,降低模型复杂度
(引入)非线性提升模型表达能力
- 利用经验、其他信息将数值特征分段,相当于引入非线性,提升线性模型表达能力
- 方便引入交叉特征,提升模型表达能力
适合场景
离散化特征更适合 LR 等线性模型
- 如下离散化优势:方便引入非线性等
- 模型中所有特征都会被考虑,考虑细节、个体(包括 $L_1$ 范数也是被考虑后剔除)
GBDT 等树、抽样模型则不适合
- 特征离散化后,由于抽样误差的存在,可能存在某些离散特征对样本预测能力非常强,非线性模型容易给这些特征更大权重,造成过拟合
- 如:刚好抽取的 1000 个样本中某离散特征取值为 1 者全为正样本
- 树模型每次使用一个特征划分节点,特征数量较多不利于模型训练
- 若单个离散化特征预测能力不强,由于树深度限制,只有少量特征被作为划分依据,模型可能不收敛、表达能力更差
- 若单个离散化特征预测能力强,连续特征也应该也有较好效果
- 特征离散化后,由于抽样误差的存在,可能存在某些离散特征对样本预测能力非常强,非线性模型容易给这些特征更大权重,造成过拟合
无监督
- 无监督分箱仅仅考虑特征自身数据结构,没有考虑特征与目标之间的关系
等频/等距/经验分箱
分箱逻辑
- 等频分箱:排序后按数量等分
- 避免离散化后特征仍然为长尾分布、大量特征集中在少量组内
- 对数据区分能力弱
- 等距分箱:取值范围等分
- 经验分箱
- 等频分箱:排序后按数量等分
分箱数量、边界超参需要人工指定
- 根据业务领域经验指定
- 根据模型指定:根据具体任务训练分箱之后的数据集,通过超参数搜索确定最优分桶数量、边界
分箱经验、准则
- 若组距过大,组内属性取值差距过大
- 逻辑上分类不能够代表组内全部样本,组内取值影响可能完全不同
- 若组距过小,组内样本过少
- 随机性太强,不具备统计意义上说服力
- 特征影响跳变过多
- 若组距过大,组内属性取值差距过大
聚类分箱
- K-Means 聚类
- 层次聚类
- 聚类过程中需要保证分箱有序
有监督
Binning:1R 分箱
- 分箱逻辑、步骤
- 将样本排序,从当前位置开始
- 初始化:以允许的最少样本作为一箱,将箱内最多类别作为箱标签
- 扩展:若下个样本类别与箱标签相同,则划至箱内
- 重复以上,得到多个分箱
- 将相邻具有相同标签的箱合并,得到最终分箱结果
- 将样本排序,从当前位置开始
Splitting
- 基于信息熵的 split,具体划分依据如下
- ID3:信息增益
- C4.5:信息增益比
- D2:
- Minimum Description Length Principle:描述长度
Merge分箱
- 基于依赖相关的 merge,具体划分依据如下
- Chimerge:使用卡方值衡量两个相邻区间是否具有类似分布,若具有类似分布则将其合并
具体算法
- 输入:目标分箱数量 $N$
- 初始化
- 将变量升序排列
- 为减少计算量,若初始分箱数量大于阈值 $N_{max}$,则利用等频分箱进行粗分箱
- 缺失值单独作为一个分箱
- 合并区间
- 计算每对相邻区间的卡方值
- 将卡方值最小区间合并
- 重复以上直至分箱数量不大于 $N$
- 分箱后处理
- 合并纯度为 1(只含有某类样本)的分箱
- 删除某类样本占比超过 95% 的分箱
- 若缺失值分箱各类样本占比同非缺失值分箱,则合并