频繁项集/序列
频繁项集
- 频繁项集:频繁出现项集合(无序)
- 频繁项序列:频繁出现项序列(有序)
- 相关关联规则算法:数据量大时,无法直接发现频繁项集
- 频繁项集评估标准
评估标准
支持度:数据关联出现概率,关联数据在数据集中出现次数占 总数据集比重
- 支持度高数据不一定构成频繁项集,但支持度数据肯定不能 不构成频繁项集
置信度:数据出现条件概率,某个数据出现、另一数据出现概率
提升度:数据之间关联关系,某数据出现、另一数据出现概率同 其总体出现概率之比
- 提升度大于1则为有效的强关联规则,否则为无效的强关联 规则
- 若X、Y不相关,则提升度为1
- 选择频繁数据集,一般需要自定义评估标准:自定义支持度、 自定义支持度和置信度组合
Apriori
Apriori算法
- 以支持度作为评估标准,找出数据集中最大的频繁$k$项集
- 找到符合支持度标准的频繁$k$项集
- 迭代直到无法找到项数更大的频繁项集
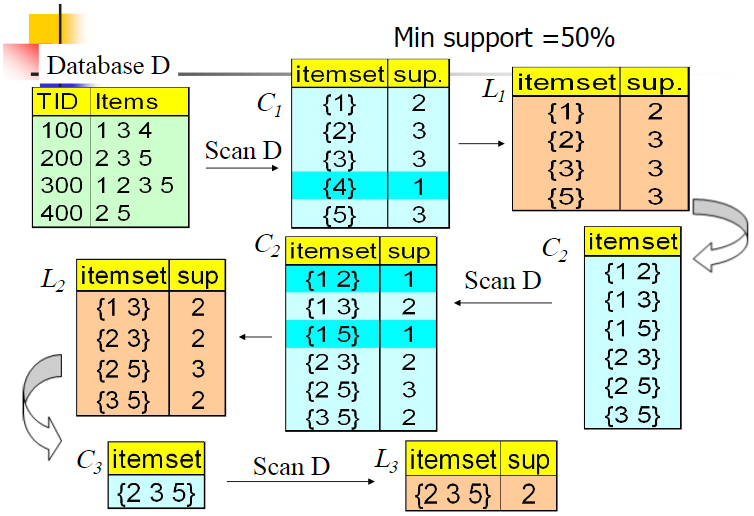
算法
- 输入:数据集合D、支持度阈值$\alpha$
- 输出:最大的频繁K项集
- 置$k=1$,扫描整个数据集,以所有出现过数据作为候选1项集
- 挖掘候选$k$项集
- 扫描数据、计算候选$k$项集支持度
- 去除支持度低于阈值$\alpha$的项集得到频繁$k$项集
- 若频繁$k$项集只包含1项,直接返回
- 若频繁$k$项集为空,返回频繁$k-1$项集
- 基于频繁$k$项集连接、生成候选$k+1$项集
- 置$k=k+1$
- 需要频繁扫描数据、效率低
- 频繁项集的子项集肯定也是频繁项集
FPTree/FPGrowth
FPTree:对Apriori算法改进,不在需要多次扫描数据
FPTree引入部分数据结构以临时存储数据
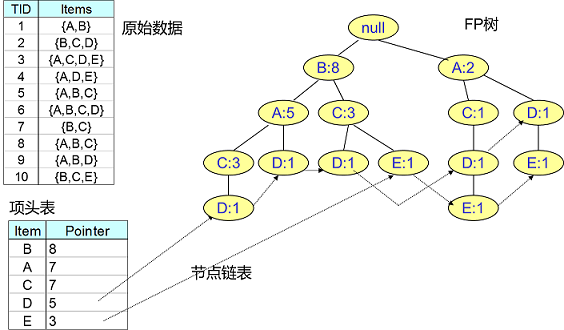
- 项头表:按频繁1项集出现频数降序排列的表
- FP Tree:包含原始数据、频数的多叉树
- 节点链表:链接项头表中频繁1项集、FPTree中相应节点 的链表
特点:效率高
- 只需要扫描两次数据
- 使用多叉树存储临时数据,利用高频频繁项集
算法
建立项头表
- 扫描数据,得到所有1项集频数、剔除支持度低于阈值者, 并按支持度(频数)降序排列
- 第二次扫描数据,剔除每条数据中非频繁1项集、 在每条数据内部按支持度降序排列
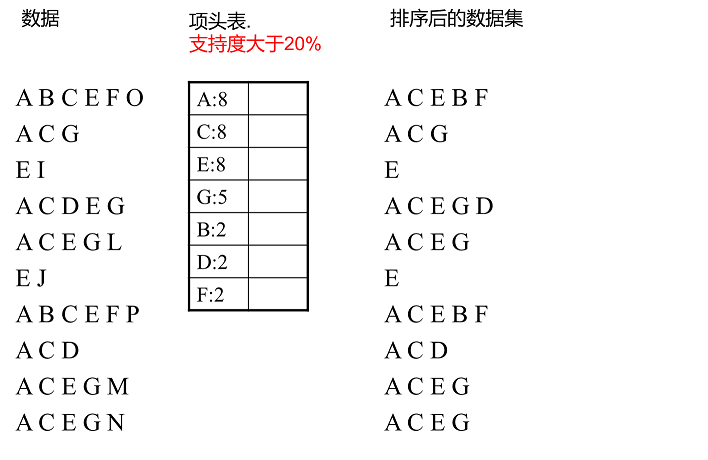
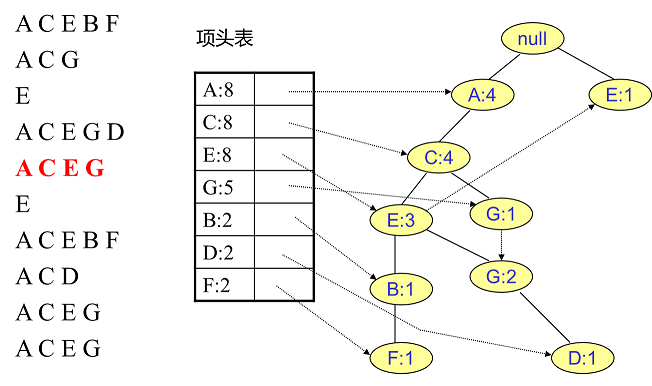
建立FPTree:逐条读取处理后排序后数据,依次插入树中
- 每条数据中排序靠前者为祖先节点
- 若有直系公共祖先则公共祖先节点计数+1
- 新节点通过链表和项头表链接
挖掘FPTree:对项表头中每项,找到其条件模式基
- 将子树中每个节点计数置为叶子节点计数和,则子树中节点 取值即为其与当前项组合出现频数/支持度
- 删除(当前子树内)支持度/频数低于支持度阈值$\alpha$ 节点
- 剩余节点项、当前项组合即为相应频繁$k$项集
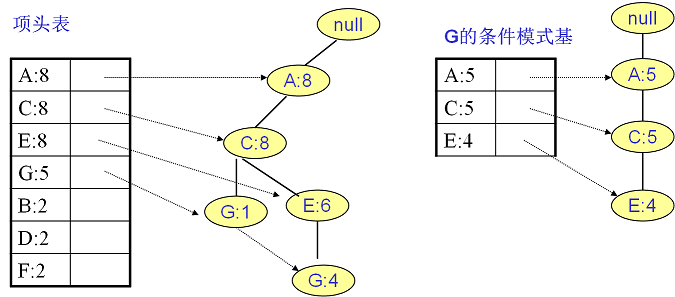
- 条件模式基:节点作为叶子节点所对应的FP子树
Prefix-Projected Pattern Growth
PrefixSpan:前缀投影模式挖掘
- 以支持度为标准,挖掘数据集中频繁序列
- 每条数据为若干项集组成的序列,序列内项集间有序
- 为方便,每条数据序列中项集中的项已排序
- 可以将每条数据序列整体视为串
- 频繁序列:频繁出现子序列
算法
- 输入:序列数据集$S$、支持度$\alpha$
- 所有满足阈值要求的频繁序列
找出所有长度1前缀(即所有项)、对应投影
- 计数、剔除持度小于阈值$\alpha$者,得到频繁1项序列
- 置$k=1$
对每个长度为$k$前缀递归挖掘
- 若前缀对应投影为空,返回
- 若前缀对应投影中所有项支持度均小于阈值$\alpha$,返回
- 同满足阈值要求阈值$\alpha$要求项合并,得到新前缀
- 置$k=k+1$
- prefix:前缀,正在处理的子序列
- projected:投影,各数据序列中位于前缀之后子串 ?串