• Hadoop（核心）：HDFS和MapReduce/YARN
• Hadoop家族：建立在Hadoop基础上的一系列开源工具

Hadoop

Hadoop时Apache的一个分布式计算、java语言实现的开源框架， 实现在大量计算机组成的集群中对海量数据进行分布式计算。相比于 依赖硬件的可靠性，Hadoop被设计为可以检测、处理应用层面的 failures，能够提供构建于电脑集群上的可靠服务。

Hadoop：Apache的分布式计算开源框架，提供分布式文件系统 HDFS、MapReduce/YARN分布式计算的软件架构

Hadoop Common

支持其它Hadoop模块的公用组件

Hadoop Distributed File System(HDFS)

虚拟文件系统，让整个系统表面上看起来是一个空间，实际上是很多 服务器的磁盘构成的

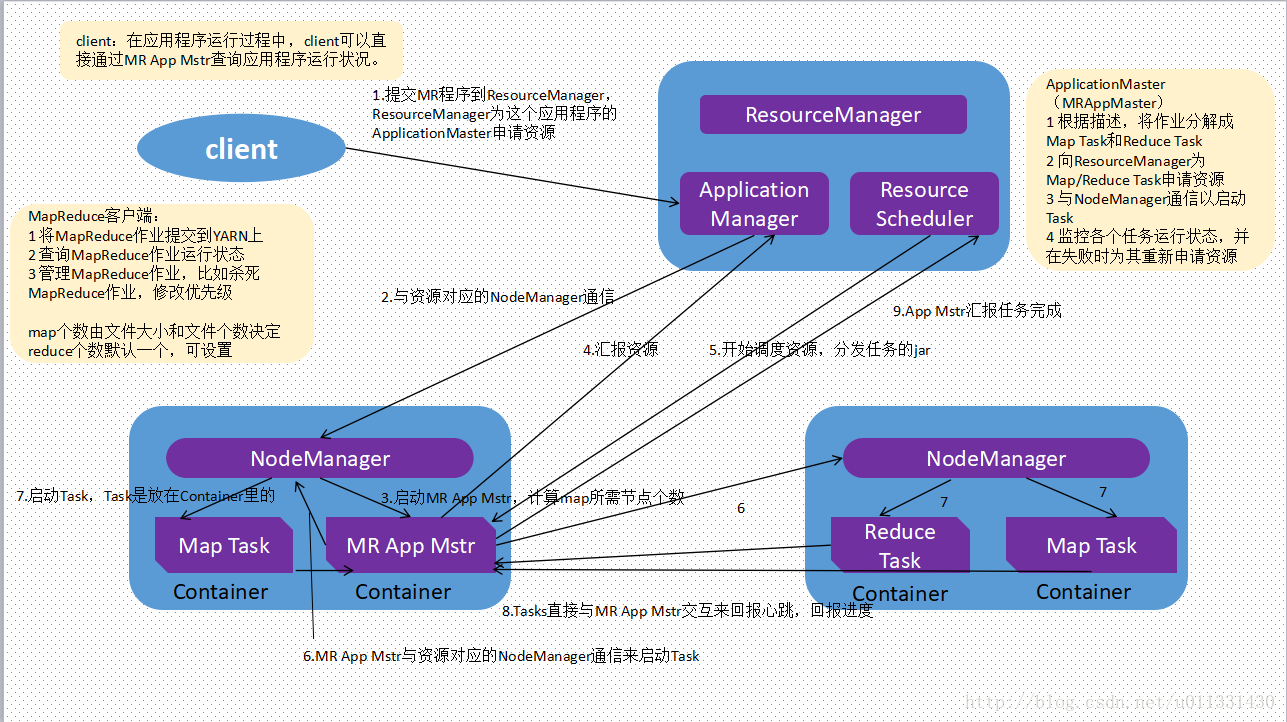
Hadoop YARN

Yet Another Resource Negotiator，通用任务、集群资源分配框架 ，面向Hadoop的编程模型

• YARN将classic/MapReduce1中Jobtracker职能划分为多个独立 实体，改善了其面临的扩展瓶颈问题

• YARN比MapReduce更具一般性，MapReduce只是YARN应用的一种 形式，可以运行Spark、Storm等其他通用计算框架

• YARN精妙的设计可以让不同的YARN应用在同一个集群上共存， 如一个MapReduce应用可以同时作为MPI应用运行，提高可管理性 和集群利用率

Hadoop MapReduce

YARN基础上的大数据集并行处理系统（框架）

• 包括两个阶段

  • Map：映射
  • Reduce：归一

• 在分布式系统上进行计算操作基本都是由Map、Reduce概念步骤 组成

  • 分布式系统，不像一般的数据库、文件系统，无法从上至下 、从头到尾进行求和等操作
  • 需要由分散的节点不断向一个点聚拢的计算过程

• 不适合实时性要求的应用，只适合大数据离线处理

Apache下Hadoop相关项目

高频

Ambari

用于部署（供应）、管理、监控Hadoop集群的Web工具

• 支持HDFS、MapReduce、Hive、HCatalog、HBase、 Oozie、ZooKeeper、Pig、Sqoop

• 提供dashboard用于查看集群健康程度，如：热度图

• 能够直观的查看MapReduce、Pig、Hive应用特点，提供 易用的方式考察其执行情况

HBase

Hadoop项目子项目，高可靠、高性能、面向列、可伸缩的分布式 存储系统

• 该技术源于Fay Chang撰写的Google论文《Bigtable：一个 结构化数据的分布式存储系统》，类似于Bigtable在Google 文件系统上提供的分布式数据存储一样，HBase在Hadoop的 基础上提供了类似于Bigtable的能力

• 适合非结构化数据存储

• 可用于在廉价PC Server上搭建大规模结构化存储集群，是 NoSQL数据库的两个首选项目（MongoDB）

Hive

基于Hadoop的数据仓库工具

• 在Hive中建立表，将表映射为结构化数据文件

• 可以通过类SQL语句直接查询数据实现简单的MapReduce统计， 而不必开发专门的MapReduce应用

  • Hive会将SQL语句转换为MapReduce任务查询Hadoop
  • 速度很慢
  • 适合数据仓库的统计分析
  • 支持SQL语法有限

Pig

基于Hadoop的大规模数据高层分析工具（类似于Hive）

• 提供SQL-Like语言PigLatin

  • 其编译器会把类SQL的数据分析请求，转换为一系列经过 优化处理的MapReduce运算

  • 是一种过程语言，和Hive中的类SQL语句相比，更适合写 脚本，而Hive的类SQL语句适合直接在命令行执行

Zookeeper

Hadoop正式子项目，针对大型分布式应用设计的分布式、开源协调 系统

• 提供功能：配置维护、名字服务、分布式同步、组服务

• 封装好复杂、易出错的关键服务，提供简单易用、功能稳定、 性能高效的接口（系统），解决分布式应用中经常遇到的数据 管理问题，简化分布式应用协调及管理难度，提供高性能分布式 服务

• 通常为HBase提供节点间的协调，部署HDFS的HA模式时是 必须的

Spark

基于内存计算的开源集群计算系统，目的是让数据分析更加快速

低频

Mahout

基于Hadoop的机器学习、数据挖掘的分布式框架

• 使用MapReduce实现了部分数据挖掘算法，解决了并行挖掘问题

  • 包括聚类、分类、推荐过滤、频繁子项挖掘

• 通过使用Hadoop库，Mahout可以有效扩展至云端

Cassandra

开源分布式NoSQL数据库系统，最初由Facebook开发，用于存储 简单格式数据，集Google BigTable数据模型和Amazon Dynamo 的完全分布式架构于一身

Avro

数据序列化系统，设计用于支持数据密集型、大批量数据交换应用， 是新的数据序列化格式、传输工具，将逐步取代Hadoop原有的 IPC机制

Chukwa

用于监控大型分布式系统的开源数据收集系统，可以将各种类型的 数据收集成适合Hadoop处理的文件，保存在HDFS中供MapReduce 操作

Tez

基于YARN的泛用数据流编程平台

• 提供强力、灵活的引擎用于执行任何DAG任务，为批处理和 交互用例处理数据

Tez正逐渐被Hive、Pig等Hadoop生态框架采用，甚至被一些 商业公司用于替代MapReduce作为底层执行引擎

其他Hadoop相关项目

高频

Sqoop

用于将Hadoop和关系型数据库中数据相互转移的开源工具

• 可以将关系型数据库（MySQL、Oracle、Postgres）中 数据转移至Hadoop的HDFS中

• 也可以将HDFS的数据转移进关系型数据库中

Impala

由Cloudera发布的实时查询开源项目

• 模仿Google Dremel

• 称比基于MapReduce的Hive SQL查询速度提升3~30倍，更加 灵活易用

Phoenix

apache顶级项目，在HBase上构建了一层关系型数据库，可以用 SQL查询HBase数据库，且速度比Impala更快，还支持包括 二级索引在内的丰富特性，借鉴了很多关系型数据库优化查询方法

Oozie

工作流引擎服务器，用于管理、协调运行在Hadoop平台 （HDFS、Pig、MapReduce）的任务

Cloudera Hue

基于Web的监控、管理系统，实现对HDFS、MapReduce/YARN、 HBase、Hive、Pig的Web化操作和管理

低频

Hama

基于HDFS的BSP(Bulk Synchronous Parallel)并行 计算框架，可以用包括图、矩阵、网络算法在内的大规模、 大数据计算

Flume

分布的、可靠的、高可用的海量日志聚合系统，可用于日志数据 收集、处理、传输

Giraph

基于Hadoop的可伸缩的分布式迭代图处理系统，灵感来自于BSP和 Google Pregel

Crunch

基于Google FlumeJava库编写的Java库，用于创建MapReduce 流水线（程序）

• 类似于Hive、Pig，提供了用于实现如连接数据、执行聚合 、排序记录等常见任务的模式库

  • 但是Crunch不强制所有输入遵循同一数据类型

  • 其使用一种定制的类型系统，非常灵活，能直接处理复杂 数据类型，如：时间序列、HDF5文件、HBase、序列化 对象（protocol buffer、Avro记录）

• 尝试简化MapReduce的思考方式

  • MapReduce有很多优点，但是对很多问题，并不是合适的 抽象级别

  • 出于性能考虑，需要将逻辑上独立的操作（数据过滤、投影 、变换）组合为一个物理上的MapReduce操作

Whirr

运行于云服务的类库（包括Hadoop），提供高度互补性

• 相对中立
• 支持AmazonEC2和Rackspace的服务

Bigtop

对Hadoop及其周边生态打包、分发、测试的工具

HCatalog

基于Hadoop的数据表、存储管理，实现中央的元数据、模式管理， 跨越Hadoop和RDBMS，利用Pig、Hive提供关系视图

Llama

让外部服务器从YARN获取资源的框架

非CDH组件

Fuse

让HDFS系统看起来像普通文件系统

Hadoop Streamin

MapReduce代码其他语言支持，包括：C/C++、Perl、Python 、Bash等

MapReduce1.0组件

MapReduce1.0是指Hadoop1.0中组件，不是指MapReduce计算模型

优势

• 方便扩展：能够运行在普通服务器构成的超大规模集群上

• IO瓶颈：通过将IO分散在大规模集群的各个节点上，可以提高 数据装载速度（大规模数据时只有部分数据可以状态在内存中）

局限

• MapReduce计算模型问题（参见MapReduce计算模型）

• 数据处理延迟大

  • MapReduce作业在Map阶段、Reduce阶段执行过程中，需要 把中间结果存盘
  • 在MR作业间也需要通过磁盘实现作业间的数据交换

• 资源利用率低

  • 任务调度方法远未达到优化资源利用率的效果，给每个 TaskTracker分配任务的过程比较简单

资源分配

• 每个TaskTracker拥有一定数量的slots，每个活动的Map、 Reduce任务占用一个slot

• JobTracker把任务分配给最靠近数据、有slot空闲TT

• 不考虑Task运算量大小，所有Task视为相同，如果有某个TT 当前负载过高，会影响整体的执行

• 也可以通过Speculative Execution模式，在多个slave上 启动同一个任务，只要其中有一个任务完成即可

执行引擎

MapReduce执行引擎运行在HDFS上

• JobTracker：运行在NameNode上

  • 分解客户端提交的job为数据处理tasks，分发给集群里相关 节点上的TaskTacker运行
  • 发送任务原则：尽量把任务推送到离数据最近的节点上， 甚至推送到数据所在的节点上运行

• TaskTracker：运行在DataNode上

  • 在节点上执行数据处理map、reduce tasks
  • 可能需要从其他DataNode中获取需要数据

MapRedudce2.0

Shuffle

Shuffle：系统执行排序的过程

• 为了确保MapReduce的输入是按键排序的

Map端

每个Map Task都有一个内存缓冲区用于存储map输出结果，缓冲区 快满时需要将缓冲区数据以临时文件方式存放到磁盘中，整个Task 结束后再对此Map Task产生所有临时作合并，生成最终正式输出文件 ，等待Reduce Task拉数据

YARN

Yet Another Resource Negotiator，通用任务、集群资源分配框架 ，面向Hadoop的编程模型

YARN优势

扩展性

• YARN将classic/MapReduce1中Jobtracker职能划分为多个独立 实体，改善了其面临的扩展瓶颈问题

• MapReduce现在只是批数据处理框架，是YARN支持的数据处理 框架的一种，独立于资源管理层，单独演化、改进

• YARN精妙的设计可以让不同的YARN应用在同一个集群上共存， 如一个MapReduce应用可以同时作为MPI应用运行，提高可管理性 、集群利用率

高效率

• ResourceManager是单独的资源管理器

• Job Scheduler指负责作业调度

• 根据资源预留要求、公平性、Service Level Agreement等标准 ，优化整个集群的资源利用

一般性

YARN是通用资源管理框架，在其上可以搭建多种数据处理框架

• 批处理：MapReduce
• 交互式处理：Tez
• 迭代处理：Spark
• 实时流处理：Storm
• 图数据处理：GraphLab/Giraph

YARN中实体

ResourceManager

RM物理上对应主节点，逻辑上管理集群上的资源使用，其功能由 Scheduler、ApplicationManager协调完成

• AppplicatonManager：接受、监控任务

  • 接受客户端提交的job

  • 判断启动该job的ApplicationMaster所需的资源

  • 监控ApplicationMaster的状态，并在失败时重启其

• Scheduler：分配资源、调度

  • Schedular计算启动ApplicationManager提交的job的AM所需 资源，将资源封装成Container

  • 然后根据调度算法调度，在某个NM上启动job的AM

  • 不提供失败重启、监控功能

  • Scheduler收到AM任务完成汇报之后，回收资源、向RM返回 执行结果

  • 调度算法可自定以，YARN根据不同场景提供

    • FIFO Scheduler
    • Capacity Scheduler
    • Fair Scheduler

NodeManager

NM物理上对应计算节点，逻辑上监控、管理当前节点资源

• 仅仅抽象本节点资源（cpu、内存、磁盘、网络等），并且定时 像RM的Scheduler汇报

• 接受并处理AM的tasks启动、停止等请求

ApplicationMaster

AM管理集群上运行任务生命周期

• 每个job都有一个专用的AM

• AM启动后会计算job所需资源，并向Scheduler申请资源

• AM运行在job运行期间，负责整个job执行过程的监控

  • NM分配完任务container后，AM开始监控这些containers 、tasks状态
  • 任务失败则回收资源重新生成
  • 成功则释放资源
  • 任务执行完毕后回报Scheduler

Containers

YARN为将来的资源隔离提出的框架，是一组资源的集合，每个task 对应一个container，只能在container中运行

• 容器有特定的内存分配范围

  • 容器内存最小值即为内存分配单位，内存最大值也应该是 内存分配单位整数倍

  • 根据任务所需资源多少分配给容器整数倍内存单位，但是 如果任务所需内存大于容器内存最大值，运行时可能会报错

• 由NM确保task使用的资源不会超过分配的资源

• 注意

  • AM并不运行于container中，真正的task才运行在container

Job运行过程

作业提交

• 从RM获取新的作业ID
• 作业客户端检查作业输出说明，计算输入分片（也可以配置 在集群中产生分片）
• 将作业资源复制到HDFS
• 调用RM上的submitApplication方法提交作业

作业初始化

1. RM收到调用submitApplication消息后，将请求传递给 内部scheduler，scheduler分配一个container
2. NM在RM的管理下在容器中启动应用程序的master进程AM， 其对作业进行初始化
3. AM创建多个簿记对象用于接受任务进度、完成报告，保持 对作业进度的跟踪
4. AM接受来自共享文件系统的在客户端计算的输入分片，对 每个分片创建一个map对象，及由mapreduce.job.reduces 属性确定的多个reduce任务对象
5. AM根据任务大小决定如何运行job，如果在新容器中分配、 运行任务的开销大于并行运行时的开销，AM会在单个节点 上运行，这样的作业称为uberized
6. AM在任何tasks执行之前通过job的setup方法设置job的 OutputCommiter，建立作业输出目录

任务分配

1. 若作业不适合作为uber任务运行，AM为该作业中所有map 、reduce任务向RM请求容器
2. 请求附着heart beat，包括每个map任务的数据本地化信息 ，特别是输入分片所在的主机、机架信息，scheduler据此 做调度决策
   • 理想化情况下任务分配到数据本地化节点
   • 否则优先使用机架本地化
3. 请求同时指定了任务内存需求，YARN中的资源分为更细粒度 ，task可以请求最小到最大限制范围、任意最小值倍数的 内存容量

任务执行

1. 当NM的scheduler为task分配了container，AM就可以通过 与NM通信启动容器
2. 任务由YarnChild执行，在执行任务之前，需要将任务 所需资源本地化，包括作业的配置、JAR文件、所有来自 分布式缓存的文件，然后运行map、reduce任务
3. 对于Streaming、Pipes程序，YarnChild启动Streaming、 Pipes进程，使用标准输入输出、socket与其通信（以 MapReduce1方式运行）

进度和状态更新

1. task每3s通过umbilical接口向AM汇报进度、状态（包括 计数器），作为job的aggregate view
2. 客户端则默认没1s查询AM接受进度更新

作业完成

1. 客户端每5s通过调用job的waitForCompletion检查作业 是否完成，也可以通过HTTP callback完成作业
2. 作业完成后AM和task容器清理工作状态，OutputCommiter 作业清理方法被调用

todo：这里逻辑有问题，要删

MapReduce计算模型

• 分布式系统，不像一般的数据库、文件系统，无法从上至下 、从头到尾进行求和等操作
• 需要由分散的节点不断向一个点聚拢的计算过程，即分布式系统 上计算模型基本都是由map、reduce步骤组成

MapReduce

MapReduce每步数据处理流程包括两个阶段

• Map：映射

  • map过程相互独立、各mapper见不通信，所以mapreduce 只适合处理独立计算的任务

• Reduce：归一

  • reduce直接处理map的输出，reduce的键为map输出 值

数据处理过程

• 需要把任何计算任务转换为一系列MapReduce作业，然后依次 执行这些作业

• 计算过程的各个步骤之间，各个作业输出的中间结果需要存盘， 然后才能被下个步骤使用（因为各个步骤之间没有明确流程）

• One Pass Computation：只需要一遍扫描处理的计算任务 MapReduce计算模型非常有效

• Multi Pass Computation：需要在数据上进行多遍扫描、处理 的计算任务，需要执行多个MapReduce作业计算任务，因为 多副本复制、磁盘存取，其效率不高

Mapred on DAG

Directed Acyclic Graph；表示数据处理流程的有向无环图

• 顶点：数据处理任务，反映一定的业务逻辑，即如何对数据进行 转换和分析
• 边：数据在不同的顶点间的传递

比较

• 正是MapReduce提供操作原语少、抽象层次低，所以其表达能力 差，同时需要用户处理更多的逻辑，易用性、可读性差

  • 复杂数据处理任务，如：机器学习算法、SQL连接查询很难 表示用MapReduce计算默认表达

  • 操作原语多并不是DAG本身的要求，DAG本身只是有向无环图， 只是使用DAG计算模型可以提供更多的操作原语

• 由于DAG的表达能力强于MapReduce，对某些处理逻辑，DAG 所需作业数目小于MapReduce，消除不必要的任务

  • DAG显著提高了数据处理效率，对小规模、低延迟和大规模、 高吞吐量的负载均有效

  • MapReduce需要通过把中间结果存盘实现同步，而DAG整合 部分MapReduce作业，减少磁盘I/O

  • reduce任务需要等待map任务全部完成才能继续，DAG优化 数据处理流程，减少同步Barrier

• DAG部分计算模型也由map、reduce任务构成，只是不像传统 MapReduce计算模型中map、reduce必须成对出现

  • 或者说DAG只有一次map任务（扫描数据时），其余都是 reduce任务？

  • 从MapReduce配置也可以看出，MapReduce可以选择基于 yarn或yarn-tez

Tez简介

Tezm目标就是建立执行框架，支持大数据上DAG表达的作业处理

• YARN将资源管理功能从数据处理模型中独立出来，使得在Hadoop 执行DAG表达的作业处理成为可能，Tez成为可扩展、高效的执行 引擎

  • Tez在YARN和Hive、Pig之间提供一种通用数据处理模型DAG
  • Hive、Pig、Cascading作业在Tez上执行更快，提供交互式 查询响应

• Tez把DAG的每个顶点建模为Input、Processer、Output模块的 组合

  • Input、Output决定数据格式、输入、输出
  • Processor包装了数据转换、处理逻辑
  • Processor通过Input从其他顶点、管道获取数据输入，通过 Output向其他顶点、管道传送生成数据
  • 通过把不同的Input、Processor、Output模块组合成顶点， 建立DAG数据处理工作流，执行特定数据处理逻辑

• Tez自动把DAG映射到物理资源，将其逻辑表示扩展为物理表示， 并执行其中的业务逻辑

  • Tez能为每个节点增加并行性，即使用多个任务执行节点 的计算任务

  • Tez能动态地优化DAG执行过程，能够根据执行过程中获得地 信息，如：数据采样，优化DAG执行计划，优化资源使用、 提高性能

    • 去除了连续作业之间的写屏障
    • 去除了工作流中多余的Map阶段

Tez执行过程

• 初始化例程，提供context/configuration信息给Tez runtime

• 对每个顶点的每个任务（任务数量根据并行度创建）进行初始化

• 执行任务Processor直到所有任务完成，则节点完成

• Output把从Processor接收到的数据，通过管道传递给下游顶点 的Input

• 直到整个DAG所有节点任务执行完毕

访问其他数据库服务器

SQL默认阻止对组件Ad Hoc Distributed Queries的STATEMENT OpenRowSet/OpenDatasource的访问，需要使用sp_configure 启用Ad Hoc Distributed Queries

• 开启Ad Hoc Distributed Queries

  1 2 3 4

  exec sp_configure 'show advanced options',1 reconfigure exec sp_configure 'Ad Hoc Distributed Queries',1 reconfigure

• 关闭

  1 2 3 4

  exec sp_configure 'Ad Hoc Distributed Queries',0 reconfigure exec sp_configure 'show advanced options',0 reconfigure

特殊语法

数据导入

• mssql中换行符设置为\n表示的是\r\n，即永远无法单独 指定\n或者\r，尽量使用ASCII码0xXX表示

  1	> bulk insert tbl_name from /path/to/file with (FILEDTERMINATOR="|", ROWTERMINATOR="0x0a");

数据迁移

直接查询、插入

同库

1
2

insert into dst_tb select * from src_tb;
insert into dst_tb(field1, field2, ...) select (field_a, field_b, ...) from src_tb;

异库、同服务器

1
2
3
4
5
6

insert into db1.dst_db select * from db2.src_db;
	# 插入已有表
create table db1.dst_tb as select * from db2.src_tb;
	# 创建表并插入数据
rename table src_db.src_tb to dst_db.dst_tb;
	# 重命名迁移完整表

异服务器

文件中介、跨实例

.sql

1
2
3
4
5

$ mysqldump [-u user] -p --single-transaction [--where=""] src_db src_tb > src_db.src_tb.sql
	# 导入数据
	# 加上`-d`仅导出表结构
$ mysql [-u user] -p dst_db < src_db.src_tb.sql
	# 导入数据

1

source src_db.src_tb.sql;

.csv

secure_file_priv

load data infile和into outfile需要mysql开启 secure_file_priv选项，可以通过查看

1

show global variables like `%secure%`;

mysql默认值NULL不允许执行，需要更改配置文件

1
2

[mysqld]
secure_file_priv=''

本机Server

1
2
3
4
5
6
7
8
9
10
11
12
13
14

select * from src_tb into outfile file_name.csv
	fields terminated by ','
	optionally enclosed by '"'
	escaped by '"'
	lines terminated by '\r\n';
	# 导出至`.csv`

load data infile file_name.csv [replace] into table dst_tb(field1, field2, @dummy...)
	fields terminated by ','
	optionally enclosed by '"'
	escaped by '"'
	lines terminated by '\r\n';
	# 从`.csv`数据导入
	# 表结构不同时可以设置对应字段，多余字段`@dummy`表示丢弃

异机Server

1
2
3
4

$ mysql -h host -u user -p src_db -N -e "select * from src_tb;" > file_name.csv
	# 只能通过*shell*查询并导出至文件
	# 需要`file`权限
	# `-N`：skip column names

1
2

load data local infile filename.csv;
	# 指定`local`则从*client*读取文件，否则从*server*读取

大表分块迁移

• 容易分块的字段
  • 自增id
  • 时间

注意

综述

• 数组、广义表可以看作是线性表的扩展：线性表中数据元素本身 也是抽象数据结构

Array

对各维界分别为$b_i$的n维数组

• 数组中含有$\prod_{i=1}^n b_i$个数据元素，每个元素都受n个 关系约束

  • 每个关系中，元素都有直接后继
  • 就单个关系而言，这个n个关系仍然是线性关系

• n维数组可看作是线性表的推广，n=1时，数组退化为定长线性表

  • 和线性表一样，所有数据元素必须为同一数据类型

• 数组一旦被定义，其维数、维界就不再改变

  • 除了初始化、销毁之外，数组只有存储、修改元素值的操作
  • 采用顺序存储结构表示数组是自然的

• 几乎所有程序设计语言都把数组类型设定为固有类型

顺序存储表示

• 存储单元是一维结构，数组是多维结构，所有使用连续存储单元 存储数组的数据元素需要约定次序

  • BASIC、PL/1、COBOL、PASCAL、C语言中，以行序作主序
  • FORTRAN中，以列序作主序

• 数组元素存储地址

  $$\begin{align*} LOC(j_1, j_2, \cdots, j_n) & = LOC(0, 0, \cdots, 0) + (\sum_{i=1}^{n-1} j_i (\prod_{k=i+1}^n b_k + j_n))L & = LOC(0, 0, \cdots, 0) + \sum_{i=1}^n c_i_i \end{align}$$

  • $cn=L, c{i-1} = b_ic_i$

1
2
3
4
5
6
7
8
9

typedef struct{
	Elemtype * base;
	int dim;
		// 数组维数
	int * bounds;
		// 数组各维界（各维度长度）
	int * constants;
		// 数组各维度单位含有的数组元素数量，由`bounds`累乘
}

矩阵压缩

压缩存储：为多个值相同元只分配一个存储空间，对0元不分配空间

特殊矩阵

特殊矩阵：值相同元素、0元素在矩阵的分布有一定规律，将其压缩 至一维数组中，并找到每个非零元在一维数组中的对应关系

• 对称矩阵：为每对对称元分配一个存储空间
  • 一般以行序为主序存储其下三角（包括对角线）中的元
• 上/下三角矩阵：类似对称矩阵只存储上/下三角中的元，附加 存储下/三角常数
• 对角矩阵：同样可以按照行、列、对角线优先压缩存储

稀疏矩阵

稀疏矩阵：稀疏因子$\sigma = \frac t {mn} \leq 0.05$的矩阵

• 使用三元组（非零元值、其所属的行列位置）表示非零元

三元组顺序表

三元组顺序表/有序双下标法：以顺序结构表示三元组表

1
2
3
4
5
6
7
8
9

typedef struct{
	int i, j;
	ElemType e;
}Triple;
typedef struct{
	Triple data[MAXSIZE+1];
	int mu, nu, tu;
		// 行、列、非零元数
}TSMatrix;

• data域中非零元的三元组以行序为主序顺序排列，有利于进行 依行顺序处理的矩阵运算

行逻辑链接的顺序表

行逻辑链接的顺序表：带行链接信息的三元组表

1
2
3
4
5
6

typedef struct{
	Triple data[MAXSIZE+1];
	int rpos[MAXRC+1];
		// 各行首个非零元的位置表
	int mu, nu, tu;
}RLSMatrix;

• 为了便于随机存取任意行非零元，需要知道每行首个去非零元 在三元组表中的位置，即rpos

十字链表

十字链表：采用链式存储结构表示三元组的线性表

1
2
3
4
5
6
7
8
9
10
11
12

typedef struct OLNode{
	int i,j;
		// 该非零元行、列下标
	ElemType e;
	struct OLNode, *right, *down;
		// 该非零元所在行表、列表的后继链域
}OLNode, *OLink;
typedef struct{
	OLink *rhead, *chead;
		// 行、列链表表头指针向量基址
	int mu, nu, tu;
}CrossList;

• 同一行非零元通过right域链接成一个线性链表
• 同一列非零元通过down域链接成一个线性链表

• 适合矩阵非零元个数、位置在操作过程中变化较大的情况

Lists

广义表/列表：线性表的推广

• $\alpha_i$：可以时单个元素，也可以是广义表，分别称为LS 的原子、子表
• head：表头，LS非空时的首个元素$\alpha$
• tail：表尾，LS除表头外的其余元素组成的表，必然是列表

• 列表是一个多层次结构：列表的元素可以是子表，子表元素 也可以是子表
• 列表可以为其他列表所共享
• 列表可以是一个递归的表：即列表自身作为其本身子表

• 广义表长度：广义表中元素个数
• 广义表深度：广义表中最大括弧重数

链式存储结构

广义表中数据元素可以具有不同结构，难以用顺序存储结构表示， 通常采用链式存储结构

头尾链表

• 数据元素可能是原子、列表，因此需要两种结构的结点
  • 表节点：表示列表，包括：标志域、指示表头的指针域、 指示表尾的指针域
  • 原子节点：表示原子，包括：标志域，值域

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

typedef enum{ATOM, LIST} ElemTag;

typedef struct GLNode{
	ElemTag tag;
		// 标志域，公用
	union{
		// 原子节点、表节点联合部分
		AtomType atom;
			// 值域，原子节点
		struct{
			struct GLNode *hp, *tp;
				// 两个指针域，表节点
		}ptr;
	};
}*GList;

• 除空表的表头指针为空外，任何非空列表的表头指针均指向 表节点，且该表节点
  • hp指针域指向列表表头
  • tp指针域指向列表表尾，除非表尾为空，否则指向表节点
• 容易分清列表中原子、子表所属层次
• 最高层的表节点个数即为列表长度

扩展线性链表

1
2
3
4
5
6
7
8
9
10

typedef enum {ATOM, LIST} ElemTag;

typedef struct GLNode{
	ElemTag tag;
	union{
		AtomType atom;
		struct GLNode *hp;
		};
	struct GLNode *tp;
}*GList;

• 从数据结构来看，栈和队列也是线性表，但其基本操作是线性表 操作的子集
• 从数据类型来看，栈和队列是和线性表不同的抽象数据类型

Stack

栈：限定在表尾/栈顶进行插入和删除、操作受限的线性表

• top：栈顶，表尾端
• bottom：栈底，表头端

• 栈的修改是按照LIFO的方式运转，又称后进先出的线性表

  • 入栈：插入元素
  • 出栈：删除栈顶元素

• last in first out/栈应用广泛，对实现递归操作必不可少

顺序存储结构

顺序栈

顺序栈：顺序映像存储栈底到栈顶的数据元素，同时附设指针指示 栈顶元素在顺序栈帧中的位置

1
2
3
4
5

typedef struct{
	SElemType * base;
	SElemType *top;
	int stacksize;
}SqStack;

• base永远指向栈底，top指向栈顶元素下个位置

  • base==NULL：栈不存在
  • top==base：表示空栈

• 栈在使用过程中所需最大空间难以估计，因此一般初始化设空栈 时不应限定栈的最大容量，应分配基本容量，逐渐增加

链式存储结构

Queue

队列：限定在表尾/队尾进行插入、在表头/队头进行删除的 受限线性表

• rear：队尾，允许插入的一端
• front：队头，允许删除的一端

• 队列是一种FIFO的线性表
• 队列在程序设计中经常出现
  • 操作系统作业排队
  • 图的广度优先遍历

链式存储结构

链队列

链队列：使用链表表示的队列

1
2
3
4
5
6
7
8

typedef struct QNode{
	QElemType data;
	struct QNode  * next;
}QNode, *QueuePtr;
typedef struct{
	QueuePtr front;
	QueuePtr rear;
}LinkQueue;

• front：头指针
• rear：尾指针

• 为方便同样给链队列添加头结点，令头指针指向头结点，此时 空队列判断条件为头、尾指针均指向头结点
• 链队列的操作即为单链表插入、删除操作的特殊情况的，需要 同时修改头、尾指针

顺序存储结构

循环队列

循环队列：使用顺序结构存储队列元素，附设两个指针分别指示对头 、队尾的位置

• 为充分利用数组空间，将数组视为环状空间

1
2
3
4
5

typedef struct{
	QElemType * base;
	int front;
	int rear;
}

• front：头指针
• rear：尾指针
• 循环队列时，无法通过rear==front判断队列空、满，可以在 环上、环外设置标志位判断

• C语言中无法用动态分配的一维数组实现循环队列，必须设置 最大队列长度，如果无法确定，应该使用链队列

Deque

双端队列：限定删除、插入操作在表两端进行的线性表

• 输出受限双端队列：一个端点允许删除、插入，另一个端点只 允许插入
• 输入受限双端队列：一个端点允许删除、插入，另一个端点只 允许删除
• 栈底邻接的两个栈：限定某个端点插入元素只能从该端点删除

• 看起了灵活，但是实际应用不多

Priority Queue优先队列

• 用于从一个动态改变的候选集合中选择一个优先级高的元素
• 主要操作
  • 查找、删除最大元素
  • 插入元素
• 实现
  • 可以基于数组、有序数组实现
  • 基于heap的优先队列实现更好

综述

串/字符串：零个或多个字符组成的有限序列

• 文本串：字母、数字、特殊符号构成
• 位串：0、1构成
• 基因序列：可以使用字符串模型表示，其字母表只包括4个 字母{A, C, G, T}

• $s$：串名，其后单引号括起是串的值
• $a_i$：字母、数字等字符
• $n$：串中字符的数目，串长度，零个字符的串称为空串

• 串的逻辑结构和线性表相似，只是串的数据对象约束为字符集
• 串的基本操作和线性表有很大差别
  • 线性表基本操作大多以“单个元素”作为操作对象
  • 串的基本操作通常以“串的整体”作为操作对象

串的存储表示

• 串只作为输入、输出常量出现，则只需要存储串的串值字符序列
• 在非数值处理中，串也以变量形式出现

定长顺序存储

• 类似线性表的顺序存储结构
• 按照预定义大小，为每个定义的串变量分配固定长度的存储区， 存储字符序列

1

typedef unsigned char SString[MAXSTRLEN+1]

• 串实际长度在预定义范围内随意，超过预定义长度的串值则被 舍去（截断）
• 串实际长度存储方式
  • 以下标为0的数组分量存放：Pascal
  • 在串值后面加入不计串长的结束标记字符：C以\0标记， 此时串长为隐含值，不利于某些操作
• 串操作的原操作为“字符序列的复制”，操作的时间复杂度基于 复制的字符序列长度

堆分配存储

• 仍然以地址连续的存储单元存储串字符序列，但存储空间是在 程序执行过程中动态分配得到

1
2
3
4

typdef struct{
	char *ch;
	int length;
}

• length：串长

• 既有顺序存储结构的特点，处理方便，对串长又没有任何限制
• 此存储结构的串操作仍是基于“字符序列的复制”进行

块链存储

• 使用链表的方式存储串值
• 但是串结构特殊的，需要设置节点大小

1
2
3
4
5
6
7
8

typedef struct Chunk{
	char ch[CHUNKSIZE];
	struct CHUNK * next;
}Chunk;
typedef struct{
	Chunk *head, *tail;
	int curlen;
}

• CHUNKSIZE：节点大小，每个节点中最大存储字符数量
• curlen：当前串长度

• 节点大小不为1时，链表最后一个节点不一定全被串值占满， 此时通常补上非串值字符
• 一般情况下，对串进行操作时，只需要从头到尾扫描即可
  • 对串值不必简历双向链表
  • 设尾指针是为了方便进行联结操作（联结操作需要注意 串尾无效字符）
• 节点大小选择影响串处理效率
  • 存储效率 = 串值所占存储位/实际分配存储位
  • 存储密度小，运算处理方便，存储量占用大
• 块链结构对某些串操作有一定方便，但是总的来说不如另外两种 存储结构灵活，存储量大、操作复杂

串的模式匹配

模式匹配：子串定位操作

总述

处理类似于点、线、多面体这样的几何对象

最近对问题

给定平面上的n个点中，距离最近的两个点

• 点数量n不大3时，可以通过蛮力算法求解的
• 假设集合中每个点均不相同、点按其x坐标升序排列
• 另外使用算法得到点按照y坐标升序排列的列表Q

蛮力算法

算法

1
2
3
4
5
6
7
8
9

BruteForceClosestPoints(p)
	// 蛮力算法求平面中距离最近的点
	// 输入：n个点的列表p；p_i = (x_i, y_i)
	// 输出：两个最近点的距离
	d = \infty
	for i = 1 to n -1 do
		for j = i+1 to n do
			d = min(d, sqrt((x_i - x_j)^2 + (y_i - y_j)^2))
	return d

改进

• 忽略平方根函数，只比较平方

分治法

• 在点集在x轴方向中位数m作垂线，将点集分成大小为 $\lceiling n/2 \rceiling, \lfloor n/2 \rfloor$两个子集 $P_l, P_r$，然后递归求解子问题$P_l, P_r$得到最近点问题解

• 定义$d=min{d_l, d_r}$

  • d不一定是所有点对最小距离
  • 最小距离点对可能分别位于分界线两侧，在合并子问题的 解时需要考虑

• 只需要考虑关于m对称的2d垂直带中的点，记S为来自Q、位于 分隔带中的点列表

  • S同样升序排列
  • 扫描S，遇到距离更近的点对时更新最小距离$d_{min}=d$
  • 对于S中点P，只需考虑在其后、y坐标差小于$d_min$ 的矩形范围内点（因为S有序，P前的点已经考虑过）
  • 该矩形范围内点数目不超过6个（包括P），所以考虑下个点 前，至多考虑5个点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

EfficientClosestPair(P, Q)
	// 分治法解决最近点问题
	// 输入：P存储平面上n个点，按x轴坐标升序排列
			Q存储和P相同的n个点，按y坐标升序排列
	/// 输出：最近点直接欧几里得距离
	if n <= 3
		return 蛮力法最小距离
	else
		将P前ceiling(n/2)个点复制到P_l
		将Q相应的ceiling(n/2)点复制到Q_l
		将P余下floor(n/2)个点复制到P_r
		将Q余下floor(n/2)个点复制到Q_r

		d_l = EfficientClosestPair(P_l, Q_l)
		d_r = EfficientClosestPair(P_r, Q_r)
		d = min{d_l, d_r}

		m = P[ceiling(n/2) - 1].x
		将Q中所有|x-m|<d的点复制到数组S[0..num-1]

		dminsq = d^2
		for i=0 to num-2 do
			k = i+1
			while k <= num-1 and (S[k].y - S[i].y)^2 < dminsq
				dminsq = min((S[k].x - S[i].x)^2 + (S[k].y - S[i].y)^2, dminsq)
				k = k+1
	return sqrt(dminsq)

算法特点

• 算法时间效率

  • 将问题划分为规模相同子问题、合并子问题解，算法都只 需要线性时间
  • 运行时间递推式$T(n) = 2T(n/2) + f(n)$，其中 $f(n) \in \Theta(n)$，则$T(n) \in \Theta(nlogn)$
  • 已经证明在对算法可以执行的操作没有特殊假设情况下， 这是可能得到的最好效率

应用

• 聚类分析

凸包问题

寻找能把给定集合中所有点都包含在里面的最小凸多边形

• 设集合S中点按照x坐标升序排列，存储在列表P中 （x坐标相同，按y坐标升序）

蛮力算法

算法

• 对于n个点集中两个点$p_i$、$p_j$，当且仅当集合中其他点 都位于穿过这两点的直线同侧时，其连线是该集合凸包边界 一部分
• 检验每对点，满足条件的点即构成凸包边界

特点

• 算法时间效率为$O(n^3)$

快包算法（分治法）

算法

• $p_1、$p_n$显然是凸包顶点，且$\overrightarrow{p_1p_n}$ 将点集分为左右两部分$S_1$、$S_2$

  • 其上的点不是凸包顶点，之后不必考虑
  • S的凸包也被划分为upper hull、lower hull，可以使用 相同的方法构造

• 若$S1$为空，则上包就是线段$p_1p_n$；否则寻找距离 $p_1p_n$最大点$p{max}$，若有多个，则选择使得夹角 $\angle p_{max}p_1p_n$最大点

  • $p_max$是上包顶点
  • 包含在$\triangle p1p{max}p_2$中的点不是上包顶点， 之后不必考虑
  • 不存在同时位于$\overrightarrow{p1p{max}}$、 $\overrightarrow{p_{max}p_n}$左侧的点

• 对$\overrightarrow{p1p{max}}$及其左侧点构成的集合 $S{1,1}$、$\overrightarrow{p{max}pn}$及其左侧的点构成 集合$S{1,2}$，重复以上即可继续得到上包顶点

• 类似的可以对$S_2$寻找下包顶点

向量左侧、距离计算参考线代

算法特点

快包和快排很类似

• 最差效率$\Theta(n)$，平均效率好得多
• 也一般会把问题平均的分成两个较小子问题，提高效率
• 对于均匀分布在某些凸区域（园、矩形）的点，快包平均效率 可以达到线性

应用

• 计算机动画中使用凸包替换物体本身，加快碰撞检测速度
• 车辆路径规划
• 地理信息系统中根据卫星图像计算accessibility map
• 数理统计中用于进行异常值检测
• 计算点集直径的高效算法中需要用到

欧几里得最小生成树问题

给定平面上n个点，构造顶点为这n个点的总长度最小的树

参考

二维散点

Convex Hull

凸包：包含点集S的最小凸集合

• 离散点集：包含所有点的最小凸多边形
• 最小：凸包一定是所有包含S的凸集合的子集
• 凸包能方便地提供目标形状或给定数据集地一个近似

Extreme Point

极点：对于任何以集合中点为端点的线段，不是线段中点的点

• 极点有一些特性是凸集中其他点不具备的性质

  • 单纯形法：如果存在极值，则一定可以在极点处取到
  • 找到极点、极点排序方向即可解决凸包问题

• 举例

  • 三角形中3个顶点
  • 圆周上所有点

总述

涉及连续性数学问题

• 解方程、方程组，计算定积分，函数求值
• 和离散数学中：图、树、排序、组合相对

特点

• 大部分此类问题只能近似求解

  • 泰勒展开求解$e^x$
  • Composite Trapezoidal rule：组合梯形法则，计算 定积分

• 此类问题大部分要操作实数，而实数在计算机内部只能近似表示 ，大量对近近似数的算术操作可能会叠加误差，输出错误结果

整数乘法

俄式乘法

两个正整数n、m相乘的非主流算法

算法

• 反复应用以下公式，简化每步的计算 $$n为奇数：n * m = \frac n 2 * 2m + m \\ n为偶数：n * m = \frac n 2 * 2m$$
• 以$1 * m$作为算法终止条件

特点

• n为奇数步骤中的m，可以最后累加即可

• 算法中只有折半、加倍、相加操作

  • 手动计算非常简便
  • 计算机硬件对折半、加倍只需要移位就可

• 减常因子法

大整数乘法

算法

考虑a、b两个n位整数，n为偶数

• 从中间把数字分段，得到$a_1, a_0, b_1, b_0$

• 则有

  $$\begin{align} c & = a * b = (a_1 10^{n/2} + a_0) * (b_1 10^{n/2} + b_0) \\ & = (a_1 * b_1)10^n + (a_1 * b_0 + a_0 * b_1) 10^{n/2} + (a_0 + b_0) \\ & = c_2 10^n + c_1 10^{n/2} + c_0 \end{align}$$
  • $c_2 = a_1 * b_1$
  • $c_0 = a_0 * b_0$
  • $c_1 = (a_1 + a_0) * (b_1 + b_0) - (c_2 + c_0)

• 若n/2也是偶数，可以使用相同的方法计算得到三个乘法表达式

  • 若n为2的幂次，就可以得到计算n位数积的递归乘法
  • n迭代到足够小时，递归就可以停止

特点

• 算法效率

  • 乘法次数递推式：$M(n)=3M(n/2), M(1)=1$，则 $M(n) = n^(log_2 3) \approx n^{1.585}$
  • 加法次数递推式：$A(n)=3A(n/2) + cn, A(1)=1$，则 $A(n) \in \Theta(n^{log_2 3})$

• 算法有渐进效率优势，实际性能依赖于计算机系统、算法实现 质量，在某些情况下

  • 计算8位乘法时，分治算法速度快于传统方法
  • 计算超过100位时，速度是传统算法2倍

• 分治法

欧几里得算法

计算最大公约数、最大公倍数

最大公约数

• n为0，返回m作为结果结束
• 将m处以n的余数赋给r
• 将n付给m，r赋给n，返回第一步

1
2
3
4
5
6

Euclid(m, n)
	while n != 0 do
		r = m mod n
		m = n
		n = r
	return m

最大公倍数

• 利用最大公约数计算最小公倍数

特点

• 变治法（+减可变规模）

特定点求值

霍纳法则（计算多项式）

霍纳法则：不断将x作为公因子提取出来，合并降次后的项，然后 计算多项式在特定点的值

算法

1
2
3
4
5
6
7
8

Horner(P[0..n], x)
	// 用霍纳法则求多项式在给定点的值
	// 输入：多项式系数数组P[0..n]、数字x
	// 输出：多项式在x点的值
	p = P[n]
	for i = n-1 downto 0 do
		p = x*p + P[i]
	return p

特点

• 算法效率

  • 效率始终为n，只相当于直接计算中$a_n x^n$的乘法数量

• 变治法

二进制（计算）幂

将幂次转换为二进制位串，利用二进制位串简化计算

从左至右二进制幂

• 对位串应用霍纳法则

1
2
3
4
5
6
7
8
9
10

LeftRightBinaryExponentiation(a, B[0..n-1])
	// 从左至右二进制幂算法计算a^n
	// 输入：数字a、表示幂次的二级制位串B[0..n-1]
	// 输出：a^n的值
	product = a
	for i = n-1 downto 0 do
		product = product * product
		if B[i] == 1:
			prduct = product * a
	return product

从右至左二进制幂

• 累次计算二进制位串中为1部分值，将其累乘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

RightLeftBinaryExponentiation(a, B[0..n-1])
	// 从右至左二进制幂算法
	// 输入：数字a、表示幂次的二级制位串B[0..n-1]
	// 输出：a^n的值
	term = a
	if B[0] == 1
		product = a
	else
		product = 1
		// 保存累乘值
	for i = i to n do
		term *= 2
		// 保存二进制位为1部分值
		if B[i] = 1
			product = product * term
	return product

特点

• 算法效率

  • 两个算法效率取决于位串长度，是对数级的

• 变治法

应用

• 在密码技术中，需要对超过100位十进制整数进行乘法运算，而 计算机往往不能直接运算

矩阵乘法

Strassen矩阵乘法

算法

若A、B是两个n阶方阵（若n不是2幂次，考虑填充0）

• 将A、B、C均分块为4个n/2子矩阵
• 递归使用Strassen方程中定义的矩阵M进行计算计算C各个子阵

算法特点

• 对2 * 2分块计算，Strassen算法执行了7次乘法、18次加减法， 蛮力算法需要执行8次乘法、4次加法

• 算法效率

  • 乘法次数递推式：$M(n) = 7M(n/2), M(1) = 1$，则 $M(n) = 7^{log2 n} = n^{log_2 7} \approx n{2.807}$
  • 加法次数递推式：$A(n) = 7A(n/2) + 18(n/2)^2, A(1)=0$ ，则$A(n) \in \Theta(n^{log_2 7})$
  • 矩阵趋于无穷大时，算法表现出的渐进效率卓越

• 还有一些算法能运行时间$\in \Theta(n^\alpha)$，最小能达到 2.376，但是这些算法乘法常量很大、算法复杂，没有实用价值

• 矩阵乘法效率下界为$n^2$，目前得到的最优效率和其还有很大 距离

• 分治法

线性方程组

• 假设方程组系数矩阵为n阶方阵，且解唯一
• 主要思想都是高斯消元法（变治法），只是出于效率、误差有 不同实现方式

前向消去法

算法

1
2
3
4
5
6
7
8
9
10
11

ForwardElimination(A[1..n, 1..n], b[1..n])
	// 对方程组扩展矩阵[A|b]使用高斯消元法
	// 输入：矩阵A[1..n, 1..n]，向量b[1..n]
	// 输出：扩展的上三角矩阵
	for i = 1 to n do
		A[i, n+1] = b[i]
		// 得到扩展矩阵
	for i = 1 to n-1 do
		for j = i+1 to n do
			for k = n+1 downto i do
				A[j, k] = A[j, k] - A[i, k]*A[j, i] / A[i, i]

算法特点

• 前向消去法不一定正确

  • 如果A[i, i]==0，不能以其作为除数，此时需要交换行 （解唯一时总是存在非0行）
  • A[i, i]非常小，导致比例因子A[j, i] / A[i, i]非常大， 产生大的舍入误差

• 最内层循环效率低

部分选主元法

算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

BetterForwardElimination(A[1..n, 1..n], b[1..n])
	// 用部分选主元法实现高斯消去
	// 输入：矩阵A[1..n, 1..n]，向量b[1..n]
	// 输出：扩展的上三角矩阵
	for i = 1 to n do
		A[i, n+1] = b[i]
	for i = 1 to n-1 do
		pivotrow = i
		for j = i+1 to n do
			if |A[j, i]| > A[pivot, i]
				pivotrow = j
				// 选择第i列系数最大的行作为第i次迭代基点
				// 保证比例因子绝对值不会大于1
			for k = i to n+1 do
				swap(A[i, k], A[pivot, k])
			for j = j+1 to n do
				temp = A[j, i] / A[i, i]
				// 这样只需要计算依次比例因子
				for k = i to n+1 do
					A[j, k] = A[j, k] - A[i, k] * temp

特点

• 部分选主元法克服了前向消去法弊端
  • 最内层乘法（加法）执行次数为 $\frac {n(n-1)(2n+5) 6 \approx \frac n^3 3 \in \Theta(n^3)$
  • 始终能保证比例因子绝对值不大于1

反向替换法

在得到上三角系数矩阵中

• 从最后一个方程中可以立刻求出$x_n$
• 将$xn$带入倒数第二个方程求出$x{n-1}$
• 逐次递推得到所以解

特点

• 算法时间效率$\in \Theta(n^2)$

高斯消去法应用

• 矩阵（可逆矩阵）中应用
  • LU分解（Doolittle分解）
  • Cholesky分解（要求矩阵正定）
  • 求逆
  • 求行列式
• 高斯消元法整个算法效率取决于消去部分，是立方级
  • 事实上此方法在计算机上求解大规模方程组很难，因为舍入 误差在计算过程中会不断累积

非线性方程求解

• 5次及以上多项式没有只包含多项式系数、算术操作、开根号 的通用求根公式

• 方程的代数解并不具有很大的意义，充其量只是为方程的根设置 一个符号，然后再说方程有一个根等于这个符号（高斯）

平分法

基于连续函数界值定理，类似于连续版折半查找

算法

在区间[a, b]的端点上，$f(x)$符号取反

• 计算$f(x{mid}), x{mid}= \frac {a+b} 2$的值
• 若$f(x_{mid})=0$，则求得一个
• 否则选择使得$f(x)$能在端点上取得相反值区间$[a, x{mid}$ 、$[x{mid}, b]$
• 当包含根得区间小于预定义得$\epsilon > 0$时，就可以停止 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Bisection(f(x), a, b, eps, N)
	// 评分法求f(x) = 0的一个根
	// 输入：f(a)f(b) < 0，eps绝对误差上界，N迭代次数上界
	// 输出：(a, b)上的一个根近似（精确）值，或包含根的区间
	n = 1
		// 迭代计数
	while n <= N do
		x = (a + b)/2
		if x - a < eps
			 return x
		fval = f(x)
		if fval = 0
			return x
		if fval*f(a) < 0:
			b = x
		else
			a = x
		n += 1
	return a, b
		// 达到迭代限制，返回包含根的区间

特点

• 求解精度
  • 理论上迭代次数足够$x_n$可以任意接近真实根$x^{*}$
  • 实际上，机器使用0表示非常小的值，$\epsilon$小于特定 机器阈值时，算法不会停止，也无法得到满足条件的解
  • d对目标函数求值时可能会发生舍入误差
• 缺点
  • 相较于其他已经算法，收敛速度较慢
  • 并且无法扩展到更加一般的方程、方程组领域
• 优点
  • 区间特性容易检验

Method of False Position

试位法：类似于连续版差值查找

算法

• 类似平分法每次也使用某个区间$[a_n, b_n]$括住连续函数的 根，函数在端点取值符号相反

• 使用穿过$(a_n, f(a_n)), (b_n, f(b_n))$的直线在x轴截距 $x=\frac {a_nf(b_n) - b_nf(a_n)} {f(b_n) - f(a_n)}$作为 分割点

特点

• 对许多实例，试位法收敛速度较平分法更快

牛顿法

Newton-Raphon Method

算法

• 方法产生近似解序列：函数切线在x轴截距 $x_{n+1} = x_n - \frac {f(x_n)} {f^{‘}(x_n)},n=0,1,\cdots$

特点

• 大多数情况下，若初值$x_0$足够接近根，牛顿法能够保证序列 收敛与根；对远离根的初值，无法保证一定会收敛

• 优点

  • 牛顿法相较于平分法、试位法收敛速度更快，选定合适的 初值能够快速收敛
  • 能够应用于更一般类型的方程、方程组

• 方法每次都迭代需要重新求函数、导数值

  • 导数值等于0，则牛顿法失效
  • 导数绝对值越大，牛顿法越有效

• 牛顿法不会把根括起来