Posted 2019-07-13Updated 2021-07-16ML Model / Linear Model38 minutes read (About 5636 words)

Support Vector Machine

总述

支持向量机是二分类模型

学习要素

基本模型：定义在特征空间上的间隔最大线性分类器
学习策略：间隔最大化
- 可形式化为求解凸二次规划问题，也等价于正则化的合页损失函数最小化问题
- 间隔最大使其有别于感知机，训练数据线性可分时分离超平面唯一
  - 误分类最小策略（0-1损失）得到分离超平面的解无穷多个
  - 距离和最小策略（平方损失）得到分离超平面唯一，但与此不同
学习算法：求解凸二次规划的最优化算法

数据

在给定特征空间上的训练数据集 $T={(x_1,y_1), (x_2,y_2),\cdots,(x_N,y_N)}$，其中 $x_i \in \mathcal{X} = R^n, y_i \in {-1, +1}, i=1,2,…,N$

输入空间：欧氏空间或离散集合

特征空间：希尔伯特空间

输出空间：离散集合

SVM假设输入空间、特征空间为两个不同空间，SVM在特征空间上进行学习
线性（可分）支持向量机假设两个空间元素一一对应，并将输入空间中的输入映射为特征空间中特征向量
非线性支持向量机利用，输入空间到特征空间的非线性映射（核函数）将输入映射为特征向量

概念

Linear Support Vector Machine in Linearly Separable Case

线性可分支持向量机：硬间隔支持向量机，训练数据线性可分时，通过硬间隔最大化策略学习

直观含义：不仅将正负实例分开，而且对于最难分的实例点（离超平面最近的点），也有足够大的确信度将其分开，这样的超平面对新实例预测能力较好

Hard-margin Maximization：硬间隔最大化，最大化超平面 $(w,b)$关于线性可分训练数据集的两类样本集几何间隔

原始问题策略

约束最优化问题表述
$\begin{align} \max_{w,b} & \gamma & \\ s.t. & \frac {y_i} {\|w\|} (wx + b) \geq \gamma, i=1,2,\cdots,N \end{align}$
考虑函数间隔、几何间隔关系得到问题
- 目标、约束中使用函数间隔表示几何间隔
- 就是普通等比缩放、分母移位，不用考虑太多
而函数间隔$\hat{\gamma}$大小会随着超平面参数变化成比例变化，其取值对问题求解无影响，所以可取 $\hat{\gamma}=1$带入，得到最优化问题
- $\max \frac 1 {|w|}$和 $\min \frac 1 2 {|w|}^2$等价
- 这里确实没有通用变换技巧，因为这里的$\hat \gamma$ 是特殊的值，其取值与$w,b$相关，这是问题自然蕴含 ，可以视为还有以下一个依赖
- 当然也可以直接证明两个问题等价：先证明最优解在等式成立时取到，然后目标函数中1替换为等式左边

最大间隔分离平面存在性

若训练数据集T线性可分，则可将训练数据集中样本点完全正确分开的最大间隔分离超平面存在且唯一

存在性

训练数据集线性可分，所以以上中最优化问题一定存在可行解
又目标函数又下界，则最优化问题必有解
todo
又训练数据集中正、负类点都有，所以$(0,b)$必不是最优化可行解

唯一性

若以上最优化问题存在两个最优解$(w_1^{},b_1^{})$、 $w_2^{},b_2^{}$
显然$|w_1^{}| = |w_2^{}| = c$， $(w=\frac {w_1^{}+w_2^{}} 2,b=\frac {b_1^{}+b_2^{}} 2)$ 使最优化问题的一个可行解，则有
$c \leq \|w\| \leq \frac 1 2 \|w_1^{*}\| + \frac 1 2 \|w_2^{*} = c$
则有$|w|=\frac 1 2 |w_1^{}|+\frac 1 2 |w_2^{}|$ ，有$w_1^{} = \lambda w_2^{}, |\lambda|=1$
- $\lambda = -1$，不是可行解，矛盾
- $\lambda = 1$，则$w_1^{()} = w_2^{}$，两个最优解写为$(w^{}, b_1^{})$、$(w^{}, b_2^{})$
设$x_1^{+}, x_1^{-}, x_2^{+}, x_2^{-}$分别为对应以上两组超平面，使得约束取等号、正/负类别的样本点，则有
$\begin{align*} b_1^{*} & = -\frac 1 2 (w^{*} x_1^{+} + w^{*} x_1^{-}) \\ b_2^{*} & = -\frac 1 2 (w^{*} x_2^{+} + w^{*} x_2^{-}) \\ \end{align*}$
则有
$b_1^{*} - b_2^{*} = -\frac 1 2 [w^{*}(x_1^{+} - x_2^{+}) + w^{*} (x_1^{-} - x_2^{-})]$
又因为以上支持向量的性质可得
$\begin{align*} w^{*}x_2^{+} + b_1^{*} & \geq 1 = w^{*}x_1^{+} + b_1^{*} \\ w^{*}x_1^{+} + b_2^{*} & \geq 1 = w^{*}x_2^{+} + b_2^{*} \end{align*}$
则有$w^{}(x_1^{+} - x_2^{+})=0$，同理有 $w^{}(x_1^{-} - x_2^{-})=0$
则$b_1^{} - b_2^{} = 0$

概念

Support Vector

支持向量：训练数据集中与超平面距离最近的样本点实例

在线性可分支持向量机中即为使得约束条件取等号成立的点
在决定分离超平面时，只有支持向量起作用，其他实例点不起作用
支持向量一般很少，所以支持向量机由很少的“重要”训练样本决定

间隔边界

间隔边界：超平面$wx + b = +/-1$

支持向量位于其上
两个间隔边界之间距离称为间隔$=\frac 2 {|w|}$

算法

输入：线性可分训练数据集T

输出：最大间隔分离超平面、分类决策函数

构造并求解约束最优化问题
$\begin{align*} \min_{w,b} & \frac 1 2 {\|w\|}^2 \\ s.t. & y_i(wx_i + b) - 1 \geq 0, i=1,2,\cdots,N \end{align*}$
得到最优解$w^{}, b^{}$
得到分离超平面
$w^{*}x + b^{*} = 0$
分类决策函数
$f(x) = sign(w^{*}x + b^{*})$

多分类

1 vs n-1：对类$k=1,…,n$分别训练当前类对剩余类分类器
- 分类器数据量有偏，可以在负类样本中进行抽样
- 训练n个分类器
1 vs 1：对$k=1,…,n$类别两两训练分类器，预测时取各分类器投票多数
- 需要训练$\frac {n(n-1)} 2$给分类器
DAG：对$k=1,…,n$类别两两训练分类器，根据预先设计的、可以使用DAG表示的分类器预测顺序依次预测
- 即排除法排除较为不可能类别
- 一旦某次预测失误，之后分类器无法弥补
  - 但是错误率可控
  - 设计DAG时可以每次选择相差最大的类别优先判别

Dual Algorithm

对偶算法：求解对偶问题得到原始问题的最优解

对偶问题往往更容易求解
自然引入核函数，进而推广到非线性分类问题

对偶问题策略

Lagrange函数如下
- $\alpha_i > 0$：Lagrange multiplier
根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题
$\max_{\alpha} \min_{w,b} L(w,b,\alpha)$

求$\min_{w,b} L(w,b,\alpha)$，对拉格朗日函数求偏导置0
$\begin{align*} \triangledown_w L(w,b,\alpha) & = w - \sum_{i=1}^N \alpha_i y_i x_i = 0 \\ \triangledown_b L(w,b,\alpha) & = -\sum_{i=1}^N \alpha_i y_i = 0 \end{align*}$
解得
$\begin{align*} w = \sum_{i=1}^N \alpha_i y_i x_i \\ \sum_{i=1}^N \alpha_i y_i = 0 \end{align*}$
将以上结果代理拉格朗日函数可得
$\begin{align*} L(w,b,\alpha) & = \frac 1 2 \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i x_j) - \sum_{i=1}^N \alpha_i y_i ((\sum_{j=1}^N \alpha_j y_j x_j)x_i + b) + \sum_{i=1}^N \alpha_i \\ & = -\frac 1 2 \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_i (x_i x_j) + \sum_{i=1}^N \alpha_i \end{align*}$
以上函数对$\alpha$极大即为对偶问题，为方便改成极小
$\begin{align*} \min_{\alpha} & \frac 1 2 \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i x_j) - \sum_{i=1}^N \alpha_i \\ s.t. & \sum_{i=1}^N \alpha_i y_i = 0, \\ & \alpha_i > 0, i = 1,2,\cdots,N \end{align*}$

原始问题解

设$\alpha^{} = (\alpha_1^{}, \cdots, \alpha_N^{})$是上述对偶优化问题的解，则存在$j \in [1, N]$使得 $\alpha_j^{} > 0$，且原始最优化问题解如下 $\begin{align*} w^{*} & = \sum_{i=1}^N \alpha_i^{*} y_i x_i \\ b^{*} & = y_j - \sum_{i=1}^N \alpha_i^{*} y_i (x_i x_j) \end{align*}$

由KKT条件成立有
$\begin{align*} & \triangledown_w L(w^{*}, b^{*}, \alpha^{*}) = w^{*} - \sum_{i=1}^N \alpha_i{*} y_i x_i = 0 \\ & \triangledown_b L(w^{*}, b^{*}, \alpha^{*}) = -\sum_{i=1}^N \alpha_i^{*} y_i = 0 \\ & \alpha^{*}(y_i (w^{*} x_i + b^{*}) - 1) = 0, i = 1,2,\cdots,N \\ & y_i(w^{*} x_i + b) - 1 \geq 0, i = 1,2,\cdots,N \\ & \alpha_i^{*} \geq 0, i = 1,2,\cdots,N \\ \end{align*}$
可得
$w^{*} = \sum_i \alpha_i^{*} y_i x_i$
其中至少有一个$\alpha_j > 0$，否则$w^{*}=0$不是原问题解，且有
$\begin{align*} y_j(w^{*} x_j + b^{*}) - 1 = 0 \end{align*}$
注意到$y_j \in {-1, +1}$，则有
$b^{*} = y_j - \sum_{i=1}^N \alpha_i^{*} y_i (x_i x_j)$

分离超平面

则分离超平面为
$\sum_{i=1}^N \alpha_i^{*} y_i (x x_i) + b^{*} = 0$
分类决策函数为
$f(x) = sgn(\sum_{i=1}^N \alpha_i^{*} y_i (x x_i) + b^{*})$
即分类决策函数只依赖输入$x$和训练样本的内积

支持向量

将对偶最优化问题中，训练数据集中对应$\alpha_i^{*} > 0$ 的样本点$(x_i, y_i)$称为支持向量

由KKT互补条件可知，对应$\alpha_i^{*} > 0$的实例$x_i$有 $y_i(w^{*} x_i + b^{*}) - 1 = 0$ 即$(x_i, y_i)$在间隔边界上，同原始问题中支持向量定义一致

算法

输入：线性可分数据集$T$

输出：分离超平面、分类决策函数

构造并求解以上对偶约束最优化问题，求得最优解 $\alpha^{} = (\alpha_1^{},…,\alpha_N^{*})^T$
依据以上公式求$w^{}$，选取$\alpha^{}$正分量 $\alpha_j^{} > 0$计算$b^{}$
求出分类超平面、分类决策函数

Linear Support Vector Machine

线性支持向量机：训练数据线性不可分时，通过软间隔最大化策略学习

训练集线性不可分通常是由于存在一些outlier
- 这些特异点不能满足函数间隔大于等于1的约束条件
- 将这些特异点除去后，剩下大部分样本点组成的集合是线性可分的
对每个样本点$(x_i,y_i)$引入松弛变量$\xi_i \geq 0$
- 使得函数间隔加上松弛变量大于等于1
- 对每个松弛变量$\xi_i$，支付一个代价$\xi_i$

soft-margin maximization：软间隔最大化，最大化样本点几何间隔时，尽量减少误分类点数量

策略

线性不可分的线性支持向量机的学习变成如下凸二次规划，即软间隔最大化

$\begin{align*} \min_{w,b,\xi} & \frac 1 2 \|w\|^2 + C \sum_{i=1}^N \xi_i \\ s.t. & y_i(w x_i + b) \geq 1 - \xi_i, i=1,2,\cdots,N \\ & \xi_i \geq 0, i=1,2,\cdots,N \end{align*}$

$\xi_i$：松弛变量

$C > 0$：惩罚参数，由应用问题决定，C越大对误分类惩罚越大

最小化目标函数包含两层含义
- $\frac 1 2 |w|^2$尽量小，间隔尽量大
- 误分类点个数尽量小
以上问题是凸二次规划问题，所以$(w,b,\xi)$的解是存在的
- $w$解唯一
- $b$解可能不唯一，存在一个区间

对给定的线性不可分训练数据集，通过求解以上凸二次规划问题得到的分类超平面 $w^{*} x + b^{*} = 0$ 以及相应的分类决策函数 $f(x) = sgn(w^{*} x + b^{*})$ 称为线性支持向量机

线性支持向量包括线性可分支持向量机
现实中训练数据集往往线性不可分，线性支持向量机适用性更广

对偶问题策略

原始问题的对偶问题

$\begin{align*} \min_\alpha & \frac 1 2 \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i x_j) - \sum_{i=1}^N \alpha_i \\ s.t. & \sum_{i=1}^N \alpha_i y_i = 0 \\ & 0 \leq \alpha_i \leq C, i=1,2,\cdots,N \end{align*}$

类似线性可分支持向量机利用Lagrange对偶即可得

原始问题解

设$\alpha^{} = (\alpha_1^{}, \cdots, \alpha_N^{})$是上述对偶优化问题的解，则存在$j \in [1, N]$使得 $0 < \alpha_j^{} < C$，且原始最优化问题解如下 $\begin{align*} w^{*} & = \sum_{i=1}^N \alpha_i^{*} y_i x_i \\ b^{*} & = y_j - \sum_{i=1}^N \alpha_i^{*} y_i (x_i x_j) \end{align*}$

类似线性可分支持向量机利用KKT条件即可得

分离超平面

则分离超平面为
$\sum_{i=1}^N \alpha_i^{*} y_i (x x_i) + b^{*} = 0$
分类决策函数/线性支持向量机对偶形式
$f(x) = sgn(\sum_{i=1}^N \alpha_i^{*} y_i (x x_i) + b^{*})$
即分类决策函数只依赖输入$x$和训练样本的内积

支持向量

将对偶最优化问题中，训练数据集中对应$\alpha_i^{*} > 0$ 的样本点$x_i$称为（软间隔）支持向量

$\alpha_i^{*} < C$：则$\xi_i = 0$，恰好落在间隔边界上
$\alpha_i^{*} = C, 0 < \xi_i < 1$：间隔边界与分离超平面之间
$\alpha_i^{*} = C, \xi=1$：分离超平面上
$\alpha_i^{*} = C, \xi>1$：分离超平面误分一侧

Hinge Loss

线性支持向量机策略还可以视为最小化以下目标函数

$\sum_{i=1}^N [1-y_i(w x_i + b)]_{+} + \lambda \|w\|^2$

第一项：经验风险，合页损失函数

第二项：正则化项

$w$模越大，间隔越小，合页损失越小，所以用这个作为正则化项是合理的

参见data_science/loss

等价证明

令

$\xi_i = [1 - y_i(w x_i + b)]_{+}$

则有$\xi_i \geq 0$
且
$\left \{ \begin{align*} & y_i(w x_i + b) = 1 - \xi_i, & y_i(w x_i + b) \leq 1 \\ & y_i(w x_i + b) > 1 - \xi_i = 1, & y_i(w x_i + b) > 1 \end{align*} \right.$
所以有
$y_i(w x_i + b) \geq 1 - \xi_i$
则原问题两个约束条件均得到满足，此问题可写成
$\min_{w,b} \sum_{i=1}^N \xi_i + \lambda \|w\|^2$
取$\lambda = \frac 1 {2C}$，即同原问题

Non-Linear Support Vector Machine

非线性支持向量机

非线性问题：通过非线性模型才能很好进行分类的问题
- 通过非线性变换$\phi(x)$，将输入空间映射到特征空间（维数可能非常高）
- 原空间中非线性可分问题在特征空间可能变得线性可分，在特征空间中学习分类模型
SVM求解非线性问题时
- kernel trick：通过非线性变换将输入空间对应一个特征空间，使得输入空间中超曲面对应于特征空间的超平面模型
- 软间隔最大化策略：在特征空间中求解线性支持向量机

Kernal Trick

核技巧：线性SVM的对偶问题中，目标函数、决策函数均只涉及输入实例、实例之间的内积

将内积使用核函数代替，等价进行复杂的非线性变换
映射函数是非线性函数时，学习的含有核函数的支持向量机是非线性模型
- 学习是隐式地在特征空间中进行的，不需要显式定义特征空间、映射函数

参见data_science/ref/functions

对偶问题目标函数

$W(\alpha) = \frac 1 2 \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j K(x_i, x_j) - \sum_{i=1}^N \alpha_i$

原始问题解

分类决策函数

$\begin{align*} f(x) & = sgn(\sum_{i=1}^{N_s} \alpha_i^{*} y_i \phi(x_i) \phi(x) + b^{*}) \\ & = sgn(\sum_{i=1}^{N_s} \alpha_i^{*} y_i K(x_i, x) + b^{*}) \end{align*}$

算法

输入：训练数据集$T$

输出：分类决策函数

选取适当的核函数$K(x,z)$、适当参数C，构造求解最优化问题
$\begin{align*} \min_\alpha & \frac 1 2 \sum_{i=1}^N \sum_{j=1}^N \alpha_1 \alpha_j y_i y_j K(x_i, x_j) - \sum_{i=1}^N \alpha_i \\ s.t. & \sum_{i=1}^N \alpha_i y_i = 0 \\ & 0 \leq \alpha_i \leq C, i=1,2,...,N \end{align*}$
求得最优解 $\alpha^{} = (\alpha_1^{},\alpha_2^{},\cdots,\alpha_N^{})$
选择$\alpha^{}$的一个正分量$0 < \alpha_j^{} < C$，计算
$b^{*} = y_j - \sum_{i=1}^N \alpha_i^{*} y_i K(x_i x_j)$
构造决策函数

$K(x,z)$是正定核函数时，最优化问题是凸二次规划，有解

Sequential Minimal Optimization

序列最小最优化算法，主要解如下凸二次规划的对偶问题

$\begin{align*} \min_\alpha & \frac 1 2 \sum_{i=1}^N \sum_{j=1}^N \alpha_1 \alpha_j y_i y_j K(x_i, x_j) - \sum_{i=1}^N \alpha_i \\ s.t. & \sum_{i=1}^N \alpha_i y_i = 0 \\ & 0 \leq \alpha_i \leq C, i=1,2,...,N \end{align*}$

凸二次规划有很多算法可以求得全局最优解，但是在训练样本容量较大时，算法会很低效

思想

将原问题不断分解为子问题求解，进而求解原问题

如果所有变量的解都满足此优化问题的KKT条件，得到此最优化问题的一个可能解
- 对凸二次规划就是最优解，因为凸二次规划只有一个稳定点
否则选择两个变量，固定其他变量，构建一个二次规划
- 目标是使得解符合KKT条件，但是因为等式约束的存在，不可能单独改变一个变量而保持等式约束
- 子问题有解析解，求解速度快
- 二次规划问题关于两个变量的解会使得原始二次规划的目标函数值变得更小，更接近原始二次规划的解（这里SMO原始论文有证明，违反KKT条件的变量可以做到）
不失一般性，假设选择两个变量$\alpha_1, \alpha_2$，其他变量$\alpha_i(i=3,4,…,N)$是固定的，则SMO最优化子问题
- $K_{ij} = K(x_i, x_j), i,j=1,2,\cdots,N$
- $\zeta$：常数

两变量二次规划取值范围

由等式约束，$\alpha_1, \alpha_2$中仅一个自由变量，不妨设为$\alpha_2$
- 设初始可行解为$\alpha_1, \alpha_2$
- 设最优解为$\alpha_1^{}, \alpha_2^{}$
- 未经剪辑（不考虑约束条件而来得取值范围）最优解为 $\alpha_2^{**}$
由不等式约束，可以得到$\alpha_2$取值范围$[L, H]$
- $y_1 = y_2 = +/-1$时
  $\begin{align*} H & = \min \{C, \alpha_1 + \alpha_2 \} \\ L & = \max \{0, \alpha_2 + \alpha_1 - C \} \end{align*}$
- $y_1 \neq y_2$时
  $\begin{align*} L & = \max \{0, \alpha_2 - \alpha_1 \} \\ L & = \min \{C, C + \alpha_2 - \alpha_1 \} \end{align*}$
- 以上取值范围第二项都是应用等式约束情况下，考虑不等式约束

两变量二次规划求解

为叙述，记

$\begin{align*} g(x) & = \sum_{i=1}^N \alpha_i y_i K(x_i, x) + b \\ E_j & = g(x_j) - y_j \\ & = (\sum_{i=1}^N \alpha_i y_i K(x_i, x_j)) - y_j \end{align*}$

$g(x)$：SVM预测函数（比分类器少了符号函数）（函数间隔）
$E_j$：SVM对样本预测与真实值偏差

以上两变量二次规划问题，沿约束方向未经剪辑解是 $\begin{align*} \alpha_2^{**} & = \alpha_2 + \frac {y_2 (E_1 - E_2)} \eta \\ \eta & = K_{11} + K_{22} - 2K_{12} \\ & = \|\phi(x_1) - \phi_(x_2)\|^2 \end{align*}$ 剪辑后的最优解是 $\begin{align*} \alpha_2^{*} & = \left \{ \begin{array}{l} H, & \alpha_2^{**} > H \\ \alpha_2^{**}, & L \leq \alpha_2^{**} \leq H \\ L, & \alpha_2^{*} < L \end{array} \right. \\ \alpha_1^{*} & = \alpha_1 + y_1 y_2 (\alpha_2 - \alpha_2^{*}) \end{align*}$

记
$\begin{align*} v_i & = \sum_{j=3}^N \alpha_j y_j K(x_i, x_j) \\ & = g(x_i) - \sum_{j=1}^2 \alpha_j y_j K(x_i, x_j) - b i=1,2 \end{align*}$
由等式约束$\alpha_1 = (\zeta - y_2 \alpha_2) y_1$，均带入目标函数有
$\begin{align*} W(\alpha_1, \alpha_2) = & \frac 1 2 K_{11} (\zeta - y_2 \alpha_2)^2 + \frac 1 2 K_{22} \alpha_2^2 + y_2 K_{12} (\zeta - y_2 \alpha_2) \alpha_2 - \\ & y_1 (\zeta - \alpha_2 y_2) - \alpha_2 + v_1 (\zeta - \alpha_2 y_2) + y_2 v_2 \alpha_2 \end{align*}$
对$\alpha_2$求导置0可得
$\begin{align*} (K_{11} + K_{22} - 2K_{12}) \alpha_2 & = y_2 (y_2 - y_1 + \zeta K_{11} - \zeta K_{12} + v_1 + v_2) \\ & = y_2 [y_2 - y_1 + \zeta K_{11} - \zeta K_{12} + (g(x_1) - \sum_{j=1}^2 y_j \alpha_j K_{1j} - b) - (g(x_2) - \sum_{j=1}^2 y_j \alpha_j K_{2j} -b )] \end{align*}$
带入$\zeta = \alpha_1 y_1 + \alpha_2 y2$，可得
$\begin{align*} (K_11 + K_22 - 2K_{12}) \alpha_2^{**} & = y_2((K_{11} + K_{22} - 2K_{12}) \alpha_2 y_2 + y_2 - y_1 + g(x_1) - g(x_1)) \\ & = (K_11 + K_{22} - 2K_{12}) \alpha_2 + y_2 (E_1 - E_2) \end{align*}$

变量选择

SMO算法每个子问题的两个优化变量，其中至少一个违反KKT条件

外层循环—首个变量选择

在训练样本中选择违反KKT条件最严重的样本点，将对应的变量作为第一个变量$\alpha_1$

检查样本点是否满足KKT条件
$\begin{align*} \alpha_i = 0 \Leftrightarrow y_i g(x_i) \geq 1 \\ 0 < \alpha_i < C \Leftrightarrow y_i g(x_i) = 1 \\ \alpha_i = C \Leftrightarrow y_i g(x_i) \leq 1 \end{align*}$
检验过程中
- 首先遍历所有满足条件的$0 < \alpha_i < C$样本点，即在间隔边界上的支持向量点
- 若没有找到违背KKT条件的样本点，则遍历整个训练集

内层循环

第二个变量$\alpha_2$选择标准是其自身有足够大的变化，以加快计算速度

由以上推导知，$\alpha_2^{*}$取值依赖于$|E_1 - E_2|$，所以可以选择$\alpha_2$使其对应的$|E_1 - E_2|$最大
- $\alpha_1$已经确定，$E_1$已经确定
- $E_1 > 0$：选最小的$E_2$
- $E_1 < 0$：选最大的$E_2$
但以上方法可能不能使得目标函数值有足够下降，采用以下 启发式规则继续选择$\alpha_2$
- 遍历间隔边界上的点
- 遍历整个训练数据集
- 放弃$\alpha_1$

更新阈值

$0< \alpha_1^{*} < C$时，由KKT条件可知
- 则有
  $b_1^{*} = y_1 - \sum_{i=3}^N \alpha_i y_i K_{i1} - \alpha_1^{*} y_1 K_{11} - \alpha_2^{*} y_2 K_{21}$
- 将$E_1$定义式带入有
  $b_1^{*} = -E_1 - y_1 K_{11} (\alpha_1^{*} - \alpha_1) - y_2 K_{21} (\alpha_2^{*} - \alpha_2) + b$
类似的$0 < \alpha_2^{*} < C$时
$b_2^{*} = -E_2 - y_2 K_{22} (\alpha_2^{*} - \alpha_2) - y_1 K_{12} (\alpha_1^{*} - \alpha_1) + b$
若
- $0 < \alpha_1^{}, \alpha_2^{} < C$，则 $b_1{} = b_2^{}$
- $\alpha_1^{}, $\alpha_2^{}$均为0、C，则 $[b_1^{}, b_2^{}]$中均为符合KKT条件的阈值，选择中点作为新阈值$b^{*}$
同时使用新阈值更新所有的$E_i$值
- $S$：所有支持向量的集合

算法

输入：训练数据集$T$，精度$\epsilon$

输出：近似解$\hat \alpha$

初值$\alpha^{(0)}$，置k=0
选取优化变量$\alpha_1^{(k)}, \alpha_2^{(k)}$，解析求解两变量最优化问题得$\alpha_1^{(k+1)}, \alpha_2^{(k+2)}$，更新$\alpha^{(k+1)}$
若在精度范围内满足停机条件（KKT条件）
$\begin{align*} & \sum_{i=1}^N \alpha_i y_i = 0 \\ & 0 \leq \alpha_i \leq C, i=1,2,\cdots,N \\ & y_i g(x_i) = \left \{ \begin{array}{l} \geq 1, & \{x_i | \alpha_i = 0\} \\ = 1, & \{x_i | 0 < \alpha_i < C\} \\ \leq 1, & \{x_i | \alpha_i = C\} \end{array} \right. \\ & g(x_i) = \sum_{j=1}^N \alpha_j y_j K(x_j, x_i) + b \end{align*}$
则转4，否则置k=k+1，转2
取$\hat \alpha = \alpha^{(k+1)}$

Posted 2019-07-13Updated 2021-07-16ML Specification / Computer Vision4 minutes read (About 540 words)

Local Binary Pattern

综述

局部二值模式：描述图像局部纹理的特征算子

具有旋转不变性、灰度不变性
通过对窗口中心的、领域点关系进行比较，重新编码形成新特征以消除外界场景对图像影响，一定程度上解决了复杂场景下（光照变换）特征描述问题
分类
- 经典LBP：3 * 3正方向窗口
- 圆形LBP：任意圆形领域

Classical LBP

Sobel Operator

Laplace Operator

Canny Edge Detector

Circular LBP

缩略图Hash

对图像进行特征提取得到0、1特征向量
通过比较图片向量特征间汉明距离即可计算图片之间相似度

Average Hashing

aHash：平均哈希算法

将原始图片转换为64维0、1向量，即提取出的特征

步骤

缩放图片：将图像缩放到8 * 8=64像素
- 保留结构、去掉细节
- 去除大小、纵横比差异
灰度化：把缩放后图转换为256阶灰度图
计算平均值：计算灰度图像素点平均值
二值化：遍历64个像素点，大于平均值者记为1、否则为0

Perceptual Hashing

pHash：感知哈希算法

利用离散余弦变换降低频率，去除成分较少的高频特征
特点
- 相较于aHash更稳定

步骤

缩放图片：将图片缩放至32 * 32
灰度化：将缩放后图片转换为256阶灰度图
计算DCT：把图片分离成频率集合
缩小DCT：保留32 32左上角8 8代表图片最低频率
计算平均值：计算缩小DCT均值
二值化：遍历64个点，大于平均值者记为1、否则为0

Differential Hashing

dHash：差异哈希算法

基于渐变实现
特点
- 相较于dHash非常快
- 相较于aHash效果好

步骤

缩放图片：将图片缩放至9 * 8
灰度化：将缩放后图片转换为256阶灰度图
计算差异值：对每行像素计算和左侧像素点差异，得到8 * 8
二值化：遍历64个点，大于0记为1、否则为0

Posted 2019-07-13Updated 2021-07-16ML Specification / Computer Vision13 minutes read (About 1986 words)

传统图像特征提取

Scale-Invariant Feature Transform

SIFT：通过求图中interest/corner point、及其scale和 orientation描述子得到特征，并进行图像特征点匹配

SIFT是检测局部特征的算法
- 实质：在不同尺度空间查找关键点，计算关键点大小、方向、尺度信息，进而组成对关键点得描述
- SIFT查找的关键点为突出、稳定的特征点，不会因光照、仿射变换、噪声等因素而改变
  - 角点
  - 边缘点
  - 暗区亮点
  - 亮区暗点
- 匹配过程就是对比特征点过程

优点
- 稳定性：具有旋转、尺度、平移、视角、亮度不变性，利于对目标特征信息进行有效表达
- 独特性：信息量丰富，适合海量特征数据中进行匹配
- 多量性：少数物体也可以产生大量SIFT特征向量
- 可扩展性：可以方便同其它形式特征向量联合
- 对参数调整稳健性好：可以根据场景调整特征点数量进行特征描述、方便特征分析
缺点
- 不借助硬件加速、专门图像处理器难以实现

构建尺度空间

图像的尺度空间：解决如何对图像在所有尺度下描述的问题

思想：对原始图像进行尺度变换，获得多尺度空间下图像表示序列，模拟图像数据的多尺度特征
- 对序列进行尺度空间主轮的提取
- 以主轮廓作为特征向量，实现边缘、角点检测、不同分辨率上稳定关键点提取
对高斯金字塔生成的O组、L层不同尺度图像，$(O, L)$就构成高斯金字塔的尺度空间
- 即以高斯金字塔组$O$、层$L$作为坐标
- 给定一对$(o,l)$即可唯一确定一幅图像

image_scale_space

图像金字塔

图像金字塔：以多分辨率解释图像的结构

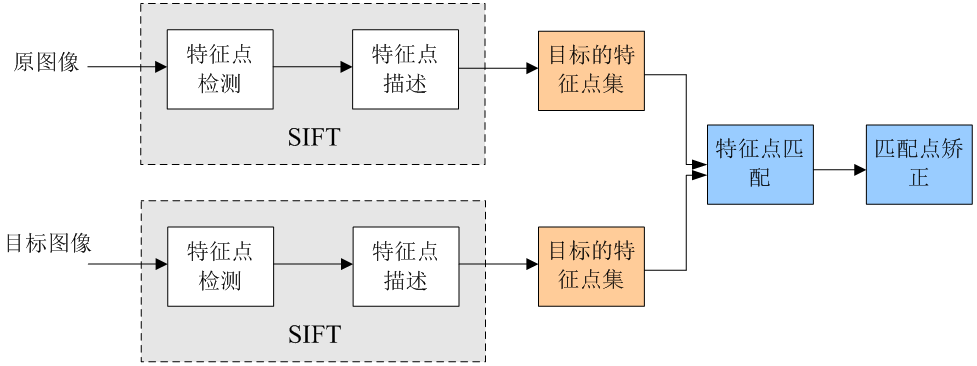
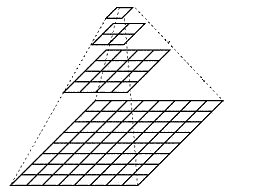
image_pyramid

通过对原始图像进行多尺度像素采样方式生成N个不同分辨率的图像
- 图像分辨率从下至上逐渐减小
- 直至金字塔顶部只包含一个像素
获取图像金字塔步骤
- 利用低通滤波器平滑图像
- 对平滑图像进行采样
  - 上采样：分辨率逐渐升高
  - 下采样：分辨率逐渐降低

高斯金字塔

高斯金字塔：由很多组图像金字塔构成，每组金字塔包含若干层

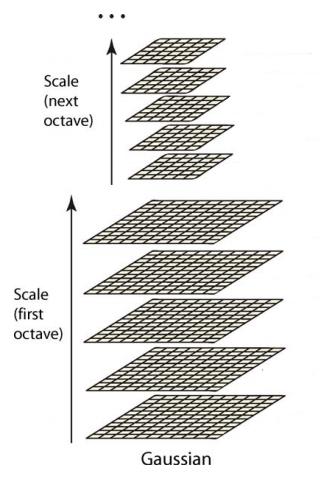
image_gaussian_pyramid

同一组金字塔中
- 每层图像尺寸相同
- 仅高斯平滑系数$\sigma$不同，后一层图像是前一层$k$倍
不同组金字塔中
- 后一组图像第一个图像是前一组倒数第三个图像二分之一采样
- 图像大小是前一组一半

构建过程

构建第1组图像金字塔
- 第1层：将原图扩大一倍得到
- 第2层：第1层图像经过高斯卷积得到
  - SIFT算子中，高斯平滑参数$\sigma=1.6$
- 第k层：
  - $\sigma$乘以比例系数得到新平滑因子 $\sigma = k\sigma$，
  - 使用平滑因子平滑第k层图像得到
- 不断重复得到L层图像
构建第k组图像金字塔
- 第1层：将第k-1组金字塔倒数第3层做比例因子为2的降采样得到
- 之后同第1组图像金字塔
不断重复得到O组图像金字塔，共计O * L个图像

Difference of Gaussian

DOG金字塔：差分金字塔

image_dog_pyramid

DOG金字塔第0组第k层由高斯金字塔第0组第k+1层减去第k层得到
- DOG金字塔每组比高斯金字塔少一层
- 按高斯金字塔逐组生成$O * (L-1)$个差分图像
DOG图像包含大量信息（需要归一化才能人眼可见）
- 在不同DOG层（即不同模糊程度、不同尺度）都存在的特征即SIFT要提取的稳定特征
- 后续SIFT特征点都是在DOG金字塔中进行

image_dog_pyramid_instance

空间极值点检测

空间极值点检测：关键点初步查探

寻找DOG图像极值点：每个像素点和其所有相邻点比较
- 需要同时比较图像域、尺度空间域相邻点
- 保证关键点在尺度空间、二维图像空间上都是局部极值点
对二维图像空间，对中心点
- 图像域：与3 * 3领域内8个点比较
- 同组尺度空间：和上下两层图像中2 * 9个点比较
极值点是在不同尺度空间下提取的，保证了关键点尺度不变性

精确定位

稳定关键点精确定位

DOG值对噪声、边缘敏感，需要对局部极值进一步筛选，去除不稳定、错误检测极值点
构建高斯金字塔时采用下采样图像，需要求出下采样图像中极值点对应在原始图像中确切位置

方向信息分配

稳定关键点方向信息分配

为关键点分配方向信息赋予关键点旋转不变性
通过对稳定关键点求梯度实现方向分配

计算方式

梯度幅度值
$m(x, y) = \sqrt {(L(x+1,y) - L(x-1,y))^2 + (L(x,y+1) - L(x,y-1))^2}$
梯度方向
$\theta(x,y) = tan^{-1} (\frac {L(x,y+1) - L(x,y-1)} {L(x+1,y) - L(x-1,y)})$
通过梯度方向直方图给出关键点梯度方向
- 计算关键点为中心领域内所有点梯度方向，在0~360度范围
- 把所有梯度方向划分到36个区域，每个方向代表10度
- 累计每个方向关键点数目，生成梯度方向直方图
- 将直方图中峰值代表方向作为关键点主方向
- 若存在相当于峰值80%大小的方向，则作为辅方向
  - 辅方向可以增强匹配的鲁棒性
  - Lowe指出：大概15%关键点具有辅方向，且这些关键点对稳定匹配起关键作用

关键点描述

关键点描述：以数学方式定义关键点的过程，包括关键点周围对其有贡献的领域点

对关键点周围像素区域分块
- 计算块内梯度直方图
- 生成具有独特性的向量，作为对该区域图像信息的抽象表述
如下图
- 将关键点周围分为2 * 2块
- 对每块所有像素点梯度做高斯加权（softmax拉开差距？）
- 每块最终取8个方向，得到2 2 8维向量，作为中心关键点数学描述

Lowe实验表明：采用4 4 8共128维描述子表征关键点，综合效果最好

特征点匹配

特征点匹配：计算两组特征点128维描述向量的欧式距离

欧式距离越小、相似度越高，小于指定阈值时既可认为匹配成功

Speeded Up Robust Feature

SURF特征：对SIFT算法的改进，降低了时间复杂度，提高了稳健性

主要是简化SIFT一些运算
- 高斯二阶维分模型简化，卷积平滑操作仅需要转换为加减运算
- 最终生成特征向量维度从128维减少为64维

Brief

Oriented Brief

ORB：Brief算法改进版

比SIFT算法快100倍

Posted 2019-07-13Updated 2021-07-16ML Specification / Computer Vision4 minutes read (About 543 words)

角点检测特征提取

综述

corner point：角点，邻域各方向上灰度变化值足够高的点，是图像边缘曲线上曲率极大值的点

思想、步骤

使用角点检测算子，对图像每个像素计算 cornner response function值
- $w(x,y)$：window function，窗口函数
- $I(x,y)$：图像梯度
- $E(x,y)$：角点响应函数，体现灰度变化剧烈程度，变化程度剧烈则窗口中心就是角点
阈值化角点响应函数值
- 根据实际情况选择阈值$T$
- 小于阈值$T$者设置为0
在窗口范围内对角点响应函数值进行非极大值抑制
- 窗口内非响应函数值极大像素点置0
获取非零点作为角点

Moravec

todo

步骤

取偏移量$(\Delta x, \Delta y)$为 $(1,0), (1,1), (0,1), (-1,1)$，分别计算每个像素点灰度变化
对每个像素点(x_i, y_i)$计算角点响应函数 $R(x) = min {E}$
设定阈值$T$，小于阈值者置0
进行非极大值抑制，选择非0点作为角点检测结果

特点

二值窗口函数：角点响应函数不够光滑
只在4个方向（偏移量）上计算灰度值变化：角点响应函数会在多处都有较大响应值
对每个点只考虑响应函数值最小值：算法对边缘敏感

Harris

Good Features to Track

Feature from Accelerated Segment Test

FAST：加速分割测试获得特征

Posted 2019-07-13Updated 2021-07-16ML Specification / NLP4 minutes read (About 555 words)

NLP 总述

文本挖掘

文本处理：将非结构化数据转换为结构化数据
预测建模
- 文本分类：根据观察到的对象特征值预测其他特征值
描述建模
- 文本聚类：对数据对象进行概括，以看到数据对象的最重要特征
  - 适应范围非常广
- 聚类分析
基于相似度方法
- 需要用户显式指定相似度函数
- 聚类算法根据相似度的计算结果将相似文本分在同一个组
- 每个文本只能属于一个组，因此也成为“硬聚类”
基于模型的方法
- 文本有多个标签，也成为“软聚类”

话题检测

找出文档中的K个话题，计算每个文档对话题的覆盖率

话题表示方法

基于单个词

基于词分布

问题描述

输入

N个文档构成的文本集C

话题个数K

词典V

输出

K个话题的分布 $(\theta_1, \theta2, \cdots, \theta_K)$

N个文档在K个话题上的概率分布 $(\pi_1, \pi_2, \cdots, \pi_N)$

语言模型

词向量：将向量表示词

1-of-N representation/one hot representation：one-hot 表示词
- 词向量维度为整个词汇表大小
- 简单、效率不高
distributed representation：embedding思想，通过训练，将词映射到较短词向量中
- 词向量维度自定义
- 容易分析词之间关系

Continuous Bag-of-Words

CBOW：输入特征词上下文相关词对应词向量，输出特征词的词向量

CBOW使用词袋模型
- 特征词上下文相关从平等，不考虑和关注的词之间的距离

Skip-Gram

Skip-Gram：输入特征词词向量，输出softmax概率靠前的词向量

神经网络词向量

神经网络词向量：使用神经网络训练词向量

一般包括三层：输入层、隐层、输出softmax层
从隐藏层到输出softmax层计算量很大
- 需要计算所有词的softmax概率，再去找概率最大值

Posted 2019-07-13Updated 2021-07-16ML Specification / NLPa few seconds read (About 0 words)

RNN 语言模型

Posted 2019-07-13Updated 2021-08-02Linux / Toolan hour read (About 8004 words)

Make

Make基础

Make：根据指定的Makefile文件构建新文件

1 2	$ make [-f makefile] [<target>] # 指定使用某文件中的规则，默认`makefile`/`Makefile`

make默认寻找当前目中GNUmakefile/makefile/Makefile 文件作为配置文件
默认用makefile中首个目标文件作为最终目标文件，否则使用<target>作为目标文件

Make参数

-b/-m：忽略和其他版本make兼容性
-B/--always-make：总是更新/重编译所有目标
-C <dir>/--directory=<dir>：指定读取makefile的目录，相当于$ cd <dir> && make
- 指定多个-C <dir>，make将按次序合并为最终目录
- -C时，-w选项自动打开
--debug[=<options>]：输出make调试信息
- a：all，输出所有调试信息
- b：basic，基本信息
- v：verbose，基本信息之上
- i：implicit，所有隐含规则
- j：jobs，执行规则中命令的详细信息，如：PID、返回码
- m：makefile，make读取、更新、执行makefile的信息
-d：等价于--debug=a
-e/--environment-overrides：环境变量覆盖makefile中值
-f <file>/--file=<file>/--makefile=<file>：指定 makefile
- 可以多次传递参数-f <filename>，所有makefile合并传递给make
-h/--help：帮助
-i/--ignore-errors：忽略执行时所有错误
-I <dir>/--include-dir=<dir>：搜索includemakefile 路径
- 可以多个-I <dir>指定多个目录
-j [<jobsum>]/-jobs[=<jobsum>]：指定同时运行命令数
- 进程数
- 默认同时运行尽量多命令
- 多个-j时最后者生效
-k/--keep-going：出错不停止运行
- 若目标生成失败，依赖于其上目标不会继续执行
-l <load>/--load-average[=<load>]
--max-load[=<load>]：make命令负载
-n/--just-print/--dry-run/--recon：仅输出执行过程中命令序列，不执行
-o <file>/--old-file=<file>/--assume-old=<file>：不重新生成指定的<file>，即使目标依赖其

-p/--print-data-base：输出makefile中所有数据：规则、变量等

$ make -qp
	# 只想输出信息，不执行makefile
$ make -p -f /dev/null
	# 查看执行makefile前的预设变量、规则

-q/--question：不执行命令、不输出，仅检查指定目标是否需要更新
- 0：需要更新
- 2：有错误发生
-r/--no-builtin-rules：禁用make任何隐含规则
-R/--no-builtin-variables：禁用make任何作用于变量上的隐含规则
-s/--silent/quiet：禁止显示所有命令输出
-S/--no-keep-going/--stop：取消-k作用
-t/--touch：修改目标日期为最新，即组织生成目标的命令执行
-v/--version：版本
-w/--print-directory：输出运行makefile之前、之后信息
- 对跟踪嵌套式调用make有用
--no-print-directory：禁止-w选项
-W <file>/--what-if=<file>/--new-file=<file>/--assume-file=<file>
- 联合-n选项，输出目标更新时的运行动作
- 没有-n，修改<file>为当前时间
--warn-undefined-variables：有未定义变量是输出警告信息

步骤

读入所有makefile
读入被include其他makefile
初始化（展开）文件中变量、函数，计算条件表达式
展开模式规则%、推导隐式规则、分析所并规则
为所有目标文件创建依赖关系链
根据依赖关系，决定需要重新生成的目标
执行生成命令

Makefile基本语法

控制符号

#：注释
@：消除echoing，默认make会打印每条命令
-：忽略命令出错
通配符同bash
- *：任意字符
- ?：单个字符
- [...]：候选字符
- ~：用户目录
  - ~：当前用户目录
  - ~xxx：用户xx目录

%：模式匹配

1 2	%.o: %.c # 匹配所有c文件，目标为`.o`文件

$：引用、展开变量，执行函数

引用其他Makefile

1	include <filename>

<filename>可以是默认shell的文件模式，包含通配符、路径

include之前可以有空格，但是不能有<tab>（命令提示）

make寻找其他makefile，将其内容放当前位置
若文件没有明确指明为绝对路径、相对路径，make会在以下目录中寻找
- -I、--include-dir参数
- /usr/local/bin/include、/usr/include
make会include环境变量MAKEFILES中文件
- 不建议使用环境变量MAKEFILES，会影响所有make
文件未找到，make会生成一条警告信息，但继续载入其他文件，完成makefile读取之后，make会重试寻找文件，失败报错
- 可以使用-include/sinclude代替，忽略include过程中的任何错误

Makefile显式规则

1 2	<target>: <prerequisite> [tab]<commands>

<target>：目标

<prerequisites>：前置条件

<commands>：命令，和前置条件至少存在一个

1 2	a.txt: b.txt c.txt cat b.txt c.txt > a.txt

makefile中规则是生成目标的规则
make自顶向下寻找可以用于生成目标的规则，生成最终目标类似调用函数栈
- 前置条件/依赖类似于被调用函数
- 命令类似于函数体
- 目标类似于函数返回值

Target

目标：make的目标

目标通常是文件名，指明需要构建的对象
- 文件名可以是多个，之间使用空格分隔
不是文件名的目标称为伪目标，视为某种操作

多目标

多目标规则意义是多个目标共享规则依赖、声明命令，并 不是需要同时生成多个目标

需要多目标中的任何一个时，多目标规则就会被应用，其中命令被执行

每次只生成单独目标的多目标规则，目标之间只是单纯的可以合并简化规则中的命令

bigoutput littleoutput: text.g
	generate text.g -$(subst output,,$@) > $@

	# 等价于

bigoutput: text.g
	generate text.g -big > bigoutput
littleoutput: text.g
	generate text.g -little > littleoutput

同时生成多个目标的多目标规则，多个目标应该满足 需要同时生成、不能单独修改，否则没有必要定义为多目标，当然这其实也是合并简化规则中的命令
1
2
%.tab.c %.tab.h: %.y
bison -d $<

Phony Target

todo

伪目标：目标是某个操作的名字，每次执行都会执行命令

.PHONY: clean
	# 明确声明是*伪目标*，可省略
clean:
	rm *.o

若省略.PYHONY，要求当前目中不存在同名文件，否则make 认为目标已存在，不会执行命令

GNU规范

GNU推荐makefile中包含的伪目标、命名

all：编译所有目标
clean：删除所有被make创建的文件
install：安装已编译好程序，即将目标执行文件拷贝到指定目标中
print：列出改变过的源文件
tar：打包源程序备份
dist：创建压缩文件
tags：更新所有目标，以备完整地编译使用
check/test：测试makefile流程

静态库

目标archive(member)：指定静态库文件、及其组成

这种定义目标的方法就是方便ar命令

foolib(hack.o kludge.o): hack.o kludge.o
	ar cr foolib hack.o kludge.o

foolib(hack.o): hack.o
	ar cr foolib hack.l kudge.o
foolib(kludge.o): kludge.o
	ar cr foolib kludge.o

	# 确实等价，但是这个看起来有点不对劲，只要传了任何一个
		# 静态库的构成，就执行命令???

foolib(*.o): hack.o kludge.o
	# 这样更好???

Prerequisites

前置条件/依赖：生成目标的依赖

通常是一组空格分隔的文件名，为空则说明目标的生成和其他文件无关
指定目标是否重新构建的判断标准，只要有一个前置文件不存在、有过更新（时间戳比较），目标就需要更新
若前置文件不存在，则需要建立以其作为目标的规则用于生成， make target时会自动调用

1 2	source: file1 file2 file3 # 利用伪目标+前置条件，同时构建多个文件

Commands

命令：更新、构建文件的方法

在linux下默认使用环境变量SHELL（/bin/sh）执行命令，
在MS-DOS下没有SHELL环境变量，会在PATH环境变量中寻找，并自动加上.exe、.bat、.sh等后缀

`<tab>`

每行命令前必须有一个<tab>，否则需要使用提前声明

1
2
3

.RECIPEPREFIX=>
all:
> echo Hello, world

Shell进程

每行命令在单独的shell进程中执行，其间没有继承关系（即使是同一个规则中）

多条命令可以使用;分隔

1 2	var-kept: export foo=bar; echo "foo=[$$foo]"

可类似python\换行

1
2
3

var-kept:
	export foo=bar; \
	echo "foo=[$$foo]"

使用.ONESHELL命令

.ONESHELL
var-kept:
	export foo=bar
	echo "foo=[$$foo]"

嵌套执行Make

大工程中不同模块、功能源文件一般存放在不同目录，可以为每个目录单独建立makefile

利于维护makefile，使得其更简洁
利于分块/分段编译
最顶层、调用make执行其他makefile的makefile称为总控

subsystem:
	cd subdir && $(MAKE)
	# 等价
subsystem:
	$(MAKE) -C subdir

subsystem:
	cd subdir && $(MAKE) -w MAKEFLAGS=
	# 将命令行参数`MAKEFLAGS`置空，实现其不向下级传递
	# 指定`-w`参数输出make开始前、后信息

搜索路径

`VPATH`

VPATH：makefile中定义的特殊环境变量，指明寻找依赖文件、目标文件的路径

1	VPATH = src:../src

:分隔路径
当前目录优先级依旧最高

`vpath`

vpath：make关键字，指定不同模式文件不同搜索目录

vpath <pattern> <directories>
vpath %.h ../headers
	# 指明`<pattern>`模式文件搜索目录
vpath <pattern>
	# 清除`<pattern>`模式文件搜索目录设置
vpath
	# 清除所有`vapth`设置

<pattern>中使用%匹配0或若干字符

vpath可以重复为某个模式指定不同搜索策略，按照出现顺序先后执行搜索

隐含规则

隐含规则是一种惯例，在makefile中没有书写相关规则时自动照其运行
- 隐含规则中优先级越高的约经常被使用
- 甚至有些时候，显式指明的目标依赖都会被make忽略
  1
  2
  3
  4
  foo.o: foo.p
  # Pascal规则出现在C规则之后
  # 若当前目录下存在foo.c文件，C隐含规则生效，生成
  # foo.o，显式依赖被忽略
- 很多规则使用后缀规则定义，即使使用-r参数，其仍会生效
隐含规则会使用系统变量
- CPPFLAGS/CFLAGS：C++/C编译时参数
可以通过模式规则自定义隐含规则，更智能、清晰
- 后缀规则有更好的兼容性，但限制更多

常用隐含规则

编译C

目标：<n>.o
依赖包含：<n>.c
生成命令
1
$(CC) -c $(CPPFLAGS) $(CFLAGS)

编译CPP

目标：<n>.o
依赖包含<n>.cc/<n>.c
生成命令
1
$(CXX) -c $(CPPFLAGS) $(CFLAGS)

编译Pascal

目标：<n>.p
依赖包含：<n>.p
生成命令
1
$(PC) -c $(PFLAGS)

编译Fortran/Ratfor

目标：<n>.o
依赖包含：<n>.f/<n>.r

生成命令

$(FC) -c $(FFLAGS)
	# `.f`
$(FC) -c $(FFLAGS) $(CPPFLAGS)
	# `.F`
$(FC) -c $(FFLAGS) $(RFLAGS)
	# `.r`

预处理Fortran/Ratfor

目标：<n>.f
依赖包含：<r>.r/<n>.F

生成命令

$(FC) -F $(CPPFLAGS) $(FFLAGS)
	# `.F`
$(FC) -F $(FFLAGS) $(RFLAGS)
	# `.r`

转换Ratfor、有预处理的Fortran至标准Fortran

编译Modula-2

目标：<n>.sym/<n>.o
依赖包含：<n>.def/<n>.mod

生成命令

$(M2C) $(M2FLAGS) $(DEFFLAGS)
	# `.def`
$(M2C) $(M2FLAGS) $(MODFLAGS)
	# `.mod`

汇编汇编

目标：<n>.o
依赖包含：<n>.s
生成命令：默认使用编译器as
1
2
$(AS) $(ASFLAGS)
# `.s`

预处理

目标：<n>.s
依赖包含：<n>.S
生成命令：默认使用预处理器cpp
1
2
$(CPP) $(ASFLAGS)
# `.S`

链接object

目标：<n>
依赖包含：<n>.o
生成命令：默认使用C工具链中链接程序ld
1
$(CC) <n>.o $(LOADLIBS) $(LDLIBS)

Yacc C

目标：<n>.c
依赖包含：<n>.y
生成命令
1
$(YACC) $(YFALGS)

Lex C

目标：<n>.c
依赖包含：<n>.c
生成命令
1
$(LEX) $(LFLAGS)

Lex Ratfor

目标：<n>.r
依赖包含：<n>.l
生成命令
1
$(LEX) $(LFLAGS)

创建Lint库

目标：<n>.ln
依赖包含：<n>.c/<n>.y/<n>.l
生成命令
1
$(LINT) $(LINTFLAGS) $(CPPFLAGS) -i

创建静态链接库

目标：<archive>(member.o)
依赖包含：member
生成命令
1
ar cr <archive> member.o

即使目标传递多个memeber.o，隐含规则也只会解析出把首个 .o文件添加进静态链接库中的命令

1
2
3
4
(%.o): %.o
	$(AR) rv $@ $*.o
	# 此命令可以得到添加所有`member.o`的命令
	# 但是此时`$*=member.o member`

隐含规则使用变量

隐含规则使用的变量基本都是预先设置的变量

makefile中改变
make命令环境变量传入
设置环境变量
-R/--no-builtin-variable参数取消变量对隐含规则作用

命令

AR：函数打包程序，默认ar
AS：汇编语言编译程序，默认as
CC：C语言编译程序，默认cc
CXX：C++语言编译程序，默认c++/g++
CPP：C程序预处理器，默认$(CC) -E/cpp
FC：Fortran、Ratfor编译器、预处理程序，默认f77
PC：Pascal语言编译程序，默认pc
LEX：Lex文法分析器程序（针对C、Ratfor），默认lex
YACC：Yacc文法分析器程序（针对C、Ratfor），默认 yacc -r
GET：从SCCS文件中扩展文件程序，默认get
CO：从RCS文件中扩展文件程序，默认co
MAKEINFO：转换Texinfo .texi到Info程序，默认 makeinfo
TEX：转换TeX至Tex DVI程序，默认tex
TEXI2DVI：转换Texinfo至Tex DVI程序，默认texi2dvi
WEAVE：转换Web至TeX程序，默认weave
TANGLE：转换Web至Pascal程序，默认tangle
CTANGEL：转换C Web至C，默认ctangle
RM：删除文件命令，默认rm -f

命令参数

未指明默认值则为空

ARFLAGS：静态链接库打包程序AR参数，默认rv
ASFLAGS：汇编语言汇编器参数
CFLAGS：C编译器参数
CXXFLAGS：C++编译器参数
CPPFLAGS：C预处理参数
LDFLAGS：链接器参数
FFLAGS：Fortran编译器参数
RFLAGS：Fatfor的Fortran编译器参数
LFLAGS：Lex文法分析器参数
YFLAGS：Yacc文法分析器参数
COFLAGS：RCS命令参数
GFLAGS：SCCS get参数

隐含规则链

make会努力自动推导生成目标的一切方法，无论中间目标 数量，都会将显式规则、隐含规则结合分析以生成目标

中间目标不存在才会引发中间规则
目标成功产生后，中间目标文件被删除
- 可以使用.SECONDARY强制声明阻止make删除该中间目标
- 指定某模式为伪目标.PRECIOUS的依赖目标，以保存被隐含规则生成的符合该模式中间文件
通常makefile中指定成目标、依赖目标的文件不被当作中间目标，可以用.INTERMEDIATE强制声明目标（文件）是中间目标
make会优化特殊的隐含规则从而不生成中间文件，如从文件 foo.c直接生成可执行文件foo

模式规则

模式规则：隐式规则可以看作内置模式规则

目标定义包含%，表示任意长度非空字符串

依赖中同样可以使用%，但是其取值取决于目标

命令中不使用模式%，使用自动化变量

模式规则没有确定目标，不能作为最终make目标
- 但是符合模式规则的某个具体文件可以作为最终目标
- 不需要作为显式规则的目标，如：archive(member)作为静态库隐含规则目标
模式的启用取决于其目标，%的解析同样取决于目标 （因为根据目标查找、应用模式规则）
模式规则类似于隐含规则，给出符合某个模式的某类目标的依赖、生成命令
%的展开发生在变量、函数展开后，发生在运行时

静态模式

静态模式：给定目标候选范围的模式，限制规则只能应用在以给定范围文件作为目标的情况

1 2	<target>: <target-pattern>: <prereq-patterns> <commands>

<target>：目标候选范围，可含有通配符

<target-pattern>：所有目标文件满足的模式

<prereq-pattern>：目标相应依赖

简单例子

objects = foo.o bar.o
all: $(objects)
$(objects): %.o: %.c
	$(CC) -c $(CFLAGS) $< -o $@

	# 等价于

foo.o: foo.c
	$(CC) -c $(CFLAGS) foo.c -o foo.o
bar.o: bar.c
	$(CC) -c $(CFLAGS) bar.c -o bar.o

静态模式+filter函数筛选范围

files = foo.elc bar.o lose.o
$(filter %.o,$(files)): %.o: %.c
	$(CC) -c $(CFLAGS) $< -o $@
$(filter %.elc,$(files)): %.elc: %.el
	emacs -f batch-byte-compile $<

重载内建隐含规则

%.o: %c
	$(CC) -c $(CPPFLAGS) $(CFLAGS) -D $(date)
	# 重载内建隐含规则
%o: %c
	# 命令置空，取消内建隐含规则

后缀规则

双后缀规则：定义一对目标文件后缀、依赖后缀

单后缀规则：定义一个依赖后缀

.c.o:
	# 等价于`%.o: %c`
	$(CC) -c $(CFLAGS) $(CPPFLAGS) -o $@ $<
.c:
	# 等价于`%: %.c`
	$(CC) -c $(CFLAGS) $(CPPFLAGS) -o $@ $<

后缀规则中不能有任何依赖文件，否则不是后缀规则，后缀被认为是目标文件
后缀规则中必须有命令，否则没有任何意义，这不会移去内建的隐含规则
后缀规则定义中的后缀需要是make所认识的，可以使用伪目标 .SUFFIXES修改make认识的后缀
1
2
3
4
.SUFFIXES:
# 删除默认后缀
.SUFFIXES: .c .o .h
# 添加自定义后缀
- 变量$SUFFIXE用于定义默认后缀列表，不应该修改
- -r/--no-builtin-rules同样会清空默认后缀列表
后缀规则是老式定义隐含规则的方法，会被逐步取代，事实上后缀规则在makefile载入后会被转换为模式规则

模式规则搜索算法

设目标为src/foo.o

将目标目录部分、文件名部分分离，得到src/、foo.o
搜索所有模式规则列表，创建目标和src/foo.o匹配的模式规则列表
- 若模式规则列表中有目标匹配所有文件的模式（如%），则从列表中移除其他模式
- 移除列表中没有命令的规则
对列表中首个模式规则
- 将src/foo.o或foo.o匹配目标，推断%匹配非空部分茎S
- 把依赖中%替换为茎S，如果依赖项中没有包含目录，尝试将src添加在其前
- 检查所有依赖文件存在、理当存在（文件被定义为其他规则的目标文件、显式规则的依赖文件）
- 若有依赖文件存在、理当存在或没有依赖文件，此规则被采用，退出算法
若没有找到合适模式规则，则检查列表中下个规则是否可行
若没有模式规则可以使用，检查.DEFAULT规则存在性，存在则应用

变量、赋值

Makefile中定义的变量类似C++/C中的宏

代表一个字符串，在makefile中执行的时候展开在所在位置

""会被作为字符串一部分

默认空格、逗号分隔列表

empty:=
space:=$(empty) # 后面有空格，就得到了空格
comma:=,
foo:=a,b,c
bar:=$(substr $(comma), $(space), $(foo)) # 得到字符串`a b c`

变量可以改变值

在shell中需要$$处应使用两个$$$，一个$被escape，则 shell解释时仍然保留一个$，如：变量、函数等都需要

赋值

Makefile内自定义变量

txt = Hello World
	# 自定义变量
test:
	@echo $(txt)
	echo ${txt}
	# 调用变量，`()`、`{}`含义相同
	# 若变量名为单个字符，可以省略括号，但不建议省略

=：lazy set，在执行时扩展
- 可以使用任意位置定义（可能还未定义）的变量赋值
- 允许递归扩展，make报错
:=：immediate set，在定义/赋值时扩展完毕
- 只允许使用之前已定义变量赋值（否则为空）
?=：set if absent，只有变量为空时才设置值
+=：append，将值追加到变量的尾部
- 若前面变量有定义，+=会继承前一次操作符:=/=
- 对于=定义变量，make自动处理“递归”

`define`

define可以换行定义变量

变量类似宏的行为、可换行定义变量，方便定义命令包

define run-yacc
	# `define`后跟变量名作为命令包名称
	yacc $(firstword $^); \
	mv y.tab.c $@
endef
	# 结束定义

foo.c: foo.y
	$(run-yacc)
	# 使用命令包

`override`

若变量由make命令行参数-e设置，makefile中默认忽略对其赋值
需要显式使用override关键字设置

1
2
3

override <variable> = <value>
override <variable> := <value>
override define <variable>

`export`

上级makefile中变量可以显式export传递到下层makefile中，但是不会覆盖下层中定义的变量（除指定-e参数）

export <variable>[=value]
	# 传递变量至下级makefile中
unexport <variable>
	# 禁止变量传递至下级makefile中

export variable = value
	# 等价
variable = value
export variable

export后面不指定具体传递变量，表示传递所有变量
MAKEFLAGS、SHELL两个变量总是会传递到下级makefile中

系统环境变量

make运行时系统环境变量、命令行环境变量可以被载入makefile

默认makefile中定义变量覆盖系统环境变量
-e参数则表示makefile中变量被覆盖

1
2
3

test:
	@echo $$HOME
	# 传递给shell的变量，需要`$$` escape

Target-Specific Variable

目标/局部变量：作用范围局限于规则、连带规则中

<target ...>: [override] <variable-assignment>

prog: CFLAGS  = -g
prog: prog.o foo.o bar.o
	$(CC) $(CFLAGS) prog.o foo.o bar.o

prog.o: prog.c
	$(CC) $(CFLAGS) prog.c

foo.o: foo.c
	$(CC) $(CFLAGS) foo.c

bar.o: bar.c
	$(CC) $(CFLAGS) bar.c

Pattern-Specific Variable

模式变量：给定模式，变量定义在符合模式的所有目标上

1
2
3

<pattern ...>: [override]<variable-assignment>

%.o: CFLAGS = -o

Implicit Variables

内置变量：主要是为了跨平台的兼容性

$(CC)：当前使用的编译器
1
2
output:
$(CC) -o output input.c
$(MAKE)：当前使用的Make工具
$(MAKECMDGOLA)：make目标列表

Automatic Variables

自动化变量：应用规则时被自动赋予相应值（一般是文件）的变量

$@：当前需要生成的目标文件
- 多目标规则中，$@也只表示被需要目标
$*：匹配符%匹配部分
- 若目标中没有%模式符，$*不能被推导出，为空
- GNU make中，目标中没有%，$*被推导为除后缀部分，但是很可能不兼容其他版本，谨慎使用
$<：首个前置条件
$%：仅当目标是函数库文件，表示目标成员名，否则为空
- 目标为foo.a(bar.o)：$%为bar.o、$@为foo.a
$?：比目标更新的前置条件，空格分隔
$^：所有前置条件，会取出其中重复项
$+：类似于$^，但是剔除重复依赖项

自动化变量只应出现在规则的命令中

自动化变量值与当前规则有关

其中$@、$*、$<、$%扩展后只会为单个文件，$?、 $^、$+扩展后可能是多个文件

1
2
3

dest/%.txt: src/%.txt
	@[ -d test ] || mkdir dest
	cp $< $@

D、F

7个自动化变量可以搭配D、F取得相应路径中目录名、文件名
新版本GNU make可以使用函数dir、notdir代替D/F

D/dir：目录带有最后/，若为当前目录则为./

F/nodir：文件名

对可能会扩展为多文件的$?、$^、$+，D/F处理后返回同样是多个目录/文件

$(@D)
$(dir $@)
	# `$@`的目录名
$(@F)
$(nodir $@)
	# `$@`的文件名

$(?D)
$(dir $?)
	# `$?`中所有目录，空格分隔
$(?F)
$(nodir $?)
	# `$?`中所有文件，空格分隔

控制语句

`if`


<conditional-directive>
<text-if-true>
[
else
<text-if-false>
]
endif

ifeq：比较参数是否相等

ifneq：比较参数是否不等

ifeq ($(CC), gcc)
	# 也可以用单/双引号括起，省略括号
	libs=$(libs_for_gcc)
else
	libs=$(normal_libs)
endif

ifdef

bar =
foo = $(bar)
# `foo`有定义
ifdef foo
	frobozz = yes
	# 此分支
else
	frobozz = no
endif

foo =
# `foo`未定义
ifdef foo
	frobozz = yes
else
	frobozz = no
	# 此分支
endif

ifndef

<conditional-directive>, else, endif行可以有多余空格，但是不能以<tab>开头，否则被认为是命令

make在读取makefile时就计算表达式值、选择语句，所以最好别把自动化变量放入条件表达式中

make不允许把条件语句分拆放入两个文件中

`for`

LIST = one two three

all:
	for i in $(LIST); do \
		echo $$i;
		// 这里传递给shell的变量，需要`$$` escape
	done
all:
	for i in one two three; do
		echo $$i;
	done

内建函数

1 2	$(function parameters) ${function paremeters}

Make控制函数

提供一些函数控制make执行

检测运行makefile的运行时信息，根据信息决定make继续执行、停止

`error`

产生错误并退出make，错误信息<text>

$(error <text...>)

ifdef ERROR_001
$(error error is $(ERROR_001))
endif

ERR = $(error found an error)
.PHONY: err
err:
	err: ; $(ERR)

`warning`

类似error函数，输出警告信息，继续make

其他函数

`shell`

执行shell命令的输出作为函数返回值

1	srcfiles := $(shell echo src/{00..99}.txt)

函数会创建新shell执行命令，大量使用函数可能造成性能下降，尤其makefile的隐晦规则可能让shell函数执行次数过多

`wildcard`

在变量中展开通配符*

1
2
3

srcfiles := $(wildcard src/*.txt)
	# 若不展开，则`srcfiles`就只是字符串
	# 展开后则表示所有`src/*.txt`文件集合

字符串处理函数

`subst`

文本替换

$(subst <from>,<to>,<text>)
	# `subst`函数头

$(subst ee,EE,feet on the street)
	# 替换成*fEEt on the strEET*

`patsubst`

模式匹配的替换

$(patsubst <pattern>,<replacement>,<text>)
	# 函数头文件
$(patsubst %.c,%o,x.c.c bar.c)
	# 替换为`x.c.o bar.o`

foo := a.o b.o c.o
$(variable: <pattern>=<replacement>)
	# `patsubst`函数的简写形式
bar := $(foo:%.o=%.c)
	# `$(bar)`变为`a.c b.c c.c`

$(variable: <suffix>=<replacement>)
	# 没有模式匹配符`%`则替换结尾
bar := $(foo:.o=.c)
	# `$(bar)`变为`a.c b.c c.c`

`strip`

去字符串头、尾空格

1 2	$(strip <string>) $(strip a b c)

`findstring`

在<in>中查找<find>，找到返回<find>，否则返回空串

1 2	$(findstring <find>,<in>) $(findstring a,a b c)

`filter`

以<pattern>模式过滤<text>字符串中单词，返回符合模式的单词

$(filter <pattern..>,<text>)

sources := foo.c bar.c baz.s ugh.h
foo: $(sources)
	cc $(filter %.c %.s, $(sources)) -o foo
	# 返回`foo.c bar.c baz.s`

`filter-out`

以<pattern>模式过滤<text>字符串中单词，返回不符合模式的单词

objects := main1.o foo.o main2.o bar.o
mains=main1.o main2.o
$(filter-out $(mains), $(objects))
	# 返回`foo.o bar.o`

`sort`

对<list>中单词升序排序

$(sort <list>)

$(sort foo bar lose)
	# 返回`bar foo lose`

`word`

取字符串<text>中第<n>个单词

$(word <n>,<text>)

$(word 2, foo bar baz)
	# 返回`bar`

`wordlist`

从<text>中取<s>-<e>单词（闭区间）

$(wordlist <s>,<e>,<text>)

$(wordlist 2, 3, foo bar baz)
	# 返回`bar baz`

`words`

统计<text>中单词个数

$(word <text>)

$(word, foo bar baz)
	# 返回3

`firstword`

取<text>中首个单词

$(firstword <text>)

$(firstword foo bar)
	# 返回`foo`

文件名操作函数

`dir`

从文件名序列中取出目录部分

最后/之前部分
若没有/则返回./

$(dir <names...>)

$(dir src/foo.c hacks)
	# 返回`src/ ./`

`notdir`

从文件名序列中取出非目录部分（最后/之后部分）

$(notdir <names...>)

$(notdir src/foo.c hacks)
	# 返回`foo.c hacks`

`suffix`

从文件名序列中取出各文件名后缀

$(suffix <names...>)

$(suffix src/foo.c src-1.0/bar.c hacks)
	# 返回`.c .c`

`basename`

从文件名序列中取出各文件名“前缀”（除后缀外部分）

$(basename <names...>)

$(basename src/foo.c src-1.0/bar.c hacks)
	# 返回`src/foo src-1.o/bar hacks`

`addsuffix`

把后缀<suffix>添加到文件名序列中每个单词后

$(addsuffix <suffix>,<names...>)

$(addsuffix .c, foo bar)
	# 返回`foo.c bar.c`

`addprefix`

把后缀<prefix>添加到文件名序列中每个单词后

$(addprefix <prefix>,<names...>)

$(addprefix src/, foo bar)
	# 返回`src/foo src/bar`

`join`

把<list2>中单词对应添加到<list1>中单词后

较多者剩余单词保留

$(join <list1>,<list2>)

$(join aaa bbb, 111 222 333)
	# 返回`aaa111 bbb222 333`

控制函数

`foreach`

循环函数，类似于Bash中的for语句

把<list>中单词逐一取出放到参数<var>所指定的变量中
再执行<text>所包含的表达式，每次返回一个字符串
循环结束时，返回空格分隔的整个字符串

$(foreach <var>,<list>,<text>)

names := a b c d
files := $(foreach n,$(names),$(n).o)
	# 返回`a.o b.o c.o d.o`

<var>是临时局部变，函数执行完后将不再作用

`if`

类似于make中的ifeq

<condition>为真（非空字符串），计算<then-part>返回值
<condition>为假（空字符串），计算<else-part>、返回空字符串

1	$(if <condition>,<then-part>,[<else-part>])

`call`

创建新的参数化函数的函数

创建表达式<expression>，其中可以定义很多参数
用call函数向其中传递参数，<expression>返回值即call 返回值

$(call <expression>,<param1>,<param2>,...>

reverse = $(1) $(2)
foo = $(call reverse,a,b)
	# 返回`a b`
reverse = $(2) $(1)
foo = $(call reverse,a,b)
	# 返回`b a`

<expression>要先创建为变量，然后不带$传递

`origin`

返回变量的来源

undefined：<variable>未定义
default：make默认定义变量
environment：环境变量，且-e选项未开
file：定义在makefile中
command line：命令行定义环境变量
override：override关键字定义
atomatic：命令运行中自动化变量

$(origin <variable>)

ifdef bletch
ifeq "$(origin bletch)" "environment"
bletch = barf, gag, etc
endif
endif

<variable>不操作变量值，不带$传递

Makefile技巧

案例

edit: main.o kdd.o command.o display.o \
	insert.o search.o files.o utils.o
	cc -o edit main.o kbd.o command.o dispaly.o\
		insert.o search.o files.o utils.o

main: main.c defs.h
	cc -c main.c
kbd.o: kbd.c defs.h
	cc -c kbd.c
command.o: command.c defs.h command.h
	cc -c command.c
display.o: display.o defs.h buffer.h
	cc -c display.c
insert.o: insert.c defs.h buffer.h
	cc -c insert.c
search.o: search.c defs.h buffer.h
	cc -c search.c
files.o: files.c defs.h buffer.h command.h
	cc -c files.c
utils.o utils.c defs.h
	cc -c utils.c

clean:
	rm edit main.o kbd.o command.o display.o \
		insert.o search.o files.o utils.o

.PHONY: edit clean
	# 设置`edit`、`clean`为伪目标

利用变量简化目标

objects = main.o kbd.o command.o display.o \
	insert.o search.o files.o utils.o

edit: $(objects)
	cc -o edit $(objects)
	# 以下同上

隐式模式自动推导

objects = main.o kbd.o command.o display.o \
	insert.o search.o files.o utils.o
edit: $(objects)
	cc -o edit $(objects)
main.o: defs.h
kbd.o: defs.h command.h
command.o: defs.h command.h
display: defs.h buffer.h
insert.o: defs.h buffer.h
search.o: defs.h buffer.h
files.o: defs.h buffer.h command.h
utils.o: defs.h

clean:
	rm edit $(objects)

.PHONY: clean

利用隐式模式自动推导文件、文件依赖关系

利用变量提取依赖

objects = main.o kbd.o command.o display.o \
	insert.o search.o files.o utils.o
edit: $(objects)
	cc -o edit $(objects)

$(objects): defs.h
kbd.o command.o files.o: command.h
display.o insert.o search.o files.o: buffer.h

clean:
	rm edit $(objects)

.PHONY: clean

文件变得简单，但是依赖关系不再清晰

自动生成依赖

大部分C++/C编译器支持-M选项，自动寻找源文件中包含的头文件，生成依赖关系
GNU建议为每个源文件自动生成依赖关系，存放在一个文件中，可以让make自动更新依赖关系文件.d，并包含在makefile中

%.d: %.c
	@set -e; rm -f $@; \
	$(cc) -M $(CPPFLAGS) $< > $@.$$$$; \
		# 生成中间文件
		# `$$$$`表示4位随机数
	sed 's,/($*/)/.o[ :]*,/1.o $@ : ,g' < $@.$$$$ > $@; \
		# 用`sed`替换中间文件target
		# `xxx.o` -> `xxx.o xxx.d`
	rm -f $@.$$$$
		# 删除中间文件

source = foo.c bar.c
include $(sources: .c=.d)

Posted 2019-07-11Updated 2019-07-11Database / Sparka minute read (About 169 words)

Spark GraphX

GraphX

Spark GraphX：图数据的并行处理模块

GraphX扩展RDD为Resilient Distributed Property Graph，边、顶点都有属性的有向图
可利用此模块对图数据进行ExploratoryAnalysis、Iterative Graph Computation
GraphX提供了包括：子图、顶点连接、信息聚合等操作在内的基础原语，并且对的Pregel API提供了优化变量的
GraphX包括了正在不断增加的一系列图算法、构建方法，用于简化图形分析任务
- 提供了一系列操作
  - Sub Graph：子图
  - Join Vertices：顶点连接
  - Aggregate Message：消息聚集
  - Pregel API变种
- 经典图处理算法
  - PageRank

Posted 2019-07-11Updated 2021-07-19Database / Spark6 minutes read (About 869 words)

Spark MLLib

MLLib

Spark MLLib：Spark平台的机器学习库

能直接操作RDD数据集，可以和其他BDAS其他组件无缝集成，使得在全量数据上进行学习成为可能
实现包括以下算法
- Classification
- Regression
- Clustering
- Collaborative Filtering
- Dimensionality Reduction
MLLib是MLBase中的一部分
- MLLib
- MLI
- MLOptimizer
- MLRuntime
从Spark1.2起被分为两个模块
- spark.mllib：包含基于RDD的原始算法API
- spark.ml：包含基于DataFrame的高层次API
  - 可以用于构建机器学习PipLine
  - ML PipLine API可以方便的进行数据处理、特征转换、正则化、联合多个机器算法，构建单一完整的机器学习流水线

MLLib算法代码可以在examples目录下找到，数据则在data 目录下

机器学习算法往往需要多次迭代到收敛为止，Spark内存计算、 DAG执行引擎象相较MapReduce更理想

由于Spark核心模块的高性能、通用性，Mahout已经放弃 MapReduce计算模型，选择Spark作为执行引擎

`mllib.classification`

Classification

Logistic Regression

from pyspark.mllib.classification import \
	LogisticRegressionWithLBFGS, LogisticRegressionModel
from pyspark.mllib.regression import LabledPoint

def parse_point(line):
	value = [float(i) for i line.split(", \r\n\t")

data = sc.textFile("data/mllib/sample_svm_data.txt")
parsed_data = data.map(parse_point)
	# map `parse_point` to all data

model = LogisticRegressionWithLBFGS.train(parsed_data)
labels_and_preds = parsed_data.map(lambda p: (p.label, model.predict(p.features)))
train_err = labels_and_preds \
	.filter(lambda lp: lp[0] != lp[1]) \
	.count() / float(parsed_data.count())

model.save(sc, "model_path")
same_model = LogisticRegressionModel.load(sc, "model.path")

Decision Tree
Random Forest
Gradient
boosted tree
Multilaye Perceptron
Support Vector Machine
One-vs-Rest Classifier
Naive Bayes

Clustering

K-means

import numpy as np
from pyspark.mllib.clustering import KMeans, KMeansModel

data = sc.textFile("data/mllib/kmeans_data.txt")
parsed_data = data.map(lambda line: np.array([float(i) for i in line.split()]))

cluster_model = KMeans.train(
	parsed_data,
	maxIteration=10,
	initializationMode="random"
)
def error(point):
	center = cluster_model.centers[cluster.predict(point)]
	return np.sqrt(sum([i**2 for i in (point - center)]))
WSSSE = parsed_data \
	.map(lambda point.error(point)) \
	.reduce(lambd x, y: x + y)

cluster_model.save(sc, "model_path")
same_model = KMeansModel.load(sc, "model_path")

Gaussian Mixture Model(GMM)

混合密度模型
- 有限混合模型：正态分布混合模型可以模拟所有分布
- 迪利克莱混合模型：类似于泊松过程
应用
- 聚类：检验聚类结果是否合适
- 预测：
  todo

import numpy as np
from pyspark.mllib.clustering import GussianMixture, \
	GussianMixtureModel

data = sc.textFile("data/mllib/gmm_data.txt")
parsed_data = data.map(lambda line: np.array[float(i) for i in line.strip()]))

gmm = GaussianMixture.train(parsed_data, 2)
for w, g in zip(gmm.weights, gmm.gaussians):
	print("weight = ", w,
		"mu = ", g.mu,
		"sigma = ", g.sigma.toArray())

gmm.save(sc, "model_path")
same_model = GussainMixtureModel.load(sc, "model_path")

Latent Dirichlet Allocation(LDA)

from pyspark.mllib.clustering import LDA, LDAModel
from pyspark.mllib.linalg import Vectors

data = sc.textFile("data/mllib/sample_lda_data.txt")
parsed_data = data.map(lambda line: Vector.dense([float(i) for i in line.strip()]))

corpus = parsed_data.zipWithIndex() \
	.map(lambda x: [x[1], x[0]).cache()
ldaModel = LDA.train(corpus, k=3)

topics = ldaModel.topicsMatrix()

for word in range(0, ldaModel.vocabSize()):
	for topic in word:
		print(topic)

ldaModel.save(sc, "model_path")
same_model = LDAModel.load("model_path")

Disecting K-means

Regression

Linear Regression

耗时长、无法计算解析解（无意义）
使用MSE作为极小化目标函数，使用SGD算法求解

from pyspark.mllib.regression import LabledPoint, \
	LinearRegressionWithSGD, LinearRegressionModel

def parse_point(line):
	value = [float(i) for i line.split(", \r\n\t")

data = sc.textFile("data/mllib/ridge-data/lpsa.data")
parsed_data = data.map(parse_point)
	# map `parse_point` to all data

model = LinearRegressionWithSGD.train(
	parsed_data,
	iteration=100,
	step=0.00000001
)
values_and_preds = parsed_data.map(lambda p:(p.label, model.predict(p.features)))
MSE = values_and_preds \
	.map(lambda vp: (vp[0] - vp[1]) ** 2) \
	.reduce(lambda x, y: x + y) / values_and_preds.count()

model.save(sc, "model_path")
	# save model
same_model = LinearRegressionModel.load(sc, "model_path")
	# load saved model

Generalized Linear Regression
Decision Tree Regression
Random Forest Regression
Gradient-boosted Tree Regression
Survival Regression
Isotonic Regression

Collaborative Filtering

Posted 2019-07-11Updated 2021-08-02Database / Spark5 minutes read (About 758 words)

Spark SQL

Spark SQL：结构化数据查询模块

内置JDBC服务器，通过JDBC API暴露Spark数据集，让客户程序可以在其上直接执行SQL查询
通过ETL工具从不同格式数据源装载数据，并运行一些 Ad-Hoc Query
可以连接传统的BI、可视化工具至数据集

前身Shark即为Hive on Spark，后出于维护、优化、性能考虑放弃

Extraction Transformation Loading：ETL

sparksql_structure

sql.SQLContext

import org.apache.spark.sql.{SQLContext, HiveContext}

class SQLContext{

	// 缓存使用柱状格式的表
	// Spark将仅仅浏览需要的列、自动压缩数据减少内存使用
	def cacheTable(tableName: String)

	// 将普通RDD转换为SchemaRDD
	def implicit createSchemaRDD(rdd: RDD): SchemaRDD

	// 载入parquet格式文件
	def parquetFile(fileName: String): SchemaRDD

	// 载入json格式文件
	def jsonFile(fileName: String): SchemaRDD
	def jsonRDD(rdd: RDD[String]): SchemaRDD

	// 执行SQL query
	def sql(query: String): SchemeRDD
}

HiveContext支持SQLContext支持功能的超集，增加在 MetaStore发现表、利用HiveSQL写查询功能

`sql.SchemaRDD`

class SchemaRDD{

	// 存储为parquet文件
	def saveAsParquetFile(fileName: String)

	// 注册为临时表，然后可以使用SQL语句查询
	def registerTempTable(tableName: String)

	// 打印表schema
	def printSchema()
}

在数据存储层面对数据进行结构化描述的schema

由SchemaRDD（上个版本）发展而来，在其上增加schema层，以便对各个数据列命名、数据类型描述
可以通过DF API把过程性处理、Relational Processing （对表格的选择、投影、连接等操作）集成
DF API操作是Lazy的，使得Spark可以对关系操作、数据处理工作流进行深入优化
结构化的DF可以通过调用DF API重新转换为无结构的RDD数据集
可以通过不同Data Source创建DF
- 已经存在的RDD数据集
- 结构化数据文件
- JSON数据集
- Hive表格
- 外部数据库表

Data Source

数据源：通过DS API可以存取不同格式保存的结构化数据

Parquet
JSON
Apache Avro数据序列化格式
JDBC DS：可以通过JDBC读取关系型数据库

import org.apache.spark.sql.{SQLContext, StructType, StructField, Row}
import org.apache.spark.sql.HiveContext

val sqlContext = new SQLContext(sc)
import sqlContext.createSchemeRDD


case class Person(name: String, age: Int)

// 通过反射推断包含特定对象类型的RDD的模式
// 需要编写时已知模式
// 代码更简洁、工作更好
val people: RDD[Person] = sc.textFile("people.txt")
	.map(_.split(","))
	.map(p => Person(p(0), p(1).trim.toInt))


// 编程指定模式：构建模式，然后在已经存在的RDDs上使用
// 运行在运行期前不知道列、列类型情况下构造SchemaRDDs
val schemaString = "name age"
val people = sc.textFile("people.txt")
val schema = StructType(schemaString.split(" ")
	.map(fieldName => StructField(fieldName, StringType, true))
)
val rowRDD = people.map(_.split(","))
	.map(p => Row(p(0), p(1).trim))
val peopleSchemaRDD = sqlContext.applySchema(rowRDD, schema)
peopleSchemaRDD.registerTempTable("people")


// 查询语言集成
val teenagers = people.where("age >= 13").select("name")


people.registerTempTable("people")
val teenagers = sqlContext.sql("SELECT name FORM people WHERE age >= 13")


val apRDD = sc.parallelize(
	"""{"name": "Tom", "address": { "city": "Columbus", "state": "Ohio" }}""" :: Nil)
val anotherPeople = sqlContext.jsonRDD(apRDD)