Emsemble Learning
- 集成学习:训练多个基模型,并将其组合起来,以达到更好的
预测能力、泛化能力、稳健性
- base learner:基模型,基于独立样本建立的、一组
具有相同形式的模型中的一个
- 组合预测模型:由基模型组合,即集成学习最终习得模型
源于样本均值抽样分布思路
- $var(\bar{X}) = \sigma^2 / n$
- 基于独立样本,建立一组具有相同形式的基模型
- 预测由这组模型共同参与
- 组合预测模型稳健性更高,类似于样本均值抽样分布方差
更小
关键在于
分类
|
Target |
Data |
parallel |
Classifier |
Aggregation |
| Bagging |
减少方差 |
基于boostrap随机抽样,抗异常值、噪声 |
模型间并行 |
同源不相关基学习器,一般是树 |
分类:投票、回归:平均 |
| Boosting |
减少偏差 |
基于误分分步 |
模型间串行 |
同源若学习器 |
加权投票 |
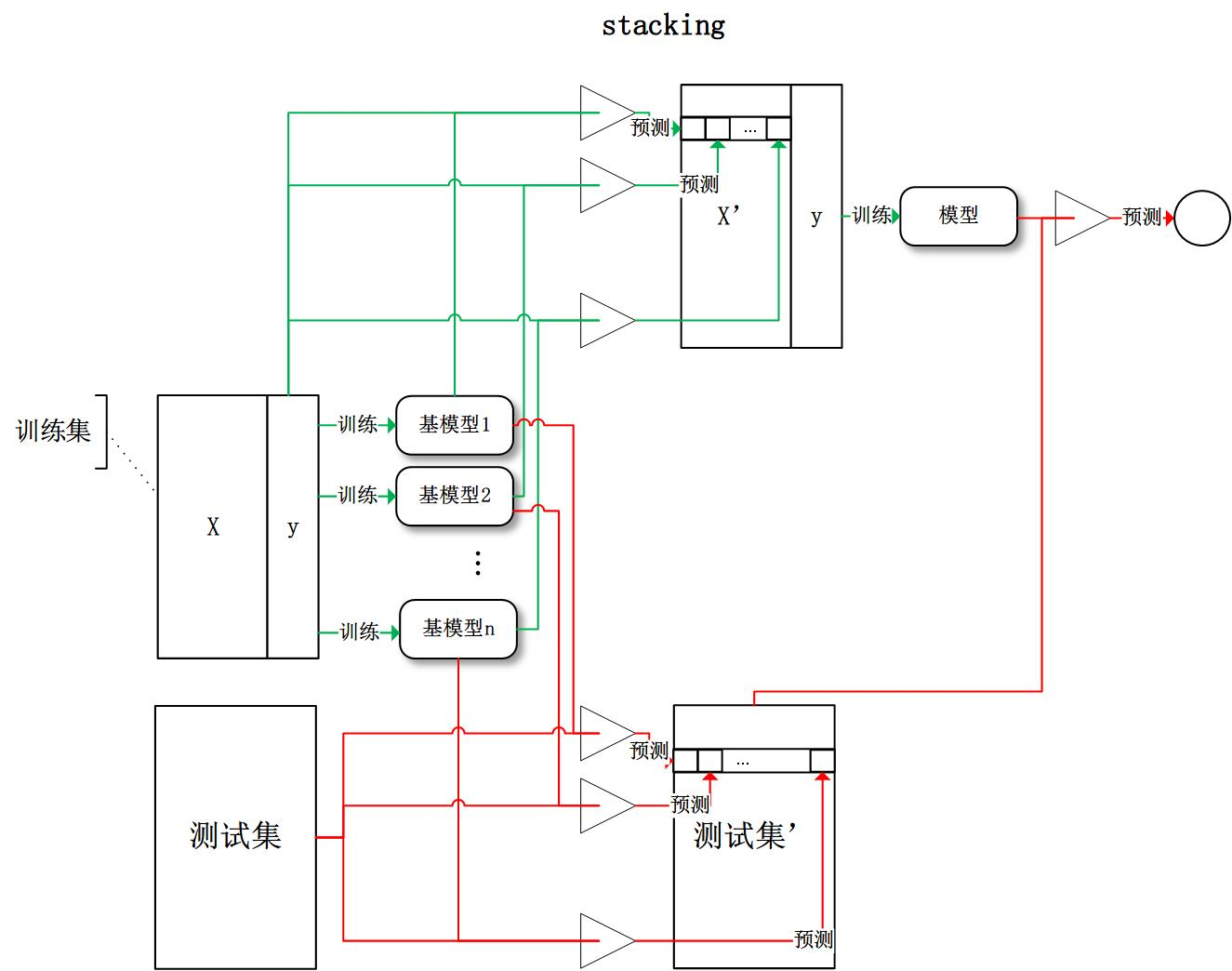
| Stacking |
减少方差、偏差 |
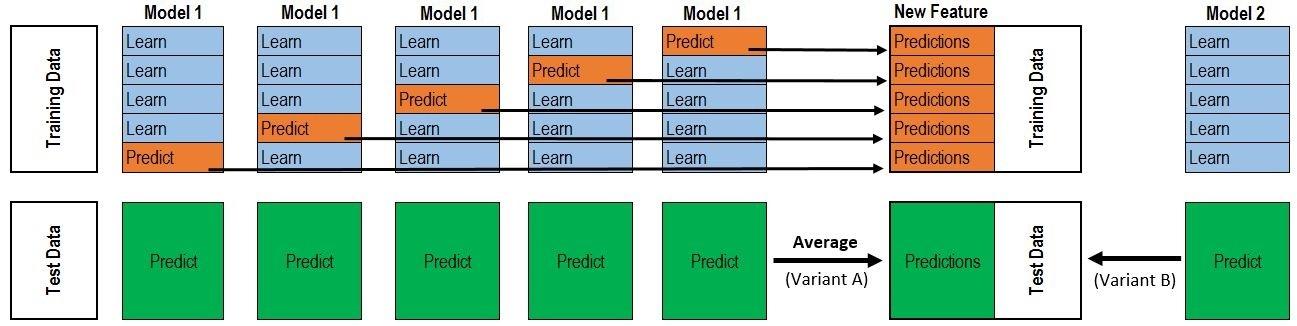
K折交叉验证数据、基学习器输出 |
层内模型并行、层间串行 |
异质强学习器 |
元学习器 |
Boosting
提升方法:将弱可学习算法提升为强可学习算法的组合元算法
- 属于加法模型:即基函数的线性组合
- 各模型之间存在依赖关系
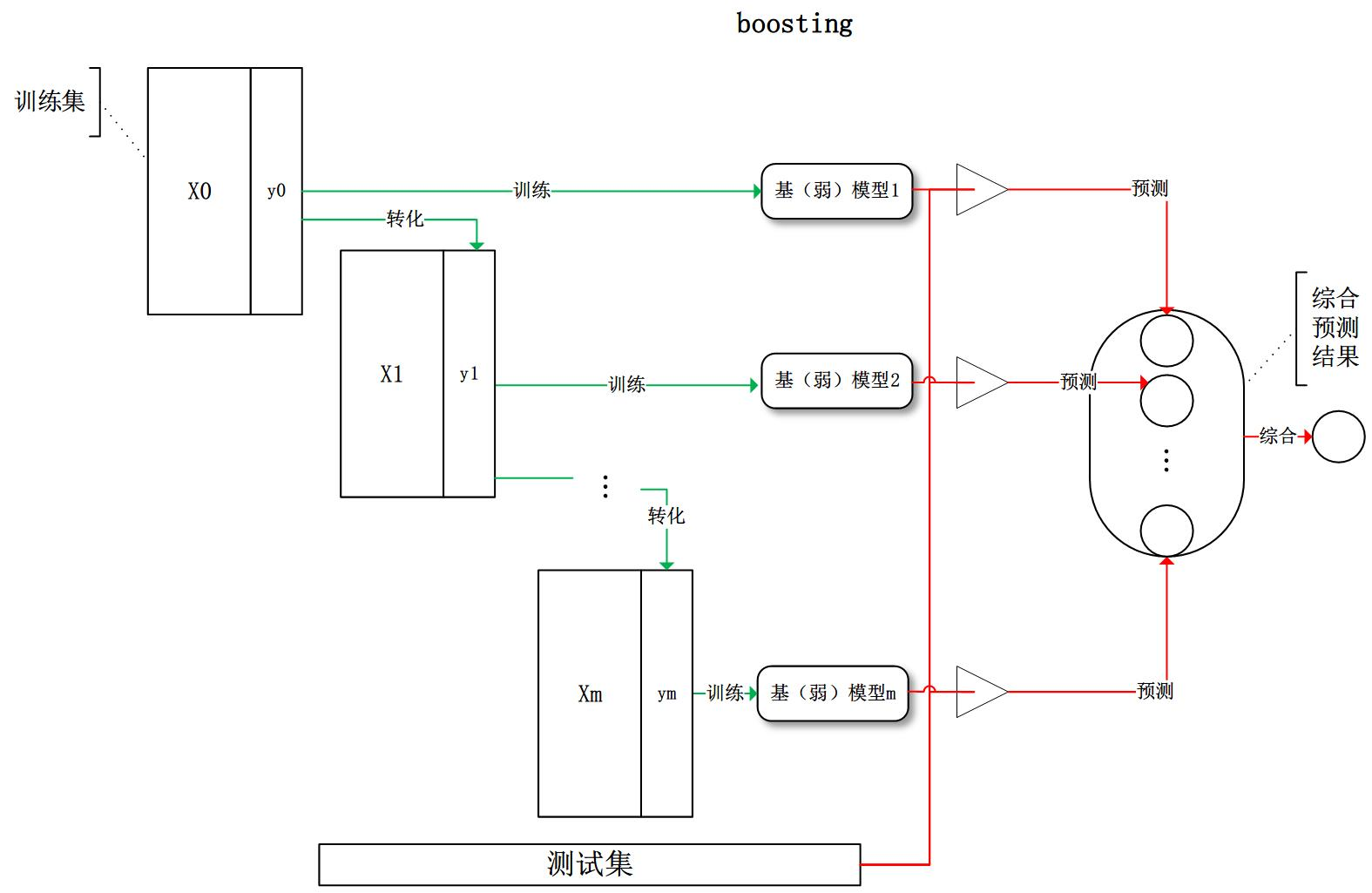
分类Boosting
- 依次学习多个基分类器
- 每个基分类器依之前分类结果调整权重
- 堆叠多个分类器提高分类准确率
回归Boosting
- 依次训练多个基学习器
- 每个基学习器以之前学习器拟合残差为目标
- 堆叠多个学习器减少整体损失
boosting组合模型整体损失(结构化风险)
- $l$:损失函数
- $f_t$:基学习器
- $\Omega(f_t)$:单个基学习器的复杂度罚
- $N, M$:样本数目、学习器数目
基学习器损失
最速下降法
使用线性函数拟合$l(y_i, \hat y_i^{(t)})$
- $gi = \partial{\hat y} l(y_i, \hat y^{t-1})$
- 一次函数没有极值
- 将所有样本损失视为向量(学习器权重整体施加),则负梯度
方向损失下降最快,考虑使用负梯度作为伪残差
Newton法
使用二次函数拟合$l(y_i, \hat y_i^{(t)}$
- $hi = \partial^2{\hat y} l(y_i, \hat y^{t-1})$
- 二次函数本身有极值
- 可以结合复杂度罚综合考虑,使得每个基学习器损失达到最小
Boosting&Bagging
- 结论来自于Experiments with a New Boosting Algorithm
Boosting&Bagging
- 结论来自于Experiments with a New Boosting Algorithm
原理
probably approximately correct:概率近似正确,在概率近似
正确学习的框架中
strongly learnable:强可学习,一个概念(类),如果存在
一个多项式的学习算法能够学习它,并且正确率很高,那么
就称为这个概念是强可学习的
weakly learnable:弱可学习,一个概念(类),如果存在
一个多项式的学习算法能够学习它,学习的正确率仅比随机猜测
略好,称此概念为弱可学习的
Schapire证明:在PAC框架下强可学习和弱可学习是等价的
具体措施
- 弱学习算法要比强学习算法更容易寻找,所以具体实施提升就是
需要解决的问题
改变训练数据权值、概率分布的方法
将弱学习器组合成强学习器的方法
- competeing
- simple majority voting
- weighted majority voting
- confidence-based weighting
学习器组合方式
simple majority voting/simple average:简单平均
weighted majority voting/weighted average:加权平均
competing voting/largest:使用效果最优者
confidence based weighted:基于置信度加权
元学习:自动学习关于关于机器学习的元数据的机器学习子领域
要素
- 元学习系统必须包含子学习系统
- 学习经验通过提取元知识获得经验,元知识可以在先前单个
数据集,或不同的领域中获得
- 学习bias(影响用于模型选择的前提)必须动态选择
- declarative bias:声明性偏见,确定假设空间的形式
,影响搜索空间的大小
- procedural bias:过程性偏见,确定模型的优先级
Recurrent Neural networks
RNN:self-referential RNN理论上可以通过反向传播学习到,
和反向传播完全不同的权值调整算法
MetaRL:RL智能体目标是最大化奖励,其通过不断提升自己的学习
算法来加速获取奖励,这也涉及到自我指涉
Additional Model
加法模型:将模型视为多个基模型加和而来
- $b(x;\theta_m)$:基函数
- $\theta_m$:基函数的参数
- $\beta_m$:基函数的系数
Forward Stagewise Algorithm
前向分步算法:从前往后,每步只学习加法模型中一个基函数
及其系数,逐步逼近优化目标函数,简化优化复杂度
步骤
- 输入:训练数据集$T={(x_1,y_1), \cdots, (x_N,y_N)}$,损失
函数$L(y,f(x))$,基函数集${b(x;\theta)}$
- 输出:加法模型$f(x)$
AdaBoost&前向分步算法
AdaBoost(基分类器loss使用分类误差率)是前向分步算法的特例,
是由基本分类器组成的加法模型,损失函数是指数函数
基函数为基本分类器时加法模型等价于AdaBoost的最终分类器
$f(x) = \sum_{m=1}^M \alpha_m G_m(x)$
前向分步算法的损失函数为指数函数$L(y,f(x))=exp(-yf(x))$
时,学习的具体操作等价于AdaBoost算法具体操作
假设经过m-1轮迭代,前向分步算法已经得到
经过第m迭代得到$\alpha_m, G_m(x), f_m(x)$,其中
- $\bar w{m,i}=exp(-y_i f{m-1}(x_i))$:不依赖
$\alpha, G$
$\forall \alpha > 0$,使得损失最小应该有
(提出$\alpha$)
此分类器$G_m^{*}$即为使得第m轮加权训练误差最小分类器
,即AdaBoost算法的基本分类器
又根据
带入$G_m^{*}$,对$\alpha$求导置0,求得极小值为
即为AdaBoost中$\alpha_m$
对权值更新有
与AdaBoost权值更新只相差规范化因子$Z_M$