LightGBM

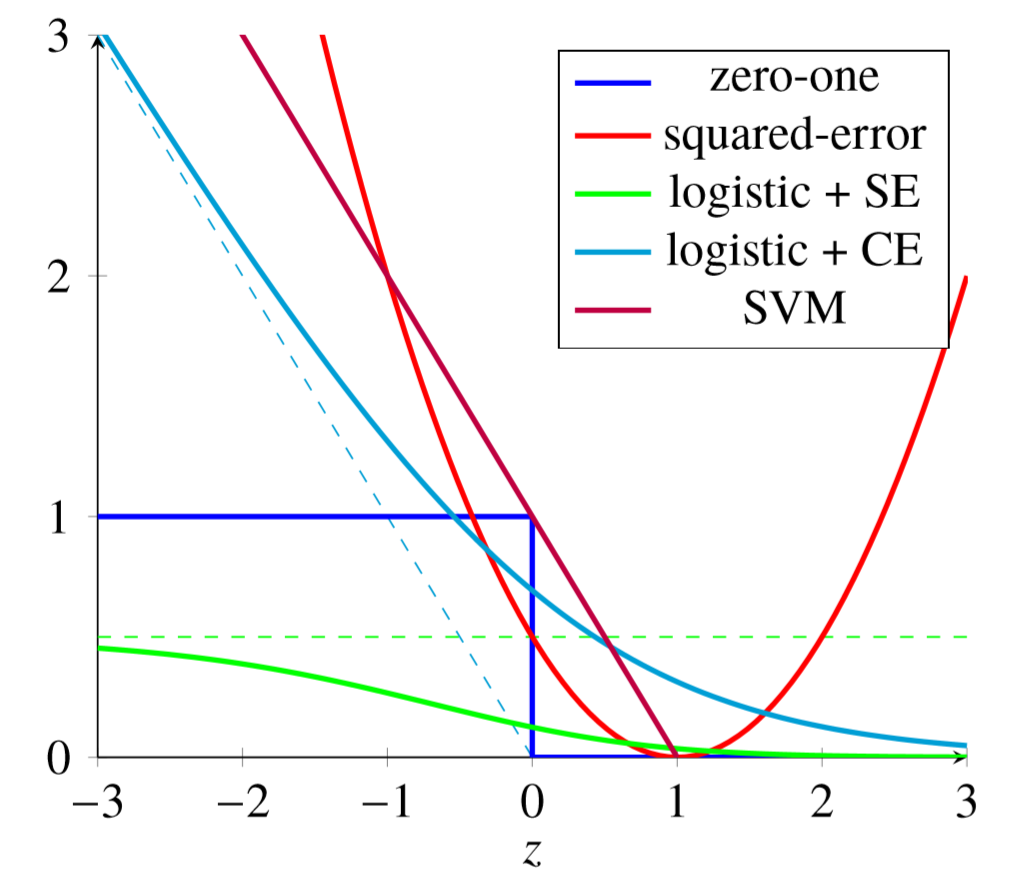
参数估计

• 矩估计：建立参数和总体矩的关系，求解参数

  • 除非参数本身即为样本矩，否则基本无应用价值
  • 应用场合
    • 均值：对应二次损失 $\arg\min{\mu} \sum{i=1}^N (x_i - \mu)^2$
    • 方差：对应二次损失?

• 极大似然估计：极大化似然函数，求解概率上最合理参数

  • 需知道（假设）总体 概率分布形式
  • 似然函数形式复杂，求解困难
    • 往往无法直接给出参数的解析解，只能求数值解
  • 应用场合
    • 估计回归参数：对数损失 $\mathop{\arg\min}{\beta} \sum{i=1}^N lnP(y_i|x_i, \beta)$

• 损失函数估计：极小化损失函数，求解损失最小的参数

  • 最泛用的参数求解方法
    • 适合求解有大量参数的待求解的问题
    • 往往通过迭代方式逐步求解
  • 特别的
    • 线性回归使用 MSE 作为损失函数时，也被称为最小二乘估计
    • 极大似然估计同对数损失函数

• 参数估计都可以找到合适损失函数，通过迭代求解损失最小化

随机模拟估计参数

• 需要设计随机模拟实验估计参数
• 应用场合
  • 蒙特卡洛类似算法：随机化损失

迭代求解参数

• 损失函数定义不同

  • 包含样本量数量不同
  • 惩罚项设置不同

• 异步更新参数

  • 同时求解参数数量：全部、部分、单个
  • 参数升维

• 更新方向

  • 梯度
  • 海瑟矩阵
  • 次梯度

• 更新方式

  • 叠加惯性
  • 动态学习率

Loss Models

模型（目标函数）在样本整体的损失：度量模型整体预测效果

• 代表模型在整体上的性质，有不同的设计形式

• 可以用于 设计学习策略、评价模型

  • 风险函数
  • 评价函数

• 有时在算法中也会使用整体损失

Expected Risk / Expected Loss / Generalization Loss

期望风险（函数）：损失函数 $L(Y, f(X))$（随机变量）期望

• $P(X, Y)$：随机变量 $(X, Y)$ 遵循的联合分布，未知

• 风险函数值度量模型预测错误程度

  • 反映了学习方法的泛化能力
  • 评价标准（监督学习目标）就应该是选择期望风险最小

• 联合分布未知，所以才需要学习，否则可以直接计算条件分布概率，而计算期望损失需要知道联合分布，因此监督学习是一个病态问题

Empirical Risk / Empirical Loss

经验风险：模型关于给定训练数据集的平均损失

• $\theta$：模型参数
• $D_i$：样本损失权重，常为 $\frac 1 N$，在 Boosting 框架中不同

• 经验风险损失是模型 $f(x)$ 的函数

  • 训练时，模型是模型参数的函数
  • 即其为模型参数函数

• 根据大数定律，样本量容量 $N$ 趋于无穷时，$R{emp}(f)$ 趋于 $R{exp}(f)$

  • 但是现实中训练样本数目有限、很小
  • 利用经验风险估计期望常常并不理想，需要对经验风险进行矫正

• 例子

  • maximum probability estimation：极大似然估计
    • 模型：条件概率分布（贝叶斯生成模型、逻辑回归）
    • 损失函数：对数损失函数

Structual Risk / Structual Loss

结构风险：在经验风险上加上表示 模型复杂度 的 regularizer（penalty term）

• $J(f)$：模型复杂度，定义在假设空间$F$上的泛函
• $\lambda$：权衡经验风险、模型复杂度的系数

• 结构风险最小化
  • 添加 regularization（正则化），调节损失函数（目标函数）
• 模型复杂度 $J(f)$ 表示对复杂模型的惩罚：模型 $f$ 越复杂，复杂项 $J(f)$ 越大
• 案例
  • maximum posterior probability estimation：最大后验概率估计
    • 损失函数：对数损失函数
    • 模型复杂度：模型先验概率对数后取负
    • 先验概率对应模型复杂度，先验概率越小，复杂度越大
  • 岭回归：平方损失 + $L2$ 正则化 $\mathop{\arg\min}{\beta} \sum_{i=1}^N (y_i - f(x_i, \beta))^2 + |\beta|$
  • LASSO：平方损失 + $L1$ 正则化 $\mathop{\arg\min}{\beta} \sum_{i=1}^N (y_i - f(x_i, \beta))^2 + |\beta|_1$

Generalization Ability

泛化能力：方法学习到的模型对未知数据的预测能力，是学习方法本质、重要的性质

• 测试误差衡量学习方法的泛化能力不可靠，其依赖于测试集，而测试集有限
• 学习方法的泛化能力往往是通过研究泛化误差的概率上界进行

Generalization Error Bound

泛化误差上界：泛化误差的 概率 上界

• 是样本容量函数，样本容量增加时，泛化上界趋于 0
• 是假设空间容量函数，假设空间容量越大，模型越难学习，泛化误差上界越大

泛化误差

• 根据 Hoeffding 不等式，泛化误差满足

  $$\begin{align*} & \forall h \in H, & P(|E(h) - \hat E(h)| \geq \epsilon) \leq 2 e^{-2 N \epsilon^2} \\ \Rightarrow & \forall h \in H, & P(|E(h) - \hat E(h)| \leq \epsilon) \geq 1 - 2|H|e^{-2N\epsilon^2} \end{align*}$$

  • $H$：假设空间
  • $N$：样本数量
  • $E(h) := R_{exp}(h)$
  • $\hat E(h) := R_{emp}(h)$

• 证明如下：

  $$\begin{align*} P(\forall h \in H: |E(h) - \hat E(h)| \leq \epsilon|) & = 1 - P(\exists h \in H: |E(h) - \hat E(h)| \geq \epsilon) \\ & = 1 - P((|E(h_1) - \hat E(h_1) \geq \epsilon) \vee \cdots \vee (|E(h_{|H|}) - \hat E_{|H|}| \geq \epsilon)) \\ & \geq 1 - \sum_{i=1}^{|H|} P(|E(h_i) - \hat E(h_i)| \geq \epsilon) \\ & \geq 1 - 2|H|e^{-2N \epsilon^2} \end{align*}$$

• 对任意 $\epsilon$，随样本数量 $m$ 增大， $|E(h) - \hat E(h)| \leq \epsilon$ 概率增大，可以使用经验误差近似泛化误差

二分类泛化误差上界

• 由 Hoeffding 不等式

  $$\begin{align*} P(E(h) - \hat E(h) & \geq \epsilon) \leq exp(-2N\epsilon^2) \\ P(\exists h \in H: E(h) - \hat E(h) \geq \epsilon) & = P(\bigcup_{h \in H} \{ E(h) - \hat E(h) \geq \epsilon \}) \\ & \leq \sum_{h \in H} P(E(h) - \hat E(h) \geq \epsilon) \\ & \leq |H| exp(-2 N \epsilon^2) \end{align*}$$

• 则 $\forall h \in H$，有

  $$P(E(h) - \hat E(h) < \epsilon) \geq 1 - |H| exp(-2 N \epsilon)$$

  则令 $\sigma = |H| exp(-2N\epsilon^2)$，则至少以概率 $1-\sigma$ 满足如下，即得到泛化误差上界

  $$\begin{align*} E(h) & \leq \hat E(h) + \epsilon(|H|, N, \sigma) \\ \epsilon(|H|, N, \sigma) & = \sqrt {\frac 1 {2N} (log |H| + log \frac 1 {\sigma})} \end{align*}$$

Probably Approximate Correct 可学习

PAC 可学习：在短时间内利用少量（多项式级别）样本能够找到假设 $h^{‘}$，满足

• 即需要假设满足两个 PAC 辨识条件

  • 近似条件：泛化误差 $E(h^{‘})$ 足够小
  • 可能正确：满足近似条件概率足够大

• 同等条件下

  • 模型越复杂，泛化误差越大
  • 满足条件的样本数量越大，模型泛化误差越小

• PAC 学习理论关心能否从假设空间 $H$ 中学习到好的假设 $h$

  • 由以上泛化误差可得，取 $\sigma = 2|H|e^{-2N\epsilon^2}$，则样本量满足 $N = \frac {ln \frac {2|H|} \sigma} {2 \epsilon^2}$ 时，模型是 PAC 可学习的

Regularization

正则化：（向目标函数）添加额外信息以求解病态问题、避免过拟合

• 常应用在机器学习、逆问题求解

  • 对模型（目标函数）复杂度惩罚
  • 提高学习模型的泛化能力、避免过拟合
  • 学习简单模型：稀疏模型、引入组结构

• 有多种用途

  • 最小二乘也可以看作是简单的正则化
  • 岭回归中的 $\mathcal{l_2}$ 范数

模型复杂度

模型复杂度：经常作为正则化项添加作为额外信息添加的，衡量模型复杂度方式有很多种

• 函数光滑限制

  • 多项式最高次数

• 向量空间范数

  • $\mathcal{L_0} - norm$：参数个数
  • $\mathcal{L_1} - norm$：参数绝对值和
  • $\mathcal{L_2}$- norm$：参数平方和

$\mathcal{L_0} - norm$

• $\mathcal{l_0} - norm$ 特点
  • 稀疏化约束
  • 解 $\mathcal{L_0}$ 范数正则化是 NP-hard 问题

$\mathcal{L_1} - norm$

• $\mathcal{L_1} - norm$ 特点

  • $\mathcal{L_1}$ 范数可以通过凸松弛得到 $\mathcal{L_0}$ 的近似解
  • 有时候出现解不唯一的情况
  • $\mathcal{L_1}$ 范数凸但不严格可导，可以使用依赖次梯度的方法求解极小化问题

• 应用

  • LASSO

• 求解

  • Proximal Method
  • LARS

$\mathcal{L_2} - norm$

• $\mathcal{L_2} - norm$ 特点
  • 凸且严格可导，极小化问题有解析解

$\mathcal{L_1 + L_2}$

• $\mathcal{L_1 + L_2}$ 特点

  • 有组效应，相关变量权重倾向于相同

• 应用

  • Elastic Net

稀疏解产生

稀疏解：待估参数系数在某些分量上为 0

$\mathcal{L_1} - norm$ 稀疏解的产生

• $\mathcal{L_1}$ 范数在参数满足 一定条件 情况下，能对 平方损失 产生稀疏效果

• 在 $[-1,1]$ 内 $y=|x|$ 导数大于 $y=x^2$（除 0 点）

  • 则特征在 0 点附近内变动时，为了取到极小值，参数必须始终为 0
  • 高阶项在 0 点附近增加速度较慢，所以 $\mathcal{L_1} - norm$ 能产生稀疏解是很广泛的
  • $mathcal{L_1} - norm$ 前系数（权重）越大，能够容许高阶项增加的幅度越大，即压缩能力越强

• 在 0 附近导数 “不小”，即导数在 0 点非 0

  • 对多项式正则化项
    • $\mathcal{L_1} - norm$ 项对稀疏化解起决定性作用
    • 其他项对稀疏解无帮助
  • 对“非多项式”正则化项
    • $e^{|x|}-1$、$ln(|x|+1)$ 等在0点泰勒展开同样得到 $\mathcal{L_1} - norm$ 项
    • 但是此类正则化项难以计算数值，不常用

$\mathcal{L_1} - norm$ 稀疏解推广

• 正负差异化：在正负设置权重不同的 $\mathcal{L_1}$，赋予在正负不同的压缩能力，甚至某侧完全不压缩

• 分段函数压缩：即只要保证在 0 点附近包含 $\mathcal{L_1}$ 用于产生稀疏解，远离 0 处可以设计为常数等不影响精确解的值

  • Smoothly Clipped Absolute Deviation

    $$R(x|\lambda, \gamma) = \left \{ \begin{array} {l} \lambda|x| \qquad & if |x| \leq \lambda \\ \frac {2\gamma\lambda|x| - x^2 - {\lambda}^2 } {2(\gamma - 1)} & if \gamma< |x| <\gamma\lambda \\ \frac { {\lambda}^2(\gamma+1)} 2 & if |x| \geq \gamma\lambda \end{array} \right.$$

  • Derivate of SCAD

    $$R(x; \lambda, \gamma) = \left \{ \begin{array} {l} \lambda \qquad & if |x| \leq \gamma \\ \frac {\gamma\lambda - |x|} {\gamma - 1} & if \lambda < |x| < \gamma\lambda \\ 0 & if |x| \geq \gamma\lambda \end{array} \right.$$

  • Minimax Concave Penalty

    $$R_{\gamma}(x;\lambda) = \left \{ \begin{array} {l} \lambda|x| - \frac {x^2} {2\gamma} \qquad & if |x| \leq \gamma\lambda \\ \frac 1 2 \gamma{\lambda}^2 & if |x| > \gamma\lambda \end{array} \right.$$

• 分指标：对不同指标动态设置 $\mathcal{L_0}$ 系数

  • Adaptive Lasso：$\lambda \sum_J w_jx_j$

稀疏本质

稀疏本质：极值、不光滑，即导数符号突然变化

• 若某约束项导数符号突然变化、其余项在该点处导数为 0，为保证仍然取得极小值，解会聚集（极小）、疏远（极大）该点（类似坡的陡峭程度）

  • 即此类不光滑点会抑制解的变化，不光滑程度即导数变化幅度越大，抑制解变化能力越强，即吸引、排斥解能力越强
  • 容易构造压缩至任意点的约束项
  • 特殊的，不光滑点为 0 时，即得到稀疏解

• 可以设置的多个极小不光滑点，使得解都在不连续集合中

  • 可以使用三角函数、锯齿函数等构造，但此类约束项要起效果，必然会使得目标函数非凸
    • 但是多变量场合，每个变量实际解只会在某个候选解附近，其邻域内仍然是凸的
    • 且锯齿函数这样的突变非凸可能和凸函数具有相当的优秀性质
  • 当这些点均为整数时，这似乎可以近似求解 整数规划

Early Stopping

Early Stopping：提前终止（训练）

• Early Stopping 也可以被视为是 regularizing on time
  • 迭代式训练随着迭代次数增加，往往会有学习复杂模型的倾向
  • 对时间施加正则化，可以减小模型复杂度、提高泛化能力

评估方向

模型误差

• 给定损失函数时，基于损失函数的误差显然评估学习方法的标准

• 回归预测模型：模型误差主要使用 MSE
• 分类预测模型：模型误差主要是分类错误率 ERR=1-ACC

• 模型训练时采用损失函数不一定是评估时使用的

Training Error

训练误差：模型在训练集上的误差，损失函数 $L(Y, F(X))$ 均值

• $\hat f$：学习到的模型
• $N$：训练样本容量

• 训练时采用的损失函数和评估时一致时，训练误差等于经验风险
• 训练误差对盘对给定问题是否容易学习是有意义的，但是本质上不重要
  • 模型训练本身就以最小化训练误差为标准，如：最小化 MSE、最大化预测准确率，一般偏低，不能作为模型预测误差的估计
  • 训练误差随模型复杂度增加单调下降（不考虑模型中随机因素）

Test Error

测试误差：模型在测试集上的误差，损失函数 $L(Y, f(X))$ 均值

• $\hat f$：学习到的模型
• $N$：测试样本容量

• 测试误差反映了学习方法对未知测试数据集的预测能力，是模型 generalization ability 的度量，可以作为模型误差估计

• 测试误差随模型复杂度增加呈U型

  • 偏差降低程度大于方差增加程度，测试误差降低
  • 偏差降低程度小于方差增加程度，测试误差增大
• 训练误差小但测试误差大表明模型过拟合，使测试误差最小的模型为理想模型

模型复杂度

• approximation error：近似误差，模型偏差，代表模型对训练集的拟合程度
• estimation error：估计误差，模型方差，代表模型对训练集波动的稳健性

• 模型复杂度越高

  • 低偏差：对训练集的拟合充分
  • 高方差：模型紧跟特定数据点，受其影响较大，预测结果不稳定
  • 远离真实关系，模型在来自同系统中其他尚未观测的数据集上预测误差大

• 而训练集、测试集往往不完全相同

  • 复杂度较高的模型（过拟合）在测试集上往往由于其高方差效果不好，而建立模型最终目的是用于预测未知数据
  • 所以要兼顾偏差和方差，通过不同建模策略，找到恰当模型，其复杂度不太大且误差在可接受的水平
  • 使得模型更贴近真实关系，泛化能力较好

• 简单模型：低方差高偏差

• 复杂模型：低偏差高方差

• 模型复杂度衡量参data_science/loss

Over-Fitting

过拟合：学习时选择的所包含的模型复杂度大（参数过多），导致模型对已知数据预测很好，对未知数据预测效果很差

• 若在假设空间中存在“真模型”，则选择的模型应该逼近真模型（参数个数相近）
• 一味追求对训练集的预测能力，复杂度往往会比“真模型”更高

解决方法

• 减少预测变量数量
  • 最优子集回归：选择合适评价函数（带罚）选择最优模型
  • 验证集挑选模型：将训练集使用 抽样技术 分出部分作为 validation set，使用额外验证集挑选使得损失最小的模型
  • 正则化（罚、结构化风险最小策略）
    • 岭回归：平方损失，$L_2$ 范数
    • LASSO：绝对值损失，$L_1$ 范数
    • Elastic Net
• 减弱变量特化程度：仅适合迭代求参数的方法
  • EarlyStop：提前终止模型训练
  • Dropout：每次训练部分神经元

模型信息来源

• 训练数据包含信息
• 模型形成过程中提供的先验信息
  • 模型：采用特定内在结构（如深度学习不同网络结构）、条件假设、其他约束条件（正则项）
  • 数据：调整、变换、扩展训练数据，让其展现更多、更有用的信息

评价指标

• Classification 分类问题：输出变量$Y$为有限个离散变量

  • 混淆矩阵
    • F-Measure
    • TPR、FPR
  • ROC
  • AUC

• Tagging 标注问题：输入 $X^{(1)}, X^{(2)}, \cdots, X^{(n)}$、输出 $Y^{(1)}, Y^{(2)}, \cdots, Y^{(n)}$ 均为变量序列

  • 类似分类问题

• Regression 回归问题

  • Squared Error
    • MSE
    • $R^2$、$R^2_{Adj}$
    • AIC
    • BIC
  • Absolute Error
    • MAE
    • MAPE
    • SMAPE

• 经验损失、结构损失总是能用作评价模型，但是意义不明确

损失函数

• 损失函数可以视为模型与真实的距离的度量
  • 因此损失函数设计关键即，寻找可以代表模型与真实的距离的统计量
  • 同时为求解方便，应该损失函数最好应满足导数存在

Surrogate Loss

代理损失函数：用优化方便的损失函数代替难以优化的损失函数，间接达到优化原损失函数的目标

• 如 0-1 损失难以优化，考虑使用二次损失、交叉熵损失替代

损失函数设计

• 对有监督学习：真实 已知，可以直接设计损失函数

• 对无监督学习：真实 未知，需要给定 真实标准

  • NLP：需要给出语言模型
  • EM 算法：熵最大原理

常用损失函数

0-1 Loss

• 0-1 损失函数梯度要么为 0、要么不存在，无法通过梯度下降方法优化 0-1 损失

• 适用场合

  • 二分类：Adaboost
  • 多分类：Adaboost.M1

Quadratic / Squared Error Loss

• 平方错误损失函数可导，可以基于梯度下降算法优化损失函数

• 适用场合

  • 回归预测：线性回归
  • 分类预测：0-1 二分类（根据预测得分、阈值划分）

Logistic SE

• 平方损失用于二分类时存在如下问题（模型输出无限制）

  • 若模型对某样本非常确信为正例，给出大于1预测值
  • 此时模型会进行不必要、开销较大的优化

• 考虑对模型输出进行 sigmoid 变换后作为预测值，再应用平方错误损失函数

  $$L(y, f(x)) = \frac 1 2 (y - \sigma(f(x)))^2$$
  • Logistic SE 损失函数曲线对 0-1 损失拟合优于平方损失
  • 但负区间存在饱和问题，损失最大只有 0.5

Cross Entropy

交叉熵损失

• $y$：样本实际值
• $f(x)$：各类别预测概率
• $K$：分类数目

• 交叉熵损失综合二次损失、logistic SE 优势，以正样本为例

  • 预测值较大时：损失接近 0，避免无效优化
  • 预测值较小时：损失偏导趋近于 -1，不会出现饱和现象

• $y$ 为 one-hot 编码时实际值时

  • 分类问题仅某分量为 1：此时交叉熵损失同对数损失（负对数极大似然函数）
  • 标签问题则可有分量为 1

• 适合场合

  • 多分类问题
  • 标签问题

Hinge Loss

• $y \in {-1, +1}$

• 合页损失函数：0-1 损失函数的上界，效果类似交叉熵损失函数

  • 要求分类不仅正确，还要求确信度足够高损失才为 0
  • 即对学习有更高的要求

• 适用场合

  • 二分类：线性支持向量机

收敛速度对比

• 指数激活函数时：相较于二次损失，收敛速度更快

• 二次损失对 $w$ 偏导

  $$\frac {\partial L} {\partial w} = (\sigma(z) - y) \sigma^{'}(z) x$$

  • $\sigma$：sigmoid、softmax 激活函数
  • $z = wx + b$

  • 考虑到 sigmoid 函数输入值绝对值较大时，其导数较小
  • 激活函数输入 $z=wx+b$ 较大时，$\sigma^{‘}(z)$ 较小，更新速率较慢

• Softmax 激活函数时，交叉熵对 $w$ 偏导

  $$\begin{align*} \frac {\partial L} {\partial w} & = -y\frac 1 {\sigma(z)} \sigma^{'}(z) x \\ & = y(\sigma(z) - 1)x \end{align*}$$

• 特别的，对 sigmoid 二分类

  $$\begin{align*} \frac {\partial L} {\partial w_j} & = -(\frac y {\sigma(z)} - \frac {(1-y)} {1-\sigma(z)}) \sigma^{'}(z) x \\ & = -\frac {\sigma^{'}(z) x} {\sigma(z)(1-\sigma(z))} (\sigma(z) - y) \\ & = x(\sigma(z) - y) \end{align*}$$
  • 考虑 $y \in {(0,1), (1,0)}$、$w$ 有两组
  • 带入一般形式多分类也可以得到二分类结果

不常用损失函数

Absolute Loss

绝对损失函数

• 适用场合
  • 回归预测

Logarithmic Loss

对数损失函数（负对数极大似然损失函数）

• 适用场合
  • 多分类：贝叶斯生成模型、逻辑回归

Exponential Loss

指数函数函数

• 适用场合
  • 二分类：前向分步算法

Pseudo Loss

伪损失：考虑个体损失 $(x_i, y_i)$ 如下，据此构造伪损失

• $h(x_i, y_i)=1, \sum h(x_i, y)=0$：完全正确预测
• $h(x_i, y_i)=0, \sum h(x_i, y)=1$：完全错误预测
• $h(x_i, y_i)=1/M$：随机预测（M为分类数目）

• $w_j$：样本个体错误标签权重，对不同个体分布可不同
• $f(x, y^{(j)})$：分类器将输入 $x$ 预测为第 $j$ 类 $y^{(j)}$ 的置信度

• 伪损失函数考虑了预测 标签 的权重分布

  • 通过改变此分布，能够更明确的关注难以预测的个体标签，而不仅仅个体

• 伪损失随着分类器预测准确率增加而减小

  • 分类器 $f$ 对所有可能类别输出置信度相同时，伪损失最大达到 0.5，此时就是随机预测
  • 伪损失大于 0.5 时，应该将使用 $1-f$

• 适用场景

  • 多分类：Adaboost.M2

Stacked Generalization

堆栈泛化：使用多种模型分别训练训练，将其结果叠加作为下层 模型的输入，最终得到预测输出

• 属于异源集成模型，可以视为

  • 复合函数

    

  • 短路网络

    

• 从某种意义上，复杂模型都是stacking

思想

• 不同模型侧重于获取数据不同方面的特征

  • 使用基学习器抽取数据特征进行表示学习，提取不同角度的 数据高维特征
  • 考虑到使用全量训练数据训练、预测作为下层模型输入会 导致过拟合，可使用K折交叉验证避免过拟合
  • 有些基学习器只使用适合其部分特征训练
    • GBDT、DNN适合低维稠密特征

• 元学习器组合多个基学习器的输出

  • 从数据高维特征学习数据模式，具有更好的泛化能力，避免 过拟合

算法

• 输入：模型$M1, M_2, \cdots, M_d$、训练特征：$X{n*m}$、 训练标签$Y_{n}$、测试特征$X^{‘}$
• 输出：stacking模型、预测标签

• 将训练数据K折划分，对第$i$轮划分

  • 使用模型$M1, M_2, \cdots, M_d$分别在相应训练集 $[X[:n_i,:], X[n{i+1}:,:]]$、 $[Y[:ni], Y[n{i+1}:]]$上训练
  • 在相应验证集$X[ni:n{i+1}, :]$上验证、并记录验证 结果
  • 将验证集验证结果叠加得到部分样本新特征 $N[ni: n{i+1}, d]$

• 将K轮划分得到的部分新特征拼接得到训练集的完整新特征 $N_{n * d}$，将新特征作为输入，训练下层模型，得到最终 stacking模型

• 将测试特征如上作为输入经过两层模型预测，得到最终预测结果

• 以上以2层stacking为例，有深层stacking

常用模型

基学习器

• 交叉项、原始特征本身也可以视为线性基学习器学习到的特征

• 具体模型参见 ml_specification/rec_system/ctr_stacking_models

GBDT

• 各树中各节点对应元学习器一维输入特征

• 适合低维稠密通用特征，对输入特征分布没有要求

• GBDT树根据熵增益（Gini系数增益）划分节点，每条路径 都代表一定区分能力

  • 以叶子节点（路径）作为特征，相当于自动进行特征 转换、组合、选择、离散化，得到高维组合特征

• GDBT相较于单棵树、或RF更适合stacking

  • 单棵树表达能力弱，无法表达多个有区分性特征组合， 集成模型可将样本映射为多个特征
  • GBDT拟合残差意味着各树对样本区分度不同，对各特征 区别对待更合理

DNN

• 适合普通稠密特征、embedding特征
• 模型表达能力强，能抽取有良好分布数据的深层次特征，提高 模型准确性、泛化能力
• 容易扩充其他类别特征，如：图片、文字

元学习器

• LR

  • 适合低维稀疏特征，可对所有特征离散化以引入非线性

• FM

  • 适合低维稀疏特征
  • LR基础上自动组合二阶交叉项

• Linear：训练模型、对训练结果线性加权

?

Emsemble Learning

• 集成学习：训练多个基模型，并将其组合起来，以达到更好的 预测能力、泛化能力、稳健性
• base learner：基模型，基于独立样本建立的、一组 具有相同形式的模型中的一个
• 组合预测模型：由基模型组合，即集成学习最终习得模型

• 源于样本均值抽样分布思路

  • $var(\bar{X}) = \sigma^2 / n$
  • 基于独立样本，建立一组具有相同形式的基模型
  • 预测由这组模型共同参与
  • 组合预测模型稳健性更高，类似于样本均值抽样分布方差 更小

• 关键在于

  • 获得多个独立样本的方法
  • 组合多个模型的方法

分类

• homogenous ensemble：同源集成，基学习器属于同一类型

  • bagging
  • boosting

• heterogenous ensemble：异源集成，基学习器不一定属于同 一类型

  • [genralization] stacking

• 以上都是指原始版本、主要用途

Boosting

提升方法：将弱可学习算法提升为强可学习算法的组合元算法

• 属于加法模型：即基函数的线性组合
• 各模型之间存在依赖关系

分类Boosting

• 依次学习多个基分类器
• 每个基分类器依之前分类结果调整权重
• 堆叠多个分类器提高分类准确率

• boosting通过组合多个误分率略好于随机猜测的分类器得到 误分率较小的分类器，因此boosting适合这两类问题

  • 个体之间难度有很大不同，boosting能够更加关注较难的 个体
  • 学习器对训练集敏感，boosting驱使学习器在趋同的、 “较难”的分布上学习，此时boosting就和bagging一样能够 使得模型更加稳健（但原理不同）

• boosting能减小预测方差、偏差、过拟合

  • 直觉上，使用在不同的样本上训练的基学习器加权组合， 本身就能减小学习器的随机变动

  • 基于同样的理由，boosting同时也能减小偏差

  • 过拟合对集成学习有些时候有正面效果，其带来多样性， 使模型泛化能力更好，前提是样本两足够大，否则小样本 仍然无法提供多样性

回归Boosting

• 依次训练多个基学习器
• 每个基学习器以之前学习器拟合残差为目标
• 堆叠多个学习器减少整体损失

• boosting组合模型整体损失（结构化风险）

  $$R_{srm} = \sum_{i=1}^N l(y_i, \hat y_i) + \sum_{t=1}^M \Omega(f_t)$$

  • $l$：损失函数
  • $f_t$：基学习器
  • $\Omega(f_t)$：单个基学习器的复杂度罚
  • $N, M$：样本数目、学习器数目

• 基学习器损失

  $$obj^{(t)} = \sum_{i=1}^N l(y_i, \hat y_i^{(t)}) + \Omega(f_t)$$

最速下降法

使用线性函数拟合$l(y_i, \hat y_i^{(t)})$

• $gi = \partial{\hat y} l(y_i, \hat y^{t-1})$

• 一次函数没有极值
• 将所有样本损失视为向量（学习器权重整体施加），则负梯度 方向损失下降最快，考虑使用负梯度作为伪残差

Newton法

使用二次函数拟合$l(y_i, \hat y_i^{(t)}$

• $hi = \partial^2{\hat y} l(y_i, \hat y^{t-1})$

• 二次函数本身有极值
• 可以结合复杂度罚综合考虑，使得每个基学习器损失达到最小

Boosting&Bagging

• 基分类器足够简单时，boosting表现均显著好于bagging

  • 仅靠单次决策（单个属性、属性组合）分类

• 使用C4.5树作为基分类器时，boosting仍然具有优势，但是不够 有说服力

• 结论来自于Experiments with a New Boosting Algorithm

Boosting&Bagging

• 基分类器足够简单时，boosting表现均显著好于bagging

  • 仅靠单次决策（单个属性、属性组合）分类

• 使用C4.5树作为基分类器时，boosting仍然具有优势，但是不够 有说服力

• 结论来自于Experiments with a New Boosting Algorithm

原理

probably approximately correct：概率近似正确，在概率近似 正确学习的框架中

• strongly learnable：强可学习，一个概念（类），如果存在 一个多项式的学习算法能够学习它，并且正确率很高，那么 就称为这个概念是强可学习的

• weakly learnable：弱可学习，一个概念（类），如果存在 一个多项式的学习算法能够学习它，学习的正确率仅比随机猜测 略好，称此概念为弱可学习的

• Schapire证明：在PAC框架下强可学习和弱可学习是等价的

具体措施

• 弱学习算法要比强学习算法更容易寻找，所以具体实施提升就是 需要解决的问题

• 改变训练数据权值、概率分布的方法

  • 提高分类错误样本权值、降低分类正确样本权值

• 将弱学习器组合成强学习器的方法

  • competeing
  • simple majority voting
  • weighted majority voting
  • confidence-based weighting

学习器组合方式

• 很多模型无法直接组合，只能组合预测结果

• simple majority voting/simple average：简单平均

  $$h = \frac 1 K \sum_{k=1}_K h_k$$

  • $h_k$：第k个预测

• weighted majority voting/weighted average：加权平均

  $$h = \frac {\sum_{k=1}^K w_k h_k} {\sum_{k=1}^K w_k}$$

  • $w_k$：第k个预测权重，对分类器可以是准确率

• competing voting/largest：使用效果最优者

• confidence based weighted：基于置信度加权

  $$\begin{align*} h = \arg\max_{y \in Y} \sum_{k=1}^K ln(\frac {1 - e_k} {e_k}) h_k \end{align*}$$

  • $e_k$：第k个模型损失

Meta Learning

元学习：自动学习关于关于机器学习的元数据的机器学习子领域

• 元学习主要目标：使用学习到元数据解释，自动学习如何 flexible的解决学习问题，借此提升现有学习算法性能、 学习新的学习算法，即学习学习

• 学习算法灵活性即可迁移性，非常重要

  • 学习算法往往基于某个具体、假象的数据集，有偏
  • 学习问题、学习算法有效性之间的关系没有完全明白，对 学习算法的应用有极大限制

要素

• 元学习系统必须包含子学习系统
• 学习经验通过提取元知识获得经验，元知识可以在先前单个 数据集，或不同的领域中获得
• 学习bias（影响用于模型选择的前提）必须动态选择
  • declarative bias：声明性偏见，确定假设空间的形式 ，影响搜索空间的大小
    • 如：只允许线性模型
  • procedural bias：过程性偏见，确定模型的优先级
    • 如：简单模型更好

Recurrent Neural networks

RNN：self-referential RNN理论上可以通过反向传播学习到， 和反向传播完全不同的权值调整算法

Meta Reinforcement Learning

MetaRL：RL智能体目标是最大化奖励，其通过不断提升自己的学习 算法来加速获取奖励，这也涉及到自我指涉

Additional Model

加法模型：将模型视为多个基模型加和而来

• $b(x;\theta_m)$：基函数
• $\theta_m$：基函数的参数
• $\beta_m$：基函数的系数

• 则相应风险极小化策略

  $$\arg\min_{\beta_m, \theta_m} \sum_{i=1}^N L(y_i, \sum_{m=1}^M \beta_m b(x_i;\theta_m))$$

  • $L(y, f(x))$：损失函数

Forward Stagewise Algorithm

前向分步算法：从前往后，每步只学习加法模型中一个基函数 及其系数，逐步逼近优化目标函数，简化优化复杂度

• 即每步只求解优化

  $$\arg\min_{\beta, \theta} \sum_{i=1}^N L(y_i, \hat f_m(x_i) + \beta b(x_i;\theta))$$

  • $\hat f_m$：前m轮基函数预测值加和

步骤

• 输入：训练数据集$T={(x_1,y_1), \cdots, (x_N,y_N)}$，损失 函数$L(y,f(x))$，基函数集${b(x;\theta)}$
• 输出：加法模型$f(x)$

• 初始化$f_0(x)=0$

• 对$m=1,2,\cdots,M$，加法模型中M个基函数

  • 极小化损失函数得到参数$\beta_m, \theta_m$

    $$(\beta_m, \theta_m) = \arg\min_{\beta, \theta} \sum_{i=1}^N L(y_i, f_{m-1}(x_1) + \beta b(x_i; \theta))$$

  • 更新

    $$f_m(x) = f_{m-1}(x) + \beta_m b(x;y_M)$$

• 得到加法模型

  $$f(x) = f_M(x) = \sum_{i=1}^M \beta_m b(x;\theta_m)$$

AdaBoost&前向分步算法

AdaBoost（基分类器loss使用分类误差率）是前向分步算法的特例， 是由基本分类器组成的加法模型，损失函数是指数函数

• 基函数为基本分类器时加法模型等价于AdaBoost的最终分类器 $f(x) = \sum_{m=1}^M \alpha_m G_m(x)$

• 前向分步算法的损失函数为指数函数$L(y,f(x))=exp(-yf(x))$ 时，学习的具体操作等价于AdaBoost算法具体操作

  • 假设经过m-1轮迭代，前向分步算法已经得到

    $$\begin{align*} f_{m-1}(x) & = f_{m-2}(x) + \alpha_{m-1}G_{m-1}(x) \\ & = \alpha_1G_1(x) + \cdots + \alpha_{m-1}G_{m-1}(x) \end{align*}$$

  • 经过第m迭代得到$\alpha_m, G_m(x), f_m(x)$，其中

    $$\begin{align*} (\alpha_m, G_m(x)) & = \arg\min_{\alpha, G} \sum_{i=1}^N exp(-y_i(f_{m-1}(x_i) + \alpha G(x_i))) \\ & = \arg\min_{\alpha, G} \sum_{i=1}^N \bar w_{m,i} exp(-y_i \alpha G(x_i)) \end{align*}$$

    • $\bar w{m,i}=exp(-y_i f{m-1}(x_i))$：不依赖 $\alpha, G$

  • $\forall \alpha > 0$，使得损失最小应该有 （提出$\alpha$）

    $$\begin{align*} G_m^{*}(x) & = \arg\min_G \sum_{i=1}^N \bar w_{m,i} exp(-y_i f_{m-1}(x_i)) \\ & = \arg\min_G \sum_{i=1}^N \bar w_{m,i} I(y_i \neq G(x_i)) \end{align*}$$

    此分类器$G_m^{*}$即为使得第m轮加权训练误差最小分类器 ，即AdaBoost算法的基本分类器

  • 又根据

    $$\begin{align*} \sum_{i=1}^N \bar w_{m,i} exp(-y_i \alpha G(x_i)) & = \sum_{y_i = G_m(x_i)} \bar w_{m,i} e^{-\alpha} + \sum_{y_i \neq G_m(x_i)} \bar w_{m,i} e^\alpha \\ & = (e^\alpha - e^{-\alpha}) \sum_{i=1}^N (\bar w_{m,i} I(y_i \neq G(x_i))) + e^{-\alpha} \sum_{i=1}^N \bar w_{m,i} \end{align*}$$

    带入$G_m^{*}$，对$\alpha$求导置0，求得极小值为

    $$\begin{align*} \alpha_m^{*} & = \frac 1 2 log \frac {1-e_m} {e_m} \\ e_m & = \frac {\sum_{i=1}^N (\bar w_{m,i} I(y_i \neq G_m(x_i)))} {\sum_{i=1}^N \bar w_{m,i}} \\ & = \frac {\sum_{i=1}^N (\bar w_{m,i} I(y_i \neq G_m(x_i)))} {Z_m} \\ & = \sum_{i=1}^N w_{m,i} I(y_i \neq G_m(x_i)) \end{align*}$$

    • $w_{m,i}, Z_M$同AdaBoost中

    即为AdaBoost中$\alpha_m$

  • 对权值更新有

    $$\bar w_{m+1,i} = \bar w_{m,i} exp(-y_i \alpha_m G_m(x))$$

    与AdaBoost权值更新只相差规范化因子$Z_M$

AdaBoost

通过改变训练样本权重，学习多个分类器，并将分类器进行线性 组合，提高分类性能

• 对离群点、奇异点敏感
• 对过拟合不敏感

Boosting实现

• 改变训练数据权值或概率分布：提高分类错误样本权值、降低 分类正确样本权值

• 弱分类器组合：加权多数表决，即加大分类误差率小的弱分类器 权值，使其在表决中起更大作用；减小分类误差率大的弱分类器 权值，使其在表决中起更小作用

步骤

• 输入：训练数据集$T={(x_1, y_1), \cdots, (x_N, y_N)}$， 弱分类器算法$G(x)$

  • $x_i \in \mathcal{X \subset R^n}$
  • $y_i \in \mathcal{Y} = {-1, +1 }$

• 输出：最终分类器$G(x)$

• 初始化训练数据权值分布： $D1=(w{11}, \cdots, w{1N}), w{1i}=\frac 1 N$

• 对$m=1,2,\cdots,M$（即训练M个弱分类器）

  • 使用具有权值分布$D_m$的训练数据学习，得到基本 分类器

    $$G_m(x):\mathcal{X} \rightarrow \{-1, +1\}$$

  • 计算$G_m(x)$在训练数据集上的分类误差率

    $$\begin{align*} e_m & = P(G_m(x_i)) \neq y_i) \\ & = \sum_{i=1}^N w_{mi}I(G_m(x_i) \neq y_i) \\ & = \sum_{G_m(x_i) \neq y_i} w_{mi} \end{align*}$$

  • 计算$G_m(x)$组合为最终分类器时权重

    $$\alpha = \frac 1 2 log \frac {1-e_m} {e_m}$$

    • $\alpha_m$表示就简单分类器$G_m(x)$在最终分类器中 的重要性，随$e_m$减小而增加 （弱分类器保证$e_m \leq 1/2$）

  • 更新训练集权值分布

    $$\begin{align*} D_{m+1} & = (w_{m+1,1}, \cdots, w_{m+1,N}) \\ w_{m+1,i} & = \frac {w_{mi}} {Z_m} exp(-\alpha y_i G_m(x_i)) = \left \{ \begin{array}{l} \frac {w_mi} {Z_m} e^{-\alpha_m}, & G_m(x_i) = y_i \\ \frac {w_mi} {Z_m} e^{\alpha_m}, & G_m(x_i) \neq y_i \\ \end{array} \right. \\ Z_m & = \sum_{i=1}^N w_{mi} exp(-\alpha_m y_i G_m(x_i)) \end{align*}$$

    • $Zm$：规范化因子，是第m轮调整后的权值之和，其 使得$D{m+1}$成为概率分布
    • 误分类样本权值相当于被放大 $e^{2\alpha_m} = \frac {e_m} {1 - e_m}$倍

• 构建基本分类器线性组合

  $$f(x) = \sum_{m=1}^M \alpha_m G_m(x)$$

  得到最终分类器

  $$G(x) = sign(f(x)) = sign(\sum_{m=1}^M \alpha_m G_m(x))$$

  • 这里$\alpha_m$没有规范化，和不为1，规范化没有必要
  • $f(x)$符号决定分类预测结果，绝对值大小表示分类确信度

• AdaBoost中分类器学习和之后的分类误差率“无关”，基分类器 学习算法中的loss不是分类误差率，可以是其他loss，只是需要 考虑训练数据的权值分布

  • 好像基学习器的loss就要是和集成部分调权的loss一致

    todo

  • 按权值分布有放回的抽样，在抽样集上进行训练
  • 各样本loss按权重加权，类似分类误差率中加权

训练误差边界

AdaBoost算法最终分类器的训练误差边界为

• $G(x_i) \neq y_i$时，$y_if(x_i)<0$，所以 $exp(-y_i f(x_i)) \geq 1$，则不等式部分可证

• $$\begin{align*} \frac 1 N \sum_i exp(-y_i f(x_i)) & = \frac 1 N \sum_i exp(-\sum_{m=1}^M \alpha_m y_i G_m(x_i)) \\ & = \sum_i (w_{1,i} \prod_{m=1}^M exp(-\alpha_m y_i G_m(x_i))) \\ & = \sum_i (Z_1 w_{2,i} \prod_{m=2}^M exp(-\alpha_m y_i G_m(x_i))) \\ & = \prod_{m=1}^M Z_i \sum_i w_{M+1,i} \\ & = \prod_{m=1}^M Z_i \end{align*}$$

• AdaBoost训练误差边界性质的关键：权重调整与基本分类器权重 调整共系数（形式不完全一样）
• 这也是AdaBoost权重调整设计的依据，方便给出误差上界

二分类训练误差边界

• $\gamma_m = \frac 1 2 - e_m$

• $$\begin{align*} Z_m & = \sum_{i=1}^N w_{m,i} exp(-\alpha y_i G_m(x_i)) \\ & = \sum_{y_i = G_m(x_i)} w_{m,i}e^{-\alpha_m} + \sum_{y_i \neq G_m(x_i)} w_{m,i}e^{\alpha_m} \\ & = (1-e_m)e^{-\alpha_m} + e_m e^{\alpha_m} \\ & = 2\sqrt{e_m(1-e_m)} \\ & = \sqrt{1-4\gamma^2} \end{align*}$$

• 由$\forall x \in [0, 0.5], e^{-x} > \sqrt{1-2x}$可得， $\sqrt{1-4\gamma_m^2} \leq exp(-2\gamma_m^2)$

• 二分类AdaBoost误差边界性质的关键：$\alpha$的取值，也是 前向分步算法（损失函数）要求
• 若存$\gamma > 0$，对所有m有$\gamma_m \geq \gamma$，则 $$\frac 1 N \sum_{i=1}^N I(G(x_i) \neq y_i) \neq exp(-2M\gamma^2)$$ 即AdaBoost的训练误差是指数下降的
• 分类器下界$\gamma$可以未知，AdaBoost能适应弱分类器各自 训练误差率，所以称为adptive

Adaboost.M1

Adaboost.M1是原版AdaBoost的多分类升级版，基本思想同Adaboost

Boosting实现

• 基分类器组合方式

  • 仍然是加权投票，且投票权重同Adaboost
  • 出于多分类考虑，没有使用sign符号函数

• 改变训练数据权值或概率分布：和Adaboost形式稍有不同，但 相对的错误分类样本提升比率完全相同

  • 被上个分类器错误分类样本，权值保持不变
  • 被上个分类器正确分类样本，权值缩小比例是Adaboost平方

步骤

• 输入

  • 训练集：$T={x_i, y_i}, i=1,\cdots,N; y_i \in C, C={c_1, \cdots, c_m}$
  • 训练轮数：T
  • 弱学习器：I

• 输出：提升分类器

  $$H(x) = \arg\max_{y \in C} \sum_{m=1}^M ln(\frac 1 {\beta_m}) [h_m(x) = y]$$

  • $h_t, h_t(x) \in C$：分类器
  • $\beta_t$：分类器权重

误分率上界

• 对弱学习算法产生的伪损失$\epsilon1,\cdots,\epsilon_t$， 记$\gamma_t = 1/2 \epsilon_t$，最终分类器$h{fin}$误分率 上界有 $$\frac 1 N |\{i: h_{fin}(x_i) \neq y_i \}| \leq \prod_{t-1}^T \sqrt {1-4\gamma^2} \leq exp(-2 \sum_{t-1}^T \gamma^2)$$

特点

Adaboost.M1和Adaboost基本上没有区别

• 类别数目为2的Adaboost.M1就是Adaboost
• 同样无法处理对误分率高于0.5的情况，甚至在多分类场合， 误分率小于0.5更加难以满足
• 理论误分率上界和Adaboost相同

Adaboost.M2

AdaboostM2是AdaboostM1的进阶版，更多的利用了基分类器信息

• 要求基学习器能够输出更多信息：输出对样本分别属于各类别 的置信度向量，而不仅仅是最终标签
• 要求基分类器更加精细衡量错误：使用伪损失代替误分率 作为损失函数

Psuedo-Loss

• $D$：权重分布（行和为1，但不满足列和为1）

  • $D_{i,y}$：个体$x_i$中错误标签$y$的权重，代表从个体 $x_i$中识别出错误标签$y$的重要性

• $B = {(i, y)|y \neq y_i, i=1,2,\cdots,N }$
• $w$：个体各错误标签权重边际分布
• $h(x, y)$：模型$h$预测样本$x$为$y$的置信度

  • $h(x_i,y_i)$：预测正确的置信度
  • $h(x_i,y), y \neq y_i$：预测$x_i$为错误分类$y$置信度

• 伪损失函数同时考虑了样本和标签的权重分布
• 通过改变此分布，能够更明确的关注难以预测的个体标签， 而不仅仅个体

Boosting实现

• 改变数据权值或者概率分布

  • 使用psuedo-loss替代误分率，以此为导向改变权值
  • 对多分类每个错误分类概率分别计算错误占比，在此基础上 分别计算

• 基分类器组合方式：同Adaboost.M1

步骤

训练误差上界

• 对弱学习算法产生的伪损失$\epsilon1,\cdots,\epsilon_t$， 记$\gamma_t = 1/2 \epsilon_t$，最终分类器$h{fin}$误分率 上界有

特点

• 基于伪损失的Adaboost.M2能够提升稍微好于随机预测的分类器

• Adaboosting.M2能够较好的解决基分类器对噪声的敏感性，但是 仍然距离理论最优Bayes Error有较大差距，额外误差主要 来自于

  • 训练数据
  • 过拟合
  • 泛化能力

• 控制权值可以有效的提升算法，减小最小训练误差、过拟合 、泛化能力

  • 如对权值使用原始样本比例作为先验加权

• 其分类结果不差于AdaBoost.M1（在某些基分类器、数据集下）

Bagging

bagging：bootstrap aggregating，每个分类器随机从原样本 中做有放回的随机抽样，在抽样结果上训练基模型，最后根据 多个基模型的预测结果产生最终结果

• 核心为bootstrap重抽样自举

步骤

• 建模阶段：通过boostrap技术获得k个自举样本 $S_1, S_2,…, S_K$，以其为基础建立k个相同类型模型 $T_1, T_2,…, T_K$

• 预测阶段：组合K个预测模型

  • 分类问题：K个预测模型“投票”
  • 回归问题：K个预测模型平均值

模型性质

• 相较于单个基学习器，Bagging的优势
  • 分类Bagging几乎是最优的贝叶斯分类器
  • 回归Bagging可以通过降低方差（主要）降低均方误差

预测误差

总有部分观测未参与建模，预测误差估计偏乐观

• OOB预测误差：out of bag，基于袋外观测的预测误差， 对每个模型，使用没有参与建立模型的样本进行预测，计算预测 误差

• OOB观测比率：样本总量n较大时有

  $$r = (1 - \frac 1 n)^n \approx \frac 1 e = 0.367$$
  • 每次训练样本比率小于10交叉验证的90%

Random Forest

随机森林：随机建立多个有较高预测精度、弱相关（甚至不相关） 的决策树（基础学习器），多棵决策树共同对新观测做预测

• RF是Bagging的扩展变体，在以决策树为基学习器构建Bagging 集成模型的基础上，在训练过程中引入了随机特征选择

• 适合场景

  • 数据维度相对较低、同时对准确率有要求
  • 无需很多参数调整即可达到不错的效果

步骤

• 样本随机：Bootstrap自举样本

• 输入属性随机：对第i棵决策树通过随机方式选取K个输入变量 构成候选变量子集$\Theta_I$

  • Forest-Random Input：随机选择$k=log_2P+1或k=\sqrt P$ 个变量

  • Forest-Random Combination

    • 随机选择L个输入变量x
    • 生成L个服从均匀分布的随机数$\alpha$
    • 做线性组合 $vj = \sum{i=1}^L \alpha_i x_i, \alpha_i \in [-1, 1]$
    • 得到k个由新变量v组成的输入变量子集$\Theta_i$

• 在候选变量子集中选择最优变量构建决策树

  • 生成决策树时不需要剪枝

• 重复以上步骤构建k棵决策树，用一定集成策略组合多个决策树

  • 简单平均/随机森林投票

优点

• 样本抽样、属性抽样引入随机性

  • 基学习器估计误差较大，但是组合模型偏差被修正
  • 不容易发生过拟合、对随机波动稳健性较好
  • 一定程度上避免贪心算法带来的局部最优局限

• 数据兼容性

  • 能够方便处理高维数据，“不用做特征选择”
  • 能处理分类型、连续型数据

• 训练速度快、容易实现并行

• 其他

  • 可以得到变量重要性排序
  • 启发式操作
  • 优化操作

缺点

• 决策树数量过多时，训练需要资源多
• 模型解释能力差，有点黑盒模型

Gredient Boosting

GB：（利用）梯度提升，将提升问题视为优化问题，前向分步算法 利用最速下降思想实现

• 一阶展开拟合损失函数，沿负梯度方向迭代更新

  • 损失函数中，模型的样本预测值$f(x)$是因变量
  • 即$f(x)$应该沿着损失函数负梯度方向变化
  • 即下个基学习器应该以负梯度方向作为优化目标，即负梯度 作为伪残差

  • 类似复合函数求导

• 对基学习器预测值求解最优加权系数

  • 最速下降法中求解更新步长体现
  • 前向分布算法中求解基学习器权重

损失函数

基学习器拟合目标：损失函数的负梯度在当前模型的值

平方损失

平方损失：$L(y, f(x)) = \frac 1 2 (y - f(x))^2$（回归）

• 第m-1个基学习器伪残差为

  $$r_{m,i} = y_i - f_{m-1}(x_i), i=1,2,\cdots,N$$

  • $N$：样本数量

• 第m个基学习器为

  $$\begin{align*} h_m & = \arg\min_h \sum_{i=1}^N \frac 1 2 (y_i - (f_{m-1}(x_i) + h(x)))^2 \\ & = \arg\min_h \sum_{i=1}^N \frac 1 2 (C_{m,i} - h(x))^2 \\ C_{m,i} & = y_i - f_{m-1}(x_i) \end{align*}$$

• 第m轮学习器组合为

  $$f_m = f_{m-1} + \alpha_m h_m$$

  • $\alpha_m$：学习率，留给之后基模型学习空间

  • 这里只是形式上表示模型叠加，实际上树模型等不可加， 应该是模型预测结果叠加

指数损失

指数损失：$L(y, f(x)) = e^{-y f(x)}$（分类）

• 第m-1个基学习器伪残差

  $$r_{m,i} = -y_i e^{-y_i f_{m-1}(x_i)}, i=1,2,\cdots,N$$

• 基学习器、权重为

  $$\begin{align*} h_m & = \arg\min_h \sum_{i=1}^N exp(-y_i(f_{m-1}(x_i) + \alpha f(x_i))) \\ & = \arg\min_h \sum_{i=1}^N C_{m,i} exp(-y_i \alpha f(x_i)) \\ C_{m,i} & = exp(-y_i f_{m-1}(x_i)) \end{align*}$$

• 第m轮学习器组合为

  $$f_m = f_{m-1} + \alpha_m h_m$$

步骤

• 输入：训练数据集$T={(x_1, y_1), \cdots, (x_N, y_N)}$， 损失函数$L(y, f(x))$

  • $x_i \in \mathcal{X \subset R^n}$
  • $y_i \in \mathcal{Y} = {-1, +1 }$

• 输出：回归树$\hat f(x)$

• 初始化模型

  $$\hat y_i^{(0)} = \arg\min_{\hat y} \sum_{i=1}^N L(y_i, \hat y)$$

• 对$m=1,2,\cdots,M$（即训练M个若分类器）

  • 计算伪残差

    $$r_i^{(t)} = -\left [ \frac {\partial L(y, \hat y_i)} {\partial y_i} \right ]_{\hat y_i=\hat y_i^{(t-1)}}$$

  • 基于${(x_i, r_i^{(t)})}$生成基学习器$h_t(x)$

  • 计算最优系数

    $$\gamma = \arg\min_\gamma \sum_{i=1}^N L(y_i, \hat y_i^{(t-1)} + \gamma h_t(x_i))$$

  • 更新预测值

    $$\hat y_i^{(t)} = \hat y_i^{(t-1)} + \gamma_t h_t (x)$$

• 得到最终模型

  $$\hat f(x) = f_M(x) = \sum_{t=1}^M \gamma_t h_t(x)$$

Gradient Boosted Desicion Tree

GBDT：梯度提升树，以回归树为基学习器的梯度提升方法

• GBDT会累加所有树的结果，本质上是回归模型（毕竟梯度）

  • 所以一般使用CART回归树做基学习器
  • 当然可以实现分类效果

• 损失函数为平方损失（毕竟回归），则相应伪损失/残差

  $$r_{t,i} = y_i - f_{t-1}(x_i), i=1,2,\cdots,N$$

特点

• 准确率、效率相较于RF有一定提升
• 能够灵活的处理多类型数据
• Boosting类算法固有的基学习器之间存在依赖，难以并行训练 数据，比较可行的并行方案是在每轮选取最优特征切分时，并行 处理特征

XGBoost

Extreme Gradient Boost/Newton Boosting：前向分步算法利用 Newton法思想实现

• 二阶展开拟合损失函数

  • 损失函数中，模型的样本预测值$\hat y_i$是因变量
  • 将损失函数对$\hat y_i$二阶展开拟合
  • 求解使得损失函数最小参数

• 对基学习器预测值求解最优加权系数

  • 阻尼Newton法求解更新步长体现
  • 前向分布算法中求解基学习器权重
  • 削弱单个基学习器影响，让后续基学习器有更大学习空间

损失函数

• 第t个基分类器损失函数

  $$\begin{align*} obj^{(t)} & = \sum_{i=1}^N l(y_i, \hat y_i^{(t)}) + \Omega(f_t) \\ & = \sum_i^N l(y_i, \hat y_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) \\ & \approx \sum_{i=1}^N [l(y_i, \hat y^{(t-1)}) + g_i f_t(x_i) + \frac 1 2 h_i f_t^2(x_i)] + \Omega(f_t) \\ & = \sum_{i=1}^N [l(y_i, \hat y^{(t-1)}) + g_i f_t(x_i) + \frac 1 2 h_i f_t^2(x_i)] + \gamma T_t + \frac 1 2 \lambda \sum_{j=1}^T {w_j^{(t)}}^2 \\ \Omega(f_t) & = \gamma T_t + \frac 1 2 \lambda \sum_{j=1}^T {w_j^{(t)}}^2 \end{align*}$$

  • $f_t$：第t个基学习器
  • $f_t(x_i)$：第t个基学习器对样本$x_i$的取值
  • $gi = \partial{\hat y} l(y_i, \hat y^{t-1})$
  • $hi = \partial^2{\hat y} l(y_i, \hat y^{t-1})$
  • $\Omega(f_t)$：单个基学习器的复杂度罚
  • $T_t$：第t个基学习器参数数量，即$L_0$罚

    • 线性回归基学习器：回归系数数量
    • 回归树基学习器：叶子节点数目

  • $\gamma$：基学习器$L_0$罚系数，模型复杂度惩罚系数
  • $w_j = f_t$：第t个基学习器参数值，即$L_2$罚

    • 线性回归基学习器：回归系数值
    • 回归树基学习器：叶子节点

  • $\lambda$：基学习器$L_2$罚系数，模型贡献惩罚系数
  • $\approx$：由二阶泰勒展开近似

• 对损失函数进行二阶泰勒展开（类似牛顿法）拟合原损失函数， 同时利用一阶、二阶导数求解下个迭代点

• 正则项以控制模型复杂度

  • 降低模型估计误差，避免过拟合
  • $L_2$正则项也控制基学习器的学习量，给后续学习器留下 学习空间

树基学习器

XGBoost Tree：以回归树为基学习器的XGBoost模型

• 模型结构说明

  • 基学习器类型：CART
  • 叶子节点取值作惩罚：各叶子节点取值差别不应过大，否则 说明模型不稳定，稍微改变输入值即导致输出剧烈变化
  • 树复杂度惩罚：叶子结点数量

• XGBoost最终损失（结构风险）有

  $$\begin{align*} R_{srm} & = \sum_{i=1}^N l(y_i, \hat y_i) + \sum_{t=1}^M \Omega(f_t) \end{align*}$$

  • $N, M$：样本量、基学习器数量
  • $\hat y_i$：样本$i$最终预测结果

损失函数

• 以树作基学习器时，第$t$基学习器损失函数为

  $$\begin{align*} obj^{(t)} & = \sum_{i=1}^N l(y_i, \hat y_i^{(t)}) + \Omega(f_t) \\ & \approx \sum_{i=1}^N [l(y_i, \hat y^{(t-1)}) + g_i f_t(x_i) + \frac 1 2 h_i f_t^2(x_i)] + \gamma T_t + \frac 1 2 \lambda \sum_{j=1}^T {w_j^{(t)}}^2 \\ & = \sum_{j=1}^{T_t} [(\sum_{i \in I_j} g_i) w_j^{(t)} + \frac 1 2 (\sum_{i \in I_j} h_i + \lambda) {w_j^{(t)}}^2] + \gamma T_t + \sum_{i=1}^N l(y_i, \hat y^{(t)}) \\ & = \sum_{j=1}^{T_t} [G_i w_j^{(t)} + \frac 1 2 (H_j + \lambda){w_j^{(t)}}^2] + \gamma T_t + \sum_{i=1}^N l(y_i, \hat y^{(t)}) \\ & = \sum_{j=1}^{T_t} [G_i w_j^{(t)} + \frac 1 2 (H_j + \lambda)(w_j^{(t)})^2] + \gamma T_t + \sum_{i=1}^N l(y_i, \hat y^{(t)}) \\ \end{align*}$$

  • $f_t, T_t$：第t棵回归树、树叶子节点
  • $f_t(x_i)$：第t棵回归树对样本$x_i$的预测得分
  • $w_j^{(t)} = f_t(x)$：第t棵树中第j叶子节点预测得分
  • $gi = \partial{\hat y} l(y_i, \hat y^{t-1})$
  • $hi = \partial^2{\hat y} l(y_i, \hat y^{t-1})$
  • $I_j$：第j个叶结点集合
  • $Gj = \sum{i \in I_j} g_i$
  • $Hj = \sum{i \in I_j} h_i$

  • 对回归树，正则项中含有$(w_j^{(t)})^2$作为惩罚，能够 和损失函数二阶导合并，不影响计算

  • 模型复杂度惩罚项惩罚项是针对树的，定义在叶子节点上， 而平方损失是定义在样本上，合并时将其改写

• 第t棵树的整体损失等于其各叶子结点损失加和，且 各叶子结点取值之间独立

  • 则第t棵树各叶子结点使得损失最小的最优取值如下 （$G_j, H_j$是之前所有树的预测得分和的梯度取值，在 当前整棵树的构建中是定值，所以节点包含样本确定后， 最优取值即可确定）

    $$w_j^{(*)} = -\frac {\sum_{i \in I_j} g_i} {\sum_{i \in I_j} h_i + \lambda} = -\frac {G_j} {H_j + \lambda}$$

  • 整棵树结构分数（最小损失）带入即可得

    $$obj^{(t)} = -\frac 1 2 \sum_{j=i}^M \frac {G_j^2} {H_j + \lambda} + \gamma T$$

  • 则在结点分裂为新节点时，树损失变化量为

    $$l_{split} = \frac 1 2 \left [ \frac {(\sum_{i \in I_L} g_i)^2} {\sum_{i \in I_L h_i} + \lambda} + \frac {(\sum_{i \in I_R} g_i)^2} {\sum_{i \in I_R h_i} + \lambda} - \frac {(\sum_{i \in I} g_i)^2} {\sum_{i \in I h_i} + \lambda} \right ] - \gamma$$

    • $I_L, I_R$：结点分裂出的左、右结点

• 则最后应根据树损失变化量确定分裂节点、完成树的分裂，精确 贪心分裂算法如下

  !xgb_exact_greedy_algorithm_for_split_finding

  • 对于连续型特征需遍历所有可能切分点

    • 对特征排序
    • 遍历数据，计算上式给出的梯度统计量、损失变化

  • 不适合数据量非常大、或分布式场景

模型细节

• shrinkage：对新学习的树使用系数$\eta$收缩权重

  • 类似SGD中学习率，降低单棵树的影响，给后续基模型留下 学习空间

• column subsampling：列抽样

  • 效果较传统的行抽样防止过拟合效果更好 （XGB也支持行抽样）
  • 加速计算速度

XGB树分裂算法

• 线性回归作为基学习器时，XGB相当于L0、L2正则化的 Logistic回归、线性回归

近似分割算法

XGB近似分割算法：根据特征分布选取分位数作为候选集，将连续 特征映射至候选点划分桶中，统计其中梯度值、计算最优分割点

!xgb_approximate_algorithm_for_split_finding

• 全局算法：在树构建初始阶段即计算出所有候选分割点，之后 所有构建过程均使用同样候选分割点

  • 每棵树只需计算一次分割点的，步骤少
  • 需要计算更多候选节点才能保证精度

• 局部算法：每次分裂都需要重新计算候选分割点

  • 计算步骤多
  • 总的需要计算的候选节点更少
  • 适合构建较深的树

• 分位点采样算法参见 ml_model/model_enhancement/gradient_boost

Sparsity-aware Split Finding

稀疏特点分裂算法：为每个树节点指定默认分裂方向，缺失值对应 样本归为该方向

• 仅处理非缺失值，算法复杂度和随无缺失数据集大小线性增加， 减少计算量

• 按照升许、降序分别扫描样本两轮，以便将缺失值样本分别归为 两子节点，确定最优默认分裂方向

  

XGB系统设计

Column Block for Parallel Learning

• 建树过程中最耗时的部分为寻找最优切分点，而其中最耗时部分 为数据排序

XGB对每列使用block结构存储数据

• 每列block内数据为CSC压缩格式

  • 特征排序一次，之后所有树构建可以复用（忽略缺失值）
  • 存储样本索引，以便计算样本梯度
  • 方便并行访问、处理所有列，寻找分裂点

• 精确贪心算法：将所有数据（某特征）放在同一block中

  • 可同时对所有叶子分裂点进行计算
  • 一次扫描即可得到所有叶子节点的分割特征点候选者统计 数据

• 近似算法：可以使用多个block、分布式存储数据子集

  • 对local策略提升更大，因为local策略需要多次生成分位点 候选集

Cache-aware Access

• 列block结构通过索引获取数据、计算梯度，会导致非连续内存 访问，降低CPU cache命中率

• 精确贪心算法：使用cache-aware prefetching

  • 对每个线程分配连续缓冲区，读取梯度信息存储其中，再 统计梯度信息
  • 对样本数量较大时更有效

• 近似算法：合理设置block大小为block中最多的样本数

  • 过大容易导致命中率低、过小导致并行化效率不高

Blocks for Out-of-core Computation

• 数据量过大不能全部存放在主存时，将数据划分为多个block 存放在磁盘上，使用独立线程将block读入主存 （这个是指数据划分为块存储、读取，不是列block）

• 磁盘IO提升

  • block compression：将block按列压缩，读取后使用额外 线程解压
  • block sharding：将数据分配至不同磁盘，分别使用线程 读取至内存缓冲区

分位点采样算法—XGB

Quantile Sketch

样本点权重

• 根据已经建立的$t-1$棵树可以得到数据集在已有模型上误差， 采样时根据误差对样本分配权重，对误差大样本采样粒度更大

• 将树按样本点计算损失改写如下

  $$\sum_{i=1}^N \frac 1 2 h_i(f_t(x_i) - \frac {g_i} {h_i})^2 + \Omega(f_t) + constant$$

• 则对各样本，其损失为$f_t(x_i) - \frac {g_i} {h_i}$ 平方和$h_i$乘积，考虑到$f_t(x_i)$为样本点在当前树预测 得分，则可以

  • 将样本点损失视为“二次损失”
  • 将$\frac {g_i} {h_i}$视为样本点“当前标签”
  • 相应将$h_i$视为样本点权重

• 样本权重取值示例

  • 二次损失：$h_i$总为2，相当于不带权
  • 交叉熵损失：$h_i=\hat y(1-\hat y)$为二次函数， 则$\hat y$接近0.5时权重取值大，此时该样本预测值 也确实不准确，符合预期

Rank函数

• 记集合$D={(x_1, h_1), \cdots, (x_n, h_n)}$

• 定义rank函数$r_D: R \rightarrow [0, +\infty)$如下

  $$r_D(z) = \frac 1 {\sum_{(x, h) \in D} h} \sum_{(x, h) \in D, x < z} h$$
  • 即集合$D$中权重分布中给定取值分位数
  • 即取值小于给定值样本加权占比，可视为加权秩

分位点抽样序列

• 分位点抽样即为从集合$D$特征值中抽样，找到升序点序列 $S = {s_1, \cdots, s_l}$满足

  $$|r_D(s_j - r_D(s_{j+1})| < \epsilon$$

  • $\epsilon$：采样率，序列长度$l = 1/\epsilon$
  • $s1 = \min{i} x_i$：特征最小值

  • $sl = \max{i} x_i$：特征最大值

  • 各样本等权分位点抽样已有成熟方法，加权分位点抽样方法 为XGB创新，如下

Weighted Quantile Sketch

Formalization

• 记$Dk={(x{1,k}, h1), \cdots, (x{n,k}, h_n)}$为各 训练样本第$k$维特征、对应二阶导数

  • 考虑到数据点可能具有相同$x, h$取值，$D_k$为可能包含 重复值的multi-set

• 对于多重集$D$，额外定义两个rank函数

  $$\begin{align*} r_D^{-}(y) & = \sum_{(x,h) \in D, x<y} h \\ r_D^{+}(y) & = \sum_{(x,h) \in D, x \leq y} h \end{align*}$$

  定义相应权重函数为

  $$w_D(y) = r_D^{+}(y) - r_D^{-}(y) = \sum_{(x,h) \in D, x=y} h$$

• 多重集$D$上全部权重和定义为

  $$w(D) = \sum_{(x, w) \in D} w$$

Quantile Summary of Weighted Data

• 定义加权数据上的quantile summary为 $Q(D)=(S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$

  • $S$为$D$中特征取值抽样升序序列，其最小、最大值分别 为$D$中特征最小、最大值

  • $\tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D$为定义在 $S$上的函数，满足

    $$\begin{align*} \tilde r_D^{-}(x_i) & \leq r_D^{-}(x_i) \\ \tilde r_D^{+}(x_i) & \leq r_D^{+}(x_i) \\ \tilde w_D(x_i) & \leq w_D(x_i) \\ \tilde r_D^{-}(x_i) + \tilde w_D(x_i) & \leq \tilde r_D^{-}(x_{i+1}) \\ \tilde r_D^{+}(x_i) + \tilde w_D(x_i) & \leq \tilde r_D^{+}(x_{i+1}) \\ \end{align*}$$

• $Q(D)$满足如下条件时，称为 $\epsilon$-approximate quantile summary

  $$\forall y \in D_X, \tilde r_D^{+}(y) - \tilde r_D(y) - \tilde w_D(y) \leq \epsilon w(D)$$
  • 即对任意$y$的秩估计误差在$\epslion$之内

• $\phi-quantile$：秩位于$\phi * N$的元素（一般向下取整）
• $\epsilon-\phi-quantile$：秩位于区间 $[(\phi-\epsilon)N, (\phi+\epsilon)N]$的元素

构建$\epsilon$-Approximate Qunatile Summary

• 初始化：在小规模数据集 $D={(x_1,h_1), \cdots, (x_n,h_n)}$上构建初始 初始quantile summary $Q(D)=(S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$ 满足

  $$\begin{align*} \tilde r_D^{-}(x_i) & \leq r_D^{-}(x_i) \\ \tilde r_D^{+}(x_i) & \leq r_D^{+}(x_i) \\ \tilde w_D(x_i) & \leq w_D(x_i) \end{align*}$$
  • 即初始化$Q(D)$为0-approximate summary

• merge operation：记 $Q(D1)=(S_1, \tilde r{D1}^{+}, \tilde r{D1}^{-}, \tilde w{D1})$、 $Q(D_2)=(S_2, \tilde r{D2}^{+}, \tilde r{D2}^{-}, \tilde w{D_2})$、 $D = D_1 \cup D_2$，则归并后的 $Q(D)=(S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$ 定义为

  $$\begin{align*} S & S_1 \cup S_2 \\ \tilde r_D^{-}(x_i) & = \tilde r_{D_1}^{-}(x_i) + \tilde r_{D_2}^{-}(x_i) \\ \tilde r_D^{+}(x_i) & = \tilde r_{D_1}^{+}(x_i) + \tilde r_{D_2}^{+}(x_i) \\ \tilde w_D(x_i) & = \tilde w_{D_1}(x_i) + \tilde w_{D_2}(x_i) \end{align*}$$

• prune operation：从给定 $Q(D)=(S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$， （其中$S = {x_1, \cdots, x_k }$），构建新的summary $\acute Q(D)=(\acute S, \tilde r_D^{+}, \tilde r_D^{-}, \tilde w_D)$

  • 仅定义域从$S$按如下操作抽取 $\acute S={\acute x1, \cdots, \acute x{b+1}}$

    $$\acute x_i = g(Q, \frac {i-1} b w(D))$$

  • $g(Q, d)$为查询函数，对给定quantile summary $Q$、 秩$d$返回秩最接近$d$的元素

    

名词

Statistic - Frequentist and Bayesian

统计：数学分支，概率论和优化的交集，是数据科学其他分支的理论基础

• 分析方法：验证式分析

  • 统计建模：基于数据构建统计模型，并验证假设
  • 模型预测：运用模型对数据进行预测、分析

• 理论依据：模型驱动，严格的数理支撑

  • 理论体系
    • 概率论、信息论、计算理论、最优化理论、计算机学科等多个领域的交叉学科
    • 并在发展中形成独自的理论体系、方法论
  • 基本假设：同类数据具有一定的统计规律性，可以用概率统计方法加以处理，推断总体特征，如
    • 随机变量描述数据特征
    • 概率分布描述数据统计规律

• 分析对象：以样本为分析对象

  • 从数据出发，提取数据特征、抽象数据模型、发现数据知识，再回到对数据的分析与预测
  • 数据多种多样，包括数字、文字、图像、音视频及其组合
  • 假设数据独立同分布产生
  • 训练数据集往往是人工给出的

Data Mining

• 从现有的信息中提取数据的 pattern、model，即精选最重要、可理解的、有价值的信息

  • 核心目的在于找到 数据变量之间的关系
  • 不是证明假说的方法，而是构建假说的方法
  • 大数据 的发展，传统的数据分析方式无法处理大量“不相关”数据

• 常用技术

  • cluster analysis：聚类分析，揭示数据内在结构
  • classification：判别分析，数据预测
  • regression/decision trees：决策树，模型图形化展示
  • neural networks：神经网络

• 联系

  • 本质上看起来像是 ML、AI 的基础
  • 会使用大量机器学习算法，但是特定的环境、目的和ML不同

• 建模一般策略：类似机器学习

  • 将数据视为高维空间中的点，在高维空间中找到分类面、回归面

Artificial Intelligence

• 研究如何创造智能 agent，并不一定涉及学习、归纳
• 但是大部分情况下，智能 需要从过去的经验中进行归纳，所以 AI 中很大一部分是 ML

Machine Learning

机器学习：从有限观测数据中学习一般性规律，并将规律应用到未观测样本中进行预测（最基本的就是在不确定中得出结论）

• 分析方法：归纳式、探索式分析
• 理论依据：数据驱动，从数据中中学习知识，
• 分析对象：对样本要求低，样本往往不具有随机样本的特征
• 机器学习建模：不假设，通过对高维空间的搜索，找到数据隐藏规律的恰当概括

Shallow Learning

浅层学习：不涉及特征学习，特征抽取依靠人工经验、特征转换方法

• 传统机器学习可以视为浅层学习

• 步骤

  • 数据预处理
  • 特征提取
  • 特征转换
  • 预测

Deep Learning

深度学习：将原始数据特征通过多步特征转换得到更高层次、抽象的特征表示，进一步输入到预测函数得到最终结果

• 主要目的是从数据中自动学习到有效的特征表示

  • 替代人工设计的特征，避免“特征”工程
  • 模型深度不断增加，特征表示能力越强，后续预测更容易

• 相较于浅层学习：需要解决的关键问题是贡献度分配问题

  • 从某种意义上说，深度学习也可以视为强化学习
  • 内部组件不能直接得到监督信息，需要通过整个模型的最终监督信息得到，有延时

• 目前深度学习模型主要是神经网络模型

  • 神经网络可以使用反向传播算法，较好的解决贡献度分配问题

• credit assignment problem：贡献度分配问题，系统中不同组件、参数对最终系统输出结果的贡献、影响

• 深度：原始数据进行非线性特征转换的次数，将深度学习系统看作有向图结构，深度可以看作是从输入节点到输出节点经过最长路径长度

Representing Learning

表示学习：自动学习有效特征、提高最终机器学习模型性能的学习

• 好的学习标准

  • 较强的表示能力：同样大小向量可以表示更多信息
  • 简化后续学习任务：需要包含更高层次语义信息
  • 具有一般性，是任务、领域独立的：期望学到的表示可以容易迁移到其他任务

• 要学习好的高层语义（分布式表示），需要从底层特征开始，经过多步非线程转换得到

  • 深层结构的优点式可以增加特征重用性，指数级增加表示能力
  • 所以表示学习的关键是构建具有一定深度、多层次特征表示

• 传统机器学习中也有关于特征学习的算法，如：主成分分析、线性判别分析、独立成分分析

  • 通过认为设计准则，用于选取有效特征
  • 特征学习、最终预测模型的学习是分开进行的，学习到的特征不一定可以用于提升最终模型分类性能

• Semantic Gap：语义鸿沟，输入数据底层特征和高层语义信息之间不一致性、差异性

表示

• Local Representation：局部表示，离散表示/符号表示

  • 通常可以表示为 one-hot 向量形式
    • 每个特征作为高维局部表示空间中轴上点
  • 不足
    • one-hot 维数很高、不方便扩展
    • 不同特征取值相似度无法衡量

• Distributed Representation：分布式表示

  • 通常可以表示为 低维、稠密 向量
    • 分散在整个低维嵌入空间中中
  • 表示能力强于局部表示
    • 维数低
    • 容易计算相似度

• 神经网络可以用于将高维局部空间 $R^{|V|}$ 映射到非常低维分布式表示空间 $R^d$

End-to-End Learning

端到端学习/训练：学习过程中不进行分模块、分阶段训练，直接优化任务的总体目标

• 不需要给出不同模块、阶段功能，中间过程不需要认为干预
• 训练数据为“输入-输出”对形式，无需提供其他额外信息
• 和深度学习一样，都是要解决“贡献度分配”问题
  • 大部分神经网络模型的深度学习可以看作是端到端学习

Learning Components

Model/Hypothesis/Opimizee/Learner/Learning Algorithm

模型/假说/优化对象/学习器/学习算法：待学习的条件概率分布 $P(Y|X)$、决策函数 $Y=f(X)$

• 概率模型：适合用条件概率分布 $P(Y|X)$ 表示的模型
• 非概率模型：用决策函数 $Y=f(x)$ 表示的模型

• learner：某类模型的总称
• hypothesis：训练好的模型实例，有时也被强调作为学习器应用在某个样本集（如训练集）上得到的结果
• learning algorithm：模型、策略、算法三者的模型总体

Hypothesis Space

假设空间：特征空间（输入空间）到输出空间的映射集合

• 假设空间可以定义为决策函数/条件概率的集合，通常是由参数向量 $\theta$ 决定的函数/条件分布族

  • 假设空间包含所有可能的条件概率分布或决策函数
  • 假设空间的确定意味着学习范围的确定

• 概率模型假设空间可表示为：$F={P|P_{\theta}(Y|X), \theta \in R^n}$

• 非概率模型假设空间可表示为：$F={f|Y=f(x),\Theta \in R^n }$

• 以下大部分情况使用决策函数，同时也可以代表概率分布

Strategy/Goal

策略/目标：从假设空间中，根据 evaluation criterion 选择最优模型，使得其对已知训练数据、未知训练数据在给定评价准则下有最优预测

• 选择合适策略，监督学习问题变为经验风险、结构风险函数 最优化问题

• 在某些学习方法中，最优化问题目标函数也有可能不是风险函数，如：SVM，是和模型紧密相关的损失函数，但逻辑是一样的

Empirical Risk Minimiation

ERM：经验风险最小化策略认为，经验风险最小模型就是最优模型

• 按经验风险最小化求最优模型，等价于求最优化问题

  $$\min_{f \in F} \frac 1 N \sum_{i=1}^N L(y_i, f(x_i))$$

• 样本容量足够大时，经验风险最小化能保证有较好的学习效果，现实中也被广泛采用

Structural Risk Minimization

SRM：结构风险最小化，为防止过拟合提出的策略

• 结构化风险最小化策略认为结构风险最小的模型是最优模型，则求解最优模型等价于求解最优化问题

  $$arg \min_{f \in F} \frac 1 N \sum_{i=1}^N L(y_i, f(x_i)) + \lambda J(f)$$

• 结构风险小需要经验风险与模型复杂度同时小，此时模型往往对训练数据、未知的测试数据都有较好的预测

• 结构化风险最小策略符合 Occam’s Razor 原理

• Occam’s Razor：奥卡姆剃刀原理，在所有可能选择的模型中，能够很好的解释已知数据并且十分简单才是最好的模型

Algorithm/Optimizer

算法/优化器：学习模型（选择、求解最优模型）的具体计算方法 （求解最优化问题）

• 如果最优化问题有显式解析解，比较简单

• 但通常解析解不存在，需要用数值计算方法求解

  • 保证找到全局最优解
  • 高效求解

Supervised Learning

监督学习：学习一个模型，使得模型能够对任意给定输入、输出，做出好的预测

• 从给定的、有限的、用于学习的 train data $T={(x_1,y_1), (x_2,y_2), \cdots, (x_N, y_N)}$ 中学习

• 预测 “未知” test data $T={(x_1,y_1), (x_2,y_2), \cdots, (x_N^{‘}, y_N^{‘})}$

数据

• input space：输入空间 $\chi$，所有输入 $X$ 可能取值的集合
• output space：输出空间 $\gamma$，所有输出 $Y$ 可能取值集合
• feature space：特征空间，表示输入实例 feature vector 存在的空间
  • 特征空间每维对应一个特征
  • 模型实际上是定义在特征空间上的
  • 特征空间是输入空间的象集，有时等于输入空间

学习方法分类

Generative Approach

生成方法：由数据学习联合概率分布 $P(X, Y)$，然后求出条件概率分布 $P(Y|X)$ 作为 generative model

• 方法学习给定输入X产生输出Y的生成关系（联合概率分布）

• generative model：生成模型，由生成方法学习到的模型 $P(Y|X) = \frac {P(X, Y)} {P(X}$

  • 朴素贝叶斯法
  • 隐马尔可夫模型

• 特点

  • 可以还原联合概率分布 $P(X, Y)$
  • 生成方法学习收敛速度快，样本容量增加时，学习到的模型可以快速收敛到真实模型
  • 存在隐变量时，仍可以使用生成方法学习

Discriminative Approach

判别方法：由数据直接学习决策函数 $f(x)$、条件概率分布 $P(Y|X)$ 作为 discriminative model

• 判别方法关心的是对给定输入 $X$，预测输出$Y$

• discriminative model：判别模型

  • KNN
  • 感知机
  • 决策树
  • 逻辑回归
  • 最大熵模型
  • 支持向量机
  • 提升方法
  • 条件随机场

• 特点

  • 直接学习条件概率、决策函数
  • 直面预测，学习准确率更高
  • 可以对数据进行各种程度抽象、定义特征、使用特征，简化学习问题

问题分类

• well-posed problem：好解问题，指问题解应该满足以下条件

  • 解存在
  • 解唯一
  • 解行为随着初值连续变化

• ill-posed problem：病态问题，解不满足以上三个条件

Classification

分类问题：输出变量$Y$为有限个离散变量

• 学习过程：根据已知训练数据集，利用有效学习方法学习分类器 $P(Y|X))$、$Y=F(X)$
• 分类过程：利用学习的分类器对新输入实例进行分类

• 可用学习方法

  • KNN
  • 感知机
  • 朴素贝叶斯
  • 决策树
  • 决策列表
  • 逻辑回归
  • 支持向量机
  • 提升方法
  • 贝叶斯网络
  • 神经网络

• 不存在分类能力弱于随机预测的分类器（结论取反）

Tagging

标注问题：输入、输出 均为变量序列

• 可认为是分类问题的一个推广、更复杂 structure prediction 简单形式
• 学习过程：利用已知训练数据集构建条件概率分布模型 $P(Y^{(1)}, Y^{(2)}, \cdots, Y^{(n)}|X^{(1)}, X^{(2)}, \cdots, X^{(n)})$

  • $X^{(1)}, X^{(2)}, \cdots, X^{(n)}$：每个输入序列
  • $Y^{(1)}, Y^{(2)}, \cdots, Y^{(n)}$：所有可能标记

• 标注过程：按照学习到的条件概率分布，标记新的输入观测序列
• 可用模型
  • 隐马尔可夫模型
  • 条件随机场

Regression

回归问题：输入（自变量）、输出（因变量）均为连续变量

• 回归模型的拟合等价于函数拟合：选择函数曲线很好的拟合已知数据，且很好的预测未知数据
• 学习过程：基于训练数据构架模型（函数）$Y=f(X)$
  • 最常用损失函数是平方损失函数，此时可以使用最小二乘求解
• 预测过程：根据学习到函数模型确定相应输出

Unsupervised Learning

无监督学习：没有给定实现标记过的训练示例，自动对输入的数据进行分类

• 主要目标：预训练一般模型（称识别、编码）网络，供其他任务使用
• 目前为止，有监督模型一般比无监督的预训练模型表现得好
  • 主要原因：有监督模型对数据的 特性编码 更好

问题分类

Clustering 聚类

• Hierarchy Clustering
• K-means
• Mixture Models
• DBSCAN
• OPTICS Algorithm

Anomaly Detection 异常检测

• Local Outlier Factor

Neural Networks 神经网络

• Auto-encoders
• Deep Belief Nets
• Hebbian Learning
• Generative Adversarial Networks
• Self-organizing Map

隐变量学习

• Expectation-maximization Algorithm
• Methods of Moments
• bind signal separation techniques
  • Principal Component analysis
  • Independent Component analysis
  • Non-negative matrix factorization
  • Singular Value Decomposition

Semi-Supervised Learning

半监督学习：利用少量标注数据和大量无标注数据进行学习的方式

• 可以利用大量无标注数据提高监督学习的效果

Reinforcement Learning

强化学习：从与环境交互中不断学习的问题、以及解决这类问题的方法

• 强化学习问题可以描述为：智能体从与环境的交互中不断学习以完成特定目标

• 强化学习的关键问题：贡献度分配问题

  • 每个动作不能直接得到监督信息，需要通过整个模型的最终 监督信息得到，且具有时延性
  • 给出的监督信息也非“正确”策略，而是策略的延迟回报，并通过调整策略以取得最大化期望回报